湖北省蕲春县第一高级中学高中数学必修三课件_2.3变量间的相关关系 (共28张PPT)
文档属性
| 名称 | 湖北省蕲春县第一高级中学高中数学必修三课件_2.3变量间的相关关系 (共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-30 00:00:00 | ||
图片预览







文档简介
课件27张PPT。2.3 变量间的相关关系1.什么是众数、中位数、平均数、方差、
标准差?
2.如何从频率分布直方图中估计众数、中
位数、平均数?
3.方差与标准差的联系与区别是什么?①众数:在一组数据中,出现次数最多的数据(即频率分布最大
值所对应的样本数据)叫这组数据的众数.②中位数:将一组数据按大小依次排列,把处在最中间位置的
一个数据(或中间两个数据的平均数)叫这组数据的中位数.2.众数、中位数、平均数与频率分布直方图的关系 众数是最高矩形的中点所对应的数据,表示样本数据的中心值 .①在频率分布直方图中,中位数左边和右边的直方
图面积相等,由此可以估计中位数的值,但是
有偏差;
②表示样本数据所占频率的等分线 .①平均数等于每个小长方形的面积乘以小长方形底
边中点的横坐标之和;
②平均数是频率分布直方图的中心,是频率分布
直方图的平衡点 .1.什么是众数、中位数、平均数、方差、
标准差?
2.如何从频率分布直方图中估计众数、中
位数、平均数?
3.方差与标准差的联系与区别是什么?方差是标准差s的平方s2,都是用来测量样本数据的
分散程度的特征数.标准差与原数据有相同的单位;
方差的单位是原数据单位的平方 .导入前面我们学习了两个量之间的关系有哪些?相等关系、不等关系;两个量之间的函数关系;思考:在学校里,老师对学生经常这样说:“如果你的数学
成绩好,那么你的物理学习就不会有什么大问题”.按照
这种说法,似乎学生的物理成绩与数学成绩之间存在着
一种相关关系,这种说法有没有根据?2.例题导读
通过对例题的学习,(1)学会如何作散点图;
(2)学会如何用散点图判断两个变量是否相关;
(3)掌握求回归直线方程的方法;
(4)熟悉回归直线方程的实际应用.1.问题导航
(1)什么叫散点图?
(2)相关关系分为哪两种?
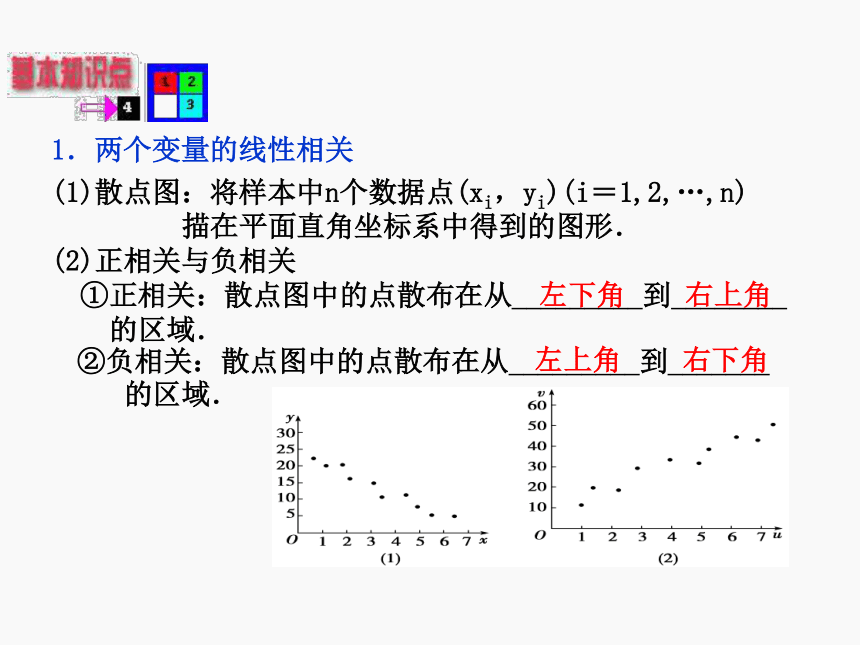
(3)什么叫回归直线?求回归直线的方法及步骤是什么?1.两个变量的线性相关
(1)散点图:将样本中n个数据点(xi,yi)(i=1,2,…,n)
描在平面直角坐标系中得到的图形.
(2)正相关与负相关
①正相关:散点图中的点散布在从_________到________
的区域.左下角右上角左上角右下角 ②负相关:散点图中的点散布在从_________到_______
的区域.2.回归直线的方程
(1)回归直线:如果散点图中点的分布从整体上看大致在
__________附近,我们就称这两个变量之间具有__________
关系,这条直线叫做回归直线.
(2)回归方程:___________对应的方程叫回归直线的方程,
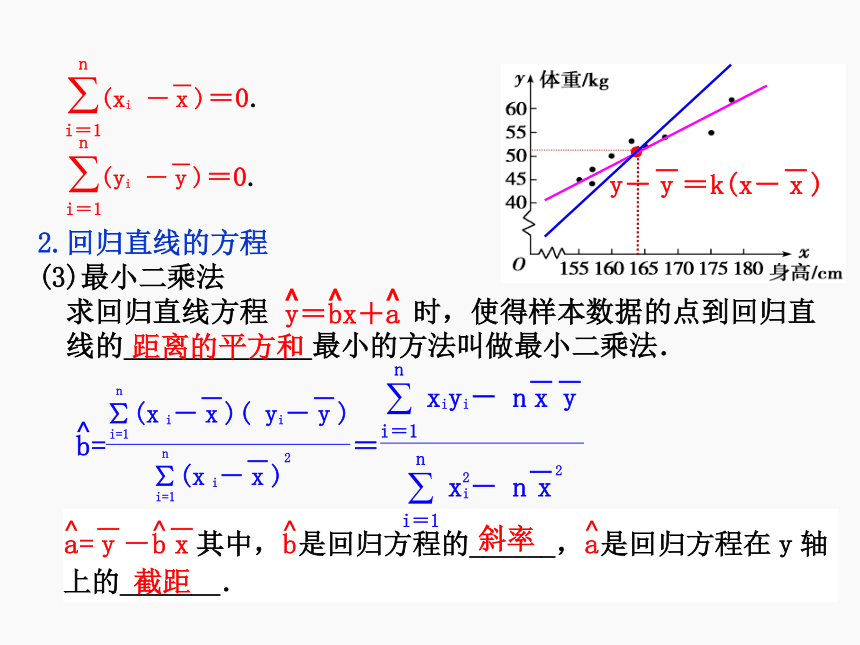
简称回归方程.一条直线回归直线线性相关这组样本点的中心在哪?如何确定回归直线方程呢?·2.回归直线的方程
(3)最小二乘法
求回归直线方程 时,使得样本数据的点到回归直
线的_____________最小的方法叫做最小二乘法.距离的平方和斜率截距·1.两个变量之间的关系与其对应的散点图特征:(3)两个变量间的关系是线性相关时,(2)两个变量间的关系是相关关系时,(1)两个变量间的关系是函数关系时,数据点位于某曲线上.数据点位于某曲线附近.数据点位于某直线附近.2.对回归直线与回归方程的理解
(1)回归方程被样本数据唯一确定,各样本点大致分布在回归直
线附近.对同一个总体,不同的样本数据对应不同的回归直线,
所以回归直线也具有随机性.
(2)对于任意一组样本数据,利用最小二乘法公式都可以求得
“回归方程”,如果这组数据不具有线性相关关系,即不存在
回归直线,那么所得的“回归方程”是没有实际意义的.
因此,对一组样本数据,应先作散点图,在具有线性相关关系
的前提下再求回归方程.例1 (1)下列关系中,属于相关关系的是________.
①人的身高与视力的关系;
②做自由落体运动的物体的质量与落地时间的关系;
③降雪量与交通事故的发生率之间的关系.相关关系的判断③不是相关关系身高与视力无关,不具有函数关系,也不具有相关关系不是函数关系,也不是相关关系自由落体的物体的质量与落地时间无关,不具有相关关系相关关系降雪量越大,交通事故发生率越高,不确定性的关系(2)下表是某地的年降雨量与年平均气温,判断两者是相关关系吗?求回归直线方程有意义吗?解:以x轴为年平均气温,y轴为
年降雨量,可得相应的散点图,
如图所示:因为图中各点并不在一条直线附近,所以两者不具有相关关系,求回归直线方程也是没有意义的.方法归纳
(1)两个变量x和y相关关系的确定方法:(2)判断两个变量x和y之间是否具有线性相关关系,常用的简便
方法就是绘制散点图,如果发现点的分布从整体上看大致在
一条直线附近,那么这两个变量就是线性相关的,注意不要
受个别点的位置的影响.③经验法:②表格、关系式法:①散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断;结合表格或关系式进行判断;借助积累的经验进行分析判断.1.(1)对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);
对变量u,v有观测数据(ui,vi)(i=1,2,…,10),得散点图(2).
由这两个散点图可以判断( )A.变量x与y正相关,u与v正相关 B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关 D.变量x与y负相关,u与v负相关解析:图(1)中的数据y随着x的增大而减小,因此变量x与变量y负相关;图(2)中的数据v随着u的增大而增大,因此u与v正相关.C(2)下面是随机抽取的9名15岁男生的身高、体重表:解:法一:根据经验可知,人的身高和体重之间存在相关关系.法二:观察表格数据可知,人的体重随着身高的增加而增加,
因此人的身高和体重之间存在相关关系.法三:以x轴表示身高,以y轴表
示体重,得到相应的散点图.判断所给的两个变量是否存在相关关系.如图所示:我们会发现,随着身高的增高,体重基本上呈增加趋势.所以体重与身高之间存在相关关系,并且是正相关.(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性
回归方程 ;例2 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录
的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:线性回归方程的建立(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试
根据(2)求出的线性回归方程,预测生产100吨甲产品的生产
能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)3×2.5+4×3+5×4
+6×4.5解 (1)散点图如图:=0.7=3.5-0.7×4.5=0.35∴ 所求的线性回归方程为:=4.5=3.5=66.5=8632+42+52+62·(3)当x=100时,由此可预测生产100吨甲产品的生产能耗比技改前大约降低了19.65吨标准煤.90-70.35=19.65(吨标准煤).y=0.7×100+0.35=70.35(吨标准煤),(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试
根据(2)求出的线性回归方程,预测生产100吨甲产品的生产
能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)变式 如果把本题中的y的值2.5及4.5分别改为2和5,如何求
回归直线方程?∴直线方程为y-2=x-3,可验证这四点共线,解:散点坐标分别为(3,2),(4,3),(5,4),(6,5)方法归纳
求线性回归方程的步骤:(6)写出回归方程.2.测量某地10对父子身高(单位:英寸)如下:如果x与y之间具有线性相关关系,求回归直线方程;如果父亲的身高为78英寸,试估计儿子的身高.解:先将两个变量的数字在表中计算出来,如下表所示:由上表可得:所以当父亲的身高为78英寸时,估计儿子的身高
约为72.213 8英寸.当x=78时,故所求回归直线方程为:≈0.464 6=72.213 8,≈35.975代入公式得:=67.01-0.464 6×66.81.我们常说“吸烟有害健康”,吸烟与健康之间的关系是( )
A.正相关 B.负相关 C.无相关 D.不确定
解析:烟吸得越多,则健康程度越差.B2.线性回归直线是指( )
A.样本少数点在其上的直线
B.样本所有点在其上的直线
C.样本大部分点在其上的直线
D.样本所有点到其距离的平方和最小的直线
解析:由线性回归直线的求法可知线性回归直线是样本所有点到其距离的平方和最小的直线.D单位,y平均增加的单位数x每增加一个2.5得:y=2.5.
标准差?
2.如何从频率分布直方图中估计众数、中
位数、平均数?
3.方差与标准差的联系与区别是什么?①众数:在一组数据中,出现次数最多的数据(即频率分布最大
值所对应的样本数据)叫这组数据的众数.②中位数:将一组数据按大小依次排列,把处在最中间位置的
一个数据(或中间两个数据的平均数)叫这组数据的中位数.2.众数、中位数、平均数与频率分布直方图的关系 众数是最高矩形的中点所对应的数据,表示样本数据的中心值 .①在频率分布直方图中,中位数左边和右边的直方
图面积相等,由此可以估计中位数的值,但是
有偏差;
②表示样本数据所占频率的等分线 .①平均数等于每个小长方形的面积乘以小长方形底
边中点的横坐标之和;
②平均数是频率分布直方图的中心,是频率分布
直方图的平衡点 .1.什么是众数、中位数、平均数、方差、
标准差?
2.如何从频率分布直方图中估计众数、中
位数、平均数?
3.方差与标准差的联系与区别是什么?方差是标准差s的平方s2,都是用来测量样本数据的
分散程度的特征数.标准差与原数据有相同的单位;
方差的单位是原数据单位的平方 .导入前面我们学习了两个量之间的关系有哪些?相等关系、不等关系;两个量之间的函数关系;思考:在学校里,老师对学生经常这样说:“如果你的数学
成绩好,那么你的物理学习就不会有什么大问题”.按照
这种说法,似乎学生的物理成绩与数学成绩之间存在着
一种相关关系,这种说法有没有根据?2.例题导读
通过对例题的学习,(1)学会如何作散点图;
(2)学会如何用散点图判断两个变量是否相关;
(3)掌握求回归直线方程的方法;
(4)熟悉回归直线方程的实际应用.1.问题导航
(1)什么叫散点图?
(2)相关关系分为哪两种?
(3)什么叫回归直线?求回归直线的方法及步骤是什么?1.两个变量的线性相关
(1)散点图:将样本中n个数据点(xi,yi)(i=1,2,…,n)
描在平面直角坐标系中得到的图形.
(2)正相关与负相关
①正相关:散点图中的点散布在从_________到________
的区域.左下角右上角左上角右下角 ②负相关:散点图中的点散布在从_________到_______
的区域.2.回归直线的方程
(1)回归直线:如果散点图中点的分布从整体上看大致在
__________附近,我们就称这两个变量之间具有__________
关系,这条直线叫做回归直线.
(2)回归方程:___________对应的方程叫回归直线的方程,
简称回归方程.一条直线回归直线线性相关这组样本点的中心在哪?如何确定回归直线方程呢?·2.回归直线的方程
(3)最小二乘法
求回归直线方程 时,使得样本数据的点到回归直
线的_____________最小的方法叫做最小二乘法.距离的平方和斜率截距·1.两个变量之间的关系与其对应的散点图特征:(3)两个变量间的关系是线性相关时,(2)两个变量间的关系是相关关系时,(1)两个变量间的关系是函数关系时,数据点位于某曲线上.数据点位于某曲线附近.数据点位于某直线附近.2.对回归直线与回归方程的理解
(1)回归方程被样本数据唯一确定,各样本点大致分布在回归直
线附近.对同一个总体,不同的样本数据对应不同的回归直线,
所以回归直线也具有随机性.
(2)对于任意一组样本数据,利用最小二乘法公式都可以求得
“回归方程”,如果这组数据不具有线性相关关系,即不存在
回归直线,那么所得的“回归方程”是没有实际意义的.
因此,对一组样本数据,应先作散点图,在具有线性相关关系
的前提下再求回归方程.例1 (1)下列关系中,属于相关关系的是________.
①人的身高与视力的关系;
②做自由落体运动的物体的质量与落地时间的关系;
③降雪量与交通事故的发生率之间的关系.相关关系的判断③不是相关关系身高与视力无关,不具有函数关系,也不具有相关关系不是函数关系,也不是相关关系自由落体的物体的质量与落地时间无关,不具有相关关系相关关系降雪量越大,交通事故发生率越高,不确定性的关系(2)下表是某地的年降雨量与年平均气温,判断两者是相关关系吗?求回归直线方程有意义吗?解:以x轴为年平均气温,y轴为
年降雨量,可得相应的散点图,
如图所示:因为图中各点并不在一条直线附近,所以两者不具有相关关系,求回归直线方程也是没有意义的.方法归纳
(1)两个变量x和y相关关系的确定方法:(2)判断两个变量x和y之间是否具有线性相关关系,常用的简便
方法就是绘制散点图,如果发现点的分布从整体上看大致在
一条直线附近,那么这两个变量就是线性相关的,注意不要
受个别点的位置的影响.③经验法:②表格、关系式法:①散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断;结合表格或关系式进行判断;借助积累的经验进行分析判断.1.(1)对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);
对变量u,v有观测数据(ui,vi)(i=1,2,…,10),得散点图(2).
由这两个散点图可以判断( )A.变量x与y正相关,u与v正相关 B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关 D.变量x与y负相关,u与v负相关解析:图(1)中的数据y随着x的增大而减小,因此变量x与变量y负相关;图(2)中的数据v随着u的增大而增大,因此u与v正相关.C(2)下面是随机抽取的9名15岁男生的身高、体重表:解:法一:根据经验可知,人的身高和体重之间存在相关关系.法二:观察表格数据可知,人的体重随着身高的增加而增加,
因此人的身高和体重之间存在相关关系.法三:以x轴表示身高,以y轴表
示体重,得到相应的散点图.判断所给的两个变量是否存在相关关系.如图所示:我们会发现,随着身高的增高,体重基本上呈增加趋势.所以体重与身高之间存在相关关系,并且是正相关.(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性
回归方程 ;例2 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录
的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:线性回归方程的建立(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试
根据(2)求出的线性回归方程,预测生产100吨甲产品的生产
能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)3×2.5+4×3+5×4
+6×4.5解 (1)散点图如图:=0.7=3.5-0.7×4.5=0.35∴ 所求的线性回归方程为:=4.5=3.5=66.5=8632+42+52+62·(3)当x=100时,由此可预测生产100吨甲产品的生产能耗比技改前大约降低了19.65吨标准煤.90-70.35=19.65(吨标准煤).y=0.7×100+0.35=70.35(吨标准煤),(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试
根据(2)求出的线性回归方程,预测生产100吨甲产品的生产
能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)变式 如果把本题中的y的值2.5及4.5分别改为2和5,如何求
回归直线方程?∴直线方程为y-2=x-3,可验证这四点共线,解:散点坐标分别为(3,2),(4,3),(5,4),(6,5)方法归纳
求线性回归方程的步骤:(6)写出回归方程.2.测量某地10对父子身高(单位:英寸)如下:如果x与y之间具有线性相关关系,求回归直线方程;如果父亲的身高为78英寸,试估计儿子的身高.解:先将两个变量的数字在表中计算出来,如下表所示:由上表可得:所以当父亲的身高为78英寸时,估计儿子的身高
约为72.213 8英寸.当x=78时,故所求回归直线方程为:≈0.464 6=72.213 8,≈35.975代入公式得:=67.01-0.464 6×66.81.我们常说“吸烟有害健康”,吸烟与健康之间的关系是( )
A.正相关 B.负相关 C.无相关 D.不确定
解析:烟吸得越多,则健康程度越差.B2.线性回归直线是指( )
A.样本少数点在其上的直线
B.样本所有点在其上的直线
C.样本大部分点在其上的直线
D.样本所有点到其距离的平方和最小的直线
解析:由线性回归直线的求法可知线性回归直线是样本所有点到其距离的平方和最小的直线.D单位,y平均增加的单位数x每增加一个2.5得:y=2.5.
