运用点差法巧解圆锥曲线的中点弦问题
文档属性
| 名称 | 运用点差法巧解圆锥曲线的中点弦问题 |  | |
| 格式 | zip | ||
| 文件大小 | 488.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-30 21:33:00 | ||
图片预览





文档简介
课件15张PPT。运用点差法巧解圆锥曲线的
中点弦问题高中数学教师欧阳文丰制作 导 言
圆锥曲线综合题是每年高考必考的题目,这些题目的解法灵活多变,其中涉及圆锥曲线中点弦的有关问题,我们称之为圆锥曲线的中点弦问题。用点差法求解此类问题,具有构思精巧,简便易行的优点。
若设直线与圆锥曲线的交点(弦的端点)坐标为、,将这两点代入圆锥曲线的方程并对所得两式作差,得到一个与弦的中点和斜率有关的式子,可以大大减少运算量。我们称这种代点作差的方法为“点差法”。
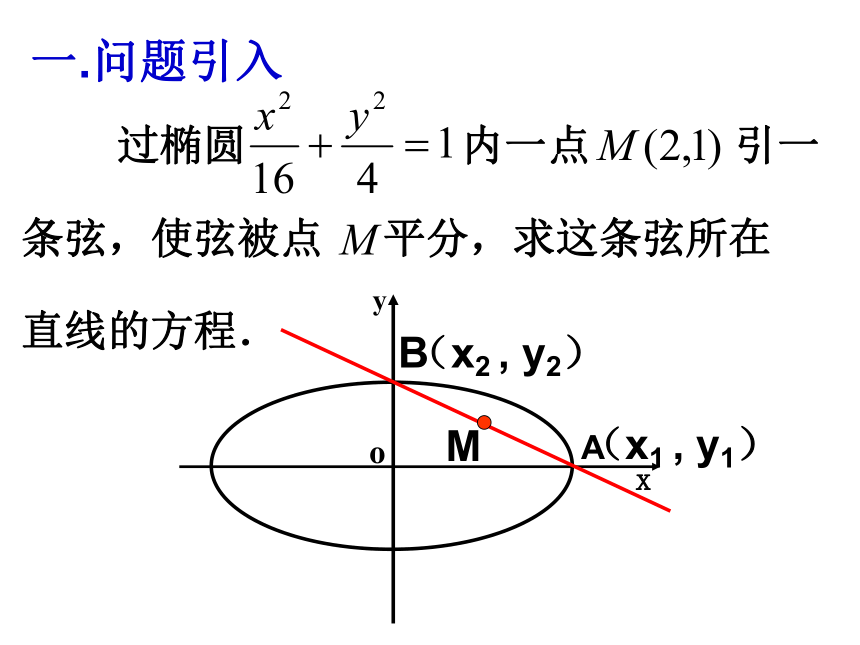
A(x2 , y2)M(x1 , y1)B一.问题引入例1:已知椭圆 过点P(2,1)引一弦,使弦在这点被平分,求此弦所在直线的方程.解法一:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造二、例题讲解例1:已知椭圆 过点P(2,1)引一弦,使弦在这点被
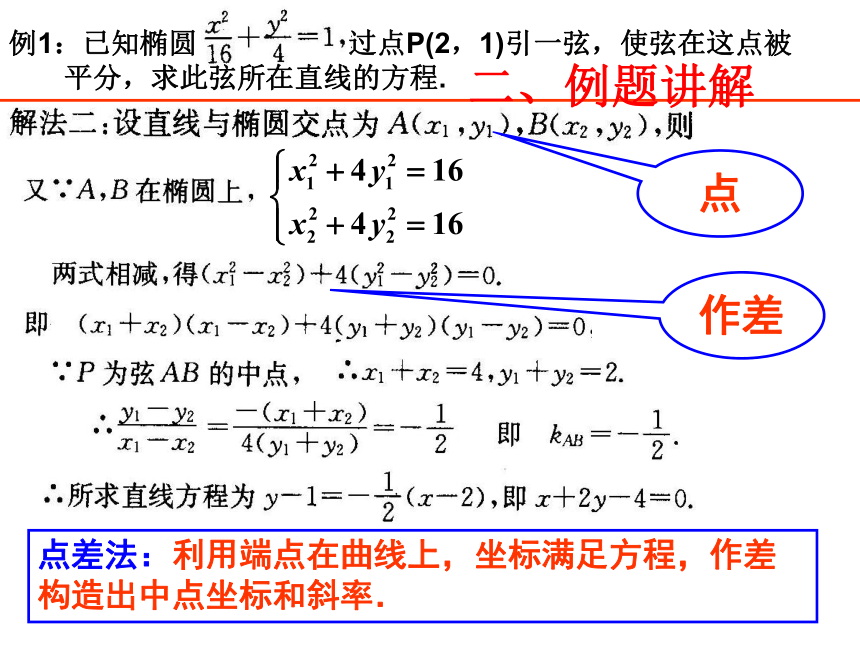
平分,求此弦所在直线的方程.点差法:利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率.点作差二、例题讲解小结:弦中点、弦斜率问题的两种处理方法 1.联立方程组,消去一个未知数,利用韦达定理解决. 2.点差法:设弦的两端点坐标,代入曲线方程相减后分解
因式,便可与弦所在直线的斜率及弦的中点联系起来.点差法例2二、例题讲解二、例题讲解例3、已知椭圆,求它的斜率为3的弦中点的轨迹方程。 解:设弦端点、,弦的中点,则
,
又 ,两式相减得即,即 ,即由,得弦中点的轨迹方程为:二、例题讲解例4 已知椭圆的一条准线方程是,有一条倾斜角为的直线交椭圆于A、B两点,若AB的中点为,则求椭圆的方程。二、例题讲解解 设,则,且,(1),(2)
得:,,
,(3)
,,(4),(5)由(3),(4),(5)可得,
所求椭圆方程为.二、例题讲解注:凡关于中点弦和弦中点的问题,可采用点差法求解。三、变式练习三、变式练习2.弦中点问题的两种处理方法 课堂小结 (1)联立方程组,消去一个未知数,利用韦达定理; (2)设两端点坐标,代入曲线方程相减可求出弦的斜率和弦的中点坐标(点差法)。1、利用点差法求解圆锥曲线中点弦问题,方法简捷明快,结构精巧,很好地体现了数学美,而且应用特征明显,是训练思维、熏陶数学情感的一个很好的材料,利于培养学生的解题能力和解题兴趣。作业:抛物线y=x2-2x+2与直线y=mx交于P1、P2两点 (1)求线段P1P2中点Q的轨迹方程; (2)0≤x≤2求线段P1P2中点Q的最高点和最低点坐标。
中点弦问题高中数学教师欧阳文丰制作 导 言
圆锥曲线综合题是每年高考必考的题目,这些题目的解法灵活多变,其中涉及圆锥曲线中点弦的有关问题,我们称之为圆锥曲线的中点弦问题。用点差法求解此类问题,具有构思精巧,简便易行的优点。
若设直线与圆锥曲线的交点(弦的端点)坐标为、,将这两点代入圆锥曲线的方程并对所得两式作差,得到一个与弦的中点和斜率有关的式子,可以大大减少运算量。我们称这种代点作差的方法为“点差法”。
A(x2 , y2)M(x1 , y1)B一.问题引入例1:已知椭圆 过点P(2,1)引一弦,使弦在这点被平分,求此弦所在直线的方程.解法一:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造二、例题讲解例1:已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.点差法:利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率.点作差二、例题讲解小结:弦中点、弦斜率问题的两种处理方法 1.联立方程组,消去一个未知数,利用韦达定理解决. 2.点差法:设弦的两端点坐标,代入曲线方程相减后分解
因式,便可与弦所在直线的斜率及弦的中点联系起来.点差法例2二、例题讲解二、例题讲解例3、已知椭圆,求它的斜率为3的弦中点的轨迹方程。 解:设弦端点、,弦的中点,则
,
又 ,两式相减得即,即 ,即由,得弦中点的轨迹方程为:二、例题讲解例4 已知椭圆的一条准线方程是,有一条倾斜角为的直线交椭圆于A、B两点,若AB的中点为,则求椭圆的方程。二、例题讲解解 设,则,且,(1),(2)
得:,,
,(3)
,,(4),(5)由(3),(4),(5)可得,
所求椭圆方程为.二、例题讲解注:凡关于中点弦和弦中点的问题,可采用点差法求解。三、变式练习三、变式练习2.弦中点问题的两种处理方法 课堂小结 (1)联立方程组,消去一个未知数,利用韦达定理; (2)设两端点坐标,代入曲线方程相减可求出弦的斜率和弦的中点坐标(点差法)。1、利用点差法求解圆锥曲线中点弦问题,方法简捷明快,结构精巧,很好地体现了数学美,而且应用特征明显,是训练思维、熏陶数学情感的一个很好的材料,利于培养学生的解题能力和解题兴趣。作业:抛物线y=x2-2x+2与直线y=mx交于P1、P2两点 (1)求线段P1P2中点Q的轨迹方程; (2)0≤x≤2求线段P1P2中点Q的最高点和最低点坐标。
