12.1-12.2 全等三角形的判定与性质培优提高试题
文档属性
| 名称 | 12.1-12.2 全等三角形的判定与性质培优提高试题 |  | |
| 格式 | zip | ||
| 文件大小 | 785.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-12 11:20:59 | ||
图片预览




文档简介
登陆21世纪教育 助您教考全无忧
12.1-2 全等三角形的判定与性质培优提高
本卷满分120分 总共三大题 时间120分钟
一.选择题(每小题3分 共30分)
1.下列各组的两个图形属于全等图形的是 ( )
A. B. C. D.
2.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第1块 B.第2块 C.第3块 D.第4块
3.如图,若△ABC≌△DEF,∠A=45°,∠F=35°,则∠E等于( )
A.35° B.45° C.60° D.100°
4.下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )
A.①②③④ B.①③④ C.①②④ D.②③④
5.如图,已知AC=A′C′,∠C=∠C′,若△ABC≌△A′B′C′,还需要添加( )
A.BC=B′C′ B.∠B=∠B′ C.∠A=∠A′ D.以上都可以
6.下列各组条件,不能判定△ABC≌△A′B′C′的一组是( )
A.AC=A′C′∠B=∠B BC=B′C B.∠A=∠A′∠B=∠B′AC=A′C
C.AB=A′B′∠A=∠A′AC=A′C′ D.AB=A′B′AC=A′C′BC=B′C
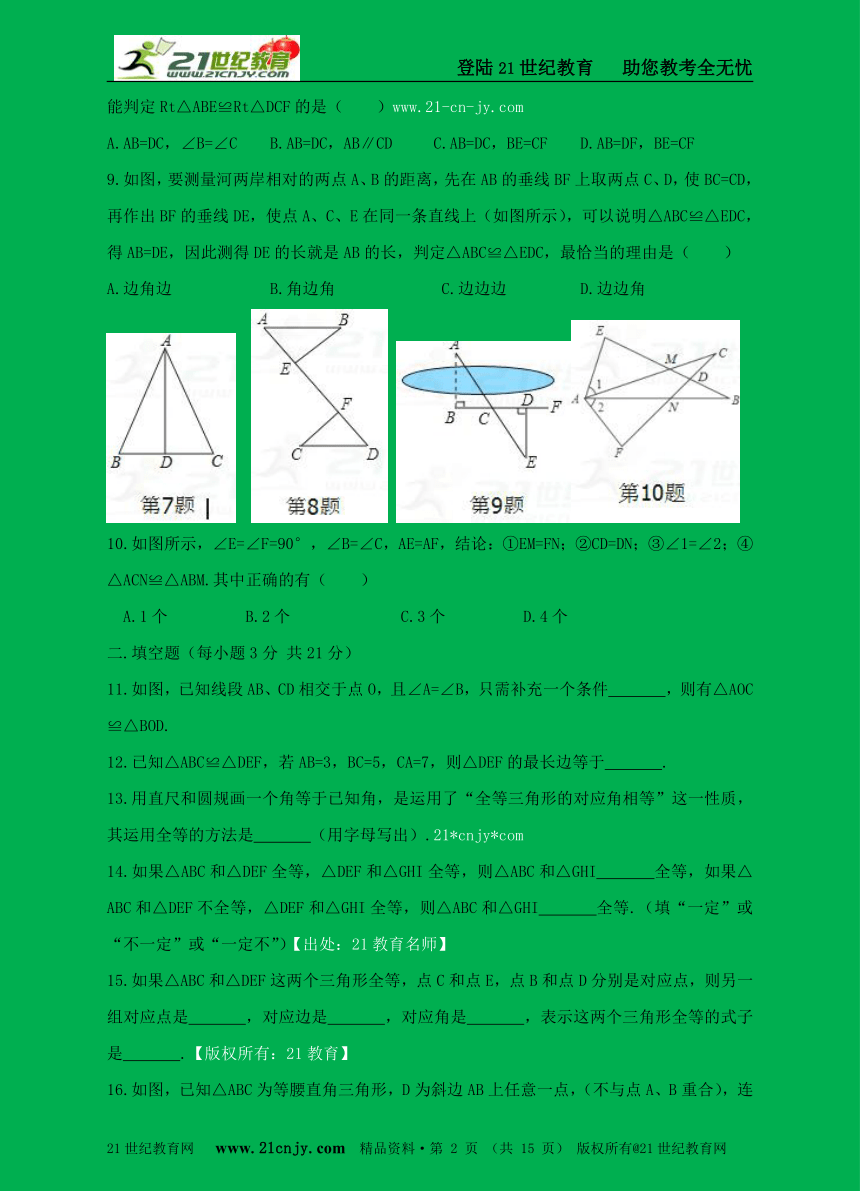
7.如图,AD⊥BC,D是BC的中点,那么下列结论错误的是( )
A.△ABD≌△ACD B.∠B=∠C
C.△ABC是等腰三角形 D.△ABC是等边三角形
8.如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )www.21-cn-jy.com
A.AB=DC,∠B=∠C B.AB=DC,AB∥CD C.AB=DC,BE=CF D.AB=DF,BE=CF
9.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.边角边 B.角边角 C.边边边 D.边边角
10.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每小题3分 共21分)
11.如图,已知线段AB、CD相交于点O,且∠A=∠B,只需补充一个条件 ,则有△AOC≌△BOD.
12.已知△ABC≌△DEF,若AB=3,BC=5,CA=7,则△DEF的最长边等于 .
13.用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是 (用字母写出).21*cnjy*com
14.如果△ABC和△DEF全等,△DEF和△GHI全等,则△ABC和△GHI 全等,如果△ABC和△DEF不全等,△DEF和△GHI全等,则△ABC和△GHI 全等.(填“一定”或“不一定”或“一定不”)【出处:21教育名师】
15.如果△ABC和△DEF这两个三角形全等,点C和点E,点B和点D分别是对应点,则另一组对应点是 ,对应边是 ,对应角是 ,表示这两个三角形全等的式子是 .【版权所有:21教育】
16.如图,已知△ABC为等腰直角三角形,D为斜边AB上任意一点,(不与点A、B重合),连接CD,作EC⊥DC,且EC=DC,连接AE,则∠EAC为 度.21教育名师原创作品
17.如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在AE两侧,BD⊥AE于D,AE⊥CE于E,DE=4cm,CE=2cm,则BD= cm.21*cnjy*com
三.解答题(18-19每题4分,20-24每题6分 25-27每题7分 28题9分)
18.如图,△ABC的顶点A、B、C都在小正方形的顶点上,像这样的三角形叫做格点三角形.若下列每个小正方形的边长均为1,试在下面5×5的方格纸上按要求解决下列问题:
(1)填空:AB= ,S△ABC= .
(2)画格点三角形,使所画的三角形与△ABC全等且只有一个公共顶点C(至少画出两个).
19.如图,已知AB∥DE,AB⊥FC,垂足为点B,AC=DF,FE=CB.求证:∠C=∠F.
20.为了测量一池塘的两端A,B之间的距离,同学们想出了如下的两种方案:
①如图1,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,BC至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长;
②如图2,过点B作AB的垂线BF,在BF上取C,D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即是AB的距离.
问: (1)方案①是否可行? ,理由是 ;
(2)方案②是否可行? ,理由是 ;
(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要 就可以了,请把小明所说的条件补上.
21.如图,一个特大型设备人字梁,工人师傅要检查人字梁的AB和AC是否相等,但是他直接测量不方便,身边只有一个刻度尺(长度远远不够).它是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长a米,FG的长b米,如果a=b,则说明AB和AC是相等的,他的这种做法合理吗?为什么?
22.同学们知道:只有两边和其中一边的对角对应相等的两个三角形不一定全等.在△ABC中和△ADC中,AB=AD,∠BCA=∠DCA,当∠BCA分别为“直角、钝角、锐角”时,探究这两个三角形会不会全等.21世纪教育网版权所有
(1)填空:如图A,当∠BCA是直角时:
∵△ABC和△ADC,AB=AD,AC=AC,∠BCA=∠DCA=90°.
∴△ABC≌△ADC .(从SAS、ASA、AAS、SSS、HL中选取一项作为理由)
(2)如图B,当∠BCA是钝角时,求证:△ABC≌△ADC.(提示:过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F)
(3)当∠BCA是锐角时,△ABC和∠ADC不一定全等.
例如:如图C,在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.
当∠BCA满足什么条件时,可得△ABC≌△ADC?请直接写出这个条件: .
23.在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.21cnjy.com
24.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
25.已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1,求证:AE=BD;
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
26.在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示).
(2)用等式表示线段MB与PQ之间的数量关系,并证明.
27.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)写出图中一对全等的三角形,并写出它们的所有对应角;
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)21教育网
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律. 21·世纪*教育网
28.已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.【来源:21cnj*y.co*m】
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
参考答案
12: 7 解:∵△ABC≌△DEF,且最长边为CA=7,∴△DEF的最长边等于7,
13: SSS 解:补充条件:AC=BD,
∵在△AOC和△DOB中,∴△AOC≌△BOD(AAS).
14:一定 ;一定不解:根据全等三角形的传递性,△ABC和△GHI一定全等,三者有一对不重合则△ABC和△GHI一定不重合,则二者不全等.
15:点A和点F;AC和EF;∠A=∠F.△ABC≌△DEF
16:45. 解:∵△ABC是等腰直角三角形,∠ACB=90°,∴AC=CB.
∵∠ACB=∠DCE=90°,
∴∠ACE=90°﹣∠ACD=∠DCB.
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS).
∴ ∠B=∠EAC(全等三角形的对应角相等).
∵∠B=45°,∴∠EAC=45°.
17: 6 解:∵BD⊥AE于D,AE⊥CE于E,∠BAC=90°
∠BDA=∠AEC=90°,∠EAC+∠ACE=90°,∠EAC+∠BAD=90°
∴∠BAD=∠ACE
在△ABD与△CAE中
∴△ABD≌△CAE(AAS)∴AD=CE,BD=AE
∵DE=4cm,CE=2cm∴AE=AD+DE=CE+DE=6cm ∴BD=6cm.
三、解答题
20.(1)方案①是否可行? 可行 ,理由是 SAS可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED ;21·cn·jy·com
(2)方案②是否可行? 可行 ,理由是 ASA可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED ;
(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要 AB∥DE 就可以了,请把小明所说的条件补上.
21.解:合理,理由:
在△BDE和△CFG中,
,
∴△BDE≌△CFG(SSS),
∴∠B=∠C,
∴AB=AC.
22.解:(1)HL;
(2)过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F,
∵∠BCA=∠DCA,∴∠ACE=∠ACF,
在△AEC和△AFC中,
,
∴△AEC≌△AFC,(AAS)∴AE=AF,
在RT△ADE和RT△ABF中,
,
∴RT△ADE≌RT△ABF(HL),∴∠B=∠D,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(AAS);
(3)∠BCA≥∠BAC,
理由:在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.【来源:21·世纪·教育·网】
不全等原因是因为∠BAE可以是锐角也可以是钝角,
添加条件∠BCA≥∠BAC,此时∠BAC只能是锐角,
故此时用“SAS”方法即可判定△ABC≌△ADC.
23.解:在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE(全等三角形的对应角相等),
∴BF=CE(全等三角形的对应边相等),
24.(1)证明:
∵AC=AD,
∴∠ACD=∠ADC,
又∵∠BCD=∠EDC=90°,
∴∠ACB=∠ADE,
在△ABC和△AED中,
,
∴△ABC≌△AED(SAS);
(2)解:当∠B=140°时,∠E=140°,
又∵∠BCD=∠EDC=90°,
∴五边形ABCDE中,∠BAE=540°﹣140°×2﹣90°×2=80°.
25.解:(1)∵△ACB和△DCE都是等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△ACE与△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD,
(2)∵AC=DC,
∴AC=CD=EC=CB,
△ACB≌△DCE(SAS);
由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC
∴∠DOM=90°,
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BCN(ASA),
∴CM=CN,
∴DM=AN,
△AON≌△DOM(AAS),
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL)
26.解:(1)∠AMQ=45°+α;理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°﹣α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α;
(2)PQ=MB;理由如下:
连接AQ,作ME⊥QB,如图所示:
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
即PQ=MB.
27.解:(1)△EAD≌△EA'D,其中∠EAD=∠EA'D,∠AED=∠A'ED,
∠ADE=∠A'DE;
(2)∠1=180°﹣2x,∠2=180°﹣2y;
(3)∵∠1+∠2=360°﹣2(x+y)=360°﹣2(180°﹣∠A)=2∠A.
规律为:∠1+∠2=2∠A.
28.证明:(1)①如图1,
∵AB⊥AD,AE⊥AC,
∴∠BAD=90°,∠CAE=90°,
∴∠1=∠2,
在△ABC和△ADE中,
∵
∴△ABC≌△ADE(SAS);
②如图1,
∵△ABC≌△ADE,
∴∠AEC=∠3,
在Rt△ACE中,∠ACE+∠AEC=90°,
∴∠BCE=90°,
∵AH⊥CD,AE=AC,
∴CH=HE,
∵∠AHE=∠BCE=90°,
∴BC∥FH,
∴==1,
∴BF=EF;
(2)结论仍然成立,理由是:
如图2所示,过E作MN∥AH,交BA、CD延长线于M、N,
∵∠CAE=90°,∠BAD=90°,
∴∠1+∠2=90°,∠1+∠CAD=90°,
∴∠2=∠CAD,
∵MN∥AH,
∴∠3=∠HAE,
∵∠ACH+∠CAH=90°,∠CAH+∠HAE=90°,
∴∠ACH=∠HAE,
∴∠3=∠ACH,
在△MAE和△DAC中,
∵
∴△MAE≌△DAC(ASA),
∴AM=AD,∵AB=AD,∴AB=AM,∵AF∥ME,∴==1,∴BF=EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 5 页 (共 15 页) 版权所有@21世纪教育网
12.1-2 全等三角形的判定与性质培优提高
本卷满分120分 总共三大题 时间120分钟
一.选择题(每小题3分 共30分)
1.下列各组的两个图形属于全等图形的是 ( )
A. B. C. D.
2.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第1块 B.第2块 C.第3块 D.第4块
3.如图,若△ABC≌△DEF,∠A=45°,∠F=35°,则∠E等于( )
A.35° B.45° C.60° D.100°
4.下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )
A.①②③④ B.①③④ C.①②④ D.②③④
5.如图,已知AC=A′C′,∠C=∠C′,若△ABC≌△A′B′C′,还需要添加( )
A.BC=B′C′ B.∠B=∠B′ C.∠A=∠A′ D.以上都可以
6.下列各组条件,不能判定△ABC≌△A′B′C′的一组是( )
A.AC=A′C′∠B=∠B BC=B′C B.∠A=∠A′∠B=∠B′AC=A′C
C.AB=A′B′∠A=∠A′AC=A′C′ D.AB=A′B′AC=A′C′BC=B′C
7.如图,AD⊥BC,D是BC的中点,那么下列结论错误的是( )
A.△ABD≌△ACD B.∠B=∠C
C.△ABC是等腰三角形 D.△ABC是等边三角形
8.如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )www.21-cn-jy.com
A.AB=DC,∠B=∠C B.AB=DC,AB∥CD C.AB=DC,BE=CF D.AB=DF,BE=CF
9.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.边角边 B.角边角 C.边边边 D.边边角
10.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每小题3分 共21分)
11.如图,已知线段AB、CD相交于点O,且∠A=∠B,只需补充一个条件 ,则有△AOC≌△BOD.
12.已知△ABC≌△DEF,若AB=3,BC=5,CA=7,则△DEF的最长边等于 .
13.用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是 (用字母写出).21*cnjy*com
14.如果△ABC和△DEF全等,△DEF和△GHI全等,则△ABC和△GHI 全等,如果△ABC和△DEF不全等,△DEF和△GHI全等,则△ABC和△GHI 全等.(填“一定”或“不一定”或“一定不”)【出处:21教育名师】
15.如果△ABC和△DEF这两个三角形全等,点C和点E,点B和点D分别是对应点,则另一组对应点是 ,对应边是 ,对应角是 ,表示这两个三角形全等的式子是 .【版权所有:21教育】
16.如图,已知△ABC为等腰直角三角形,D为斜边AB上任意一点,(不与点A、B重合),连接CD,作EC⊥DC,且EC=DC,连接AE,则∠EAC为 度.21教育名师原创作品
17.如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在AE两侧,BD⊥AE于D,AE⊥CE于E,DE=4cm,CE=2cm,则BD= cm.21*cnjy*com
三.解答题(18-19每题4分,20-24每题6分 25-27每题7分 28题9分)
18.如图,△ABC的顶点A、B、C都在小正方形的顶点上,像这样的三角形叫做格点三角形.若下列每个小正方形的边长均为1,试在下面5×5的方格纸上按要求解决下列问题:
(1)填空:AB= ,S△ABC= .
(2)画格点三角形,使所画的三角形与△ABC全等且只有一个公共顶点C(至少画出两个).
19.如图,已知AB∥DE,AB⊥FC,垂足为点B,AC=DF,FE=CB.求证:∠C=∠F.
20.为了测量一池塘的两端A,B之间的距离,同学们想出了如下的两种方案:
①如图1,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,BC至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长;
②如图2,过点B作AB的垂线BF,在BF上取C,D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即是AB的距离.
问: (1)方案①是否可行? ,理由是 ;
(2)方案②是否可行? ,理由是 ;
(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要 就可以了,请把小明所说的条件补上.
21.如图,一个特大型设备人字梁,工人师傅要检查人字梁的AB和AC是否相等,但是他直接测量不方便,身边只有一个刻度尺(长度远远不够).它是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长a米,FG的长b米,如果a=b,则说明AB和AC是相等的,他的这种做法合理吗?为什么?
22.同学们知道:只有两边和其中一边的对角对应相等的两个三角形不一定全等.在△ABC中和△ADC中,AB=AD,∠BCA=∠DCA,当∠BCA分别为“直角、钝角、锐角”时,探究这两个三角形会不会全等.21世纪教育网版权所有
(1)填空:如图A,当∠BCA是直角时:
∵△ABC和△ADC,AB=AD,AC=AC,∠BCA=∠DCA=90°.
∴△ABC≌△ADC .(从SAS、ASA、AAS、SSS、HL中选取一项作为理由)
(2)如图B,当∠BCA是钝角时,求证:△ABC≌△ADC.(提示:过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F)
(3)当∠BCA是锐角时,△ABC和∠ADC不一定全等.
例如:如图C,在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.
当∠BCA满足什么条件时,可得△ABC≌△ADC?请直接写出这个条件: .
23.在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.21cnjy.com
24.如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
25.已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1,求证:AE=BD;
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
26.在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示).
(2)用等式表示线段MB与PQ之间的数量关系,并证明.
27.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)写出图中一对全等的三角形,并写出它们的所有对应角;
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)21教育网
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律. 21·世纪*教育网
28.已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.【来源:21cnj*y.co*m】
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
参考答案
12: 7 解:∵△ABC≌△DEF,且最长边为CA=7,∴△DEF的最长边等于7,
13: SSS 解:补充条件:AC=BD,
∵在△AOC和△DOB中,∴△AOC≌△BOD(AAS).
14:一定 ;一定不解:根据全等三角形的传递性,△ABC和△GHI一定全等,三者有一对不重合则△ABC和△GHI一定不重合,则二者不全等.
15:点A和点F;AC和EF;∠A=∠F.△ABC≌△DEF
16:45. 解:∵△ABC是等腰直角三角形,∠ACB=90°,∴AC=CB.
∵∠ACB=∠DCE=90°,
∴∠ACE=90°﹣∠ACD=∠DCB.
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS).
∴ ∠B=∠EAC(全等三角形的对应角相等).
∵∠B=45°,∴∠EAC=45°.
17: 6 解:∵BD⊥AE于D,AE⊥CE于E,∠BAC=90°
∠BDA=∠AEC=90°,∠EAC+∠ACE=90°,∠EAC+∠BAD=90°
∴∠BAD=∠ACE
在△ABD与△CAE中
∴△ABD≌△CAE(AAS)∴AD=CE,BD=AE
∵DE=4cm,CE=2cm∴AE=AD+DE=CE+DE=6cm ∴BD=6cm.
三、解答题
20.(1)方案①是否可行? 可行 ,理由是 SAS可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED ;21·cn·jy·com
(2)方案②是否可行? 可行 ,理由是 ASA可证明△ACB≌△DCE,再根据全等三角形的性质可得AB=ED ;
(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要 AB∥DE 就可以了,请把小明所说的条件补上.
21.解:合理,理由:
在△BDE和△CFG中,
,
∴△BDE≌△CFG(SSS),
∴∠B=∠C,
∴AB=AC.
22.解:(1)HL;
(2)过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F,
∵∠BCA=∠DCA,∴∠ACE=∠ACF,
在△AEC和△AFC中,
,
∴△AEC≌△AFC,(AAS)∴AE=AF,
在RT△ADE和RT△ABF中,
,
∴RT△ADE≌RT△ABF(HL),∴∠B=∠D,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(AAS);
(3)∠BCA≥∠BAC,
理由:在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.【来源:21·世纪·教育·网】
不全等原因是因为∠BAE可以是锐角也可以是钝角,
添加条件∠BCA≥∠BAC,此时∠BAC只能是锐角,
故此时用“SAS”方法即可判定△ABC≌△ADC.
23.解:在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE(全等三角形的对应角相等),
∴BF=CE(全等三角形的对应边相等),
24.(1)证明:
∵AC=AD,
∴∠ACD=∠ADC,
又∵∠BCD=∠EDC=90°,
∴∠ACB=∠ADE,
在△ABC和△AED中,
,
∴△ABC≌△AED(SAS);
(2)解:当∠B=140°时,∠E=140°,
又∵∠BCD=∠EDC=90°,
∴五边形ABCDE中,∠BAE=540°﹣140°×2﹣90°×2=80°.
25.解:(1)∵△ACB和△DCE都是等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△ACE与△BCD中,
∴△ACE≌△BCD(SAS),
∴AE=BD,
(2)∵AC=DC,
∴AC=CD=EC=CB,
△ACB≌△DCE(SAS);
由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC
∴∠DOM=90°,
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BCN(ASA),
∴CM=CN,
∴DM=AN,
△AON≌△DOM(AAS),
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL)
26.解:(1)∠AMQ=45°+α;理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°﹣α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α;
(2)PQ=MB;理由如下:
连接AQ,作ME⊥QB,如图所示:
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
即PQ=MB.
27.解:(1)△EAD≌△EA'D,其中∠EAD=∠EA'D,∠AED=∠A'ED,
∠ADE=∠A'DE;
(2)∠1=180°﹣2x,∠2=180°﹣2y;
(3)∵∠1+∠2=360°﹣2(x+y)=360°﹣2(180°﹣∠A)=2∠A.
规律为:∠1+∠2=2∠A.
28.证明:(1)①如图1,
∵AB⊥AD,AE⊥AC,
∴∠BAD=90°,∠CAE=90°,
∴∠1=∠2,
在△ABC和△ADE中,
∵
∴△ABC≌△ADE(SAS);
②如图1,
∵△ABC≌△ADE,
∴∠AEC=∠3,
在Rt△ACE中,∠ACE+∠AEC=90°,
∴∠BCE=90°,
∵AH⊥CD,AE=AC,
∴CH=HE,
∵∠AHE=∠BCE=90°,
∴BC∥FH,
∴==1,
∴BF=EF;
(2)结论仍然成立,理由是:
如图2所示,过E作MN∥AH,交BA、CD延长线于M、N,
∵∠CAE=90°,∠BAD=90°,
∴∠1+∠2=90°,∠1+∠CAD=90°,
∴∠2=∠CAD,
∵MN∥AH,
∴∠3=∠HAE,
∵∠ACH+∠CAH=90°,∠CAH+∠HAE=90°,
∴∠ACH=∠HAE,
∴∠3=∠ACH,
在△MAE和△DAC中,
∵
∴△MAE≌△DAC(ASA),
∴AM=AD,∵AB=AD,∴AB=AM,∵AF∥ME,∴==1,∴BF=EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 5 页 (共 15 页) 版权所有@21世纪教育网
