12.3 角的平分线的性质培优提高试题
文档属性
| 名称 | 12.3 角的平分线的性质培优提高试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 713.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-30 00:00:00 | ||
图片预览

文档简介
12.3 角的平分线的性质培优提高
本卷共三大题满分 120分 时间120分钟
一.选择题(每小题3分 共30分)
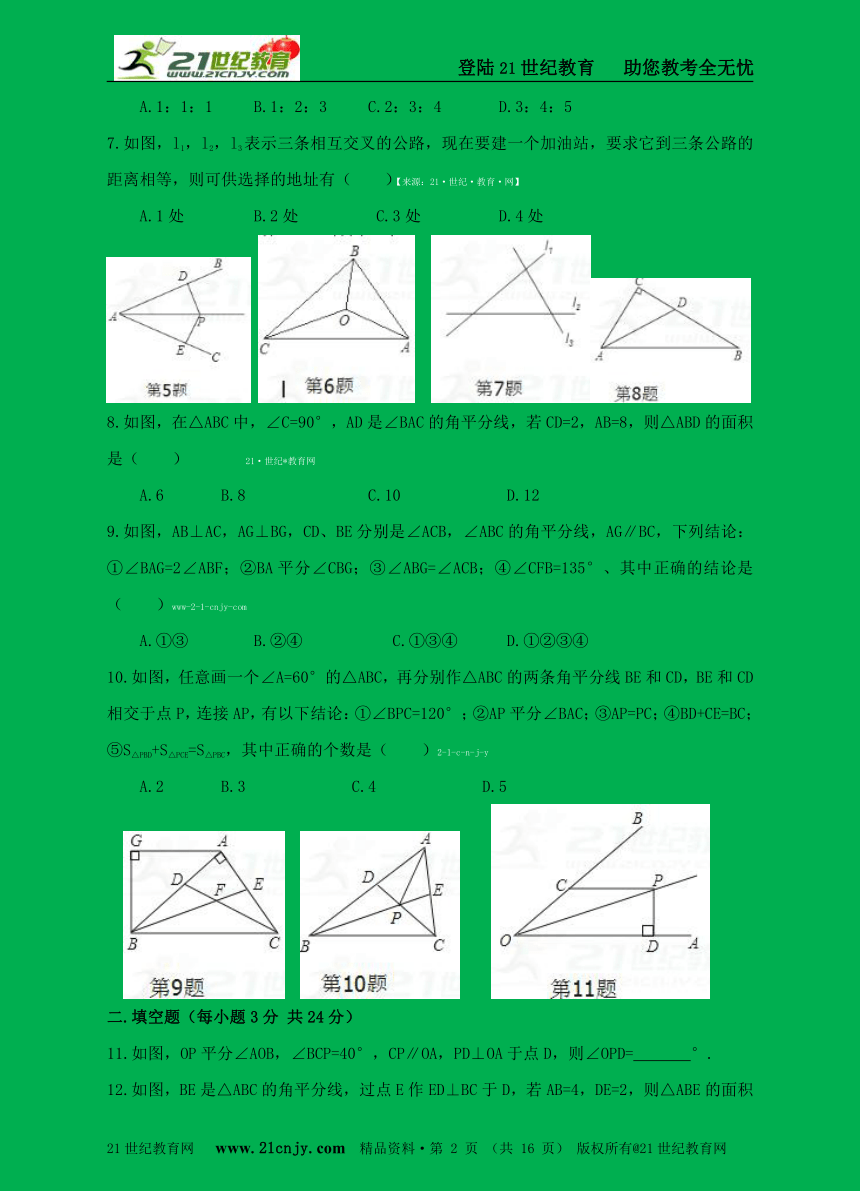
1.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,∠C的平分线与∠ABC的外角的平分线交于E点,则∠AEB是( )21世纪教育网版权所有
A.50° B.45° C.40° D.35°
2.如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )21cnjy.com
A.2 B.3 C.4 D.6
3.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
A.线段CD的中点 B.OA与OB的中垂线的交点
C.OA与CD的中垂线的交点 D.CD与∠AOB的平分线的交点
4.下列各图中,OP 是∠MON 的平分线,点E,F,G 分别在射线OM,ON,OP 上,则可以解释定理“角的平分线上的点到角的两边的距离相等”的图形是( )
B. C. D.
5.如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )21·cn·jy·com
A.SAS B.AAS C.SSS D.HL
6.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )2·1·c·n·j·y
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )【来源:21·世纪·教育·网】
A.1处 B.2处 C.3处 D.4处
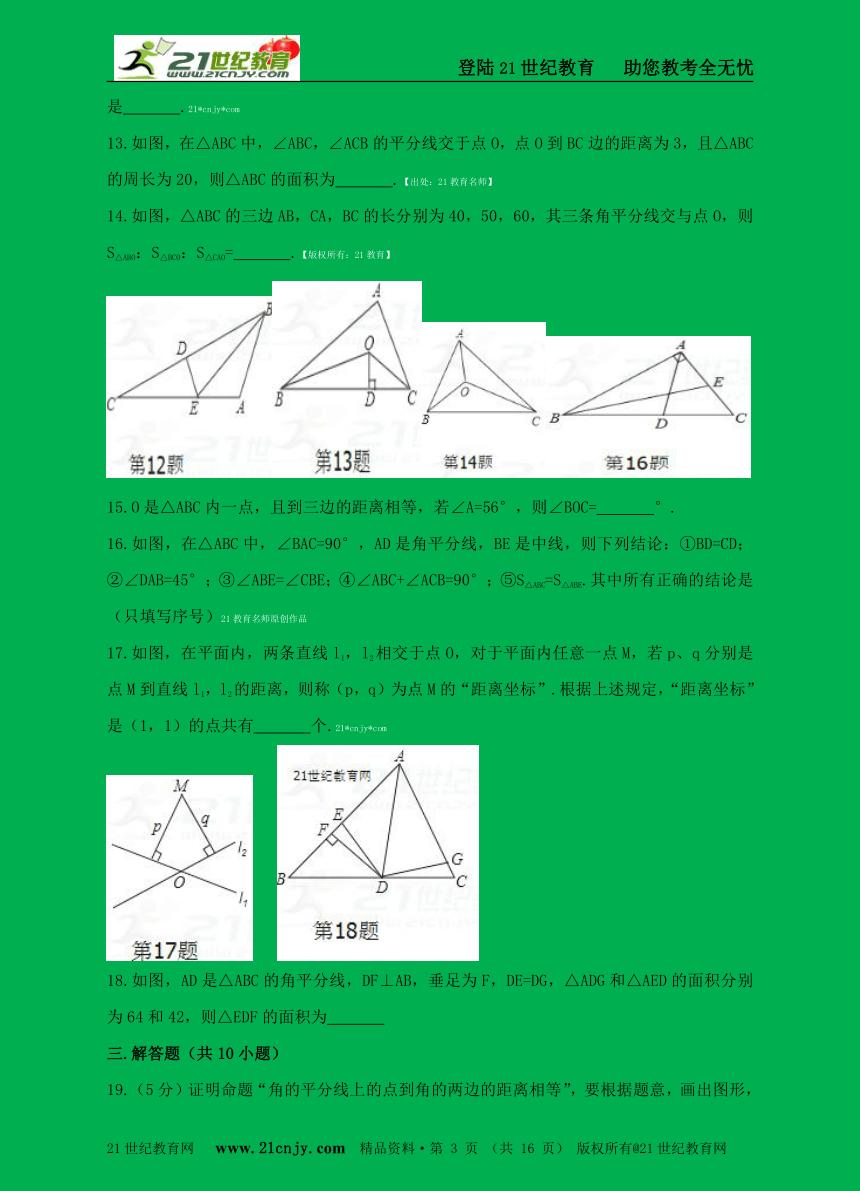
8.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是( ) 21·世纪*教育网
A.6 B.8 C.10 D.12
9.如图,AB⊥AC,AG⊥BG,CD、BE分别是∠ACB,∠ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°、其中正确的结论是( )www-2-1-cnjy-com
A.①③ B.②④ C.①③④ D.①②③④
10.如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AP=PC;④BD+CE=BC;⑤S△PBD+S△PCE=S△PBC,其中正确的个数是( )2-1-c-n-j-y
A.2 B.3 C.4 D.5
二.填空题(每小题3分 共24分)
11.如图,OP平分∠AOB,∠BCP=40°,CP∥OA,PD⊥OA于点D,则∠OPD= °.
12.如图,BE是△ABC的角平分线,过点E作ED⊥BC于D,若AB=4,DE=2,则△ABE的面积是 .21*cnjy*com
13.如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,点O到BC边的距离为3,且△ABC的周长为20,则△ABC的面积为 .【出处:21教育名师】
14.如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO= .【版权所有:21教育】
15.O是△ABC内一点,且到三边的距离相等,若∠A=56°,则∠BOC= °.
16.如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论:①BD=CD;②∠DAB=45°;③∠ABE=∠CBE;④∠ABC+∠ACB=90°;⑤S△ABC=S△ABE.其中所有正确的结论是 (只填写序号)21教育名师原创作品
17.如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p、q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(1,1)的点共有 个.21*cnjy*com
18.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为64和42,则△EDF的面积为
三.解答题(共10小题)
19.(5分)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,
求证: .
请你补全已知和求证,并写出证明过程.
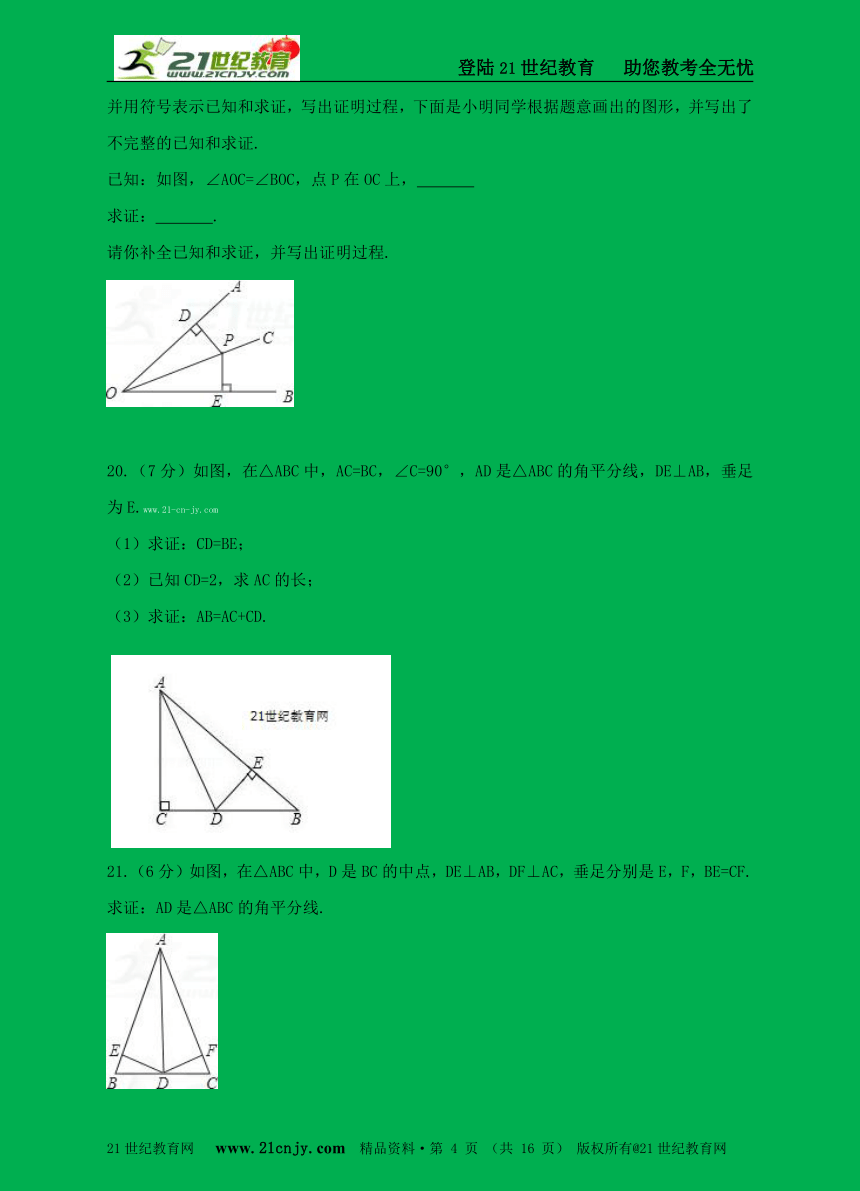
20.(7分)如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.www.21-cn-jy.com
(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
21.(6分)如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
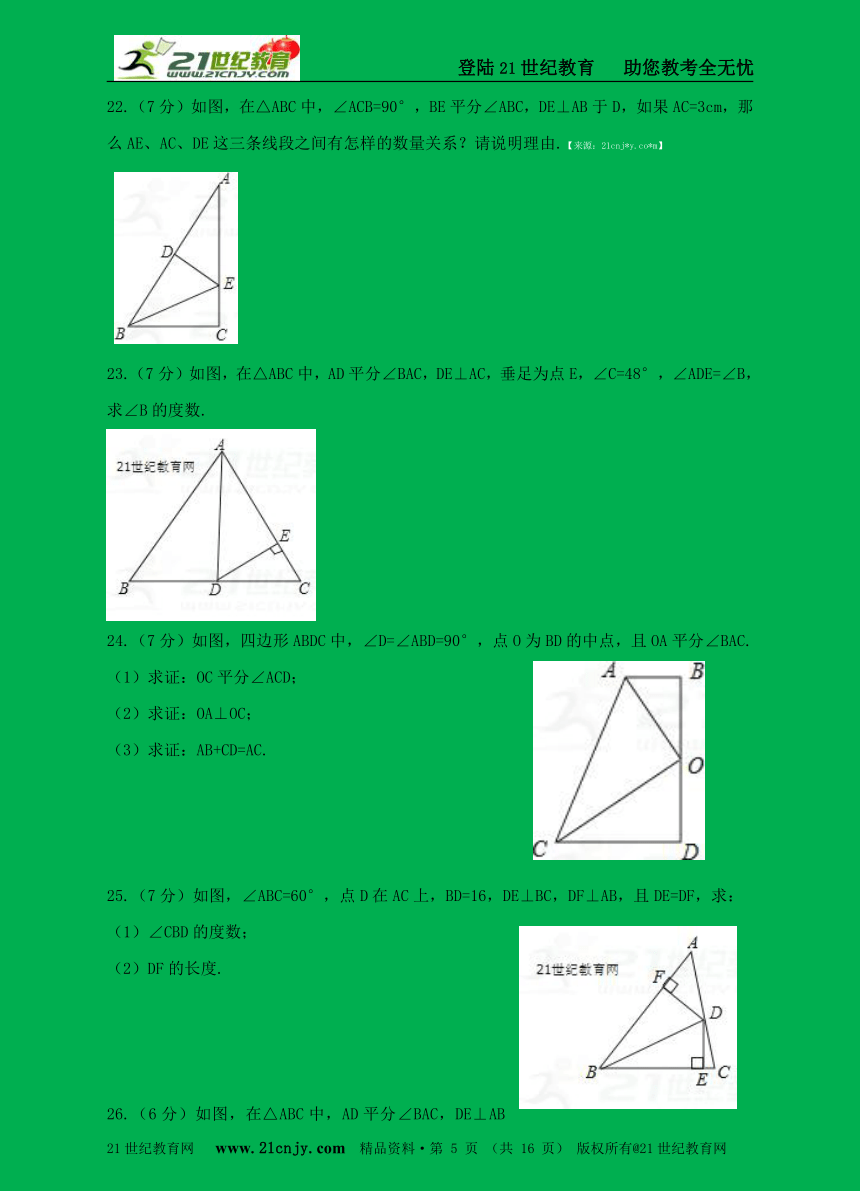
22.(7分)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE、AC、DE这三条线段之间有怎样的数量关系?请说明理由.【来源:21cnj*y.co*m】
23.(7分)如图,在△ABC中,AD平分∠BAC,DE⊥AC,垂足为点E,∠C=48°,∠ADE=∠B,求∠B的度数.
24.(7分)如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.
25.(7分)如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求:
(1)∠CBD的度数;
(2)DF的长度.
26.(6分)如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=4,若S△ABD=9,求S△ACD.
27.(6分)如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=(AD+AB).问:∠1和∠2有何关系?
28.(8分)(1)如图1,在△ABC中,AD平分∠BAC交BC于D,DE⊥AB于E,DF⊥AC于F,则有相等关系DE=DF,AE=AF.
(2)如图2,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB、AC相交于M、N两点,其它条件不变,那么又有相等关系AM+ =2AF,请加以证明.
(3)如图3,在Rt△ABC中,∠C=90°,∠BAC=60°,AC=6,AD平分∠BAC交BC于D,∠MDN=120°,ND∥AB,求四边形AMDN的周长.
2.解:∵P是∠AOB角平分线上的一点,∠AOB=60°,
∴∠AOP=∠AOB=30°,∴∠DPO=60°,∵PM=DM=4cm,∴∠MDP=∠DPM=60°,
∵∠PDO=90°,∴∠ODM=30°=∠AOP,∴OM=DM=4,∴OP=8,∴PD=OP=4,
∵点C是OB上一个动点,∴PC的最小值为P到OB距离,
∴PC的最小值=PD=4,故选C.
3.解:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交于点P.故选D.
4.解:∵OP是∠MON 的平分线,且GE⊥OM,GF⊥ON,
∴GE=GF,(角的平分线上的点到角的两边的距离相等)故选:D.
5.解:在△APD和△APE中,
,∴△APD≌△APE(AAS),故选:B.
6.解:利用同高不同底的三角形的面积之比就是底之比可知选C.故选C.
7.解:作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.故选D.
8.解:如图,过点D作DE⊥AB于E,
∵AB=8,CD=2,∵AD是∠BAC的角平分线,∠C=90°,∴DE=CD=2,
∴△ABD的面积=AB?DE=×8×2=8.故选B.
10.解:∵BE、CD分别是∠ABC与∠ACB的角平分线,∠BAC=60°,
∴∠PBC+∠PCB=(180°﹣∠BAC)=(180°﹣60°)=60°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣60°=120°,①正确;
∵∠BPC=120°,∴∠DPE=120°,
过点P作PF⊥AB,PG⊥AC,PH⊥BC,
∵BE、CD分别是∠ABC与∠ACB的角平分线,
∴AP是∠BAC的平分线,②正确;PF=PG=PH,
∵∠BAC=60°∠AFP=∠AGP=90°,∴∠FPG=120°,
∴∠DPF=∠EPG,在△PFD与△PGE中,,
∴△PFD≌△PGE(ASA),∴PD=PE,
在Rt△BHP与Rt△BFP中,,∴Rt△BHP≌Rt△BFP(HL),
同理,Rt△CHP≌Rt△CGP,∴BH=BD+DF,CH=CE﹣GE,
两式相加得,BH+CH=BD+DF+CE﹣GE,∵DF=EG,∴BC=BD+CE,④正确;
∴S△PBD+S△PCE=S△PBC,⑤正确;正确的个数有4个,故选:C.
二.填空题(每小题3分共24)
11. 70 °.
解:∵CP∥OA,
∴∠AOB=∠BCP=40°,
∵OP平分∠AOB,
∴∠AOP=∠AOB=20°,
∵PD⊥OA,
∴∠OPD=90°﹣20°=70°,
12. 6 .
解:过E作EF⊥AB于F,
∵ED⊥BC,BE是△ABC的角平分线,
∴ED=EF=2,
∴△ABE的面积=×AB?EF=3×4=6,故答案为:6.
13. 30 .
解:作OE⊥AB于E,OF⊥AC于F,连接OA,
∵OB是∠ABC的平分线,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理OF=OD=3,
△ABC的面积=×AB×3+×AC×3+×BC×3=30.故答案为:30.
14. 4:6:5 .
解:过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,
∵OA,OB,OC是△ABC的三条角平分线,
∴OD=OE=OF,
∵△ABC的三边AB、BC、CA长分别为40、50、60,
∴S△ABO:S△BCO:S△CAO=(AB?OD):(BC?OF):(AC?OE)=AB:BC:AC=40:50:60=4:5:6.故答案为:4:5:6.21教育网
15.118 °.
解:∵O到三角形三边距离相等,∴O是内心,
∴AO,BO,CO都是角平分线,
∴∠CBO=∠ABO=∠ABC,∠BCO=∠ACO=∠ACB,
∠ABC+∠ACB=180°﹣56°=124°,
∠OBC+∠OCB=62°,
∠BOC=180°﹣62°=118°.故答案为:118.
16. ②④
解:∵AD是角平分线,
∴BD与CD不一定相等,①错误;
∵∠BAC=90°,AD是角平分线,
∴∠DAB=∠BAC=45°,②正确;
∵BE是中线,
∴∠ABE与∠CBE不一定相等,③错误;
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,④正确;
由图形可知,S△ABC>S△ABE,⑤错误,故答案为:②④.
17. 4 .
解:到l1的距离是1的点,在与l1平行且与l1的距离是1的两条直线上;
到l2的距离是1的点,在与l2平行且与l2的距离是1的两条直线上;
以上四条直线有四个交点,故“距离坐标”是(1,1)的点共有4个.
18. 12 .
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,∴DF=DH,
在Rt△ADF和Rt△ADH中,,∴Rt△ADF≌Rt△ADH(HL),
∴SRt△ADF=SRt△ADH,
在Rt△DEF和Rt△DGH中,,∴Rt△DEF≌Rt△DGH(HL),
∴SRt△DEF=SRt△DGH,
∵△ADG和△AED的面积分别为64和42,
∴42+SRt△DEF=64﹣SRt△DGH,∴SRt△DEF=12.故答案为12.
三.解答题(共10小题总共66分)
(2)解:∵由(1)知,△BDE是等腰直角三角形,DE=BE=CD,
∴DE=BE=CD=2,
∴BD===2,
∴AC=BC=CD+BD=2+2;
(3)证明:∵AD是△ABC的角平分线,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
∵,∴Rt△ACD≌Rt△AED,
∴AE=AC.
∵由(1)知CD=BE,
∴AB=AE+BE=AC+CD.
21.证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△DCF是直角三角形.
,∴Rt△BDE≌Rt△DCF(HL),∴DE=DF,
又∵DE⊥AB,DF⊥AC,∴AD是角平分线.
22.解:AE+DE=AC=3cm.
理由如下:∵∠ACB=90°,BE平分∠ABC,DE⊥AB,
∴DE=CE,
由图可知,AC=AE+CE,
所以,AC=AE+DE=3cm.
23.解:∵DE⊥AC,
∴∠DEC=90°,
∴∠CDE=90°﹣∠C=42°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,又∠ADE=∠B,
∴∠ADC=∠AED=90°,
∴∠ADE=90°﹣∠CDE=48°,
∴∠B=48°.
24.证明:(1)过点O作OE⊥AC于E,
∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=×180°=90°,
∴OA⊥OC;
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
27.略证:∠1与∠2互补.
法1:作CF⊥AN于F(如图),
∵∠3=∠4,CE⊥AM,
∴CF=CE,∠CFA=∠CEA=90°,
Rt△ACF≌Rt△ACE,
∴AF=AE.
∵AE=(AD+AB)=(AF﹣DF+AE+EB)=AE+(BE﹣DF),
∴BE﹣DF=0,
∴BE=DF,
∴△DFC≌△BEC(SAS),
∴∠5=∠2,
∵∠1+∠5=180°,
∴∠1+∠2=180°;
法2:在AM上截取AF=AD,连接CF(如图),
∵∠3=∠4,AC为公共边,
∴△ADC≌△AFC,
∴∠1=∠5,
∵AE=(AD+AB)=(AF+AE+EB)=(AE﹣EF+AE+EB),
∴EB﹣EF=0,所以EF=EB,
又∵CE⊥AB,
∴BC=FC,∴∠2=∠6,
∵∠5+∠6=180°,
∴∠1+∠2=180°.
28.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△ADE和△ADF中,
,
∴△ADE≌△ADF(AAS),
∴DE=DF,AE=AF;
(2)解:AM+AN=2AF;
证明如下:由(1)得DE=DF,
∵∠MDN=∠EDF,
∴∠MDE=∠NDF,
在△MDE和△NDF中,
,
∴△MDE≌△NDF(ASA),
∴ME=NF,
∴AM+AN=(AE+ME)+(AF﹣NF)=AE+AF=2AF;
(3)由(2)可知AM+AN=2AC=2×6=12,
∵∠BAC=60°,AD平分∠BAC交BC于D,
∴∠BAD=∠CAD=30°,
∵ND∥AB,
∴∠ADN=∠BAD=30°,
∴∠CAD=∠ADN,
∴AN=DN,
在Rt△CDN中,DN=2CN,
∵AC=6,
∴DN=AN=×6=4,
∵∠BAC=60°,∠MDN=120°,
∴∠CDE=∠MDN,
∴DM=DN=4,
∴四边形AMDN的周长=12+4×2=20.
本卷共三大题满分 120分 时间120分钟
一.选择题(每小题3分 共30分)
1.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,∠C的平分线与∠ABC的外角的平分线交于E点,则∠AEB是( )21世纪教育网版权所有
A.50° B.45° C.40° D.35°
2.如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )21cnjy.com
A.2 B.3 C.4 D.6
3.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
A.线段CD的中点 B.OA与OB的中垂线的交点
C.OA与CD的中垂线的交点 D.CD与∠AOB的平分线的交点
4.下列各图中,OP 是∠MON 的平分线,点E,F,G 分别在射线OM,ON,OP 上,则可以解释定理“角的平分线上的点到角的两边的距离相等”的图形是( )
B. C. D.
5.如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )21·cn·jy·com
A.SAS B.AAS C.SSS D.HL
6.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )2·1·c·n·j·y
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )【来源:21·世纪·教育·网】
A.1处 B.2处 C.3处 D.4处
8.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是( ) 21·世纪*教育网
A.6 B.8 C.10 D.12
9.如图,AB⊥AC,AG⊥BG,CD、BE分别是∠ACB,∠ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°、其中正确的结论是( )www-2-1-cnjy-com
A.①③ B.②④ C.①③④ D.①②③④
10.如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AP=PC;④BD+CE=BC;⑤S△PBD+S△PCE=S△PBC,其中正确的个数是( )2-1-c-n-j-y
A.2 B.3 C.4 D.5
二.填空题(每小题3分 共24分)
11.如图,OP平分∠AOB,∠BCP=40°,CP∥OA,PD⊥OA于点D,则∠OPD= °.
12.如图,BE是△ABC的角平分线,过点E作ED⊥BC于D,若AB=4,DE=2,则△ABE的面积是 .21*cnjy*com
13.如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,点O到BC边的距离为3,且△ABC的周长为20,则△ABC的面积为 .【出处:21教育名师】
14.如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO= .【版权所有:21教育】
15.O是△ABC内一点,且到三边的距离相等,若∠A=56°,则∠BOC= °.
16.如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论:①BD=CD;②∠DAB=45°;③∠ABE=∠CBE;④∠ABC+∠ACB=90°;⑤S△ABC=S△ABE.其中所有正确的结论是 (只填写序号)21教育名师原创作品
17.如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p、q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(1,1)的点共有 个.21*cnjy*com
18.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为64和42,则△EDF的面积为
三.解答题(共10小题)
19.(5分)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,
求证: .
请你补全已知和求证,并写出证明过程.
20.(7分)如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.www.21-cn-jy.com
(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
21.(6分)如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
22.(7分)如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE、AC、DE这三条线段之间有怎样的数量关系?请说明理由.【来源:21cnj*y.co*m】
23.(7分)如图,在△ABC中,AD平分∠BAC,DE⊥AC,垂足为点E,∠C=48°,∠ADE=∠B,求∠B的度数.
24.(7分)如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.
25.(7分)如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求:
(1)∠CBD的度数;
(2)DF的长度.
26.(6分)如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=4,若S△ABD=9,求S△ACD.
27.(6分)如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=(AD+AB).问:∠1和∠2有何关系?
28.(8分)(1)如图1,在△ABC中,AD平分∠BAC交BC于D,DE⊥AB于E,DF⊥AC于F,则有相等关系DE=DF,AE=AF.
(2)如图2,在(1)的情况下,如果∠MDN=∠EDF,∠MDN的两边分别与AB、AC相交于M、N两点,其它条件不变,那么又有相等关系AM+ =2AF,请加以证明.
(3)如图3,在Rt△ABC中,∠C=90°,∠BAC=60°,AC=6,AD平分∠BAC交BC于D,∠MDN=120°,ND∥AB,求四边形AMDN的周长.
2.解:∵P是∠AOB角平分线上的一点,∠AOB=60°,
∴∠AOP=∠AOB=30°,∴∠DPO=60°,∵PM=DM=4cm,∴∠MDP=∠DPM=60°,
∵∠PDO=90°,∴∠ODM=30°=∠AOP,∴OM=DM=4,∴OP=8,∴PD=OP=4,
∵点C是OB上一个动点,∴PC的最小值为P到OB距离,
∴PC的最小值=PD=4,故选C.
3.解:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交于点P.故选D.
4.解:∵OP是∠MON 的平分线,且GE⊥OM,GF⊥ON,
∴GE=GF,(角的平分线上的点到角的两边的距离相等)故选:D.
5.解:在△APD和△APE中,
,∴△APD≌△APE(AAS),故选:B.
6.解:利用同高不同底的三角形的面积之比就是底之比可知选C.故选C.
7.解:作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.故选D.
8.解:如图,过点D作DE⊥AB于E,
∵AB=8,CD=2,∵AD是∠BAC的角平分线,∠C=90°,∴DE=CD=2,
∴△ABD的面积=AB?DE=×8×2=8.故选B.
10.解:∵BE、CD分别是∠ABC与∠ACB的角平分线,∠BAC=60°,
∴∠PBC+∠PCB=(180°﹣∠BAC)=(180°﹣60°)=60°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣60°=120°,①正确;
∵∠BPC=120°,∴∠DPE=120°,
过点P作PF⊥AB,PG⊥AC,PH⊥BC,
∵BE、CD分别是∠ABC与∠ACB的角平分线,
∴AP是∠BAC的平分线,②正确;PF=PG=PH,
∵∠BAC=60°∠AFP=∠AGP=90°,∴∠FPG=120°,
∴∠DPF=∠EPG,在△PFD与△PGE中,,
∴△PFD≌△PGE(ASA),∴PD=PE,
在Rt△BHP与Rt△BFP中,,∴Rt△BHP≌Rt△BFP(HL),
同理,Rt△CHP≌Rt△CGP,∴BH=BD+DF,CH=CE﹣GE,
两式相加得,BH+CH=BD+DF+CE﹣GE,∵DF=EG,∴BC=BD+CE,④正确;
∴S△PBD+S△PCE=S△PBC,⑤正确;正确的个数有4个,故选:C.
二.填空题(每小题3分共24)
11. 70 °.
解:∵CP∥OA,
∴∠AOB=∠BCP=40°,
∵OP平分∠AOB,
∴∠AOP=∠AOB=20°,
∵PD⊥OA,
∴∠OPD=90°﹣20°=70°,
12. 6 .
解:过E作EF⊥AB于F,
∵ED⊥BC,BE是△ABC的角平分线,
∴ED=EF=2,
∴△ABE的面积=×AB?EF=3×4=6,故答案为:6.
13. 30 .
解:作OE⊥AB于E,OF⊥AC于F,连接OA,
∵OB是∠ABC的平分线,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理OF=OD=3,
△ABC的面积=×AB×3+×AC×3+×BC×3=30.故答案为:30.
14. 4:6:5 .
解:过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,
∵OA,OB,OC是△ABC的三条角平分线,
∴OD=OE=OF,
∵△ABC的三边AB、BC、CA长分别为40、50、60,
∴S△ABO:S△BCO:S△CAO=(AB?OD):(BC?OF):(AC?OE)=AB:BC:AC=40:50:60=4:5:6.故答案为:4:5:6.21教育网
15.118 °.
解:∵O到三角形三边距离相等,∴O是内心,
∴AO,BO,CO都是角平分线,
∴∠CBO=∠ABO=∠ABC,∠BCO=∠ACO=∠ACB,
∠ABC+∠ACB=180°﹣56°=124°,
∠OBC+∠OCB=62°,
∠BOC=180°﹣62°=118°.故答案为:118.
16. ②④
解:∵AD是角平分线,
∴BD与CD不一定相等,①错误;
∵∠BAC=90°,AD是角平分线,
∴∠DAB=∠BAC=45°,②正确;
∵BE是中线,
∴∠ABE与∠CBE不一定相等,③错误;
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,④正确;
由图形可知,S△ABC>S△ABE,⑤错误,故答案为:②④.
17. 4 .
解:到l1的距离是1的点,在与l1平行且与l1的距离是1的两条直线上;
到l2的距离是1的点,在与l2平行且与l2的距离是1的两条直线上;
以上四条直线有四个交点,故“距离坐标”是(1,1)的点共有4个.
18. 12 .
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,∴DF=DH,
在Rt△ADF和Rt△ADH中,,∴Rt△ADF≌Rt△ADH(HL),
∴SRt△ADF=SRt△ADH,
在Rt△DEF和Rt△DGH中,,∴Rt△DEF≌Rt△DGH(HL),
∴SRt△DEF=SRt△DGH,
∵△ADG和△AED的面积分别为64和42,
∴42+SRt△DEF=64﹣SRt△DGH,∴SRt△DEF=12.故答案为12.
三.解答题(共10小题总共66分)
(2)解:∵由(1)知,△BDE是等腰直角三角形,DE=BE=CD,
∴DE=BE=CD=2,
∴BD===2,
∴AC=BC=CD+BD=2+2;
(3)证明:∵AD是△ABC的角平分线,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
∵,∴Rt△ACD≌Rt△AED,
∴AE=AC.
∵由(1)知CD=BE,
∴AB=AE+BE=AC+CD.
21.证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△DCF是直角三角形.
,∴Rt△BDE≌Rt△DCF(HL),∴DE=DF,
又∵DE⊥AB,DF⊥AC,∴AD是角平分线.
22.解:AE+DE=AC=3cm.
理由如下:∵∠ACB=90°,BE平分∠ABC,DE⊥AB,
∴DE=CE,
由图可知,AC=AE+CE,
所以,AC=AE+DE=3cm.
23.解:∵DE⊥AC,
∴∠DEC=90°,
∴∠CDE=90°﹣∠C=42°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,又∠ADE=∠B,
∴∠ADC=∠AED=90°,
∴∠ADE=90°﹣∠CDE=48°,
∴∠B=48°.
24.证明:(1)过点O作OE⊥AC于E,
∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=×180°=90°,
∴OA⊥OC;
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.
27.略证:∠1与∠2互补.
法1:作CF⊥AN于F(如图),
∵∠3=∠4,CE⊥AM,
∴CF=CE,∠CFA=∠CEA=90°,
Rt△ACF≌Rt△ACE,
∴AF=AE.
∵AE=(AD+AB)=(AF﹣DF+AE+EB)=AE+(BE﹣DF),
∴BE﹣DF=0,
∴BE=DF,
∴△DFC≌△BEC(SAS),
∴∠5=∠2,
∵∠1+∠5=180°,
∴∠1+∠2=180°;
法2:在AM上截取AF=AD,连接CF(如图),
∵∠3=∠4,AC为公共边,
∴△ADC≌△AFC,
∴∠1=∠5,
∵AE=(AD+AB)=(AF+AE+EB)=(AE﹣EF+AE+EB),
∴EB﹣EF=0,所以EF=EB,
又∵CE⊥AB,
∴BC=FC,∴∠2=∠6,
∵∠5+∠6=180°,
∴∠1+∠2=180°.
28.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在△ADE和△ADF中,
,
∴△ADE≌△ADF(AAS),
∴DE=DF,AE=AF;
(2)解:AM+AN=2AF;
证明如下:由(1)得DE=DF,
∵∠MDN=∠EDF,
∴∠MDE=∠NDF,
在△MDE和△NDF中,
,
∴△MDE≌△NDF(ASA),
∴ME=NF,
∴AM+AN=(AE+ME)+(AF﹣NF)=AE+AF=2AF;
(3)由(2)可知AM+AN=2AC=2×6=12,
∵∠BAC=60°,AD平分∠BAC交BC于D,
∴∠BAD=∠CAD=30°,
∵ND∥AB,
∴∠ADN=∠BAD=30°,
∴∠CAD=∠ADN,
∴AN=DN,
在Rt△CDN中,DN=2CN,
∵AC=6,
∴DN=AN=×6=4,
∵∠BAC=60°,∠MDN=120°,
∴∠CDE=∠MDN,
∴DM=DN=4,
∴四边形AMDN的周长=12+4×2=20.
