13.1-13.2轴对称和画轴对称图形培优提高试题
文档属性
| 名称 | 13.1-13.2轴对称和画轴对称图形培优提高试题 |
|
|
| 格式 | doc | ||
| 文件大小 | 995.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-30 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
13.1-13.2轴对称和轴对称图形培优提高
一.选择题(共10小题)
1.在下列“绿色食品、回收、节能、节水”四个标志中,是轴对称图形的是( )
A. B. C.
2.下列“数字”图形中,是轴对称图形有且仅有一条对称轴的是( )
A. B. C. D.
3.点P(﹣2,5)关于y轴对称的点的坐标为( )
A.(2,﹣5) B.(5,﹣2) C.(﹣2,﹣5) D.(2,5)
4.下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等 B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称 D.角是轴对称的图形
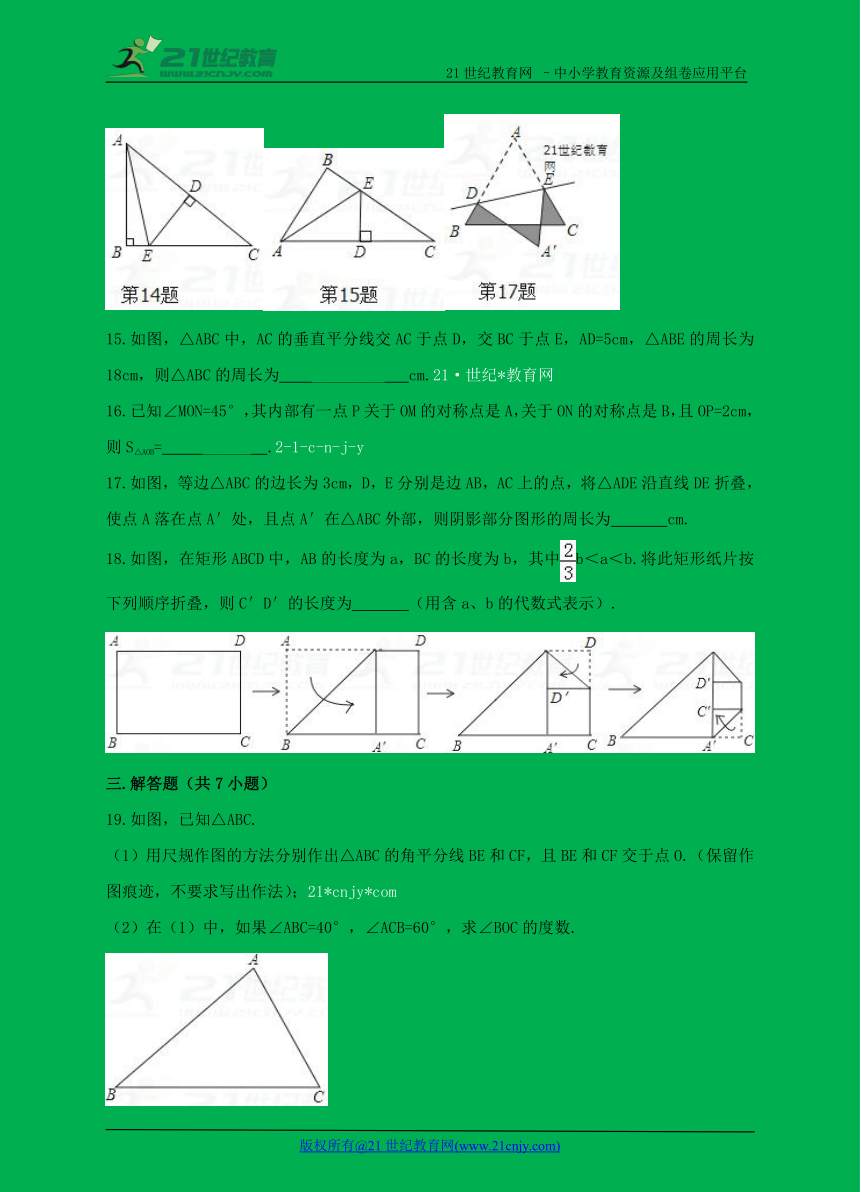
5.如图,四边形ABCD中,对角线AC垂直平分BD,垂足为点E,下列结论不一定成立的是( )
A.AB=AD B.CA平分∠BCD C.AB=BD D.△BEC≌△DEC
6.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
A.△ABC三边的垂直平分线的交点 B.△ABC的三条中线的交点
C.△ABC三条角平分线的交点 D.△ABC三条高所在直线的交点
7.如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是( )
A.1 号袋 B.2 号袋 C.3 号袋 D.4 号袋
8.点A,B关于直线a对称,P是直线a上的任意一点,下列说法不正确的是( )
A.直线AB与直线a垂直 B.直线a是点A和点B的对称轴
C.线段PA与线段PB相等 D.若PA=PB,则点P是线段AB的中点
9.图①为一张三角形ABC纸片,P点在BC上.今将A折至P时,出现折线BD,其中D点在AC上,如图②所示.若△ABC的面积为80,△DBC的面积为50,则BP与PC的长度比为( )
A.3:2 B.5:3 C.8:5 D.13:8
10.如图,△ABC的内部有一点P,且D,E,F是P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠A=70°,∠B=60°,∠C=50°,则∠ADB+∠BEC+∠CFA=( )
A.180° B.270° C.360° D.480°
二.填空题(共8小题)
11.直线l上有三个不同的点A、B、C,且AB=BC.有以下说法:
①线段AB和线段BC关于某一定点成中心对称;②线段AC是中心对称图形;③线段AB是中心对称图形;④直线l是中心对称图形.其中正确的说法有___________。
12.在直角坐标系中,点A(m,1)与点B(﹣3,n)关于x轴对称,则m+n= .
13.26个英文字母中,有很多都具有轴对称结构,请你写出其中具有轴对称结构的字母(至少3个) _______________.【来源:21·世纪·教育·网】
14.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠C=40°,则∠BAE的度数为 °.www-2-1-cnjy-com
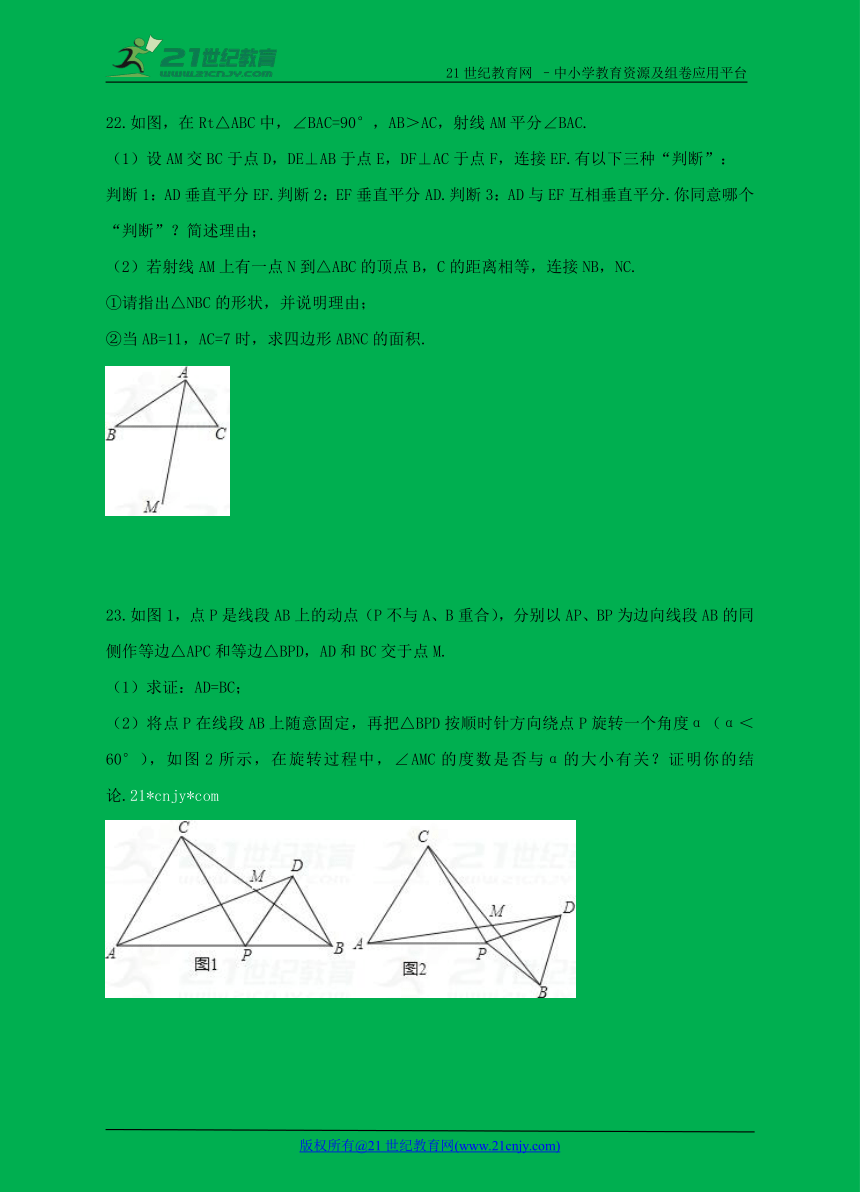
15.如图,△ABC中,AC的垂直平分线交AC于点D,交BC于点E,AD=5cm,△ABE的周长为18cm,则△ABC的周长为 _________ cm.21·世纪*教育网
16.已知∠MON=45°,其内部有一点P关于OM的对称点是A,关于ON的对称点是B,且OP=2cm,则S△AOB= ______ .2-1-c-n-j-y
17.如图,等边△ABC的边长为3cm,D,E分别是边AB,AC上的点,将△ADE沿直线DE折叠,使点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
18.如图,在矩形ABCD中,AB的长度为a,BC的长度为b,其中b<a<b.将此矩形纸片按下列顺序折叠,则C′D′的长度为 (用含a、b的代数式表示).
三.解答题(共7小题)
19.如图,已知△ABC.
(1)用尺规作图的方法分别作出△ABC的角平分线BE和CF,且BE和CF交于点O.(保留作图痕迹,不要求写出作法);21*cnjy*com
(2)在(1)中,如果∠ABC=40°,∠ACB=60°,求∠BOC的度数.
20.已知MN是线段AB的垂直平分线,C,D是MN上的两点.求证:
(1)△ABC,△ABD是等腰三角形;
(2)∠CAD=∠CBD.
21.已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(﹣3,0),点B的坐标为
(1,3).【出处:21教育名师】
(1)请画出△ABC;
(2)如果△ABC关于y轴对称的三角形为△A1B1C1,请写出△A1B1C1三个顶点的坐标:
点A的对称点A1的坐标是 ,点B的对称点B1的坐标是 ,点C的对称点C1的坐标是 ;【版权所有:21教育】
(3)如果点D的坐标为(5,﹣3),将△ABC左右平移,使点C与点D重合,那么点A平移的方向是 ,距离是 个单位.21教育名师原创作品
22.如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.判断2:EF垂直平分AD.判断3:AD与EF互相垂直平分.你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
23.如图1,点P是线段AB上的动点(P不与A、B重合),分别以AP、BP为边向线段AB的同侧作等边△APC和等边△BPD,AD和BC交于点M.
(1)求证:AD=BC;
(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α(α<60°),如图2所示,在旋转过程中,∠AMC的度数是否与α的大小有关?证明你的结论.21*cnjy*com
24.如图,在△ABC中,DE垂直平分AB,分别交AB、BC于D、E点.MN垂直平分AC,分别交AC、BC于M、N点.
(1)若∠BAC=100°,求∠EAN的度数;
(2)若∠BAC=70°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
25.如图1,在△ABC中,点D、E在边BC上,且使BD=BA,CE=CA,则点D、E叫做△ABC的一对“等腰点”.
(1)如图1,当AB=AC<BC时,则图中有 个等腰三角形,它们分别是 .
(2)如图2,D、E是△ABC的一对“等腰点”,当∠BAC=90°,∠B=50°时,求∠EAD的度数.2·1·c·n·j·y
(3)如图3,D、E是△ABC的一对“等腰点”,若∠BAC=m(90°≤m<180°),求∠α的度数(用含m的代数式表示)21教育网
5 C.【解答】解:∵对角线AC垂直平分BD,∴AB=AD,BC=BD,故A正确;
∵BC=CD,AC⊥BD,∴CA平分∠BCD,故B正确;∵AC垂直平分BD,
∴BE=DE,BC=CD,在Rt△BEC与Rt△DEC中,∵,
∴△BEC≌△DEC(HL),故D正确.
6A.【解答】解:∵凉亭到草坪三条边的距离相等,∴凉亭选择△ABC三条角平分线的交点.
7B.【解答】解:如图所示,该球最后落入2号袋.
8D.【解答】解:A、直线AB与直线a垂直,故本选项正确;
B、直线a是点A和点B的对称轴,故本选项正确;
C、线段PA与线段PB相等,故本选项正确;
D、若PA=PB,则P可是直线a上的任意一点,故本选项错误.
9A.【解答】解:由题意可得:S△ABD=S△ABC﹣S△DBC=80﹣50=30.由折叠性质可知
S△DBP=S△ABD=30,∴S△DCP=S△DBC﹣S△DBP=50﹣30=20.
∴BP:PC=S△DBP:S△DCP=30:20=3:2.
10C.【解答】解:连接AP,BP,CP,∵D,E,F是P分别以AB,BC,AC为对称轴的对称点∴∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,
∴∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
二.填空题(共8小题)
16.2cm2.【解答】解:∵点P关于OM的对称点是A,∴OA=OP,∠AOM=∠MOP,
∵点P关于ON的对称点是B,∴OB=OP,∠BON=∠BOP,
∴OA=OB=OP,∠AOB=∠AOM+∠MOP+∠BON+∠BOP=2(∠MOP+∠NOP)=2∠MON=2×45°=90°,∴△AOB是等腰直角三角形,
∵OP=2cm,∴S△AOB=×22=2cm2.
17. 9 cm.【解答】解:将△ADE沿直线DE折叠,点A落在点A′处,∴AD=A′D,AE=A′E.则阴影部分图形的周长等于BC+BD+CE+A′D+A′E
=BC+BD+CE+AD+AE=BC+AB+AC=9.
18.3a﹣2b(用含a、b的代数式表示).
【解答】解:由轴对称可以得出A′B=AB=a,∵BC=b,∴A′C=b﹣a.
由轴对称可以得出A′C′=b﹣a,∴C′D′=a﹣2(b﹣a),∴C′D′=3a﹣2b.
三.解答题(共7小题)
19.【解答】解:(1)如图,线段BE、CF和点O为所作;
(2)解:∵BE平分∠ABC,CF平分∠ACB,
∴∠EBC=∠ABC=20°,∠FCB=∠ACB=30°,
∴∠BOC=180°﹣20°﹣30°=130°.
20.【解答】证明:(1)∵MN是线段AB的垂直平分线,C,D是MN上的两点.
∴AC=BC,AD=BD,即△ABC,△ABD是等腰三角形;
(2)∵AC=BC,AD=BD,
∴∠CAB=∠CBA,∠DAB=∠DBA,
∴∠CAB+∠DAB=∠CBA+∠DBA,
即∠CAD=∠CBD.
21.【解答】解:(1)△ABC即为所求;
(2)如图所示:△A1B1C1,即为所求,A1(3,0),B1(﹣1,3),C1(﹣1,﹣3).
(3)如图,∵点D的坐标为(5,﹣3),将△ABC左右平移,使点C与点D重合,则点C平移的方向是向右,距离是4个单位∴点A平移的方向是向右,距离是4个单位.故答案为:向右,4.21世纪教育网版权所有
22.【解答】解:(1)如图,判断3正确.理由如下:
∵∠BAC=90°,DE⊥ABDF⊥AC,∴DE=DF,∴∠AED=∠AFD=∠EAF=90°,
∴四边形AEDF是矩形,∵DE=DF,∴四边形AEDF是正方形,
∴AD与EF互相垂直平分.故判断3正确.
(2)①结论:△BCN是等腰直角三角形.理由如下:
如图作NE⊥AB于E,FN⊥AC于F.
.
23.【解答】解:(1)如图1,∵△APC和△BPD是等边三角形,
∴CP=AP,DP=PB,∠APC=∠DPB=60°,
∵∠BPC=180°﹣60°,∠DPA=180°﹣60°,∴∠BPC=∠DPA,
在△BPC和△DPA中,
,∴△BPC≌△DPA,∴AD=BC.
(2)∠AMC的度数与α的大小无关,理由如下:
如图2,∵∠BPC=∠CPD+60°,∠DPA=∠CPD+60°,∴∠BPC=∠DPA,
在△BPC和△DPA中,,∴△BPC≌△DPA,∴∠BCP=∠DAP,
∴∠AMC=180°﹣∠MCP﹣∠PCA﹣∠MAC
=120°﹣∠BCP﹣∠MAC
=120°﹣(∠DAP+∠MAC)
=120°﹣∠PAC
=60°,
∴∠AMC的度数与α无关.
24.【解答】解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得:∠CAN=∠C,∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,
=∠BAC﹣(∠B+∠C),
在△ABC中,∠B+∠C=180°﹣∠BAC=80°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=100°﹣80°=20°;
(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN﹣∠BAC,
=(∠B+∠C)﹣∠BAC,
在△ABC中,∠B+∠C=180°﹣∠BAC=110°,
∴∠EAN=∠BAE+∠CAN﹣∠BAC=110°﹣70°=40°;
(3)当α<90°时,∠EAN=180°﹣2α;
当α>90°时,∠EAN=2α﹣180°.
(2)∵∠BAC=90°,∠B=50°,∴∠C=90°﹣50°=40°,∵BD=BA,CE=CA,
∴∠BDA=(180°﹣50°)=65°,∠CEA=(180°﹣40°)=70°,
∴∠EAD=180°﹣65°﹣70°=45°;
(3)∵BD=BA,CE=CA,
∴∠BDA=(180°﹣∠B),∠CEA=(180°﹣∠C),
∴∠BDA+∠CEA=180°﹣(∠B+∠C),
∴∠EAD=∠α=180°﹣(∠BDA+∠CEA)=(∠B+∠C),
∵∠B+∠C=180°﹣∠BAC=180°﹣m,∴∠α=90°﹣.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
13.1-13.2轴对称和轴对称图形培优提高
一.选择题(共10小题)
1.在下列“绿色食品、回收、节能、节水”四个标志中,是轴对称图形的是( )
A. B. C.
2.下列“数字”图形中,是轴对称图形有且仅有一条对称轴的是( )
A. B. C. D.
3.点P(﹣2,5)关于y轴对称的点的坐标为( )
A.(2,﹣5) B.(5,﹣2) C.(﹣2,﹣5) D.(2,5)
4.下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等 B.轴对称图形至少有一条对称轴
C.全等三角形一定能关于某条直线对称 D.角是轴对称的图形
5.如图,四边形ABCD中,对角线AC垂直平分BD,垂足为点E,下列结论不一定成立的是( )
A.AB=AD B.CA平分∠BCD C.AB=BD D.△BEC≌△DEC
6.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
A.△ABC三边的垂直平分线的交点 B.△ABC的三条中线的交点
C.△ABC三条角平分线的交点 D.△ABC三条高所在直线的交点
7.如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是( )
A.1 号袋 B.2 号袋 C.3 号袋 D.4 号袋
8.点A,B关于直线a对称,P是直线a上的任意一点,下列说法不正确的是( )
A.直线AB与直线a垂直 B.直线a是点A和点B的对称轴
C.线段PA与线段PB相等 D.若PA=PB,则点P是线段AB的中点
9.图①为一张三角形ABC纸片,P点在BC上.今将A折至P时,出现折线BD,其中D点在AC上,如图②所示.若△ABC的面积为80,△DBC的面积为50,则BP与PC的长度比为( )
A.3:2 B.5:3 C.8:5 D.13:8
10.如图,△ABC的内部有一点P,且D,E,F是P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠A=70°,∠B=60°,∠C=50°,则∠ADB+∠BEC+∠CFA=( )
A.180° B.270° C.360° D.480°
二.填空题(共8小题)
11.直线l上有三个不同的点A、B、C,且AB=BC.有以下说法:
①线段AB和线段BC关于某一定点成中心对称;②线段AC是中心对称图形;③线段AB是中心对称图形;④直线l是中心对称图形.其中正确的说法有___________。
12.在直角坐标系中,点A(m,1)与点B(﹣3,n)关于x轴对称,则m+n= .
13.26个英文字母中,有很多都具有轴对称结构,请你写出其中具有轴对称结构的字母(至少3个) _______________.【来源:21·世纪·教育·网】
14.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠C=40°,则∠BAE的度数为 °.www-2-1-cnjy-com
15.如图,△ABC中,AC的垂直平分线交AC于点D,交BC于点E,AD=5cm,△ABE的周长为18cm,则△ABC的周长为 _________ cm.21·世纪*教育网
16.已知∠MON=45°,其内部有一点P关于OM的对称点是A,关于ON的对称点是B,且OP=2cm,则S△AOB= ______ .2-1-c-n-j-y
17.如图,等边△ABC的边长为3cm,D,E分别是边AB,AC上的点,将△ADE沿直线DE折叠,使点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
18.如图,在矩形ABCD中,AB的长度为a,BC的长度为b,其中b<a<b.将此矩形纸片按下列顺序折叠,则C′D′的长度为 (用含a、b的代数式表示).
三.解答题(共7小题)
19.如图,已知△ABC.
(1)用尺规作图的方法分别作出△ABC的角平分线BE和CF,且BE和CF交于点O.(保留作图痕迹,不要求写出作法);21*cnjy*com
(2)在(1)中,如果∠ABC=40°,∠ACB=60°,求∠BOC的度数.
20.已知MN是线段AB的垂直平分线,C,D是MN上的两点.求证:
(1)△ABC,△ABD是等腰三角形;
(2)∠CAD=∠CBD.
21.已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(﹣3,0),点B的坐标为
(1,3).【出处:21教育名师】
(1)请画出△ABC;
(2)如果△ABC关于y轴对称的三角形为△A1B1C1,请写出△A1B1C1三个顶点的坐标:
点A的对称点A1的坐标是 ,点B的对称点B1的坐标是 ,点C的对称点C1的坐标是 ;【版权所有:21教育】
(3)如果点D的坐标为(5,﹣3),将△ABC左右平移,使点C与点D重合,那么点A平移的方向是 ,距离是 个单位.21教育名师原创作品
22.如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.判断2:EF垂直平分AD.判断3:AD与EF互相垂直平分.你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
23.如图1,点P是线段AB上的动点(P不与A、B重合),分别以AP、BP为边向线段AB的同侧作等边△APC和等边△BPD,AD和BC交于点M.
(1)求证:AD=BC;
(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α(α<60°),如图2所示,在旋转过程中,∠AMC的度数是否与α的大小有关?证明你的结论.21*cnjy*com
24.如图,在△ABC中,DE垂直平分AB,分别交AB、BC于D、E点.MN垂直平分AC,分别交AC、BC于M、N点.
(1)若∠BAC=100°,求∠EAN的度数;
(2)若∠BAC=70°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
25.如图1,在△ABC中,点D、E在边BC上,且使BD=BA,CE=CA,则点D、E叫做△ABC的一对“等腰点”.
(1)如图1,当AB=AC<BC时,则图中有 个等腰三角形,它们分别是 .
(2)如图2,D、E是△ABC的一对“等腰点”,当∠BAC=90°,∠B=50°时,求∠EAD的度数.2·1·c·n·j·y
(3)如图3,D、E是△ABC的一对“等腰点”,若∠BAC=m(90°≤m<180°),求∠α的度数(用含m的代数式表示)21教育网
5 C.【解答】解:∵对角线AC垂直平分BD,∴AB=AD,BC=BD,故A正确;
∵BC=CD,AC⊥BD,∴CA平分∠BCD,故B正确;∵AC垂直平分BD,
∴BE=DE,BC=CD,在Rt△BEC与Rt△DEC中,∵,
∴△BEC≌△DEC(HL),故D正确.
6A.【解答】解:∵凉亭到草坪三条边的距离相等,∴凉亭选择△ABC三条角平分线的交点.
7B.【解答】解:如图所示,该球最后落入2号袋.
8D.【解答】解:A、直线AB与直线a垂直,故本选项正确;
B、直线a是点A和点B的对称轴,故本选项正确;
C、线段PA与线段PB相等,故本选项正确;
D、若PA=PB,则P可是直线a上的任意一点,故本选项错误.
9A.【解答】解:由题意可得:S△ABD=S△ABC﹣S△DBC=80﹣50=30.由折叠性质可知
S△DBP=S△ABD=30,∴S△DCP=S△DBC﹣S△DBP=50﹣30=20.
∴BP:PC=S△DBP:S△DCP=30:20=3:2.
10C.【解答】解:连接AP,BP,CP,∵D,E,F是P分别以AB,BC,AC为对称轴的对称点∴∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,
∴∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
二.填空题(共8小题)
16.2cm2.【解答】解:∵点P关于OM的对称点是A,∴OA=OP,∠AOM=∠MOP,
∵点P关于ON的对称点是B,∴OB=OP,∠BON=∠BOP,
∴OA=OB=OP,∠AOB=∠AOM+∠MOP+∠BON+∠BOP=2(∠MOP+∠NOP)=2∠MON=2×45°=90°,∴△AOB是等腰直角三角形,
∵OP=2cm,∴S△AOB=×22=2cm2.
17. 9 cm.【解答】解:将△ADE沿直线DE折叠,点A落在点A′处,∴AD=A′D,AE=A′E.则阴影部分图形的周长等于BC+BD+CE+A′D+A′E
=BC+BD+CE+AD+AE=BC+AB+AC=9.
18.3a﹣2b(用含a、b的代数式表示).
【解答】解:由轴对称可以得出A′B=AB=a,∵BC=b,∴A′C=b﹣a.
由轴对称可以得出A′C′=b﹣a,∴C′D′=a﹣2(b﹣a),∴C′D′=3a﹣2b.
三.解答题(共7小题)
19.【解答】解:(1)如图,线段BE、CF和点O为所作;
(2)解:∵BE平分∠ABC,CF平分∠ACB,
∴∠EBC=∠ABC=20°,∠FCB=∠ACB=30°,
∴∠BOC=180°﹣20°﹣30°=130°.
20.【解答】证明:(1)∵MN是线段AB的垂直平分线,C,D是MN上的两点.
∴AC=BC,AD=BD,即△ABC,△ABD是等腰三角形;
(2)∵AC=BC,AD=BD,
∴∠CAB=∠CBA,∠DAB=∠DBA,
∴∠CAB+∠DAB=∠CBA+∠DBA,
即∠CAD=∠CBD.
21.【解答】解:(1)△ABC即为所求;
(2)如图所示:△A1B1C1,即为所求,A1(3,0),B1(﹣1,3),C1(﹣1,﹣3).
(3)如图,∵点D的坐标为(5,﹣3),将△ABC左右平移,使点C与点D重合,则点C平移的方向是向右,距离是4个单位∴点A平移的方向是向右,距离是4个单位.故答案为:向右,4.21世纪教育网版权所有
22.【解答】解:(1)如图,判断3正确.理由如下:
∵∠BAC=90°,DE⊥ABDF⊥AC,∴DE=DF,∴∠AED=∠AFD=∠EAF=90°,
∴四边形AEDF是矩形,∵DE=DF,∴四边形AEDF是正方形,
∴AD与EF互相垂直平分.故判断3正确.
(2)①结论:△BCN是等腰直角三角形.理由如下:
如图作NE⊥AB于E,FN⊥AC于F.
.
23.【解答】解:(1)如图1,∵△APC和△BPD是等边三角形,
∴CP=AP,DP=PB,∠APC=∠DPB=60°,
∵∠BPC=180°﹣60°,∠DPA=180°﹣60°,∴∠BPC=∠DPA,
在△BPC和△DPA中,
,∴△BPC≌△DPA,∴AD=BC.
(2)∠AMC的度数与α的大小无关,理由如下:
如图2,∵∠BPC=∠CPD+60°,∠DPA=∠CPD+60°,∴∠BPC=∠DPA,
在△BPC和△DPA中,,∴△BPC≌△DPA,∴∠BCP=∠DAP,
∴∠AMC=180°﹣∠MCP﹣∠PCA﹣∠MAC
=120°﹣∠BCP﹣∠MAC
=120°﹣(∠DAP+∠MAC)
=120°﹣∠PAC
=60°,
∴∠AMC的度数与α无关.
24.【解答】解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得:∠CAN=∠C,∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,
=∠BAC﹣(∠B+∠C),
在△ABC中,∠B+∠C=180°﹣∠BAC=80°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=100°﹣80°=20°;
(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN﹣∠BAC,
=(∠B+∠C)﹣∠BAC,
在△ABC中,∠B+∠C=180°﹣∠BAC=110°,
∴∠EAN=∠BAE+∠CAN﹣∠BAC=110°﹣70°=40°;
(3)当α<90°时,∠EAN=180°﹣2α;
当α>90°时,∠EAN=2α﹣180°.
(2)∵∠BAC=90°,∠B=50°,∴∠C=90°﹣50°=40°,∵BD=BA,CE=CA,
∴∠BDA=(180°﹣50°)=65°,∠CEA=(180°﹣40°)=70°,
∴∠EAD=180°﹣65°﹣70°=45°;
(3)∵BD=BA,CE=CA,
∴∠BDA=(180°﹣∠B),∠CEA=(180°﹣∠C),
∴∠BDA+∠CEA=180°﹣(∠B+∠C),
∴∠EAD=∠α=180°﹣(∠BDA+∠CEA)=(∠B+∠C),
∵∠B+∠C=180°﹣∠BAC=180°﹣m,∴∠α=90°﹣.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
