11.1-11.2 与三角形有关的线段和角培优提高
文档属性
| 名称 | 11.1-11.2 与三角形有关的线段和角培优提高 |

|
|
| 格式 | doc | ||
| 文件大小 | 950.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-09 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
八上数学第十一章培优提高 与三角形有关的线段和角
一.选择题(共10小题)
1.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=50°,则∠BPC的度数是( )21·cn·jy·com
A.100 B.120 C.130 D.150
2.若一个三角形的两个内角的平分线所成的钝角为145°,则这个三角形的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.两根木棒分别为5cm和7cm,要选择第三根,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有( )2·1·c·n·j·y
A.3种 B.4种 C.5种 D.6种
4.以长为8cm、6cm、10cm、4cm的四条线段中的三条线段为边,可以画出三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短 C.N点确定一条直线 D.垂线段最短
6.如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )【出处:21教育名师】
A.BD是△ABC的高 B.CD是△BCD的高 C.ME是△ABD的高 D.BE是△BMN的高
7.如图,已知△ABC中,∠B=50°,若沿图中虚线剪去∠B,则∠1+∠2等于( )
A.130° B.230° C.270° D.310°
8.下列说法正确的是( )
A.三角形的角平分线是射线
B.三角形的三条高一定在三角形内部
C.三角形的外角必大于每一个内角
D.三角形的一条中线把原三角形分成的两个小三角形面积相等
9.如图△ABC的两个外角的平分线交于点D,若∠B=60°,则∠D等于( )
A.60° B.80° C.65° D.30°
10.有5条线段,它们的长度分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长,可组成不同的三角形的个数为( )【版权所有:21教育】
A.3 B.4 C.5 D.6
二.填空题(共10小题)
11.如图,是一块三角形木板的残余部分,若量得∠A=100°,∠C=45°,则这块三角形木板另外一个角是 度.2-1-c-n-j-y
12.如图,△ABC中,AD平分∠BAC,AE是BC边上的高,若∠B=30°,∠C=70°,则∠DAE的度数等于 .www.21-cn-jy.com
13.某机器零件的横截面如图所示,按要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°,∠D=31°,∠AED=143°,请你帮他判断该零件是否合格 (填“合格”或“不合格”).21教育名师原创作品
14.已知三角形的两边长分别为2和7,第三边为奇数,则它第三边的长是 .
15.已知a,b,c是一个三角形的三条边长,则化简|a﹣b+c|﹣|b﹣a﹣c|= .
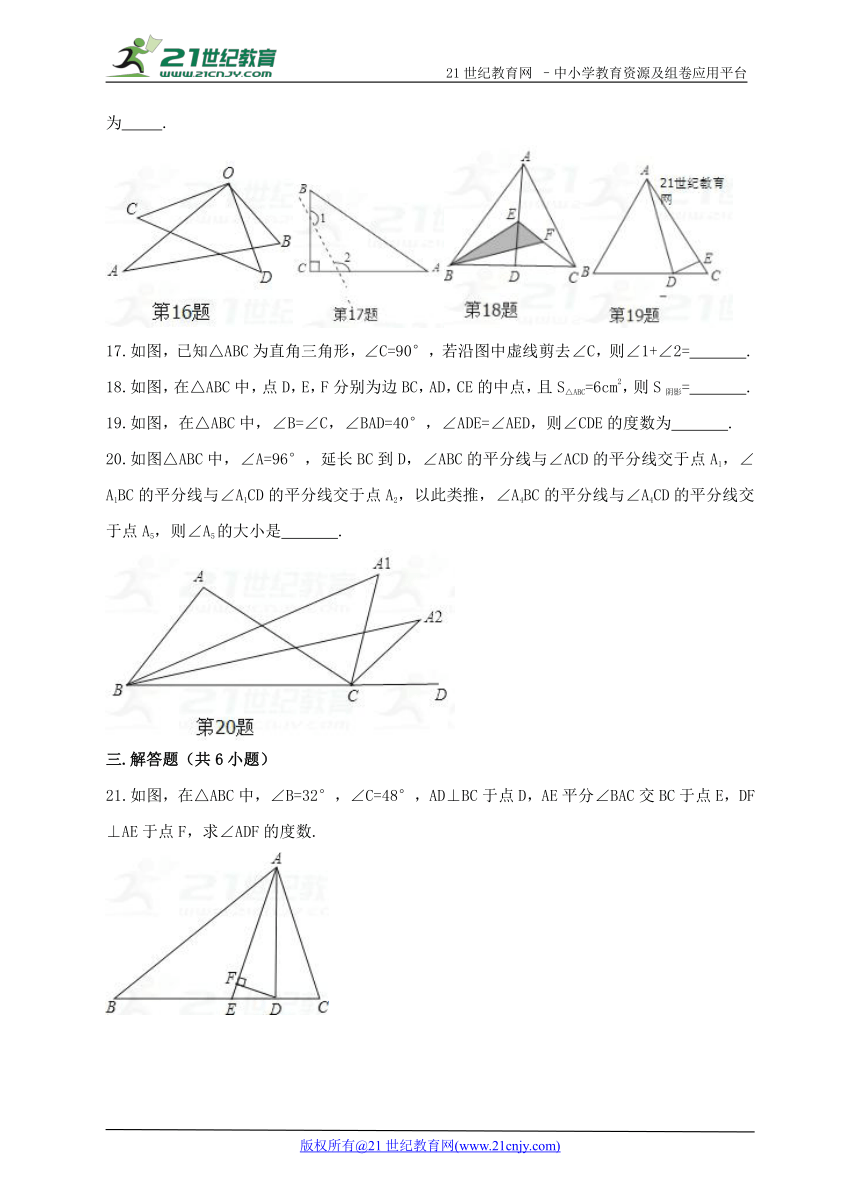
16.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOD+∠COB的度数为 .
17.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2= .
18.如图,在△ABC中,点D,E,F分别为边BC,AD,CE的中点,且S△ABC=6cm2,则S阴影= .
19.如图,在△ABC中,∠B=∠C,∠BAD=40°,∠ADE=∠AED,则∠CDE的度数为 .
20.如图△ABC中,∠A=96°,延长BC到D,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,以此类推,∠A4BC的平分线与∠A4CD的平分线交于点A5,则∠A5的大小是 .21教育网
三.解答题(共6小题)
21.如图,在△ABC中,∠B=32°,∠C=48°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F,求∠ADF的度数.21*cnjy*com
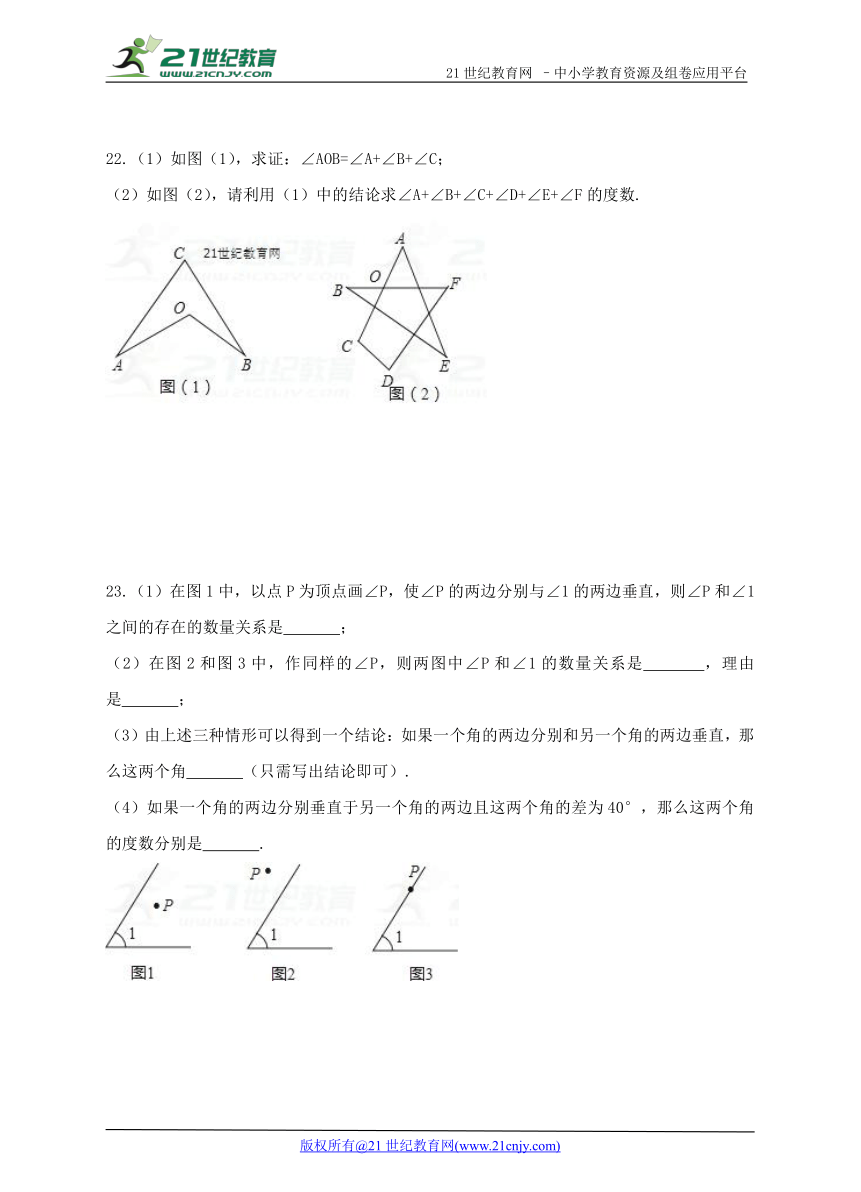
22.(1)如图(1),求证:∠AOB=∠A+∠B+∠C;
(2)如图(2),请利用(1)中的结论求∠A+∠B+∠C+∠D+∠E+∠F的度数.
23.(1)在图1中,以点P为顶点画∠P,使∠P的两边分别与∠1的两边垂直,则∠P和∠1之间的存在的数量关系是 ;
(2)在图2和图3中,作同样的∠P,则两图中∠P和∠1的数量关系是 ,理由是 ;
(3)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (只需写出结论即可).21世纪教育网版权所有
(4)如果一个角的两边分别垂直于另一个角的两边且这两个角的差为40°,那么这两个角的度数分别是 .
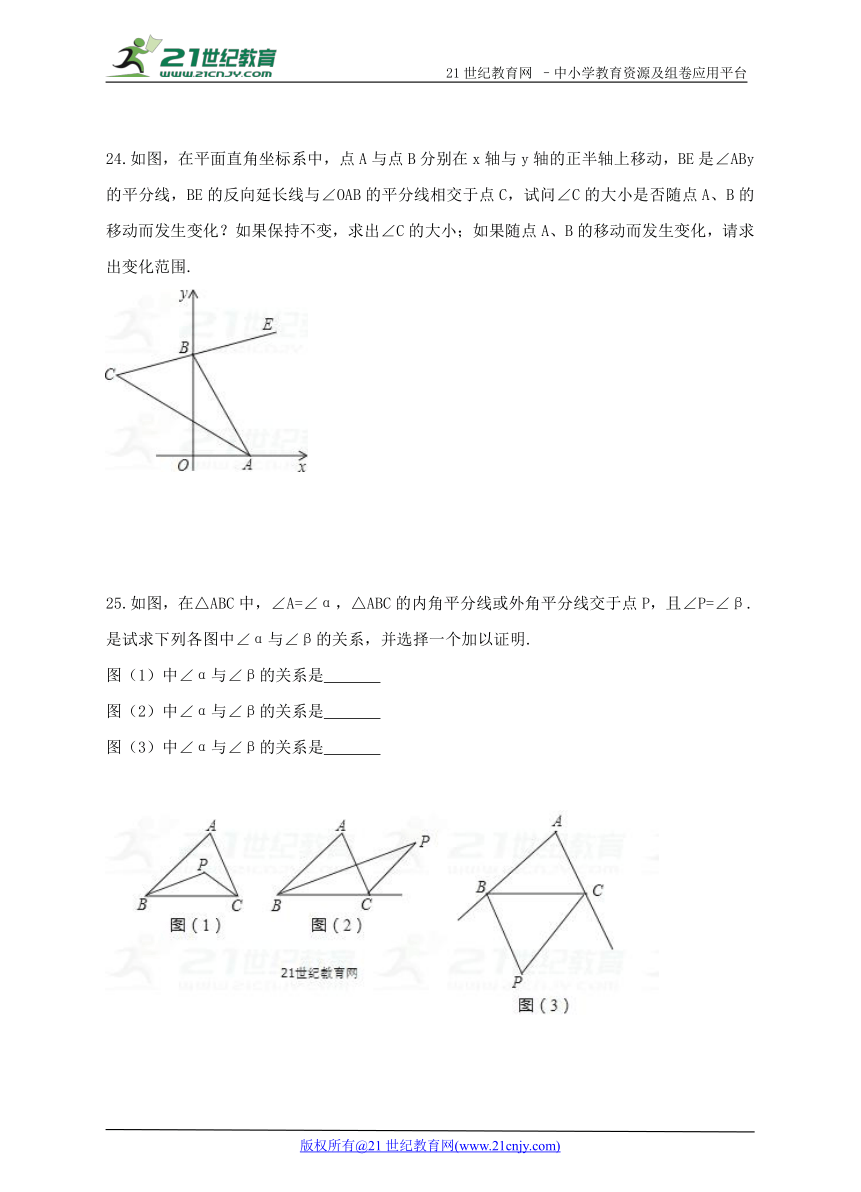
24.如图,在平面直角坐标系中,点A与点B分别在x轴与y轴的正半轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠C的大小是否随点A、B的移动而发生变化?如果保持不变,求出∠C的大小;如果随点A、B的移动而发生变化,请求出变化范围.21·世纪*教育网
25.如图,在△ABC中,∠A=∠α,△ABC的内角平分线或外角平分线交于点P,且∠P=∠β.是试求下列各图中∠α与∠β的关系,并选择一个加以证明.21*cnjy*com
图(1)中∠α与∠β的关系是
图(2)中∠α与∠β的关系是
图(3)中∠α与∠β的关系是
26.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠得到图 ②,填空:∠1+∠2 ∠B+∠C(填><=),当∠A=40°时,∠1+∠2+∠B+∠C= .【来源:21cnj*y.co*m】
(3)如图③是由图①的△ABC沿DE折叠得到的,猜想∠BDA+∠CEA与∠A的关系,并说明理由.
3B.【解答】解:设第三根木棒的长度为xcm,由三角形三边关系可得7﹣5<x<7+5,
即2<x<12,又x为偶数,∴x的值为4,6,8,10,共四种,故选B.
4C.【解答】解:分成四种情况:①4cm,6cm,8cm;②4cm,6cm,10cm;③4cm,8cm,10cm;④6cm,8cm,10cm,∵4+6=10,∴②不能够成三角形,故可以画出三角形的个数为3个.
5A.【解答】解:根据三角形的稳定性可固定窗户.故选A.
6C【解答】解:在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,
∴BD是△ABC的高,BE是△BMN的高,C故选CD是△BCD的高,故选C
7B.【解答】解:∠BDE+∠BED=180°﹣∠B,=180°﹣50°,=130°,
∠1+∠2=360°﹣(∠BDE+∠BED),=360°﹣130°,=230°.故选:B.
8D.【解答】解:A、三角形的角平分线是线段,不是射线,错误;
B、钝角三角形三条高,有两条在三角形外部,错误;
C、在钝角三角形中,该钝角的外角就比这个钝角小,错误;
D、因为A、B、C都错误,所以用排除法知D正确.
9A.【解答】解:∵∠B=60°,∴∠BAC+∠BCA=180°﹣60°=120°,
∴∠EAC+∠ACF=360°﹣120°=240°,∵AD、CD是外角平分线,
∴∠CAD+∠ACD=(∠EAC+∠ACF)=×240°=120°,
在△ACD中,∠D=180°﹣(∠CAD+∠ACD)=180°﹣120°=60°.故选A.
10A.【解答】解:以其中的三条线段为边组成三角形的有:2cm,3cm,4cm;2cm,4cm,5cm;3cm,4cm,5cm共有3种情况. www-2-1-cnjy-com
二.填空题(共10小题)
11. 35 度.
【解答】解:∵△ABC中,∠A=100°,∠C=45°,
∴∠B=180°﹣∠A﹣∠C=180°﹣100°﹣45°=35°.故答案为35.
∴∠AFD=∠AFG+∠DFG=∠AED﹣∠A﹣∠D=143°﹣23°﹣31°=89°≠90°.所以零件不合格.
14. 7 .
【解答】解:设第三边的长为x,根据三角形的三边关系,得7﹣2<x<7+2,即5<x<9,
又∵第三边长是奇数,∴x=7.故答案为7.
15. 0 .
【解答】解:∵a,b,c是一个三角形的三条边长,∴a﹣b+c>0,b﹣a﹣c<0,
∴|a﹣b+c|﹣|b﹣a﹣c|=a﹣b+c+b﹣a﹣c=0.故答案为:0.
16. 180 度.
【解答】解:∠AOD+∠COB=∠AOD+∠AOC+∠AOD+∠BOD=∠COD+∠AOB=90°+90°=180°.
17. 270° .
【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2=270°.故答案为:270°.
18. .
【解答】解:∵D是BC的中点,E是AD的中点,
∴S△ABD=S△ABC=3,S△ACD=S△BCE=3,S△BDE=S△ABD=,S△CDE=S△ACD=,21cnjy.com
∴S△BCE=S△BDE+S△CDE=+=3,∵F是CE的中点,∴S阴影=S△BCE=.故答案为:.
19. 20° .
【解答】解:∵∠EDC+∠C=∠AED,∠ADE=∠AED,∴∠C+∠EDC=∠ADE,
又∵∠B+∠BAD=∠ADC,∴∠B+40°=∠C+∠EDC+∠EDC,
∵∠B=∠C.∴2∠EDC=40°,∴∠EDC=20°.故答案为:20°.
20. 3° .
【解答】解:∠BA1C+∠A1BC=∠A1CD,2∠A1CD=∠ACD=∠BAC+∠ABC,
∴2(∠BA1C+∠A1BC)=∠BAC+∠ABC,2∠BA1C+2∠A1BC=∠BAC+∠ABC,
而2∠A1BC=∠ABC,∴2∠BA1C=∠BAC,
同理,可得2∠BA2C=∠BA1C,2∠BA3C=∠BA2C,2∠BA4C=∠BA3C,2∠BA5C=∠BA4C,
∴∠BA5C=∠BA4C=∠BA3C=∠BA2C=∠BA1C=∠BAC=96°÷32=3°,故∠A5=3°.
三.解答题(共6小题)
21.【解答】解:在△ABC中,∠B=32°,∠C=48°,∴∠BAC=180°﹣∠B﹣∠C=100°,
∵AE平分∠BAC,∴∠CAE=∠BAC=50°,∵AD⊥BC,∴∠CAD=90°﹣∠C=42°,
∴∠DAE=∠CAE﹣∠CAD=8°,∵DF⊥AE,∴∠ADF=90°﹣∠DAE=82°.
22.【解答】证明:(1)连接AB,如图(1)
由三角形的外角等于与它不相邻的两个内角的和,得∠1=∠B+∠F,∠2=∠A+∠E,
由四边形内角和得∠1+∠2+∠D+∠E=(4﹣2)×180°=360°.
则∠A+∠B+∠C+∠D+∠E+∠F=360°.
23.【解答】解:(1)∠P与∠1互补.
故答案为互补.
(2)∠P=∠1相等.理由:同角(或等角)的余角相等.
(3)相等或互补.
(4)由题意这两个角互补,不妨设这两个角分别为α、β.(α>β)
则解得
在△PBC中,∠BPC=180°﹣(∠PCB+∠PCB)=180°﹣(90°﹣α)=90°+α.
∴β=90°+α.故答案为:β=90°+α.
如图(2),结论:∠BPC=∠A.
证明如下:
∠P=∠1﹣∠2=(∠ACD﹣∠ABC)=∠A.∴β=α;
如图(3)∵BP、CP分别是△ABC两个外角∠CBD和∠BCE的平分线,
∴∠CBP=(∠A+∠ACB),∠BCP=(∠A+∠ABC),
∴∠BPC=180°﹣∠CBP﹣∠BCP=180°﹣∠A﹣(∠ABC+∠ACB),
∴∠P与∠A的关系是:∠P=180°﹣∠A﹣(∠ABC+∠ACB)=90°﹣α,
即β=90°﹣α.
26. 【解答】解:(1)根据三角形内角是180°,可知:∠1+∠2=180°﹣∠A,
∠B+∠C=180°﹣∠A,∴∠1+∠2=∠B+∠C;
(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,∴∠1+∠2=∠B+∠C;
当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°;
(3)如果∠A=30°,则∠BDA+∠CEA=360°﹣(∠B+∠C+∠1+∠2)=360°﹣300°=60°,
∴∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
八上数学第十一章培优提高 与三角形有关的线段和角
一.选择题(共10小题)
1.如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=50°,则∠BPC的度数是( )21·cn·jy·com
A.100 B.120 C.130 D.150
2.若一个三角形的两个内角的平分线所成的钝角为145°,则这个三角形的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.两根木棒分别为5cm和7cm,要选择第三根,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有( )2·1·c·n·j·y
A.3种 B.4种 C.5种 D.6种
4.以长为8cm、6cm、10cm、4cm的四条线段中的三条线段为边,可以画出三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短 C.N点确定一条直线 D.垂线段最短
6.如图所示,在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,则下列说法中,不正确的是( )【出处:21教育名师】
A.BD是△ABC的高 B.CD是△BCD的高 C.ME是△ABD的高 D.BE是△BMN的高
7.如图,已知△ABC中,∠B=50°,若沿图中虚线剪去∠B,则∠1+∠2等于( )
A.130° B.230° C.270° D.310°
8.下列说法正确的是( )
A.三角形的角平分线是射线
B.三角形的三条高一定在三角形内部
C.三角形的外角必大于每一个内角
D.三角形的一条中线把原三角形分成的两个小三角形面积相等
9.如图△ABC的两个外角的平分线交于点D,若∠B=60°,则∠D等于( )
A.60° B.80° C.65° D.30°
10.有5条线段,它们的长度分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长,可组成不同的三角形的个数为( )【版权所有:21教育】
A.3 B.4 C.5 D.6
二.填空题(共10小题)
11.如图,是一块三角形木板的残余部分,若量得∠A=100°,∠C=45°,则这块三角形木板另外一个角是 度.2-1-c-n-j-y
12.如图,△ABC中,AD平分∠BAC,AE是BC边上的高,若∠B=30°,∠C=70°,则∠DAE的度数等于 .www.21-cn-jy.com
13.某机器零件的横截面如图所示,按要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°,∠D=31°,∠AED=143°,请你帮他判断该零件是否合格 (填“合格”或“不合格”).21教育名师原创作品
14.已知三角形的两边长分别为2和7,第三边为奇数,则它第三边的长是 .
15.已知a,b,c是一个三角形的三条边长,则化简|a﹣b+c|﹣|b﹣a﹣c|= .
16.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOD+∠COB的度数为 .
17.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2= .
18.如图,在△ABC中,点D,E,F分别为边BC,AD,CE的中点,且S△ABC=6cm2,则S阴影= .
19.如图,在△ABC中,∠B=∠C,∠BAD=40°,∠ADE=∠AED,则∠CDE的度数为 .
20.如图△ABC中,∠A=96°,延长BC到D,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,以此类推,∠A4BC的平分线与∠A4CD的平分线交于点A5,则∠A5的大小是 .21教育网
三.解答题(共6小题)
21.如图,在△ABC中,∠B=32°,∠C=48°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F,求∠ADF的度数.21*cnjy*com
22.(1)如图(1),求证:∠AOB=∠A+∠B+∠C;
(2)如图(2),请利用(1)中的结论求∠A+∠B+∠C+∠D+∠E+∠F的度数.
23.(1)在图1中,以点P为顶点画∠P,使∠P的两边分别与∠1的两边垂直,则∠P和∠1之间的存在的数量关系是 ;
(2)在图2和图3中,作同样的∠P,则两图中∠P和∠1的数量关系是 ,理由是 ;
(3)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (只需写出结论即可).21世纪教育网版权所有
(4)如果一个角的两边分别垂直于另一个角的两边且这两个角的差为40°,那么这两个角的度数分别是 .
24.如图,在平面直角坐标系中,点A与点B分别在x轴与y轴的正半轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠C的大小是否随点A、B的移动而发生变化?如果保持不变,求出∠C的大小;如果随点A、B的移动而发生变化,请求出变化范围.21·世纪*教育网
25.如图,在△ABC中,∠A=∠α,△ABC的内角平分线或外角平分线交于点P,且∠P=∠β.是试求下列各图中∠α与∠β的关系,并选择一个加以证明.21*cnjy*com
图(1)中∠α与∠β的关系是
图(2)中∠α与∠β的关系是
图(3)中∠α与∠β的关系是
26.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠得到图 ②,填空:∠1+∠2 ∠B+∠C(填><=),当∠A=40°时,∠1+∠2+∠B+∠C= .【来源:21cnj*y.co*m】
(3)如图③是由图①的△ABC沿DE折叠得到的,猜想∠BDA+∠CEA与∠A的关系,并说明理由.
3B.【解答】解:设第三根木棒的长度为xcm,由三角形三边关系可得7﹣5<x<7+5,
即2<x<12,又x为偶数,∴x的值为4,6,8,10,共四种,故选B.
4C.【解答】解:分成四种情况:①4cm,6cm,8cm;②4cm,6cm,10cm;③4cm,8cm,10cm;④6cm,8cm,10cm,∵4+6=10,∴②不能够成三角形,故可以画出三角形的个数为3个.
5A.【解答】解:根据三角形的稳定性可固定窗户.故选A.
6C【解答】解:在△ABC中,MN∥AC,BD⊥AC于点D,交MN于点E,
∴BD是△ABC的高,BE是△BMN的高,C故选CD是△BCD的高,故选C
7B.【解答】解:∠BDE+∠BED=180°﹣∠B,=180°﹣50°,=130°,
∠1+∠2=360°﹣(∠BDE+∠BED),=360°﹣130°,=230°.故选:B.
8D.【解答】解:A、三角形的角平分线是线段,不是射线,错误;
B、钝角三角形三条高,有两条在三角形外部,错误;
C、在钝角三角形中,该钝角的外角就比这个钝角小,错误;
D、因为A、B、C都错误,所以用排除法知D正确.
9A.【解答】解:∵∠B=60°,∴∠BAC+∠BCA=180°﹣60°=120°,
∴∠EAC+∠ACF=360°﹣120°=240°,∵AD、CD是外角平分线,
∴∠CAD+∠ACD=(∠EAC+∠ACF)=×240°=120°,
在△ACD中,∠D=180°﹣(∠CAD+∠ACD)=180°﹣120°=60°.故选A.
10A.【解答】解:以其中的三条线段为边组成三角形的有:2cm,3cm,4cm;2cm,4cm,5cm;3cm,4cm,5cm共有3种情况. www-2-1-cnjy-com
二.填空题(共10小题)
11. 35 度.
【解答】解:∵△ABC中,∠A=100°,∠C=45°,
∴∠B=180°﹣∠A﹣∠C=180°﹣100°﹣45°=35°.故答案为35.
∴∠AFD=∠AFG+∠DFG=∠AED﹣∠A﹣∠D=143°﹣23°﹣31°=89°≠90°.所以零件不合格.
14. 7 .
【解答】解:设第三边的长为x,根据三角形的三边关系,得7﹣2<x<7+2,即5<x<9,
又∵第三边长是奇数,∴x=7.故答案为7.
15. 0 .
【解答】解:∵a,b,c是一个三角形的三条边长,∴a﹣b+c>0,b﹣a﹣c<0,
∴|a﹣b+c|﹣|b﹣a﹣c|=a﹣b+c+b﹣a﹣c=0.故答案为:0.
16. 180 度.
【解答】解:∠AOD+∠COB=∠AOD+∠AOC+∠AOD+∠BOD=∠COD+∠AOB=90°+90°=180°.
17. 270° .
【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2=270°.故答案为:270°.
18. .
【解答】解:∵D是BC的中点,E是AD的中点,
∴S△ABD=S△ABC=3,S△ACD=S△BCE=3,S△BDE=S△ABD=,S△CDE=S△ACD=,21cnjy.com
∴S△BCE=S△BDE+S△CDE=+=3,∵F是CE的中点,∴S阴影=S△BCE=.故答案为:.
19. 20° .
【解答】解:∵∠EDC+∠C=∠AED,∠ADE=∠AED,∴∠C+∠EDC=∠ADE,
又∵∠B+∠BAD=∠ADC,∴∠B+40°=∠C+∠EDC+∠EDC,
∵∠B=∠C.∴2∠EDC=40°,∴∠EDC=20°.故答案为:20°.
20. 3° .
【解答】解:∠BA1C+∠A1BC=∠A1CD,2∠A1CD=∠ACD=∠BAC+∠ABC,
∴2(∠BA1C+∠A1BC)=∠BAC+∠ABC,2∠BA1C+2∠A1BC=∠BAC+∠ABC,
而2∠A1BC=∠ABC,∴2∠BA1C=∠BAC,
同理,可得2∠BA2C=∠BA1C,2∠BA3C=∠BA2C,2∠BA4C=∠BA3C,2∠BA5C=∠BA4C,
∴∠BA5C=∠BA4C=∠BA3C=∠BA2C=∠BA1C=∠BAC=96°÷32=3°,故∠A5=3°.
三.解答题(共6小题)
21.【解答】解:在△ABC中,∠B=32°,∠C=48°,∴∠BAC=180°﹣∠B﹣∠C=100°,
∵AE平分∠BAC,∴∠CAE=∠BAC=50°,∵AD⊥BC,∴∠CAD=90°﹣∠C=42°,
∴∠DAE=∠CAE﹣∠CAD=8°,∵DF⊥AE,∴∠ADF=90°﹣∠DAE=82°.
22.【解答】证明:(1)连接AB,如图(1)
由三角形的外角等于与它不相邻的两个内角的和,得∠1=∠B+∠F,∠2=∠A+∠E,
由四边形内角和得∠1+∠2+∠D+∠E=(4﹣2)×180°=360°.
则∠A+∠B+∠C+∠D+∠E+∠F=360°.
23.【解答】解:(1)∠P与∠1互补.
故答案为互补.
(2)∠P=∠1相等.理由:同角(或等角)的余角相等.
(3)相等或互补.
(4)由题意这两个角互补,不妨设这两个角分别为α、β.(α>β)
则解得
在△PBC中,∠BPC=180°﹣(∠PCB+∠PCB)=180°﹣(90°﹣α)=90°+α.
∴β=90°+α.故答案为:β=90°+α.
如图(2),结论:∠BPC=∠A.
证明如下:
∠P=∠1﹣∠2=(∠ACD﹣∠ABC)=∠A.∴β=α;
如图(3)∵BP、CP分别是△ABC两个外角∠CBD和∠BCE的平分线,
∴∠CBP=(∠A+∠ACB),∠BCP=(∠A+∠ABC),
∴∠BPC=180°﹣∠CBP﹣∠BCP=180°﹣∠A﹣(∠ABC+∠ACB),
∴∠P与∠A的关系是:∠P=180°﹣∠A﹣(∠ABC+∠ACB)=90°﹣α,
即β=90°﹣α.
26. 【解答】解:(1)根据三角形内角是180°,可知:∠1+∠2=180°﹣∠A,
∠B+∠C=180°﹣∠A,∴∠1+∠2=∠B+∠C;
(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,∴∠1+∠2=∠B+∠C;
当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°;
(3)如果∠A=30°,则∠BDA+∠CEA=360°﹣(∠B+∠C+∠1+∠2)=360°﹣300°=60°,
∴∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
