2017年秋九年级上《24.1.2垂直于弦的直径》同步练习含答案
文档属性
| 名称 | 2017年秋九年级上《24.1.2垂直于弦的直径》同步练习含答案 | 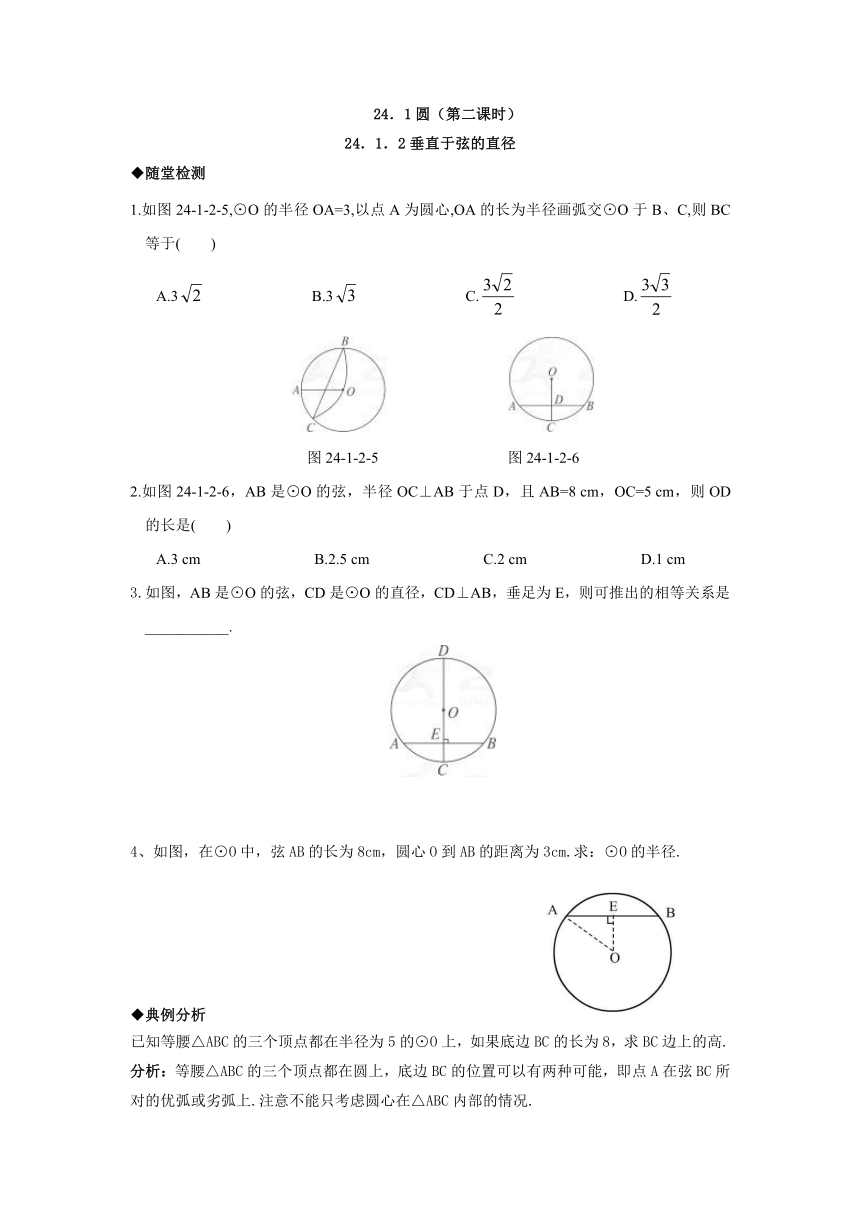 | |
| 格式 | zip | ||
| 文件大小 | 223.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-04 11:02:38 | ||
图片预览


文档简介
24.1圆(第二课时)
24.1.2垂直于弦的直径
◆随堂检测
1.如图24-1-2-5,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC等于(
)
A.3
B.3
C.
D.
图24-1-2-5
图24-1-2-6
2.如图24-1-2-6,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8
cm,OC=5
cm,则OD的长是(
)
A.3
cm
B.2.5
cm
C.2
cm
D.1
cm
3.如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,则可推出的相等关系是___________.
4、如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm.求:⊙O的半径.
◆典例分析
已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,求BC边上的高.
分析:等腰△ABC的三个顶点都在圆上,底边BC的位置可以有两种可能,即点A在弦BC所对的优弧或劣弧上.注意不能只考虑圆心在△ABC内部的情况.
解:作AD⊥BC,则AD即为BC边上的高.设圆心O到BC的距离为d,则依据垂径定理得BC=4,d2=52-42=9,所以d=3.
当圆心在三角形内部时BC边上的高为5+3=8;
当圆心在三角形内外部时BC边上的高为5-3=2.
◆课下作业
●拓展提高
1、如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为(
)
A、
B、
C、
D、
2、如图,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是(
)
A、AB⊥CD
B、∠AOB=4∠ACD
C、
D、PO=PD
3、如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
4、如图,一条公路的转弯处是一段圆弦(即图中,点O是的圆心,其中CD=600m,E为上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
5、如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
●体验中考
1、(2009年)如图,一条公路的转变处是一段圆弧(图中的),点是这段弧的圆心,是上一点,,垂足为,则这段弯路的半径是_________m.
2、(2009年)用圆规、直尺作图,不写作法,但要保留作图痕迹.
为美化校园,学校准备在如图所示的三角形()空地上修建一个面积最大的圆形花坛,请在图中画出这个圆形花坛.
参考答案:
◆随堂检测
1、B.
2、A.
3、答案:OC=OD、AE=BE、弧AC=弧BC、弧AD=弧BD
4、解:过点O作OE⊥AB于E.∵弦AB的长为8cm,圆心O到AB的距离OE=3cm,∴依据垂径定理得AE=4cm,在Rt△AOE中,由勾股定理得OA=5cm.即⊙O的半径为5cm.
◆课下作业
●拓展提高
1、.
2、D.
解:连结OA、OC,在Rt△OCG中,,
Rt△,
在Rt△OAE中,,∴解得,∴.
4、解:由图可得,在Rt△OCF中,,解得.
∴这段弯路的半径是.
5、解:过点O作OH⊥CD,垂足为H,
∵AE=2,EB=6,∴OA=OB=4,OE=2,
∵∠DEB=30°,∴OH=1,HD=,∴CD=.
●体验中考
1、250.
依据垂径定理和勾股定理可得.
2、解:先画出两条角平分线,其交点即为圆心;再确定半径;最后画出圆形花坛.
O
C
B
A
C
B
A
O
A
O
C
B
D
5
24.1.2垂直于弦的直径
◆随堂检测
1.如图24-1-2-5,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC等于(
)
A.3
B.3
C.
D.
图24-1-2-5
图24-1-2-6
2.如图24-1-2-6,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8
cm,OC=5
cm,则OD的长是(
)
A.3
cm
B.2.5
cm
C.2
cm
D.1
cm
3.如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,则可推出的相等关系是___________.
4、如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm.求:⊙O的半径.
◆典例分析
已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,求BC边上的高.
分析:等腰△ABC的三个顶点都在圆上,底边BC的位置可以有两种可能,即点A在弦BC所对的优弧或劣弧上.注意不能只考虑圆心在△ABC内部的情况.
解:作AD⊥BC,则AD即为BC边上的高.设圆心O到BC的距离为d,则依据垂径定理得BC=4,d2=52-42=9,所以d=3.
当圆心在三角形内部时BC边上的高为5+3=8;
当圆心在三角形内外部时BC边上的高为5-3=2.
◆课下作业
●拓展提高
1、如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为(
)
A、
B、
C、
D、
2、如图,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是(
)
A、AB⊥CD
B、∠AOB=4∠ACD
C、
D、PO=PD
3、如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
4、如图,一条公路的转弯处是一段圆弦(即图中,点O是的圆心,其中CD=600m,E为上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
5、如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
●体验中考
1、(2009年)如图,一条公路的转变处是一段圆弧(图中的),点是这段弧的圆心,是上一点,,垂足为,则这段弯路的半径是_________m.
2、(2009年)用圆规、直尺作图,不写作法,但要保留作图痕迹.
为美化校园,学校准备在如图所示的三角形()空地上修建一个面积最大的圆形花坛,请在图中画出这个圆形花坛.
参考答案:
◆随堂检测
1、B.
2、A.
3、答案:OC=OD、AE=BE、弧AC=弧BC、弧AD=弧BD
4、解:过点O作OE⊥AB于E.∵弦AB的长为8cm,圆心O到AB的距离OE=3cm,∴依据垂径定理得AE=4cm,在Rt△AOE中,由勾股定理得OA=5cm.即⊙O的半径为5cm.
◆课下作业
●拓展提高
1、.
2、D.
解:连结OA、OC,在Rt△OCG中,,
Rt△,
在Rt△OAE中,,∴解得,∴.
4、解:由图可得,在Rt△OCF中,,解得.
∴这段弯路的半径是.
5、解:过点O作OH⊥CD,垂足为H,
∵AE=2,EB=6,∴OA=OB=4,OE=2,
∵∠DEB=30°,∴OH=1,HD=,∴CD=.
●体验中考
1、250.
依据垂径定理和勾股定理可得.
2、解:先画出两条角平分线,其交点即为圆心;再确定半径;最后画出圆形花坛.
O
C
B
A
C
B
A
O
A
O
C
B
D
5
同课章节目录
