2017—2018学年数学(华师版)九年级上册检测题:第24章 解直角三角形检测题(含答案)
文档属性
| 名称 | 2017—2018学年数学(华师版)九年级上册检测题:第24章 解直角三角形检测题(含答案) | 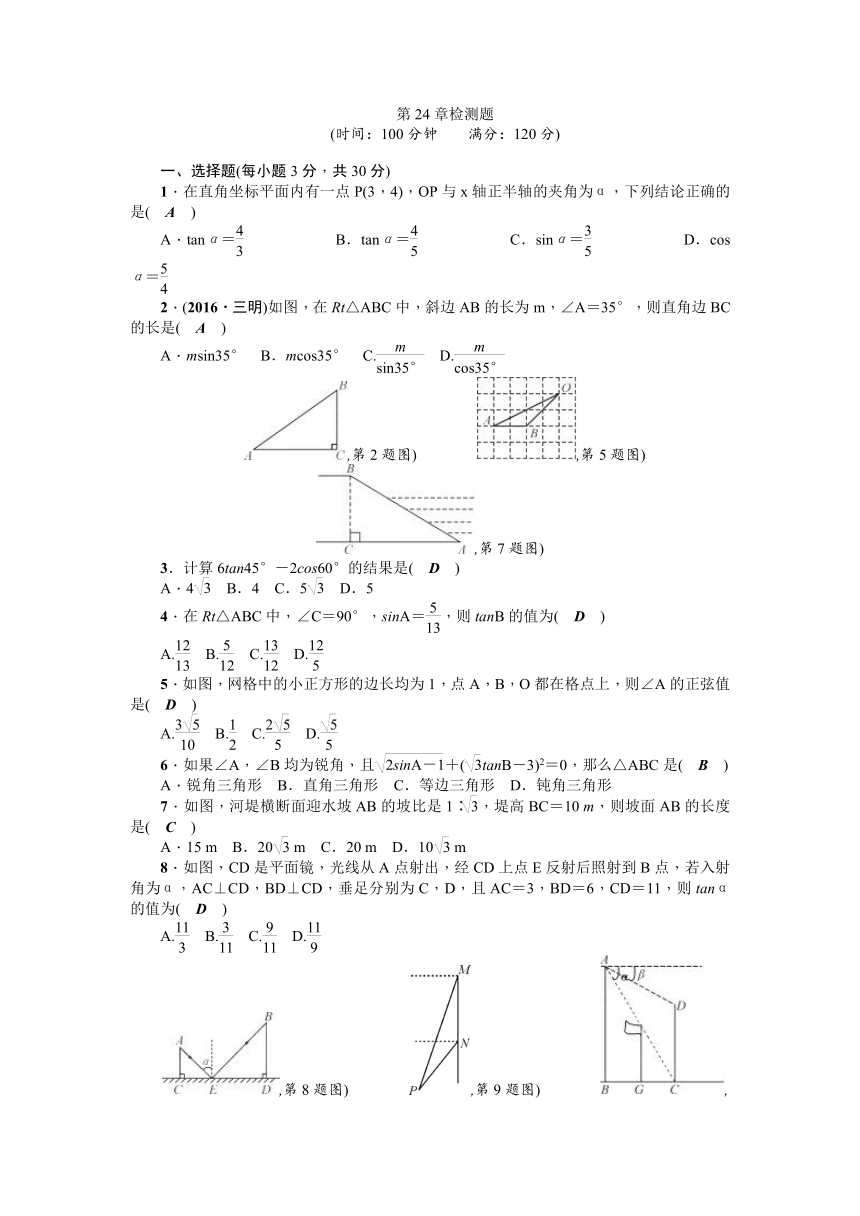 | |
| 格式 | zip | ||
| 文件大小 | 254.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-04 05:10:12 | ||
图片预览


文档简介
第24章检测题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.在直角坐标平面内有一点P(3,4),OP与x轴正半轴的夹角为α,下列结论正确的是( A )
A.tanα= B.tanα= C.sinα= D.cosα=
2.(2016·三明)如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( A )
A.msin35°
B.mcos35°
C.
D.
,第2题图) ,第5题图) ,第7题图)
3.计算6tan45°-2cos60°的结果是( D )
A.4
B.4
C.5
D.5
4.在Rt△ABC中,∠C=90°,sinA=,则tanB的值为( D )
A.
B.
C.
D.
5.如图,网格中的小正方形的边长均为1,点A,B,O都在格点上,则∠A的正弦值是( D )
A.
B.
C.
D.
6.如果∠A,∠B均为锐角,且+(tanB-3)2=0,那么△ABC是( B )
A.锐角三角形
B.直角三角形
C.等边三角形
D.钝角三角形
7.如图,河堤横断面迎水坡AB的坡比是1∶,堤高BC=10
m,则坡面AB的长度是( C )
A.15
m
B.20
m
C.20
m
D.10
m
8.如图,CD是平面镜,光线从A点射出,经CD上点E反射后照射到B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值为( D )
A.
B.
C.
D.
,第8题图) ,第9题图) ,第10题图)
9.(2016·泰安)如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°≈0.9272,sin46°≈0.7193,sin22°≈0.3746,sin44°≈0.6947)( B )
A.22.48海里
B.41.68海里
C.43.16海里
D.55.63海里
10.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( A )
A.20米
B.10
米
C.15
米
D.5
米
二、填空题(每小题3分,共24分)
11.计算:tan45°-(-1)0=____.
12.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinA的值是____.
13.如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为__100__米.
,第12题图) ,第13题图) ,第14题图)
14.如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=6
cm,sinA=,则菱形ABCD的面积是__60__cm2.
15.将一副三角尺如图所示叠放在一起,则的值是____.
16.如图,△ABC的顶点A,C的坐标分别是(0,4),(3,0),且∠ACB=90°,∠B=30°,则顶点B的坐标是__(3+4,3)__.
,第15题图) ,第16题图) ,第18题图)
17.在△ABC中,AB=4,BC=3,∠BAC=30°,则△ABC的面积为__2+或2-__.
18.为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5
米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出__17__个这样的停车位.(≈1.4)
点拨:如图,BC=2.2×sin45°≈1.54,CE=5×sin45°≈3.5,BE=BC+CE≈5.04,EF=2.2÷sin45°≈3.14,(56-5.04)÷3.14+1≈16+1=17(个),故这个路段最多可以划出17个这样的停车位
三、解答题(共66分)
19.(8分)计算:
(1)(-)0+()-1·-|tan45°-|;
解:2+
(2)sin45°+cos230°-+2sin60°.
解:1+
20.(8分)(2016·呼伦贝尔)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
解:
21.(9分)如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E,若AD=1,AB=2,求CE的长.
解:过点A作AH⊥BC于点H,则AD=HC=1,在△ABH中,BH=AB·cos30°=3,∴BC=BH+HC=4,∵CE⊥AB,∴CE=BC·sin30°=2
22.(9分)(2016·青岛)如图,AB是长为10
m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度.(结果保留整数,参考数据:sin37°≈,tan37°≈,sin65°≈,tan65°≈)
解:作BF⊥AE于点F,则BF=DE,在Rt△ABF中,sin∠BAF=,则BF=AB·sin∠BAF=10×=6(m),在Rt△CDB中,tan∠CBD=,则CD=BD·tan65°=10×≈21(m),∴CE=DE+CD=27
m,答:大楼CE的高度约为27m
23.(10分)图①,②分别是某型号跑步机的实物图与示意图,已知踏板CD长为1.6
m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8
m,∠ACD为80°,求跑步机手柄的一端A的高度h.(精确到0.1
m,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
解:过C点作FG⊥AB于点F,交DE于点G.∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,∴∠ACF=90°+12°-80°=22°,∴∠CAF=68°,在Rt△ACF中,CF=AC·sin∠CAF≈0.744,在Rt△CDG中,CG=CD·sin∠CDE≈0.336,∴FG=FC+CG≈1.1,故跑步机手柄的一端A的高度约为1.1
m
24.(10分)(2016·鄂州)为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A,B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60(+)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(-)海里.
(1)分别求出A与C及B与C的距离AC,BC;(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?(参考数据:≈1.41,≈1.73,≈2.45)
解:(1)过点C作CE⊥AB于点E,可得∠CBD=45°,∠CAD=60°,设CE=x,在Rt△CAE中,AE=CE·tan30°=x,在Rt△BCE中,BE=CE=x,∵AB=60(+)海里,∴x+x=60(+),解得x=60,则AC=x=120,BC=x=120,答:A与C的距离为120海里,B与C的距离为120海里 (2)过点D作DF⊥AC于点F,在△ADF中,∵AD=120(-),∠CAD=60°,∴DF=ADsin60°=180-60≈106.8>100,故海监船沿AC前往C处盘查,无触礁的危险
25.(12分)如图,已知斜坡AB长60米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE.
(1)若修建的斜坡BE的坡比为∶1,求休闲平台DE的长是多少米?
(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°,点B,C,A,G,H在同一个平面内,点C,A,G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
解:(1)∵FM∥CG,∴∠BDF=∠BAC=45°,∵斜坡AB长60,D是AB的中点,∴BD=30,在△BDF中,DF=BD·cos∠BDF
=30,BF=DF=30,∵斜坡BE的坡比为∶1,∴=,∴EF=10,∴DE=DF-EF=30-10,即休闲平台DE的长是(30-10)米 (2)设GH=x米,则MH=GH-GM=x-30,DM=AG+AP=33+30=63,在Rt△DMH中,tan30°=,即=,解得x=30+21,则建筑物GH的高为(30+21)米
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.在直角坐标平面内有一点P(3,4),OP与x轴正半轴的夹角为α,下列结论正确的是( A )
A.tanα= B.tanα= C.sinα= D.cosα=
2.(2016·三明)如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( A )
A.msin35°
B.mcos35°
C.
D.
,第2题图) ,第5题图) ,第7题图)
3.计算6tan45°-2cos60°的结果是( D )
A.4
B.4
C.5
D.5
4.在Rt△ABC中,∠C=90°,sinA=,则tanB的值为( D )
A.
B.
C.
D.
5.如图,网格中的小正方形的边长均为1,点A,B,O都在格点上,则∠A的正弦值是( D )
A.
B.
C.
D.
6.如果∠A,∠B均为锐角,且+(tanB-3)2=0,那么△ABC是( B )
A.锐角三角形
B.直角三角形
C.等边三角形
D.钝角三角形
7.如图,河堤横断面迎水坡AB的坡比是1∶,堤高BC=10
m,则坡面AB的长度是( C )
A.15
m
B.20
m
C.20
m
D.10
m
8.如图,CD是平面镜,光线从A点射出,经CD上点E反射后照射到B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值为( D )
A.
B.
C.
D.
,第8题图) ,第9题图) ,第10题图)
9.(2016·泰安)如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°≈0.9272,sin46°≈0.7193,sin22°≈0.3746,sin44°≈0.6947)( B )
A.22.48海里
B.41.68海里
C.43.16海里
D.55.63海里
10.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( A )
A.20米
B.10
米
C.15
米
D.5
米
二、填空题(每小题3分,共24分)
11.计算:tan45°-(-1)0=____.
12.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinA的值是____.
13.如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为__100__米.
,第12题图) ,第13题图) ,第14题图)
14.如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=6
cm,sinA=,则菱形ABCD的面积是__60__cm2.
15.将一副三角尺如图所示叠放在一起,则的值是____.
16.如图,△ABC的顶点A,C的坐标分别是(0,4),(3,0),且∠ACB=90°,∠B=30°,则顶点B的坐标是__(3+4,3)__.
,第15题图) ,第16题图) ,第18题图)
17.在△ABC中,AB=4,BC=3,∠BAC=30°,则△ABC的面积为__2+或2-__.
18.为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5
米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出__17__个这样的停车位.(≈1.4)
点拨:如图,BC=2.2×sin45°≈1.54,CE=5×sin45°≈3.5,BE=BC+CE≈5.04,EF=2.2÷sin45°≈3.14,(56-5.04)÷3.14+1≈16+1=17(个),故这个路段最多可以划出17个这样的停车位
三、解答题(共66分)
19.(8分)计算:
(1)(-)0+()-1·-|tan45°-|;
解:2+
(2)sin45°+cos230°-+2sin60°.
解:1+
20.(8分)(2016·呼伦贝尔)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
解:
21.(9分)如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E,若AD=1,AB=2,求CE的长.
解:过点A作AH⊥BC于点H,则AD=HC=1,在△ABH中,BH=AB·cos30°=3,∴BC=BH+HC=4,∵CE⊥AB,∴CE=BC·sin30°=2
22.(9分)(2016·青岛)如图,AB是长为10
m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度.(结果保留整数,参考数据:sin37°≈,tan37°≈,sin65°≈,tan65°≈)
解:作BF⊥AE于点F,则BF=DE,在Rt△ABF中,sin∠BAF=,则BF=AB·sin∠BAF=10×=6(m),在Rt△CDB中,tan∠CBD=,则CD=BD·tan65°=10×≈21(m),∴CE=DE+CD=27
m,答:大楼CE的高度约为27m
23.(10分)图①,②分别是某型号跑步机的实物图与示意图,已知踏板CD长为1.6
m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8
m,∠ACD为80°,求跑步机手柄的一端A的高度h.(精确到0.1
m,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
解:过C点作FG⊥AB于点F,交DE于点G.∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,∴∠ACF=90°+12°-80°=22°,∴∠CAF=68°,在Rt△ACF中,CF=AC·sin∠CAF≈0.744,在Rt△CDG中,CG=CD·sin∠CDE≈0.336,∴FG=FC+CG≈1.1,故跑步机手柄的一端A的高度约为1.1
m
24.(10分)(2016·鄂州)为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A,B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60(+)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(-)海里.
(1)分别求出A与C及B与C的距离AC,BC;(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?(参考数据:≈1.41,≈1.73,≈2.45)
解:(1)过点C作CE⊥AB于点E,可得∠CBD=45°,∠CAD=60°,设CE=x,在Rt△CAE中,AE=CE·tan30°=x,在Rt△BCE中,BE=CE=x,∵AB=60(+)海里,∴x+x=60(+),解得x=60,则AC=x=120,BC=x=120,答:A与C的距离为120海里,B与C的距离为120海里 (2)过点D作DF⊥AC于点F,在△ADF中,∵AD=120(-),∠CAD=60°,∴DF=ADsin60°=180-60≈106.8>100,故海监船沿AC前往C处盘查,无触礁的危险
25.(12分)如图,已知斜坡AB长60米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE.
(1)若修建的斜坡BE的坡比为∶1,求休闲平台DE的长是多少米?
(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°,点B,C,A,G,H在同一个平面内,点C,A,G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
解:(1)∵FM∥CG,∴∠BDF=∠BAC=45°,∵斜坡AB长60,D是AB的中点,∴BD=30,在△BDF中,DF=BD·cos∠BDF
=30,BF=DF=30,∵斜坡BE的坡比为∶1,∴=,∴EF=10,∴DE=DF-EF=30-10,即休闲平台DE的长是(30-10)米 (2)设GH=x米,则MH=GH-GM=x-30,DM=AG+AP=33+30=63,在Rt△DMH中,tan30°=,即=,解得x=30+21,则建筑物GH的高为(30+21)米
