11.3多边形及其内角和 课件
图片预览







文档简介
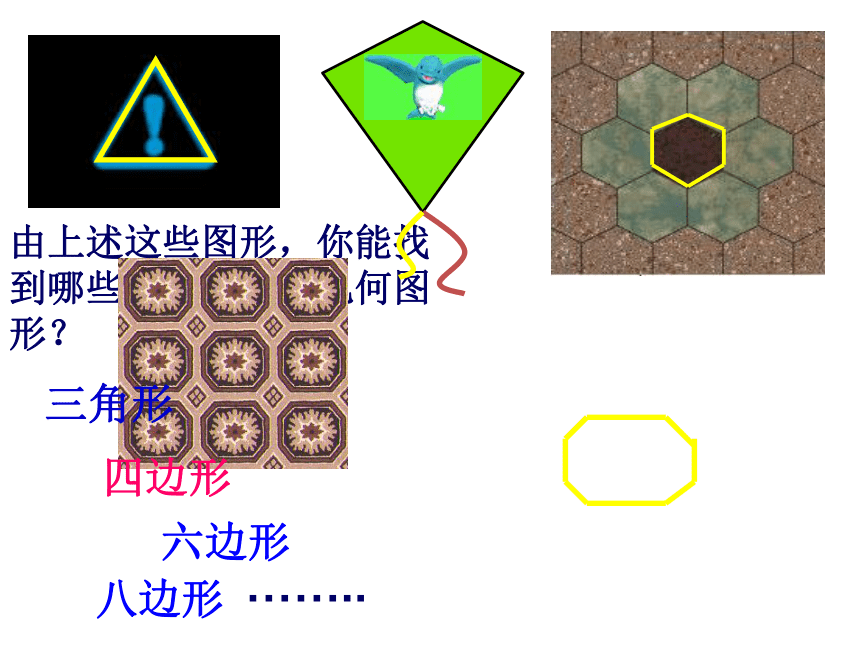
课件35张PPT。多边形及其内角和由上述这些图形,你能找到哪些我们熟习的几何图形?三角形 四边形 六边形 八边形……..三角形的定义: 在同一平面内,由不在同一条直线上的三条线段首尾顺次相接所组成的图形。四边形的定义: 在同一平面内,由不在同一条直线上的四条线段首尾顺次相接所组成的图形。……五边形六边形七边形多边形的定义: 在同一平面内,由不在同一条直线上的一些线段首尾顺次相接所组成的(封闭)图形。
下定义 多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。 如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。 注意:n所代表的数字必须是汉字中的数字,如三角形,六边形,十边形等等,但当问题问这个多边形有多少条边时,我们可以用阿拉伯数字说明这个n边形有3条边,4条边等。根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角边顶点内角外角对角线组成多边形的线段叫做多边形的边相邻两边的交点叫做多边形的顶点相邻两边的夹角叫做多边形的内角多边形的边与它相邻的延长组成的角叫做多边形的外角连接多边形不相邻的两个顶点的线段叫做多边形的对角线想一想三角形有对角线吗?为什么?没有,因为三角形只有三个顶点,而这三个顶点是两两相邻的,它没有不相邻的顶点,所以三角形没有对角线。回想三角形的表示方法,这个多边形应该如何表示?首先给每个顶点标上一个大写字母,然后写出这个图形是几边形,最后再以一个字母为起点,沿顺时针或逆时针方向将字母按顺序写出。如四边形ABCD,五边形ABCDE,
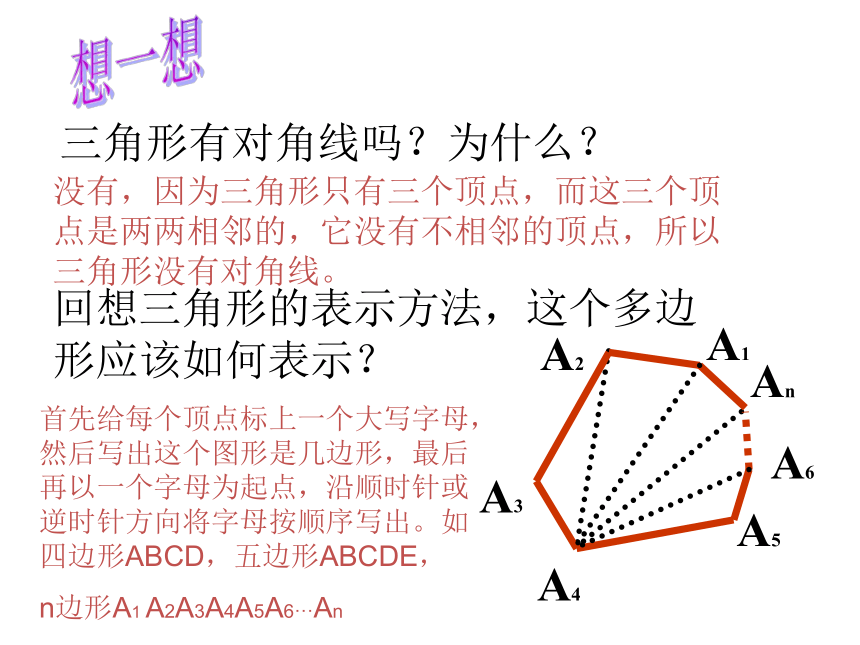
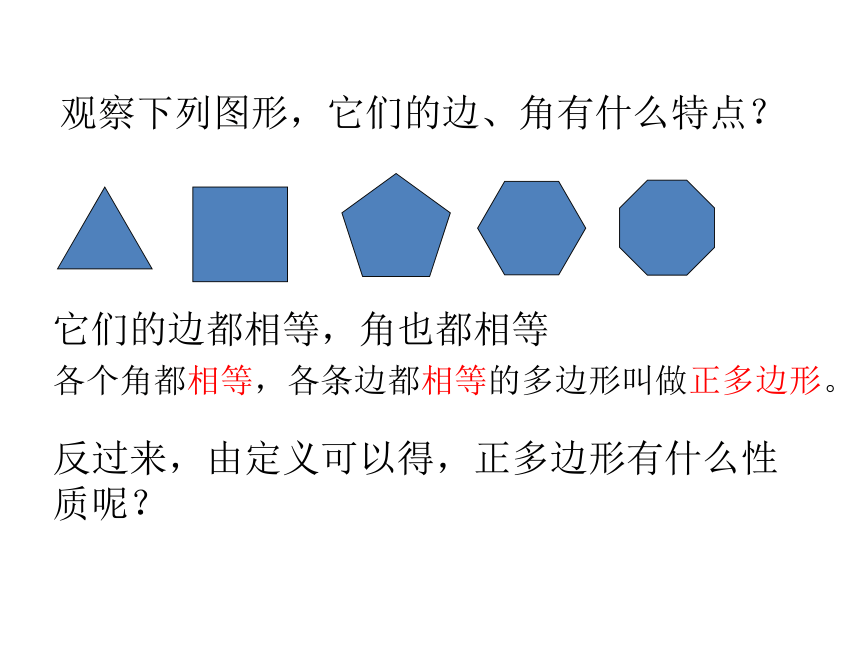
n边形A1 A2A3A4A5A6···An A3 A4 A1 An A6 A5如图所示,观察两个图形,找出相同点和不同点如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形如果整个多边形不在这条直线的同一侧,那么这个多边形就是凹多边形另外,根据多边形的内角和是否大于180°,我们也可以区分这两种多边形。而中学阶段我们一般说的多边形都是凸多边形。观察下列图形,它们的边、角有什么特点?它们的边都相等,角也都相等各个角都相等,各条边都相等的多边形叫做正多边形。反过来,由定义可以得,正多边形有什么性质呢?练一练1、填空题
(1)连接多边形( )的线段,叫做多边形的多角形。
(2)多边形的任何( )所在的直线,整个多边形都在这条直线的( ),这样的多边形叫做凸多边形 。
(3)各个角( ),各条边( )的多边形,叫做正多边形。
(4)一个n边形有( )条边, ( )个顶点, ( )个内角, ( )个外角。
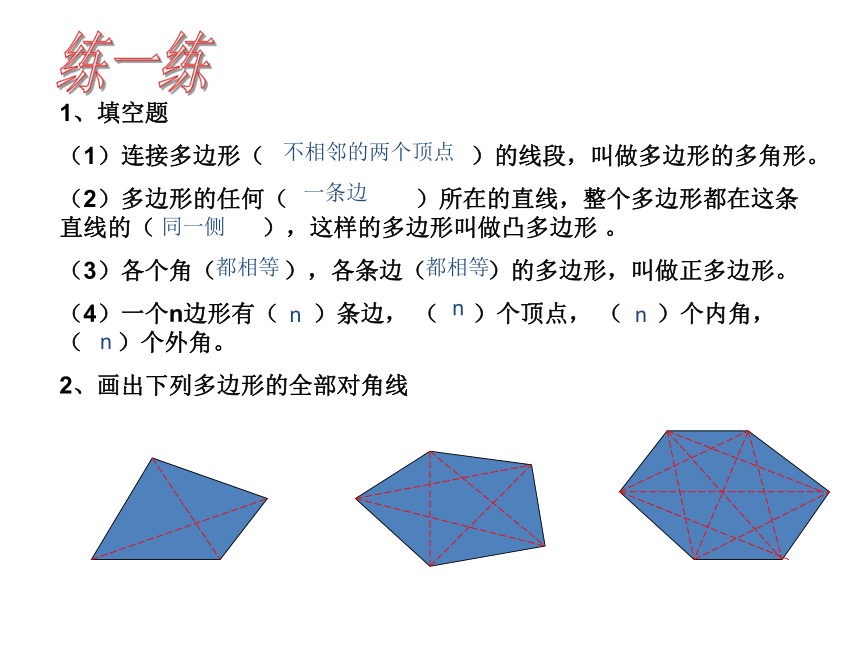
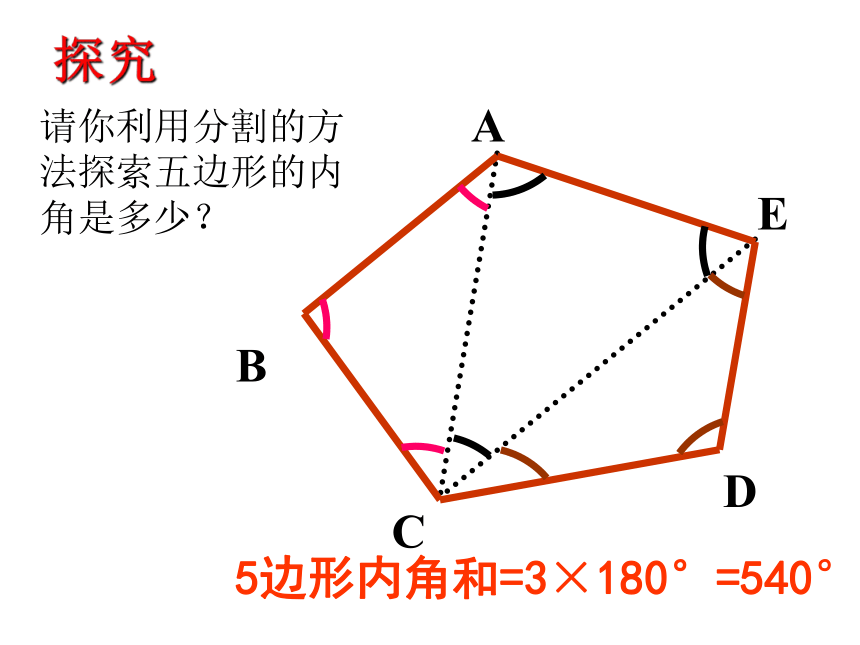
2、画出下列多边形的全部对角线不相邻的两个顶点一条边同一侧都相等都相等nnnn三角形的内角和是180°,那么四边形的内角和是多少呢?五边形呢?你是如何得到这个结论的?合作学习 B ACDE探究5边形内角和=3×180°=540°请你利用分割的方法探索五边形的内角是多少?E
ABCDO方法2180°× 5 – 360°= 540°180°× 5=900°?五边形内角和540°??把一个五边形分成几个三角形,还有其他的分法吗?ABCDEF180° × 4 – 180° = 540°方法3选择同一种方法分别求出任意六边形、七边形、八边形的内角和等于多少度?你能写出任意n边形的内角和吗?从五边形的一个顶点出发,可以引( )条对角线,他们将五边形分为多少个三角形,五边形的内角和等于180°×( )。从六边形的一个顶点出发,可以引( )条对角线,他们将六边形分为多少个三角形,六边形的内角和等于180°×( )。从七边形的一个顶点出发,可以引( )条对角线,他们将七边形分为多少个三角形,七边形的内角和等于180°×( )。我们是怎样求多边形内 角和的?就是从多边形的一个顶点出发,能引几条对角线把一个多边形分成几个三角形。总结:n边形内角和公式n边形内角和=(n-2) ·180°三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)合作学习请探索任意一个多边形的内角和与外角和的规律.………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°从上表中得到了什么结论?结论:n边形的内角和为:
(n-2)×180°(n≥3).n边形从一个顶点出发的对角线有(n-3)条(n≥3)练一练: (2)已知一个多边形的内角和为720o ,则这个多边形是______边形6 (3)在五边形ABCDE中,若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______80o(1)求十边形的内角和的度数。 解:(10-2)×180°=8 ×180°=1440°答:十边形的内角和是1440° 过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.3、填空(求边数)
1、已知一个多边形的内角和为1080°,则它的边数为__。
2、已知一个多边形的每一个内角都是156°,则它的边数为__。815∵AB∥DE, CD∥AF(已知)∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等) ∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F∴∠FAB+∠C+∠E= 1/2 ×720°=360° 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:多边形的外角和等于360o3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和从上表中得到了什么结论?结论:任何多边形的外角和为360°(1)八边形的内角和为______,外角和为_____1080°360o(2)已知一个多边形的每一个外角都是72o,求这个边形的边数为______5∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°解:∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,∴∠CDE=∠FAB同理∠AFE=∠BCD,∠ABC=∠DEF∴∠FAB+∠BCD+∠DEF= ×720°=360°例: 一个六边形如图,已知AB∥DE,BC∥EF, CD∥AF,求∠A+∠C+∠E的度数。 拓展:一个六边形如图,已知 BA∥DE ,∠B= ∠ E,∠C=∠F
(1)求证:CD∥AF
(2)求∠A+∠C+∠E的度数.这节课你学到了什么?
还有什么困惑?1.“三个一”(一个定义、一个公式和一个性质)2. 一种重要数学思想方法(转化思想)谈一谈小结:是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)结论n边形的内角和为(n-2) ×180°(n≥3)n边形从一个顶点出发的对角线有(n-3)条(n≥3)任何多边形的外角和为360°
下定义 多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。 如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。 注意:n所代表的数字必须是汉字中的数字,如三角形,六边形,十边形等等,但当问题问这个多边形有多少条边时,我们可以用阿拉伯数字说明这个n边形有3条边,4条边等。根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角边顶点内角外角对角线组成多边形的线段叫做多边形的边相邻两边的交点叫做多边形的顶点相邻两边的夹角叫做多边形的内角多边形的边与它相邻的延长组成的角叫做多边形的外角连接多边形不相邻的两个顶点的线段叫做多边形的对角线想一想三角形有对角线吗?为什么?没有,因为三角形只有三个顶点,而这三个顶点是两两相邻的,它没有不相邻的顶点,所以三角形没有对角线。回想三角形的表示方法,这个多边形应该如何表示?首先给每个顶点标上一个大写字母,然后写出这个图形是几边形,最后再以一个字母为起点,沿顺时针或逆时针方向将字母按顺序写出。如四边形ABCD,五边形ABCDE,
n边形A1 A2A3A4A5A6···An A3 A4 A1 An A6 A5如图所示,观察两个图形,找出相同点和不同点如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形如果整个多边形不在这条直线的同一侧,那么这个多边形就是凹多边形另外,根据多边形的内角和是否大于180°,我们也可以区分这两种多边形。而中学阶段我们一般说的多边形都是凸多边形。观察下列图形,它们的边、角有什么特点?它们的边都相等,角也都相等各个角都相等,各条边都相等的多边形叫做正多边形。反过来,由定义可以得,正多边形有什么性质呢?练一练1、填空题
(1)连接多边形( )的线段,叫做多边形的多角形。
(2)多边形的任何( )所在的直线,整个多边形都在这条直线的( ),这样的多边形叫做凸多边形 。
(3)各个角( ),各条边( )的多边形,叫做正多边形。
(4)一个n边形有( )条边, ( )个顶点, ( )个内角, ( )个外角。
2、画出下列多边形的全部对角线不相邻的两个顶点一条边同一侧都相等都相等nnnn三角形的内角和是180°,那么四边形的内角和是多少呢?五边形呢?你是如何得到这个结论的?合作学习 B ACDE探究5边形内角和=3×180°=540°请你利用分割的方法探索五边形的内角是多少?E
ABCDO方法2180°× 5 – 360°= 540°180°× 5=900°?五边形内角和540°??把一个五边形分成几个三角形,还有其他的分法吗?ABCDEF180° × 4 – 180° = 540°方法3选择同一种方法分别求出任意六边形、七边形、八边形的内角和等于多少度?你能写出任意n边形的内角和吗?从五边形的一个顶点出发,可以引( )条对角线,他们将五边形分为多少个三角形,五边形的内角和等于180°×( )。从六边形的一个顶点出发,可以引( )条对角线,他们将六边形分为多少个三角形,六边形的内角和等于180°×( )。从七边形的一个顶点出发,可以引( )条对角线,他们将七边形分为多少个三角形,七边形的内角和等于180°×( )。我们是怎样求多边形内 角和的?就是从多边形的一个顶点出发,能引几条对角线把一个多边形分成几个三角形。总结:n边形内角和公式n边形内角和=(n-2) ·180°三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)合作学习请探索任意一个多边形的内角和与外角和的规律.………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°从上表中得到了什么结论?结论:n边形的内角和为:
(n-2)×180°(n≥3).n边形从一个顶点出发的对角线有(n-3)条(n≥3)练一练: (2)已知一个多边形的内角和为720o ,则这个多边形是______边形6 (3)在五边形ABCDE中,若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______80o(1)求十边形的内角和的度数。 解:(10-2)×180°=8 ×180°=1440°答:十边形的内角和是1440° 过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.3、填空(求边数)
1、已知一个多边形的内角和为1080°,则它的边数为__。
2、已知一个多边形的每一个内角都是156°,则它的边数为__。815∵AB∥DE, CD∥AF(已知)∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等) ∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F∴∠FAB+∠C+∠E= 1/2 ×720°=360° 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:多边形的外角和等于360o3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和从上表中得到了什么结论?结论:任何多边形的外角和为360°(1)八边形的内角和为______,外角和为_____1080°360o(2)已知一个多边形的每一个外角都是72o,求这个边形的边数为______5∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°解:∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,∴∠CDE=∠FAB同理∠AFE=∠BCD,∠ABC=∠DEF∴∠FAB+∠BCD+∠DEF= ×720°=360°例: 一个六边形如图,已知AB∥DE,BC∥EF, CD∥AF,求∠A+∠C+∠E的度数。 拓展:一个六边形如图,已知 BA∥DE ,∠B= ∠ E,∠C=∠F
(1)求证:CD∥AF
(2)求∠A+∠C+∠E的度数.这节课你学到了什么?
还有什么困惑?1.“三个一”(一个定义、一个公式和一个性质)2. 一种重要数学思想方法(转化思想)谈一谈小结:是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)结论n边形的内角和为(n-2) ×180°(n≥3)n边形从一个顶点出发的对角线有(n-3)条(n≥3)任何多边形的外角和为360°
