苏科版八年级上册第6章一次函数单元试题(Ⅰ卷)含答案
文档属性
| 名称 | 苏科版八年级上册第6章一次函数单元试题(Ⅰ卷)含答案 | 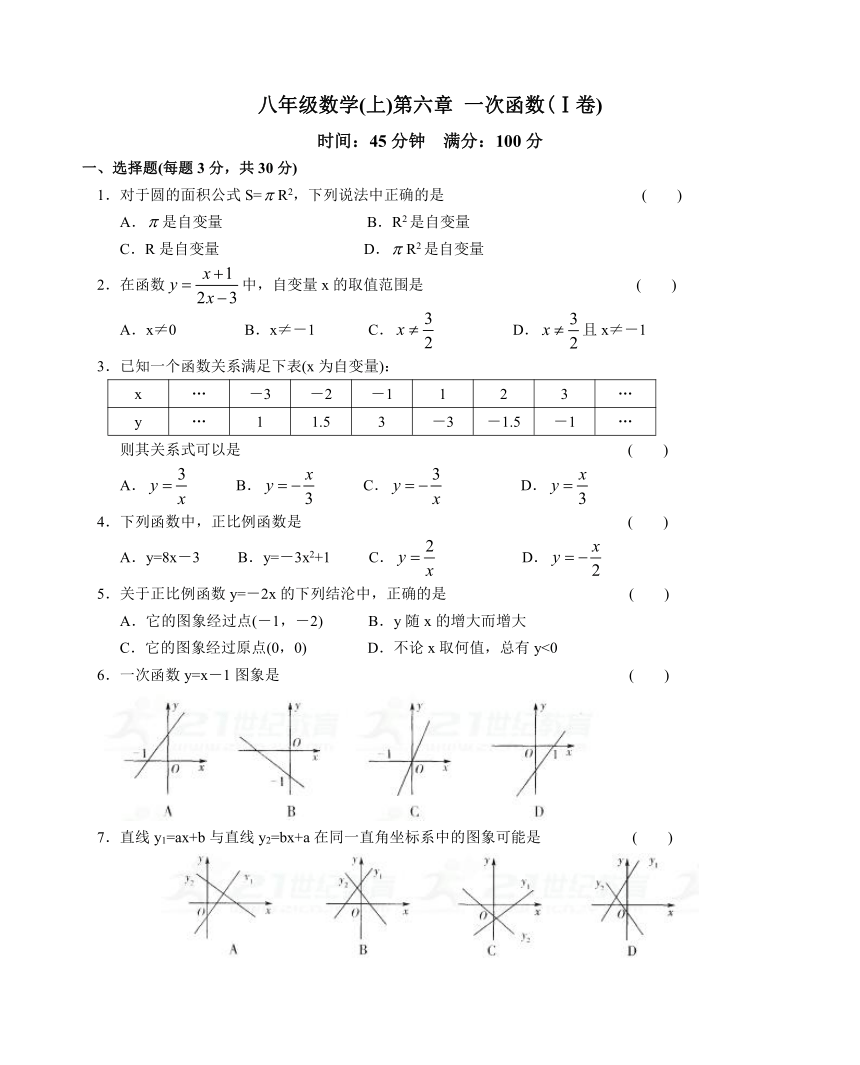 | |
| 格式 | zip | ||
| 文件大小 | 230.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-07 22:44:24 | ||
图片预览


文档简介
八年级数学(上)第六章
一次函数(Ⅰ卷)
时间:45分钟
满分:100分
一、选择题(每题3分,共30分)
1.对于圆的面积公式S=R2,下列说法中正确的是
(
)
A.是自变量
B.R2是自变量
C.R是自变量
D.R2是自变量
2.在函数中,自变量x的取值范围是
(
)
A.x≠0
B.x≠-1
C.
D.且x≠-1
3.已知一个函数关系满足下表(x为自变量):
x
…
-3
-2
-1
1
2
3
…
y
…
1
1.5
3
-3
-1.5
-1
…
则其关系式可以是
(
)
A.
B.
C.
D.
4.下列函数中,正比例函数是
(
)
A.y=8x-3
B.y=-3x2+1
C.
D.
5.关于正比例函数y=-2x的下列结沦中,正确的是
(
)
A.它的图象经过点(-1,-2)
B.y随x的增大而增大
C.它的图象经过原点(0,0)
D.不论x取何值,总有y<0
6.一次函数y=x-1图象是
(
)
7.直线y1=ax+b与直线y2=bx+a在同一直角坐标系中的图象可能是
(
)
8.已知一次函数y=kx+b,若k+b=1,则它的图象必过点
(
)
A.(-1,-1)
B.(1,1)
C.(-1,1)
D.(1,-1)
9.点P1
(x1,y1)和点P2(x2,y2)在同一直线y=-4x+3的图象上,且x1的关系是
(
)
A.y1>y2
B.y1C.y1=y2
D.y1>y2>0
10.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图
所示.若返回时上坡、下坡的速度仍保持不变,那么小明
从学校骑车回家用的时间是
(
)
A.48
min
B.33
min
C.30
min
D.37.2
min
三、填空题(每题3分,共30分)
11.已知y与x成正比例,并且当x=-3时,y=6,
则y与x的函数关系式为___________.
12.人们发现某种蟋蟀每分钟叫的次数n与温度T之间有这样一种近似关系:.若蟋蟀1
min叫的次数是60,则当时的温度约是_____℃.(精确到1℃)
13.一只蜡烛长28
cm,点燃后,每小时燃烧5
cm,剩余高度(cm)与燃烧时间t(h)的函数关系式为__________.
14.有一个密码系统,其原理由下面的框图所示:
当输出结果为10时,输入的x=________.
15.如果点P(-2,b)在直线y=2x-1上,那么点P到x轴的距离为__________.
16.直线y=6-2x与两坐标轴所围成的三角形的面积为_________.
17.如图,弹簧总长y(cm)与所挂物体质量x(kg)之间是一次函数关系,则弹簧不挂物体
时的长度为_________cm.
18.已知一次函数y=kx+b,当x=1时,y=-1;当x=2时,y=1,则当x=-1时,y=_______.
19.长途汽年客运公司规定旅客可随身携带一定重量的行李,若超过规定重量,则需购买行李票.行李费用y(元)与行李重量x(kg)之间的函数关系如图所示,则y与x之间的函数关系式是_________________,自变量x的取值范围是__________.
20.“龟兔赛跑”是同学们熟悉的寓言故事,如图表示路程
s(m)与时间t(min)之间的函数关系,则赛跑中兔子共
睡了__________min,乌龟在这次赛跑中的平均速度为
_________m/min.
三、解答题(每题10分,共40分)
21.某市出租车的计费标准如下:行驶路程不超过5
km
时,收费8元,行驶路程超过5
km的部分,按每千米1.5元计费.
(1)求出租车收费y(元)与行驶路程x(km)之间的函数关系式;
(2)若某人一次乘出租车付出了车费11元,求他这次乘坐了多少千米的路程
22.已知直线y1=-2x+4与直线,求两直线分别与x轴、y轴所围成的三角
形的面积.
23.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20
m3时,按2元/m3计费;月用水量超过20
m3时,其中的20
m3仍按2元/m3收费,超过部分按2.6元/m3计费.设每户家庭用用水量为x
m3时,应交水费y元.
(1)分别求出当0≤x≤20和x>20时,y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份
四月份
五月份
六月份
交费金额
小明家这个季度共用水多少立方米
24.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地走去,如图所示,图中的线段y1,y
2分别表示小东、小明离B地的距离(千米)与所用时间(小明)的关系.
(1)试用文字说明:交点P所表示的实际意义;
(2)试求出A、B两地之间的距离.
参考答案
1.C
2.C
3.C
4.D
5.C
6.D
7.A
8.B
9.A
10.D
11.y=-2x
12.32
13.=28-5t
14.4
15.5
16.9
17.15
18.-5
19.
30≤x≤130
20.30
10
21.(1)
(2)7
km
22.如图,两直线交点A的坐标为(3,-2),
∴
两直线与x轴所围三角形的面积.
两直线与y轴所围三角形的面积.
23.(1)当0≤x≤20时,y与x的函数表达式是y=2x;当x>20时,y与x的函数表达式是y=2×20+2.6(x-20),即y=2.6x-12;
(2)因为小明家四、五月份的消费都不超过40元,六月份的水费超过40元,所以把y=30代入y=2x中,得x=15;把y=4代入y=2x中,得x=17:把y=42.6代入y=2.6x-12中,得x=21.所以15+17+21=53.答:小明家这个季度共用水53立方米.
24.(1)交点P所表示的实际意义是:
经过2.5小时后,小东与小明在距离B地7.5千米处相遇.
(2)设y1=kx+b,又y1经过点P(2.5,7.5),(4,0)
∴解得
∴
y1=-5x+20,当x=0时,y1=20.故AB两地之间的距离为20千米.
一次函数(Ⅰ卷)
时间:45分钟
满分:100分
一、选择题(每题3分,共30分)
1.对于圆的面积公式S=R2,下列说法中正确的是
(
)
A.是自变量
B.R2是自变量
C.R是自变量
D.R2是自变量
2.在函数中,自变量x的取值范围是
(
)
A.x≠0
B.x≠-1
C.
D.且x≠-1
3.已知一个函数关系满足下表(x为自变量):
x
…
-3
-2
-1
1
2
3
…
y
…
1
1.5
3
-3
-1.5
-1
…
则其关系式可以是
(
)
A.
B.
C.
D.
4.下列函数中,正比例函数是
(
)
A.y=8x-3
B.y=-3x2+1
C.
D.
5.关于正比例函数y=-2x的下列结沦中,正确的是
(
)
A.它的图象经过点(-1,-2)
B.y随x的增大而增大
C.它的图象经过原点(0,0)
D.不论x取何值,总有y<0
6.一次函数y=x-1图象是
(
)
7.直线y1=ax+b与直线y2=bx+a在同一直角坐标系中的图象可能是
(
)
8.已知一次函数y=kx+b,若k+b=1,则它的图象必过点
(
)
A.(-1,-1)
B.(1,1)
C.(-1,1)
D.(1,-1)
9.点P1
(x1,y1)和点P2(x2,y2)在同一直线y=-4x+3的图象上,且x1
(
)
A.y1>y2
B.y1
D.y1>y2>0
10.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图
所示.若返回时上坡、下坡的速度仍保持不变,那么小明
从学校骑车回家用的时间是
(
)
A.48
min
B.33
min
C.30
min
D.37.2
min
三、填空题(每题3分,共30分)
11.已知y与x成正比例,并且当x=-3时,y=6,
则y与x的函数关系式为___________.
12.人们发现某种蟋蟀每分钟叫的次数n与温度T之间有这样一种近似关系:.若蟋蟀1
min叫的次数是60,则当时的温度约是_____℃.(精确到1℃)
13.一只蜡烛长28
cm,点燃后,每小时燃烧5
cm,剩余高度(cm)与燃烧时间t(h)的函数关系式为__________.
14.有一个密码系统,其原理由下面的框图所示:
当输出结果为10时,输入的x=________.
15.如果点P(-2,b)在直线y=2x-1上,那么点P到x轴的距离为__________.
16.直线y=6-2x与两坐标轴所围成的三角形的面积为_________.
17.如图,弹簧总长y(cm)与所挂物体质量x(kg)之间是一次函数关系,则弹簧不挂物体
时的长度为_________cm.
18.已知一次函数y=kx+b,当x=1时,y=-1;当x=2时,y=1,则当x=-1时,y=_______.
19.长途汽年客运公司规定旅客可随身携带一定重量的行李,若超过规定重量,则需购买行李票.行李费用y(元)与行李重量x(kg)之间的函数关系如图所示,则y与x之间的函数关系式是_________________,自变量x的取值范围是__________.
20.“龟兔赛跑”是同学们熟悉的寓言故事,如图表示路程
s(m)与时间t(min)之间的函数关系,则赛跑中兔子共
睡了__________min,乌龟在这次赛跑中的平均速度为
_________m/min.
三、解答题(每题10分,共40分)
21.某市出租车的计费标准如下:行驶路程不超过5
km
时,收费8元,行驶路程超过5
km的部分,按每千米1.5元计费.
(1)求出租车收费y(元)与行驶路程x(km)之间的函数关系式;
(2)若某人一次乘出租车付出了车费11元,求他这次乘坐了多少千米的路程
22.已知直线y1=-2x+4与直线,求两直线分别与x轴、y轴所围成的三角
形的面积.
23.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20
m3时,按2元/m3计费;月用水量超过20
m3时,其中的20
m3仍按2元/m3收费,超过部分按2.6元/m3计费.设每户家庭用用水量为x
m3时,应交水费y元.
(1)分别求出当0≤x≤20和x>20时,y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份
四月份
五月份
六月份
交费金额
小明家这个季度共用水多少立方米
24.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地走去,如图所示,图中的线段y1,y
2分别表示小东、小明离B地的距离(千米)与所用时间(小明)的关系.
(1)试用文字说明:交点P所表示的实际意义;
(2)试求出A、B两地之间的距离.
参考答案
1.C
2.C
3.C
4.D
5.C
6.D
7.A
8.B
9.A
10.D
11.y=-2x
12.32
13.=28-5t
14.4
15.5
16.9
17.15
18.-5
19.
30≤x≤130
20.30
10
21.(1)
(2)7
km
22.如图,两直线交点A的坐标为(3,-2),
∴
两直线与x轴所围三角形的面积.
两直线与y轴所围三角形的面积.
23.(1)当0≤x≤20时,y与x的函数表达式是y=2x;当x>20时,y与x的函数表达式是y=2×20+2.6(x-20),即y=2.6x-12;
(2)因为小明家四、五月份的消费都不超过40元,六月份的水费超过40元,所以把y=30代入y=2x中,得x=15;把y=4代入y=2x中,得x=17:把y=42.6代入y=2.6x-12中,得x=21.所以15+17+21=53.答:小明家这个季度共用水53立方米.
24.(1)交点P所表示的实际意义是:
经过2.5小时后,小东与小明在距离B地7.5千米处相遇.
(2)设y1=kx+b,又y1经过点P(2.5,7.5),(4,0)
∴解得
∴
y1=-5x+20,当x=0时,y1=20.故AB两地之间的距离为20千米.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
