2017年秋人教版七年级上《4.3.2角的比较与运算》同步四维训练含答案
文档属性
| 名称 | 2017年秋人教版七年级上《4.3.2角的比较与运算》同步四维训练含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 344.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-07 00:00:00 | ||
图片预览

文档简介
4.3.2 角的比较与运算
知识点一:角的比较与角的和差
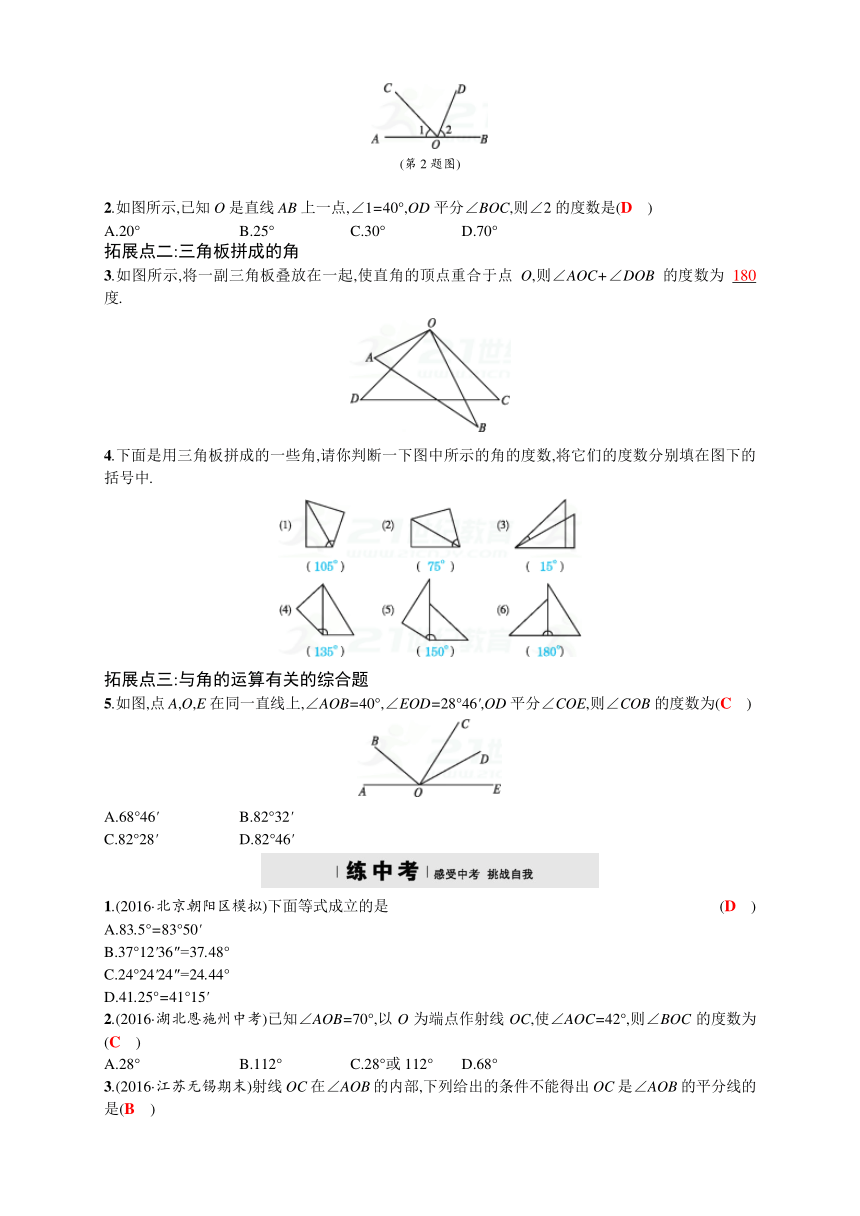
1.如图,∠AOD-∠AOC=∠COD .
知识点二:角的平分线
2.
如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式正确的是(D )
A.∠COD=∠AOB
B.∠AOD=∠AOB
C.∠BOD=∠AOD
D.∠BOC=∠AOD
3.如图,在△ABC中,AB=AC,BD为∠ABC的平分线,∠BDC=84°,则∠A=52° .
知识点三:角的运算
4.计算180°-48°39'40″-67°41'35″的值是(A )
A.63°38'45″
B.58°39'40″
C.64°39'40″
D.63°78'65″
拓展点一:角平分线及角的和、差计算
1.如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠BOC=50°,则∠COD=(B )
A.50°
B.25°
C.100°
D.75°
(第1题图)
(第2题图)
2.如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是(D )
A.20°
B.25°
C.30°
D.70°
拓展点二:三角板拼成的角
3.如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为180 度.
4.下面是用三角板拼成的一些角,请你判断一下图中所示的角的度数,将它们的度数分别填在图下的括号中.
拓展点三:与角的运算有关的综合题
5.如图,点A,O,E在同一直线上,∠AOB=40°,∠EOD=28°46',OD平分∠COE,则∠COB的度数为(C )
A.68°46'
B.82°32'
C.82°28'
D.82°46'
1.(2016·北京朝阳区模拟)下面等式成立的是
(D )
A.83.5°=83°50'
B.37°12'36″=37.48°
C.24°24'24″=24.44°
D.41.25°=41°15'
2.(2016·湖北恩施州中考)已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为(C )
A.28°
B.112°
C.28°或112°
D.68°
3.(2016·江苏无锡期末)射线OC在∠AOB的内部,下列给出的条件不能得出OC是∠AOB的平分线的是(B )
A.∠AOC=∠BOC
B.∠AOC+∠BOC=∠AOB
C.∠AOB=2∠AOC
D.∠BOC=∠AOB
4.
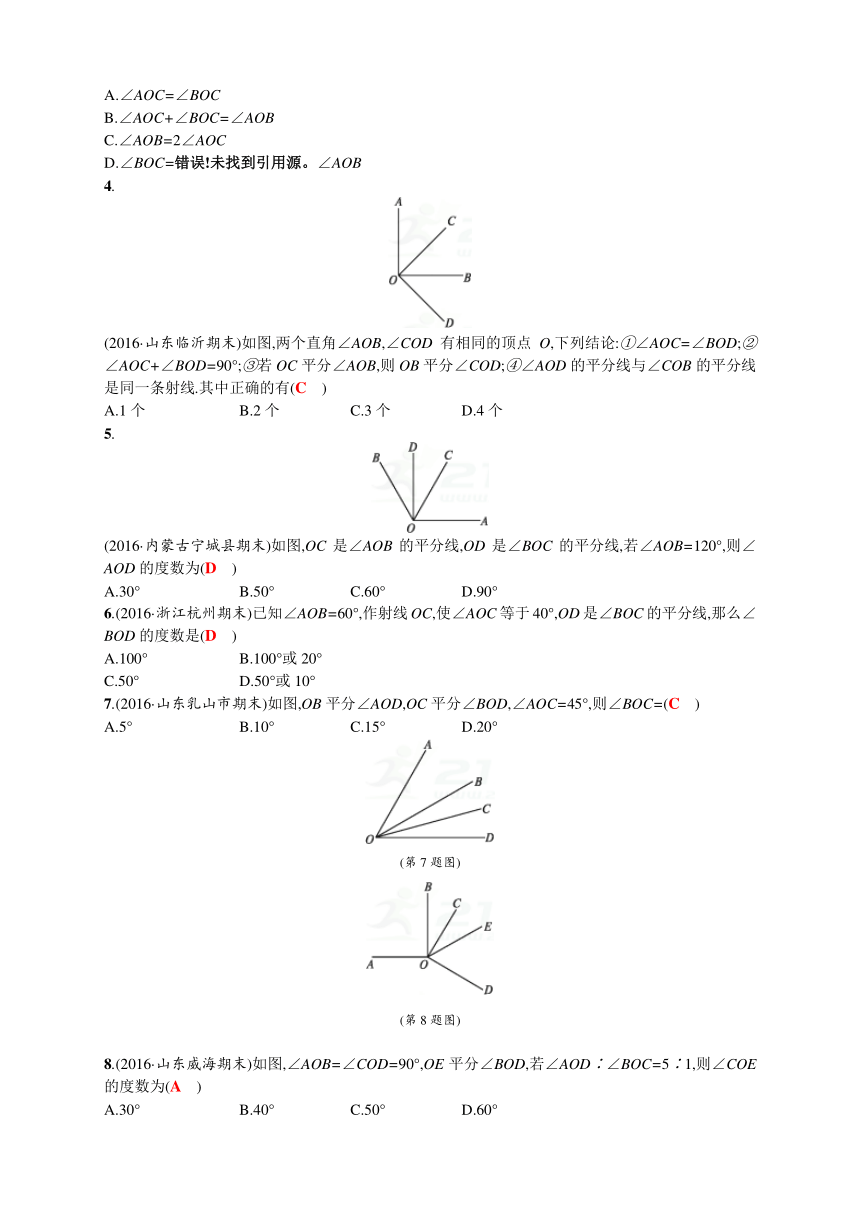
(2016·山东临沂期末)如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线.其中正确的有(C )
A.1个
B.2个
C.3个
D.4个
5.
(2016·内蒙古宁城县期末)如图,OC是∠AOB的平分线,OD是∠BOC的平分线,若∠AOB=120°,则∠AOD的度数为(D )
A.30°
B.50°
C.60°
D.90°
6.(2016·浙江杭州期末)已知∠AOB=60°,作射线OC,使∠AOC等于40°,OD是∠BOC的平分线,那么∠BOD的度数是(D )
A.100°
B.100°或20°
C.50°
D.50°或10°
7.(2016·山东乳山市期末)如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=(C )
A.5°
B.10°
C.15°
D.20°
(第7题图)
(第8题图)
8.(2016·山东威海期末)如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD∶∠BOC=5∶1,则∠COE的度数为(A )
A.30°
B.40°
C.50°
D.60°
9.(2016·福建仙游县期末)把两块三角板按如图所示那样拼在一起,则∠ABC等于(D )
A.70°
B.90°
C.105°
D.120°
10.(2015·山东招远市期末)计算:
(1)40°26'+30°30'30″÷6;
(2)13°53'×3-32°5'31″.
解(1)40°26'+30°30'30″÷6=40°26'+5°5'5″=45°31'5″;
(2)13°53'×3-32°5'31″=41°39'-32°5'31″=9°33'29″.
11.
(2015·甘肃张掖月考)把一副三角尺按如图所示拼在一起.
(1)写出图中∠A,∠B,∠BCD,∠D,∠AED的度数;
(2)用小于号“<”将上述各角连接起来.
解(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°;
(2)∠A<∠D<∠B<∠AED<∠BCD.
12.(2016·贵州望谟县期末)如图,已知∠AOD∶∠BOD=1∶3,OC是∠AOD的平分线.若∠AOB=120°,求:
(1)∠COD的度数.
(2)∠BOC的度数.
解(1)∵∠AOD∶∠BOD=1∶3,
∴设∠AOD=x°,则∠BOD=3x°,
又∵∠AOB=120°,
∴∠AOD+∠BOD=∠AOB=120°,
∴x+3x=120,解得x=30,
∵OC是∠AOD的平分线,
∴∠COD=∠AOC=∠AOD
=×30°=15°;
(2)由(1)得∠BOC=∠AOB-∠AOC=120°-15°=105°.
13.(2016·辽宁新宾县期末)已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C,E,F在直线AB的同侧(如图1所示)时,
①若∠COF=25°,则∠BOE= .
②猜想∠COF与∠BOE的数量关系是 .
(2)当点C与点E,F在直线AB的两旁(如图2所示)时,(1)题②中的结论是否仍然成立 请说明理由.
图1
图2
解(1)(1)①50°
②∠BOE=2∠COF;
(2)(1)题②中的结论仍然成立.理由如下:
∵OF是∠AOE的平分线,
∴∠EOF=∠AOE,
∵∠COE=90°,∴∠EOF=90°-∠COF,
又∠AOE+∠BOE=180°,
∴90°-∠COF=(180°-∠BOE),
∴∠BOE=2∠COF.
知识点一:角的比较与角的和差
1.如图,∠AOD-∠AOC=∠COD .
知识点二:角的平分线
2.
如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式正确的是(D )
A.∠COD=∠AOB
B.∠AOD=∠AOB
C.∠BOD=∠AOD
D.∠BOC=∠AOD
3.如图,在△ABC中,AB=AC,BD为∠ABC的平分线,∠BDC=84°,则∠A=52° .
知识点三:角的运算
4.计算180°-48°39'40″-67°41'35″的值是(A )
A.63°38'45″
B.58°39'40″
C.64°39'40″
D.63°78'65″
拓展点一:角平分线及角的和、差计算
1.如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠BOC=50°,则∠COD=(B )
A.50°
B.25°
C.100°
D.75°
(第1题图)
(第2题图)
2.如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是(D )
A.20°
B.25°
C.30°
D.70°
拓展点二:三角板拼成的角
3.如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为180 度.
4.下面是用三角板拼成的一些角,请你判断一下图中所示的角的度数,将它们的度数分别填在图下的括号中.
拓展点三:与角的运算有关的综合题
5.如图,点A,O,E在同一直线上,∠AOB=40°,∠EOD=28°46',OD平分∠COE,则∠COB的度数为(C )
A.68°46'
B.82°32'
C.82°28'
D.82°46'
1.(2016·北京朝阳区模拟)下面等式成立的是
(D )
A.83.5°=83°50'
B.37°12'36″=37.48°
C.24°24'24″=24.44°
D.41.25°=41°15'
2.(2016·湖北恩施州中考)已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为(C )
A.28°
B.112°
C.28°或112°
D.68°
3.(2016·江苏无锡期末)射线OC在∠AOB的内部,下列给出的条件不能得出OC是∠AOB的平分线的是(B )
A.∠AOC=∠BOC
B.∠AOC+∠BOC=∠AOB
C.∠AOB=2∠AOC
D.∠BOC=∠AOB
4.
(2016·山东临沂期末)如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线.其中正确的有(C )
A.1个
B.2个
C.3个
D.4个
5.
(2016·内蒙古宁城县期末)如图,OC是∠AOB的平分线,OD是∠BOC的平分线,若∠AOB=120°,则∠AOD的度数为(D )
A.30°
B.50°
C.60°
D.90°
6.(2016·浙江杭州期末)已知∠AOB=60°,作射线OC,使∠AOC等于40°,OD是∠BOC的平分线,那么∠BOD的度数是(D )
A.100°
B.100°或20°
C.50°
D.50°或10°
7.(2016·山东乳山市期末)如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=(C )
A.5°
B.10°
C.15°
D.20°
(第7题图)
(第8题图)
8.(2016·山东威海期末)如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD∶∠BOC=5∶1,则∠COE的度数为(A )
A.30°
B.40°
C.50°
D.60°
9.(2016·福建仙游县期末)把两块三角板按如图所示那样拼在一起,则∠ABC等于(D )
A.70°
B.90°
C.105°
D.120°
10.(2015·山东招远市期末)计算:
(1)40°26'+30°30'30″÷6;
(2)13°53'×3-32°5'31″.
解(1)40°26'+30°30'30″÷6=40°26'+5°5'5″=45°31'5″;
(2)13°53'×3-32°5'31″=41°39'-32°5'31″=9°33'29″.
11.
(2015·甘肃张掖月考)把一副三角尺按如图所示拼在一起.
(1)写出图中∠A,∠B,∠BCD,∠D,∠AED的度数;
(2)用小于号“<”将上述各角连接起来.
解(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°;
(2)∠A<∠D<∠B<∠AED<∠BCD.
12.(2016·贵州望谟县期末)如图,已知∠AOD∶∠BOD=1∶3,OC是∠AOD的平分线.若∠AOB=120°,求:
(1)∠COD的度数.
(2)∠BOC的度数.
解(1)∵∠AOD∶∠BOD=1∶3,
∴设∠AOD=x°,则∠BOD=3x°,
又∵∠AOB=120°,
∴∠AOD+∠BOD=∠AOB=120°,
∴x+3x=120,解得x=30,
∵OC是∠AOD的平分线,
∴∠COD=∠AOC=∠AOD
=×30°=15°;
(2)由(1)得∠BOC=∠AOB-∠AOC=120°-15°=105°.
13.(2016·辽宁新宾县期末)已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C,E,F在直线AB的同侧(如图1所示)时,
①若∠COF=25°,则∠BOE= .
②猜想∠COF与∠BOE的数量关系是 .
(2)当点C与点E,F在直线AB的两旁(如图2所示)时,(1)题②中的结论是否仍然成立 请说明理由.
图1
图2
解(1)(1)①50°
②∠BOE=2∠COF;
(2)(1)题②中的结论仍然成立.理由如下:
∵OF是∠AOE的平分线,
∴∠EOF=∠AOE,
∵∠COE=90°,∴∠EOF=90°-∠COF,
又∠AOE+∠BOE=180°,
∴90°-∠COF=(180°-∠BOE),
∴∠BOE=2∠COF.
