2017年秋人教版七年级上《4.4课题学习--设计制作长方体形状的包装纸盒》同步四维训练含答案
文档属性
| 名称 | 2017年秋人教版七年级上《4.4课题学习--设计制作长方体形状的包装纸盒》同步四维训练含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 306.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-07 23:49:09 | ||
图片预览

文档简介
4.3.3 余角和补角
4.4 课题学习 设计制作长方体形状的包装纸盒
知识点一:余角和补角的概念
1.如图所示,∠1是锐角,则∠1的余角是(C )
A.∠2-∠1
B.∠2-∠1
C.(∠2-∠1)
D.(∠2+∠1)
知识点二:余角和补角的性质
2.
如图,△ABC中,∠ACB=90°,∠CDB=90°,则图中所有与∠B互余的角为∠A,∠2 .
3.
如图,已知AB是一条直线,∠1=∠2,∠3=∠4,∠AOF=90°.
(1)∠AOC的补角是∠BOC ;
(2)∠3,∠4 是∠AOC的余角;
(3)∠DOC的余角是∠DOF ;
(4)∠COF的补角是∠AOE .
拓展点一:方向角
1.
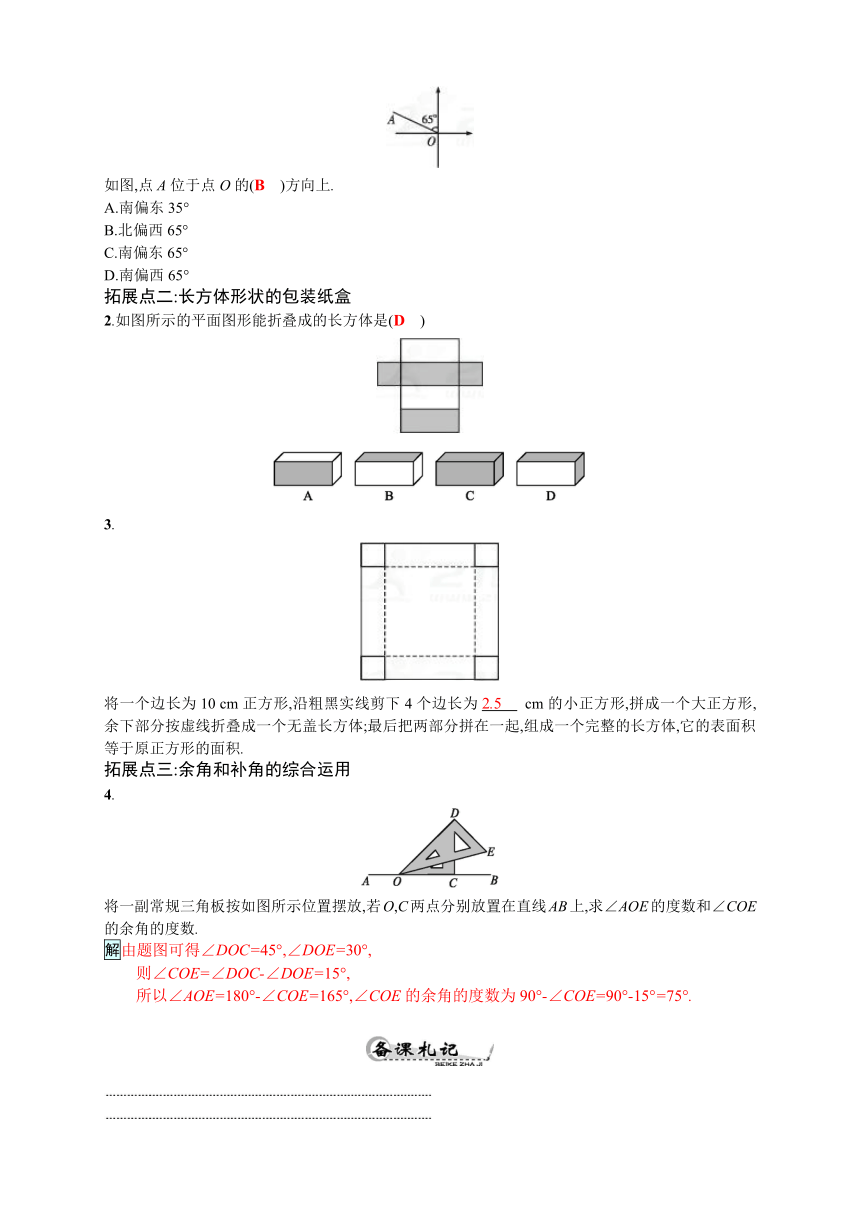
如图,点A位于点O的(B )方向上.
A.南偏东35°
B.北偏西65°
C.南偏东65°
D.南偏西65°
拓展点二:长方体形状的包装纸盒
2.如图所示的平面图形能折叠成的长方体是(D )
3.
将一个边长为10
cm正方形,沿粗黑实线剪下4个边长为2.5
cm的小正方形,拼成一个大正方形,余下部分按虚线折叠成一个无盖长方体;最后把两部分拼在一起,组成一个完整的长方体,它的表面积等于原正方形的面积.
拓展点三:余角和补角的综合运用
4.
将一副常规三角板按如图所示位置摆放,若O,C两点分别放置在直线AB上,求∠AOE的度数和∠COE的余角的度数.
解由题图可得∠DOC=45°,∠DOE=30°,
则∠COE=∠DOC-∠DOE=15°,
所以∠AOE=180°-∠COE=165°,∠COE的余角的度数为90°-∠COE=90°-15°=75°.
1.(2016·河北模拟)下列图形中,∠1与∠2互为补角的是(C )
2.(2017·上海宝山区一模)如果从甲船看乙船,乙船在甲船的北偏东30°方向,那么从乙船看甲船,甲船在乙船的(A )
A.南偏西30°方向
B.南偏西60°方向
C.南偏东30°方向
D.南偏东60°方向
3(2015·上海黄埔区一模)图中各硬纸片,不可以沿虚线折叠成长方体纸盒的是(C )
A.①②
B.②③
C.③④
D.①④
4.(2016·广东茂名中考)已知∠A=100°,那么∠A补角为80 度.
5.(2017·上海普陀区一模)如果港口A的南偏东52°方向有一座小岛B,那么从小岛B观察港口A的方向是北偏西52° .
6.
(2016·山东济宁期末)如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB=105 °.
7.
(2016·河南漯河期末)如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=180° .
8.某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料(单位:毫米).
(1)此长方体包装盒的体积为 立方毫米(用含x,y的式子表示).
(2)若内部粘贴角料的面积占长方体表面纸板面积的,则当x=40,y=70时,制作这样一个长方体共需要纸板多少平方毫米
解(1)65xy;
(2)因为长方体的长为y毫米,宽为65毫米,高为x毫米,
所以长方体的表面积=2(xy+65y+65x)平方毫米,又因为内部粘贴角料的面积占长方体表面纸板面积的,所以制作这样一个长方体共需要纸板的面积=×2(xy+65y+65x)=(xy+65y+65x)=xy+156y+156x(平方毫米),因为x=40,y=70,所以制作这样一个长方体共需要纸板×40×70+156×70+156×40=23
880(平方毫米).
9.
(2015·安徽黄山期末)在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的,如图,用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角,从A到B的飞行方向角为35°,从A到C的飞行方向角为60°,从A到D的飞行方向角为145°,试求AB与AC之间夹角为多少度 AD与AC之间夹角为多少度 并画出从A飞出且方向角为105°的飞行线.
解由题意可知∠NAB=35°,∠NAC=60°,∠NAD=145°.
故AB与AC之间夹角为∠NAC-∠NAB=60°-35°=25°,AD与AC之间夹角为∠NAD-∠NAC=145°-60°=85°,从A飞出且方向角为105°的飞行线如图中AE.
4.4 课题学习 设计制作长方体形状的包装纸盒
知识点一:余角和补角的概念
1.如图所示,∠1是锐角,则∠1的余角是(C )
A.∠2-∠1
B.∠2-∠1
C.(∠2-∠1)
D.(∠2+∠1)
知识点二:余角和补角的性质
2.
如图,△ABC中,∠ACB=90°,∠CDB=90°,则图中所有与∠B互余的角为∠A,∠2 .
3.
如图,已知AB是一条直线,∠1=∠2,∠3=∠4,∠AOF=90°.
(1)∠AOC的补角是∠BOC ;
(2)∠3,∠4 是∠AOC的余角;
(3)∠DOC的余角是∠DOF ;
(4)∠COF的补角是∠AOE .
拓展点一:方向角
1.
如图,点A位于点O的(B )方向上.
A.南偏东35°
B.北偏西65°
C.南偏东65°
D.南偏西65°
拓展点二:长方体形状的包装纸盒
2.如图所示的平面图形能折叠成的长方体是(D )
3.
将一个边长为10
cm正方形,沿粗黑实线剪下4个边长为2.5
cm的小正方形,拼成一个大正方形,余下部分按虚线折叠成一个无盖长方体;最后把两部分拼在一起,组成一个完整的长方体,它的表面积等于原正方形的面积.
拓展点三:余角和补角的综合运用
4.
将一副常规三角板按如图所示位置摆放,若O,C两点分别放置在直线AB上,求∠AOE的度数和∠COE的余角的度数.
解由题图可得∠DOC=45°,∠DOE=30°,
则∠COE=∠DOC-∠DOE=15°,
所以∠AOE=180°-∠COE=165°,∠COE的余角的度数为90°-∠COE=90°-15°=75°.
1.(2016·河北模拟)下列图形中,∠1与∠2互为补角的是(C )
2.(2017·上海宝山区一模)如果从甲船看乙船,乙船在甲船的北偏东30°方向,那么从乙船看甲船,甲船在乙船的(A )
A.南偏西30°方向
B.南偏西60°方向
C.南偏东30°方向
D.南偏东60°方向
3(2015·上海黄埔区一模)图中各硬纸片,不可以沿虚线折叠成长方体纸盒的是(C )
A.①②
B.②③
C.③④
D.①④
4.(2016·广东茂名中考)已知∠A=100°,那么∠A补角为80 度.
5.(2017·上海普陀区一模)如果港口A的南偏东52°方向有一座小岛B,那么从小岛B观察港口A的方向是北偏西52° .
6.
(2016·山东济宁期末)如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB=105 °.
7.
(2016·河南漯河期末)如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=180° .
8.某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料(单位:毫米).
(1)此长方体包装盒的体积为 立方毫米(用含x,y的式子表示).
(2)若内部粘贴角料的面积占长方体表面纸板面积的,则当x=40,y=70时,制作这样一个长方体共需要纸板多少平方毫米
解(1)65xy;
(2)因为长方体的长为y毫米,宽为65毫米,高为x毫米,
所以长方体的表面积=2(xy+65y+65x)平方毫米,又因为内部粘贴角料的面积占长方体表面纸板面积的,所以制作这样一个长方体共需要纸板的面积=×2(xy+65y+65x)=(xy+65y+65x)=xy+156y+156x(平方毫米),因为x=40,y=70,所以制作这样一个长方体共需要纸板×40×70+156×70+156×40=23
880(平方毫米).
9.
(2015·安徽黄山期末)在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的,如图,用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角,从A到B的飞行方向角为35°,从A到C的飞行方向角为60°,从A到D的飞行方向角为145°,试求AB与AC之间夹角为多少度 AD与AC之间夹角为多少度 并画出从A飞出且方向角为105°的飞行线.
解由题意可知∠NAB=35°,∠NAC=60°,∠NAD=145°.
故AB与AC之间夹角为∠NAC-∠NAB=60°-35°=25°,AD与AC之间夹角为∠NAD-∠NAC=145°-60°=85°,从A飞出且方向角为105°的飞行线如图中AE.
