第六章 一次函数单元检测卷含答案

第6章
一次函数
单元检测卷
(时间：60分钟
分值：100分)
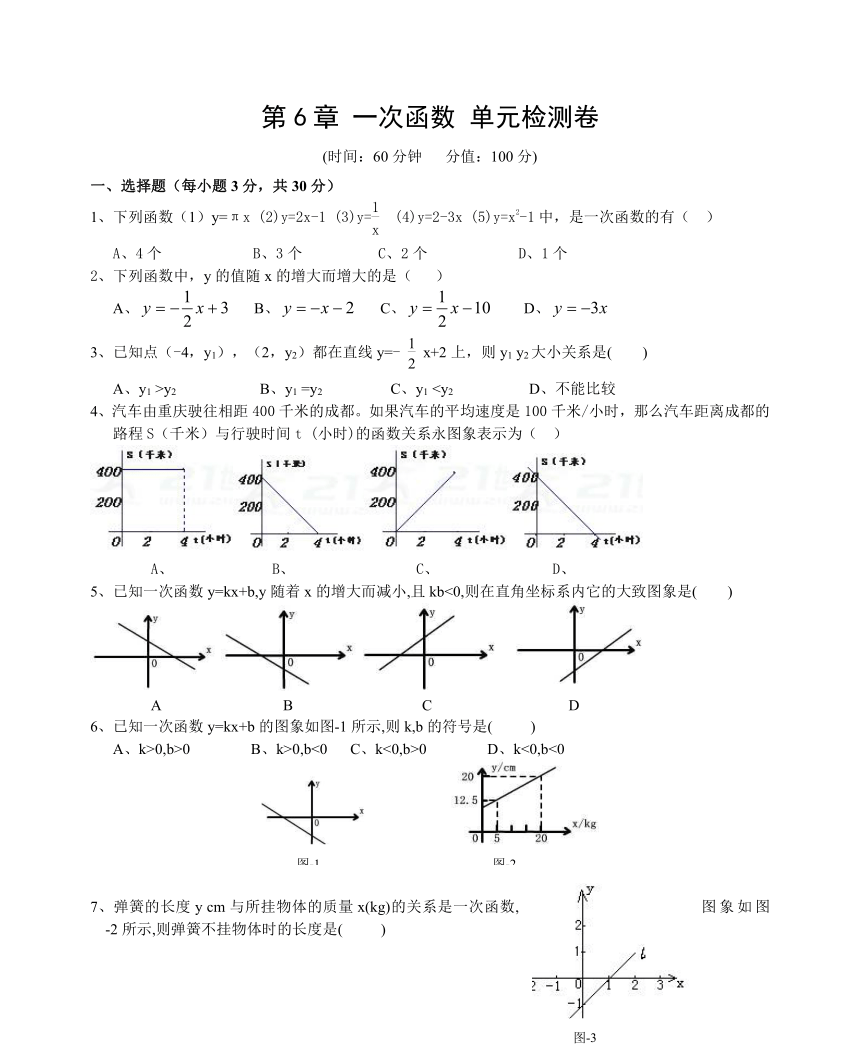
一、选择题（每小题3分，共30分）
1、下列函数（1）y=πx
(2)y=2x-1
(3)y=
(4)y=2-3x
(5)y=x2-1中，是一次函数的有（
）
A、4个
B、3个
C、2个
D、1个
2、下列函数中，y的值随x的增大而增大的是（
）
A、
B、
C、
D、
3、已知点（-4，y1），（2，y2）都在直线y=-
x+2上，则y1
y2大小关系是(
)
A、y1
>y2
B、y1
=y2
C、y1
D、不能比较
4、汽车由重庆驶往相距400千米的成都。如果汽车的平均速度是100千米/小时，那么汽车距离成都的路程S（千米）与行驶时间t
(小时)的函数关系永图象表示为（
）
A、
B、
C、
D、
5、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是(
)
A
B
C
D
6、已知一次函数y=kx+b的图象如图-1所示,则k,b的符号是(
)
A、k>0,b>0
B、k>0,b<0
C、k<0,b>0
D、k<0,b<0
7、弹簧的长度y
cm与所挂物体的质量x(kg)的关系是一次函数,图象如图-2所示,则弹簧不挂物体时的长度是(
)
A、9cm
B、10cm
C、10.5cm
D、11cm
8、如图-3，在直角坐标系中，直线l对应的函数数表达式是（
）
A、
B、
C、
D、
9、下列图象中，与关系式表示的是同一个一次函数的图象是（
）
10、已知函数与的图象交于点P，则点P的坐标是（
）
A、（－7，－3）
B、（3，－7）
C、（－3，－7）
D、（－3，7）
二、填空题（每小题3分，共21分）
11、某种储蓄的月利率为0.15‰，现存入1000元，则本息和y（元）与所存月数x之间的函数关系式是
.
12、若函数y=
-2xm+2是正比例函数，则m的值是
.
13、一次函数y=
-2x+4的图象与x轴交点坐标是
，与y轴交点坐标是
图象与坐标轴所围成的三角形面积是
.
14、写出同时具备下列两个条件的一次函数表达式（写出一个即可）
.
（1）y随着x的增大而减小。
（2）图象经过点（1，-3）
15、某商店出售一种瓜子，其售价y（元）与瓜子质量x（千克）之间的关系如下表
质量x（千克）
1
2
3
4
……
售价y（元）
3.60+0.20
7.20+0.20
10.80+0.20
14.40+0.2
……
由上表得y与x之间的关系式是
.
16、某人用充值50元的IC卡从A地向B地打长途电话，按通话时间收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若此人第一次通话t分钟（3≤t≤45），则IC卡上所余的费用y（元）与t（分）之间的关系式是
.
17、如图-4，已知A地在B地正南方3千米处，甲乙两人同时分别从A、B两地向正北方向匀速直行，他们与A地的距离S（千米）与所行的时间t（小时）之间的函数关系图象如图所示的AC和BD给出，当他们行走3小时后，他们之间的距离为
千米.
三、解答题(第18~21题,每题7分,第22题10分,
第23题11分,共49分)
18、已知y
-2与x成正比,且当x=1时,y=
-6
(1)求y与x之间的函数关系式;
(2)若点(a,2)在这个函数图象上,求a.
19、已知函数y=(2m+1)x+m
-3
(1)若函数图象经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
20、已知一次函数y=kx+b的图象经过点(-1,
-5),且与正比例函数y=
x的图象相交于点(2,a),求：
(1)a的值;(2)k,b的值;(3)这两个函数图象与x轴所围成的三角形面积.
21、如图-5是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题：
(1)当行使8千米时,收费应为
元
(2)从图象上你能获得哪些信息 (请写出2条)
①
②
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式
22、一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图-6所示,结合图象回答下列问题.
(1)农民自带的零钱是多少
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆
23、某移动通讯公司开设两种业务。“全球通”：先缴50元月租费，然后每通话1跳次，再付0.4元；“神州行”：不缴月租费，每通话1跳次，付话费0.6元（本题的通话均指市内通话）。若设一个月通话x跳次，两种方式的费用分别为元和元。（跳次：1分钟是1跳次，不足1分钟按1跳次算，如3.2分钟为4跳次）
（1）写出和与间的函数关系式；
（2）一个月通话多少跳次，两种费用相同？
（3）某人估计一个月内通话300跳次，应选择哪种合算？
参考答案
一、选择题
1、B
2、C
3、A
4、D
5、A
6、D
7、B
8、A
9、D
10、C
填空题（每题3分共30分）
11、y=15x+1000
12、－1
13、（2，0），（0，4），4
14、
15、y=3.60x+0.20
16、y=50.6－x
17、1.5
解答题
18、
（2）
19、（1）
（2）
20、（1）
（2）
（3）面积为
21、（1）11；（2）如：出租车起步价
（3千米内）为5元；超出3千米，每千米加收1.2元等
（3）
22、（1）5
（2）
（3）0.5元
（4）45千克
23、解：（1）。
（2）两种费用相同时，=，即。
解之得
（3）某人一个月估计通话300跳次，则：
全球通费用为（元），
神州行费用为（元）。
∵<，∴应选择“全球通”合算。
图-1
图-2
图-3
图-4
图-5
图-6