第六章 一次函数阶段测试卷含答案

初二数学阶段测试卷(一次函数)
(时间：60分钟
满分：l
00分)
一、选择题(每题2分．共22分)
1．一次函数y=2x+3的图象不经过(
)．
A．第一象限
B．第二象限
C．第三象限
D．第四象限
2．如果点A(3，a)、B(3,
4)关于x轴对称，那么a的值为
(
)．
A．3
B.
3
C．4
D．4
3．下面哪个点不在函数y=2x+3的图象上(
)．
A．(5，13)
B．(0.5,
2)
C．(3，0)
D．(1,
1)
4．台风是一种破坏性极大的自然灾害．气象台为预报台风，首先要确定它的位置，下列说法能确定台风位置的是(
)．
A．北纬260，东经1330
B．西太平洋
C．距离台湾300海里
D．台湾与冲绳岛之间
5．下列函数中,
y随x的增大而减小的有(
)．
①y=2x+1；②y=6x
③y=；④y=(1)x
A．1个
B．2个
C．3个
D．4个
6．两个一次函数y=x4和y=3x+3图象的交点坐标是(
)．
A．(2．3)
B．(2,
3)
C．(2,
3)
D．(2,
3)
7．汽车开始行驶时，油箱内有油40L．如果每小时耗油5L。则油箱内的余油量Q(L)与行驶时间t(h)之间的函数关系的图象应是(
)．
8．如图是某函数的图象，则下列结论中正确的是(
)．
A．当y=1时,
x的取值是,
5
B．当y=3时,
x的取值是0,
2
C．当x=时,
函数y值最大
D．当x>3时,
y随x的增大而增大
9．小明所在学校离家距离为2
km，某天他放学后骑自行车回家，行驶了5
min后。因故停留10
min．继续骑了5
min到家．下面哪一个图象能大致描述他回家过程中离家的距离s
(km)与所用时间t(mm)之间的关系(
)．
10．一次函数y=kx+b的图像如图，则其函数关系式为(
)．
A．y=x+2
B．y=x+2
C．y=x+2
D．y=x+2
11．若一次函数y=kx+b中,
k>0,
b<0．则它的图象的基本特征如图(
)．
二、填空题(每题4分，共24分)
12．点P(m+3，m+1)在直角坐标系的y轴上，则点P的坐标为______．
13．平行四边形ABCD的对角线的交点O为直角坐标系的坐标原点，点A(2，1)，点B(，1)，则点C和D的坐标分别为______．
14．已知一次函数y=kx+5的图象经过点(3，2)，则是k=____________．
15．在直线y=x+2上，到y轴距离为2个单位长度的点的坐标为______．
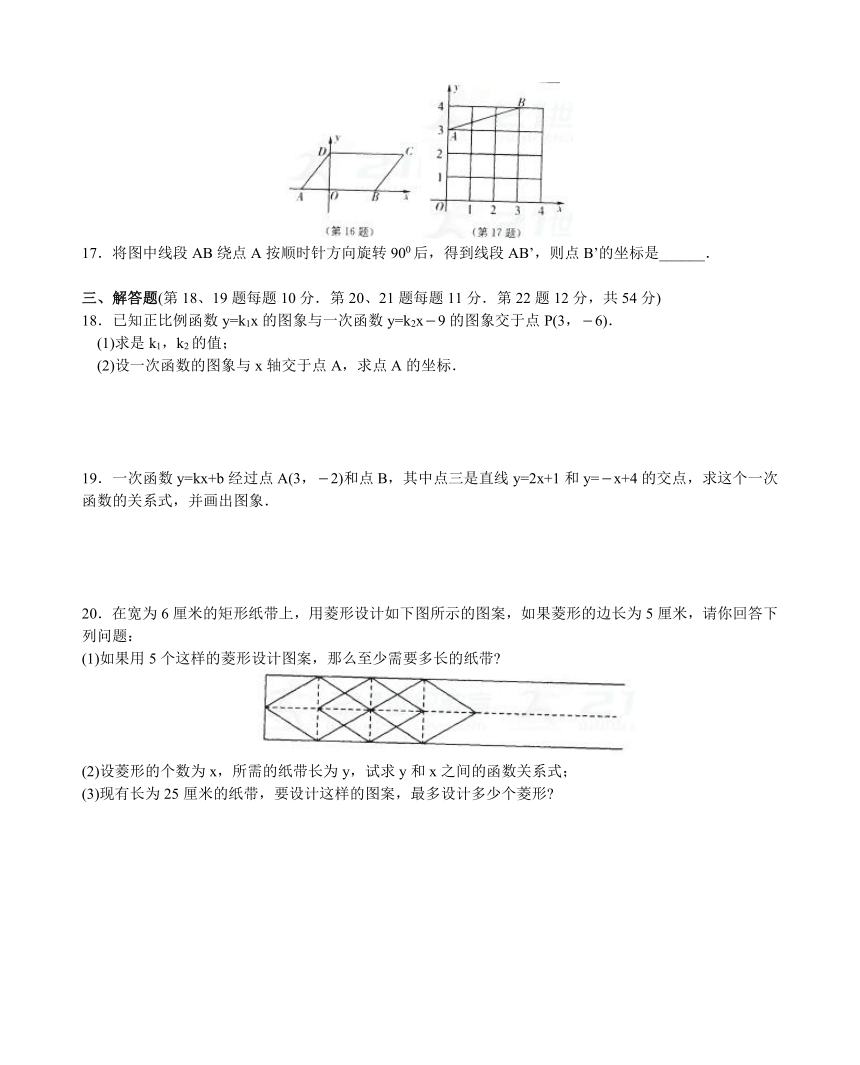
16．如图，在ABCD中，AD=5,
AB=8，点A的坐标为
(3，0)，则点C的坐标为______．
17．将图中线段AB绕点A按顺时针方向旋转900后，得到线段AB’，则点B’的坐标是______．
三、解答题(第18、19题每题10分．第20、21题每题11分．第22题12分，共54分)
18．已知正比例函数y=k1x的图象与一次函数y=k2x9的图象交于点P(3，6)．
(1)求是k1，k2的值；
(2)设一次函数的图象与x轴交于点A，求点A的坐标．
19．一次函数y=kx+b经过点A(3，2)和点B，其中点三是直线y=2x+1和y=x+4的交点，求这个一次函数的关系式，并画出图象．
20．在宽为6厘米的矩形纸带上，用菱形设计如下图所示的图案，如果菱形的边长为5厘米，请你回答下列问题：
(1)如果用5个这样的菱形设计图案，那么至少需要多长的纸带
(2)设菱形的个数为x，所需的纸带长为y，试求y和x之间的函数关系式；
(3)现有长为25厘米的纸带，要设计这样的图案，最多设计多少个菱形
21．如图，，分别表示A步行与B骑车在同一路上行驶的路程s(km)与时间t(h)的关系．
(1)B出发时与A相距______km；
(2)走了一段路后，自行车发生故障，进行修理，所用的时间是______h；
(3)B出发后______h与A相遇；
(4)若B的自行车不发生故障，保持出发时速度前进，______h与A相遇，相遇点离B的出发点______km．在图中表示出相遇点C；
(5)求出A行走的路程s与时间t的函数关系式．
22．一家小型放映厅的盈利额．y(元)同售票数x(张)之间的关系如图所示，其中保险部门规定：票数超过150张时，要缴纳公安消防保险费50元．试根据关系图，回答下列问题：
(1)试就0y(元)与x(张)之间的函数关系式；
(2)当售出的票数x为何值时，此放映厅不赔不赚 当售出的票数x满足何值时，此放映厅要赔本 当售出的票数x为何值时，此放映厅能赚钱
(3)当售出的票数x为何值时，此时所获得的利润比当x=150时多
参考答案
1.
C
2.
D
3.
C
4.
A
5.
D
6.
B
7.
B
8.
B
9.
D
10.
B
11.
A
12．(0，2)
13．C(2,
1)，D(，1)
14．1
15.
(2，2)或(2，)
16．
(8，4)
17．
(1，0)
18．(1)
P(3，6)在y=klx的图象上，
6=k1·3．
k1=2．
又P(3，6)在y=k2x9的图象上，
6=3k29，
k2=1
(2)由一次函数y=x9，得
图象与x轴交于点A，则0=x9,
x=9．
A
(9,
0)
19．由
得
B(1，3)．
Y=kx+b的图像经过A
(3，2)
B(1，3),
得
解得
y=．图象略．
(1)构造RtABC，如图：
AC=5，BC=3,
AB=4，6×4=24，需要24
cm的纸带．
(2)y=4(x+1)，即
y=4x+4．
(3)当y=25时，x=，最多设计5个菱形．
21．
(1)10
(2)1
(3)3
(4)B刚开始的速度==15
km／h．
若不发生故障B与A在l
h后相遇，相遇点离点B
15
km，相遇点C如图：
(5)设A行走路程s与时间t的函数关系为
s=kt+b，因过(0，10)，(3,
25)两点．故有10=b，25=3k+b，
k=5，b=10，s=5t+10．
22．(1)当0设y=klx+b1，
代入(100，0)和(0，200)，
得到
y=2x200．
当
150设y=k2x+b2，
代入(150，50)和(200，200)，
得
解得
y=3x400．
(2)当x=100时，此放映厅不赔不赚，
当0当1
00(3)当x=150时．y=100，在150当150时多