吉林省伊通满族自治县第三中学校人教A版高中数学必修一1.3.2奇偶性的概念 课件 (共35张PPT)
文档属性
| 名称 | 吉林省伊通满族自治县第三中学校人教A版高中数学必修一1.3.2奇偶性的概念 课件 (共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 680.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-10 14:21:51 | ||
图片预览











文档简介
课件35张PPT。第1课时 奇偶性的概念第一章 1.3.2 奇偶性1.理解函数奇偶性的定义;
2.掌握函数奇偶性的判断和证明方法;
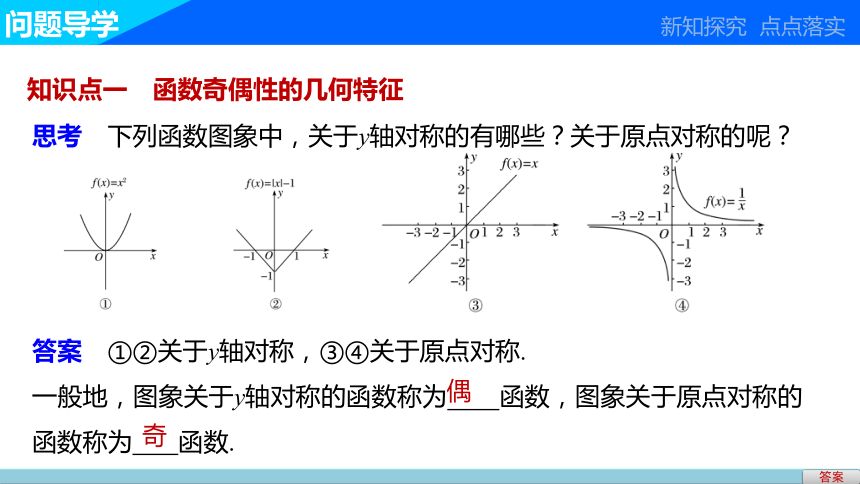
3.会应用奇、偶函数图象的对称性解决简单问题.问题导学题型探究达标检测学习目标问题导学 新知探究 点点落实知识点一 函数奇偶性的几何特征思考 下列函数图象中,关于y轴对称的有哪些?关于原点对称的呢?答案答案 ①②关于y轴对称,③④关于原点对称.一般地,图象关于y轴对称的函数称为 函数,图象关于原点对称的函数称为 函数.偶奇知识点二 函数奇偶性的定义思考1 为什么不直接用图象关于y轴(原点)对称来定义函数的奇偶性?答案答案 因为很多函数图象我们不知道,即使画出来,细微之处是否对称也难以精确判断.思考2 利用点对称来刻画图象对称有什么好处?答案 好处有两点:(1)等价:只要所有点均关于y轴(原点)对称,则图象关于y轴(原点)对称,反之亦然.(2)可操作:要判断点是否关于y轴(原点)对称,只要代入解析式验证即可,不知道函数图象也能操作.答案(1)偶函数:如果对于函数f(x)的定义域内 一个x,都有 ,那么函数f(x)就叫做偶函数.其实质是函数f(x)上任一点(x,f(x))关于y轴的对称点(-x,f(x))也在f(x)图象上.
(2)奇函数:如果对于函数f(x)的定义域内 一个x,都有
,那么函数f(x)就叫做奇函数.其实质是函数f(x)上任一点(x,f(x))关于原点的对称点(-x,-f(x))也在f(x)图象上.任意f(-x)=f(x)f(-x)=-f(x)任意函数奇偶性的概念:知识点三 奇(偶)函数的定义域特征思考 如果一个函数f(x)的定义域是(-1,1],那这个函数f(x)还具有奇偶性吗?答案答案 由函数奇偶性定义,对于定义域内任一元素x,其相反数-x必须也在定义域内,才能进一步判断f(-x)与f(x)的关系.而本问题中,1∈(-1,1],-1?(-1,1],f(-1)无定义,自然也谈不上是否与f(1)相等了.所以该函数既非奇函数,也非偶函数.返回答案一般地,判断函数奇偶性要注意定义域优先原则,即首先要看定义域是否关于 对称.原点题型探究 重点难点 个个击破类型一 如何证明函数的奇偶性证明 因为它的定义域为{x|x∈R且x≠1},
∴对于定义域内的-1,其相反数1不在定义域内,解析答案解析答案(2)证明f(x)=(x+1)(x-1)是偶函数;证明 函数的定义域为R,
因函数f(x)=(x+1)(x-1)=x2-1,
又因f(-x)=(-x)2-1=x2-1=f(x),
所以函数为偶函数.解析答案即该函数既是奇函数又是偶函数.解析答案证明 定义域为{x|x≠0}.
若x<0,则-x>0,∴f(-x)=1,f(x)=-1,
∴f(-x)=-f(x);
若x>0,则-x<0,∴f(-x)=-1,f(x)=1,
∴f(-x)=-f(x);
即对任意x≠0,都有f(-x)=-f(x).
∴f(x)为奇函数.解析答案(5)已知f(x)的定义域为R,证明g(x)=f(-x)+f(x)是偶函数.证明 ∵f(x)的定义域为R,
∴g(x)=f(-x)+f(x)的定义域也为R.
对于任意x∈R,都有g(-x)=f[-(-x)]+f(-x)=f(-x)+f(x)=g(x),
∴g(x)是偶函数.反思与感悟利用定义法判断函数是不是偶函数时,首先应看函数定义域是否关于原点对称,即对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量.解析答案解析答案(2)证明f(x)=x|x|是奇函数;证明 函数的定义域为R,因f(-x)=(-x)|-x|=-x|x|=-f(x),
所以函数为奇函数.解析答案因为对定义域内的每一个x,都有f(x)=0,所以f(-x)=f(x),即该函数既是奇函数又是偶函数.解析答案证明 定义域为{x|x≠0}.
若x<0,则-x>0,
∴f(-x)=x2,f(x)=-x2,∴f(-x)=-f(x);
若x>0,则-x<0,
∴f(-x)=-(-x)2=-x2,f(x)=x2,
∴f(-x)=-f(x);
即对任意x≠0,都有f(-x)=-f(x).
∴f(x)为奇函数.类型二 如何判断函数的奇偶性例2 (1)f(x),g(x)是定义在R上的奇函数,试判断y=f(x)+g(x),y=f(x)g(x),y=f[g(x)]的奇偶性;解析答案解 ∵f(x),g(x)是定义在R上的奇函数,
∴f(-x)+g(-x)=-f(x)-g(x)=-[f(x)+g(x)],y=f(x)+g(x)是奇函数.
f(-x)g(-x)=[-f(x)][-g(x)]=f(x)g(x),y=f(x)g(x)是偶函数.
f[g(-x)]=f[-g(x)]=-f[g(x)],y=f[g(x)]是奇函数.解析答案(2)判断f(x)=x3+3x的奇偶性;解 ∵y=x3,y=3x都是奇函数,由(1)知f(x)=x3+3x是奇函数.(3)已知函数f(x)=ax3+bx2+cx+d是奇函数,求实数b,d的值.解 由(1)知当b=d=0时,f(x)=ax3+bx2+cx+d是奇函数.反思与感悟判断函数单调性要比证明灵活得多,可以借助图象,也可借助已知奇偶性的函数,在此基础上判断其和、差、积、商复合的奇偶性.解析答案跟踪训练2 (1)f(x),g(x)定义在R上,f(x)是奇函数,g(x)是偶函数,试判断y=f(x)g(x),y=f [g(x)]的奇偶性;解 ∵f(x),g(x)定义在R上,f(x)是奇函数,g(x)是偶函数,
∴f(-x)g(-x)=-f(x)g(x),y=f(x)g(x)是奇函数.
f [g(-x)]=f [g(x)],y=f [g(x)]是偶函数.解析答案解析答案(3)已知f(x),g(x)均为奇函数,且F(x)=af(x)+bg(x)+2在(0,+∞)上有最大值5(ab≠0),求F(x)在(-∞,0)上的最小值.解 ∵f(x),g(x)均为奇函数,∴y=af(x)+bg(x)是奇函数.
设x<0,则-x>0.
由F(x)=af(x)+bg(x)+2在(0,+∞)上有最大值5(ab≠0),
∴F(-x)=af(-x)+bg(-x)+2≤5,
∴af(-x)+bg(-x)≤3,
∴af(x)+bg(x)≥-3,
∴af(x)+bg(x)+2≥-3+2=-1.
即F(x)在(-∞,0)上的最小值为-1.类型三 奇(偶)函数图象的对称性的应用例3 定义在R上的奇函数f(x)在[0,+∞)上的图象
如图所示.
(1)画出f(x)的图象;解析答案解 先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图象如下图,解析答案(2)解不等式xf(x)>0.解 xf(x)>0即图象上横坐标、纵坐标同号.
结合图象可知,xf(x)>0的解集是(-2,0)∪(0,2).反思与感悟鉴于奇(偶)函数图象关于原点(y轴)对称,可以用这一特性去画图、求值,求解析式,研究单调性.解析答案返回返回解 显然当x>0时,f(x)>0.
又y=x2+1为偶函数,y=x为奇函数,123达标检测 45答案1.函数f(x)=0(x∈R)是( )
A.奇函数
B.偶函数
C.非奇非偶函数
D.既是奇函数又是偶函数D12345答案A123453.函数f(x)=x(-1A.奇函数 B.偶函数
C.非奇非偶函数 D.既是奇函数又是偶函数答案C123454.已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于( )
A.4 B.3 C.2 D.1答案B123455.下列说法错误的个数是( )
①图象关于原点对称的函数是奇函数;
②图象关于y轴对称的函数是偶函数;
③奇函数的图象一定过原点;
④偶函数的图象一定与y轴相交;
⑤既是奇函数,又是偶函数的函数一定是f(x)=0(x∈R).
A.4 B.3 C.2 D.0答案B1.两个定义:对于f(x)定义域内的任意一个x,如果都有f(-x)=-f(x)?
f(-x)+f(x)=0?f(x)为奇函数;如果都有f(-x)=f(x)?f(-x)-f(x)=0?
f(x)为偶函数.
2.两个性质:函数为奇函数?它的图象关于原点对称;函数为偶函数?
它的图象关于y轴对称.
3.证明一个函数是奇函数,必须对f(x)的定义域内任意一个x,都有f(-x)
=-f(x).而证明一个函数不是奇函数,只要能举出一个反例就可以了.返回本课结束更多精彩内容请登录:www.91taoke.com
2.掌握函数奇偶性的判断和证明方法;
3.会应用奇、偶函数图象的对称性解决简单问题.问题导学题型探究达标检测学习目标问题导学 新知探究 点点落实知识点一 函数奇偶性的几何特征思考 下列函数图象中,关于y轴对称的有哪些?关于原点对称的呢?答案答案 ①②关于y轴对称,③④关于原点对称.一般地,图象关于y轴对称的函数称为 函数,图象关于原点对称的函数称为 函数.偶奇知识点二 函数奇偶性的定义思考1 为什么不直接用图象关于y轴(原点)对称来定义函数的奇偶性?答案答案 因为很多函数图象我们不知道,即使画出来,细微之处是否对称也难以精确判断.思考2 利用点对称来刻画图象对称有什么好处?答案 好处有两点:(1)等价:只要所有点均关于y轴(原点)对称,则图象关于y轴(原点)对称,反之亦然.(2)可操作:要判断点是否关于y轴(原点)对称,只要代入解析式验证即可,不知道函数图象也能操作.答案(1)偶函数:如果对于函数f(x)的定义域内 一个x,都有 ,那么函数f(x)就叫做偶函数.其实质是函数f(x)上任一点(x,f(x))关于y轴的对称点(-x,f(x))也在f(x)图象上.
(2)奇函数:如果对于函数f(x)的定义域内 一个x,都有
,那么函数f(x)就叫做奇函数.其实质是函数f(x)上任一点(x,f(x))关于原点的对称点(-x,-f(x))也在f(x)图象上.任意f(-x)=f(x)f(-x)=-f(x)任意函数奇偶性的概念:知识点三 奇(偶)函数的定义域特征思考 如果一个函数f(x)的定义域是(-1,1],那这个函数f(x)还具有奇偶性吗?答案答案 由函数奇偶性定义,对于定义域内任一元素x,其相反数-x必须也在定义域内,才能进一步判断f(-x)与f(x)的关系.而本问题中,1∈(-1,1],-1?(-1,1],f(-1)无定义,自然也谈不上是否与f(1)相等了.所以该函数既非奇函数,也非偶函数.返回答案一般地,判断函数奇偶性要注意定义域优先原则,即首先要看定义域是否关于 对称.原点题型探究 重点难点 个个击破类型一 如何证明函数的奇偶性证明 因为它的定义域为{x|x∈R且x≠1},
∴对于定义域内的-1,其相反数1不在定义域内,解析答案解析答案(2)证明f(x)=(x+1)(x-1)是偶函数;证明 函数的定义域为R,
因函数f(x)=(x+1)(x-1)=x2-1,
又因f(-x)=(-x)2-1=x2-1=f(x),
所以函数为偶函数.解析答案即该函数既是奇函数又是偶函数.解析答案证明 定义域为{x|x≠0}.
若x<0,则-x>0,∴f(-x)=1,f(x)=-1,
∴f(-x)=-f(x);
若x>0,则-x<0,∴f(-x)=-1,f(x)=1,
∴f(-x)=-f(x);
即对任意x≠0,都有f(-x)=-f(x).
∴f(x)为奇函数.解析答案(5)已知f(x)的定义域为R,证明g(x)=f(-x)+f(x)是偶函数.证明 ∵f(x)的定义域为R,
∴g(x)=f(-x)+f(x)的定义域也为R.
对于任意x∈R,都有g(-x)=f[-(-x)]+f(-x)=f(-x)+f(x)=g(x),
∴g(x)是偶函数.反思与感悟利用定义法判断函数是不是偶函数时,首先应看函数定义域是否关于原点对称,即对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量.解析答案解析答案(2)证明f(x)=x|x|是奇函数;证明 函数的定义域为R,因f(-x)=(-x)|-x|=-x|x|=-f(x),
所以函数为奇函数.解析答案因为对定义域内的每一个x,都有f(x)=0,所以f(-x)=f(x),即该函数既是奇函数又是偶函数.解析答案证明 定义域为{x|x≠0}.
若x<0,则-x>0,
∴f(-x)=x2,f(x)=-x2,∴f(-x)=-f(x);
若x>0,则-x<0,
∴f(-x)=-(-x)2=-x2,f(x)=x2,
∴f(-x)=-f(x);
即对任意x≠0,都有f(-x)=-f(x).
∴f(x)为奇函数.类型二 如何判断函数的奇偶性例2 (1)f(x),g(x)是定义在R上的奇函数,试判断y=f(x)+g(x),y=f(x)g(x),y=f[g(x)]的奇偶性;解析答案解 ∵f(x),g(x)是定义在R上的奇函数,
∴f(-x)+g(-x)=-f(x)-g(x)=-[f(x)+g(x)],y=f(x)+g(x)是奇函数.
f(-x)g(-x)=[-f(x)][-g(x)]=f(x)g(x),y=f(x)g(x)是偶函数.
f[g(-x)]=f[-g(x)]=-f[g(x)],y=f[g(x)]是奇函数.解析答案(2)判断f(x)=x3+3x的奇偶性;解 ∵y=x3,y=3x都是奇函数,由(1)知f(x)=x3+3x是奇函数.(3)已知函数f(x)=ax3+bx2+cx+d是奇函数,求实数b,d的值.解 由(1)知当b=d=0时,f(x)=ax3+bx2+cx+d是奇函数.反思与感悟判断函数单调性要比证明灵活得多,可以借助图象,也可借助已知奇偶性的函数,在此基础上判断其和、差、积、商复合的奇偶性.解析答案跟踪训练2 (1)f(x),g(x)定义在R上,f(x)是奇函数,g(x)是偶函数,试判断y=f(x)g(x),y=f [g(x)]的奇偶性;解 ∵f(x),g(x)定义在R上,f(x)是奇函数,g(x)是偶函数,
∴f(-x)g(-x)=-f(x)g(x),y=f(x)g(x)是奇函数.
f [g(-x)]=f [g(x)],y=f [g(x)]是偶函数.解析答案解析答案(3)已知f(x),g(x)均为奇函数,且F(x)=af(x)+bg(x)+2在(0,+∞)上有最大值5(ab≠0),求F(x)在(-∞,0)上的最小值.解 ∵f(x),g(x)均为奇函数,∴y=af(x)+bg(x)是奇函数.
设x<0,则-x>0.
由F(x)=af(x)+bg(x)+2在(0,+∞)上有最大值5(ab≠0),
∴F(-x)=af(-x)+bg(-x)+2≤5,
∴af(-x)+bg(-x)≤3,
∴af(x)+bg(x)≥-3,
∴af(x)+bg(x)+2≥-3+2=-1.
即F(x)在(-∞,0)上的最小值为-1.类型三 奇(偶)函数图象的对称性的应用例3 定义在R上的奇函数f(x)在[0,+∞)上的图象
如图所示.
(1)画出f(x)的图象;解析答案解 先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图象如下图,解析答案(2)解不等式xf(x)>0.解 xf(x)>0即图象上横坐标、纵坐标同号.
结合图象可知,xf(x)>0的解集是(-2,0)∪(0,2).反思与感悟鉴于奇(偶)函数图象关于原点(y轴)对称,可以用这一特性去画图、求值,求解析式,研究单调性.解析答案返回返回解 显然当x>0时,f(x)>0.
又y=x2+1为偶函数,y=x为奇函数,123达标检测 45答案1.函数f(x)=0(x∈R)是( )
A.奇函数
B.偶函数
C.非奇非偶函数
D.既是奇函数又是偶函数D12345答案A123453.函数f(x)=x(-1
C.非奇非偶函数 D.既是奇函数又是偶函数答案C123454.已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于( )
A.4 B.3 C.2 D.1答案B123455.下列说法错误的个数是( )
①图象关于原点对称的函数是奇函数;
②图象关于y轴对称的函数是偶函数;
③奇函数的图象一定过原点;
④偶函数的图象一定与y轴相交;
⑤既是奇函数,又是偶函数的函数一定是f(x)=0(x∈R).
A.4 B.3 C.2 D.0答案B1.两个定义:对于f(x)定义域内的任意一个x,如果都有f(-x)=-f(x)?
f(-x)+f(x)=0?f(x)为奇函数;如果都有f(-x)=f(x)?f(-x)-f(x)=0?
f(x)为偶函数.
2.两个性质:函数为奇函数?它的图象关于原点对称;函数为偶函数?
它的图象关于y轴对称.
3.证明一个函数是奇函数,必须对f(x)的定义域内任意一个x,都有f(-x)
=-f(x).而证明一个函数不是奇函数,只要能举出一个反例就可以了.返回本课结束更多精彩内容请登录:www.91taoke.com
