江苏省兴化一中2017-2018学年高一上学期第一次月考数学试卷 Word版含答案
文档属性
| 名称 | 江苏省兴化一中2017-2018学年高一上学期第一次月考数学试卷 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 568.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-10 14:37:23 | ||
图片预览




文档简介
兴化市第一中学2017年秋学期
第一次月考高一数学试卷
2017.10.8
说明:本试卷共20小题,满分160分,考试时间120分钟.
一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答题纸中的横线上,答在试卷上的无效.
1.设集合,则
▲
2.写出集合的所有子集__
▲
3.因式分解:=
▲
4.一元二次不等式的解集为
▲
5.已知集合,那么集合=___▲___
6.函数的定义域为
▲
7.函数的值域是
▲
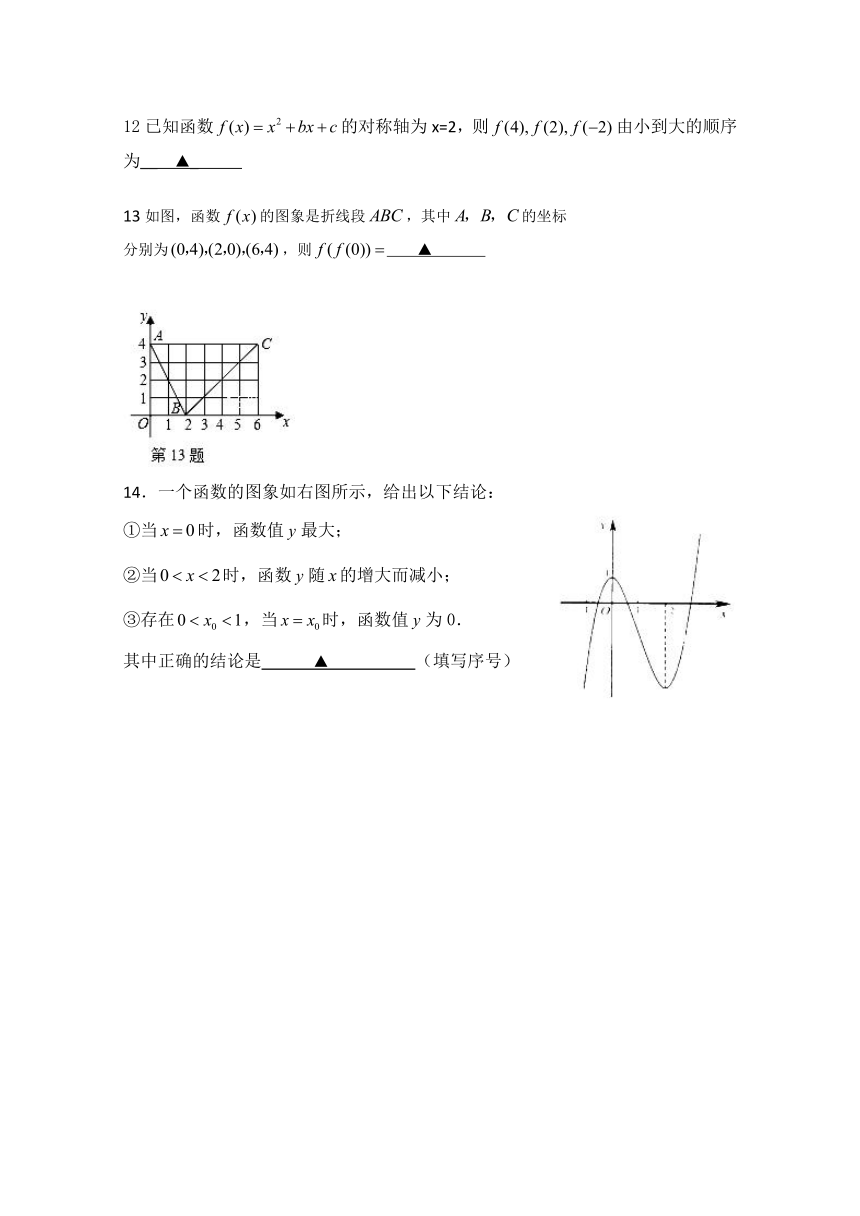
8.下列图象中表示函数关系的有
▲
(填序号)
9.集合用列举法表示为
▲
10.在内部有一点,且,
则点为的
▲
(从“重心、垂心、内心、外心”中选一个作答)
11设全集U={1,2,3,4,5,6,7,8},A=
{1,2,3
},B={3,4,5,6}则图中阴影部分所表示的集合为
▲
12已知函数的对称轴为x=2,则由小到大的顺序为__
▲_
13如图,函数的图象是折线段,其中的坐标
分别为,则
▲
14.一个函数的图象如右图所示,给出以下结论:
①当时,函数值最大;
②当时,函数随的增大而减小;
③存在,当时,函数值为0.
其中正确的结论是
▲
(填写序号)
兴化市第一中学2017年秋学期
第一次月考
高一数学
答题纸
2017.10.8
一、填空题(5′×14
=
70′)
1、__________________
2、__________________
3、________________
4、__________________
5、__________________
6、________________
7、__________________
8、__________________
9、________________
10、_________________
11、_________________
12、_______________
13、_________________
14、_________________
二、解答题:本大题共6个小题,共90分.写出必要的文字说明、演算步骤和证明过程.
15.(1)已知全集U={2,a2+9a+3,6},A={2,|a+3|}, UA={3},求实数a的值
(2)设全集U={1,2,3,4},且={
|
,U},若={2,3},求m的值.
16.全集,若集合,则(结果用区间表示)
(1)求
(2)若集合,求的取值范围
17
解方程组
(1)
(2)
18已知函数
(1)用分段函数的形式表示;(2)画出函数的图像,写出函数的值域。
19某民营企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图甲,B产品的利润与投资的算术平方根成正比,其关系如图乙(注:利润与投资单位:万元).
(1)分别将A、B两种产品的利润表示为投资(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元
20.(16分)设,,
(1)
A=
A,求a的值(2)
A,且A
=,求a的值(3)
A
=
A,求a的值.
兴化市第一中学2017年秋学期
第一次月考高一数学试卷
2017.10.8
说明:本试卷共20小题,满分160分,考试时间120分钟.
一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答题纸中的横线上,答在试卷上的无效.
1.设集合,则
2.写出集合的所有子集__
,,,
3.因式分解:=
4.一元二次不等式的解集为
5.已知集合,那么集合=__________
6.函数的定义域为
7.函数的值域是
.
8.下列图象中表示函数关系的有
(填序号).(1)
9.集合用列举法表示为
▲
10.在内部有一点,且,则点为的
.(从“重心、垂心、内心、外心”中选一个作答)
外心
11设全集U={1,2,3,4,5,6,7,8},A=
{1,2,3
},B={3,4,5,6}则图中阴影部分所表示的集合为
{7,8
}
12已知函数的对称轴为x=2,则由小到大的顺序为___
13如图,函数的图象是折线段,其中的坐标
分别为,则
2
14.一个函数的图象如右图所示,给出以下结论:
①当时,函数值最大;
②当时,函数随的增大而减小;
③存在,当时,函数值为0.
其中正确的结论是
(填写序号).
②③
二、解答题:本大题共6个小题,共90分.写出必要的文字说明、演算步骤和证明过程.
15.(1)已知全集U={2,a2+9a+3,6},A={2,|a+3|}, UA={3},求实数a的值
(2)设全集U={1,2,3,4},且={
|
,U},若={2,3},求m的值.
(1)解:∵A∪(CUA)=U,∴{2,3,|a+3|}={2,a2+9a+3,6},
则,即,解得a=﹣9,
经验证a=﹣9符合题意,所以a的值是﹣9.
(2)解:∵U={1,2,3,4},CUA={2,3},∴1,4∈A,
∴由根与系数之间的关系得m=1×4=4,故m=4.
16.全集,若集合,则(结果用区间表示)
(1)求
(2)若集合,求的取值范围
解:(1)求
(2)
17
解方程组
(1)
(2)
解:
(1)
所以原方程组的解是
说明:在解类似于本例的二元二次方程组时,通常采用本例所介绍的代入消元法来求解.
(2)
解法二:对这个方程组,也可以根据一元二次方程的根与系数的关系,把看作一个一元二次方程的两个根,通过解这个一元二次方程来求.这个方程组的是一元二次方程
的两个根,解这个方程,得,或.
所以原方程组的解是
18已知函数
(1)用分段函数的形式表示;(2)画出函数的图像,写出函数的值域。
解:(1)∵当x≥﹣3时,|x+3|=x+3,f(x)=|x+3|+x﹣5=2x﹣2;
当x<﹣3时,|x+3|=﹣x﹣3,f(x)=|x+3|+x﹣5=﹣8
因此,用分段函数的形式表示函数,
可得f(x)=;
(2)画出函数的图象,如右图所示,
根据图象,可得函数的值域为[﹣8,+∞).
【点评】本题给出带绝对值的函数,求函数的分段形式的表达式并求函数的值域.着重考查了绝对值的意义、函数图象的作法和函数的值域,属于中档题.
19某民营企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图甲,B产品的利润与投资的算术平方根成正比,其关系如图乙(注:利润与投资单位:万元).
甲
乙
(1)分别将A、B两种产品的利润表示为投资(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元
解:
(1)
设投资为x万元,A产品的利润为f(x)万元,B产品的利润为g(x)万元
由题设,由图知f(1)=,故k1=
。又。
从而.………6分
(2)
设A产品投入x万元,则B产品投入10-x万元,设企业利润为y万元
………9分
令则………13分
当。………14分
答:
当A产品投入3.75万元,则B产品投入6.25万元,企业最大利润为万元.
20.(16分)设,,.(1)A=
A,求a的值(2)
A,且A
=,求a的值(3)
A
=
A
,求a的值.
解:(1)∵A=
A,∴A=B
,
∴
解得a=5.
(2)B={2,3},C={2,-4}.
∵
A,
∴A
.
∵A
=∴2A,-4A.
∴3∈A.
将x=3代入A中的方程得a=5或a=-2,
a=5时A={2,3},不合题意.
∴a=-2.
(3)∵A
=
A
,
∴A
=
A
={2},
∴2∈A.
将x=2代入A中的方程得a=5或a=-3
.
a=5时经检验A
A,舍去.
∴a=-3.
第13题
2
B
C
A
y
x
1
O
3
4
5
6
1
2
3
4
PAGE
第一次月考高一数学试卷
2017.10.8
说明:本试卷共20小题,满分160分,考试时间120分钟.
一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答题纸中的横线上,答在试卷上的无效.
1.设集合,则
▲
2.写出集合的所有子集__
▲
3.因式分解:=
▲
4.一元二次不等式的解集为
▲
5.已知集合,那么集合=___▲___
6.函数的定义域为
▲
7.函数的值域是
▲
8.下列图象中表示函数关系的有
▲
(填序号)
9.集合用列举法表示为
▲
10.在内部有一点,且,
则点为的
▲
(从“重心、垂心、内心、外心”中选一个作答)
11设全集U={1,2,3,4,5,6,7,8},A=
{1,2,3
},B={3,4,5,6}则图中阴影部分所表示的集合为
▲
12已知函数的对称轴为x=2,则由小到大的顺序为__
▲_
13如图,函数的图象是折线段,其中的坐标
分别为,则
▲
14.一个函数的图象如右图所示,给出以下结论:
①当时,函数值最大;
②当时,函数随的增大而减小;
③存在,当时,函数值为0.
其中正确的结论是
▲
(填写序号)
兴化市第一中学2017年秋学期
第一次月考
高一数学
答题纸
2017.10.8
一、填空题(5′×14
=
70′)
1、__________________
2、__________________
3、________________
4、__________________
5、__________________
6、________________
7、__________________
8、__________________
9、________________
10、_________________
11、_________________
12、_______________
13、_________________
14、_________________
二、解答题:本大题共6个小题,共90分.写出必要的文字说明、演算步骤和证明过程.
15.(1)已知全集U={2,a2+9a+3,6},A={2,|a+3|}, UA={3},求实数a的值
(2)设全集U={1,2,3,4},且={
|
,U},若={2,3},求m的值.
16.全集,若集合,则(结果用区间表示)
(1)求
(2)若集合,求的取值范围
17
解方程组
(1)
(2)
18已知函数
(1)用分段函数的形式表示;(2)画出函数的图像,写出函数的值域。
19某民营企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图甲,B产品的利润与投资的算术平方根成正比,其关系如图乙(注:利润与投资单位:万元).
(1)分别将A、B两种产品的利润表示为投资(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元
20.(16分)设,,
(1)
A=
A,求a的值(2)
A,且A
=,求a的值(3)
A
=
A,求a的值.
兴化市第一中学2017年秋学期
第一次月考高一数学试卷
2017.10.8
说明:本试卷共20小题,满分160分,考试时间120分钟.
一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答题纸中的横线上,答在试卷上的无效.
1.设集合,则
2.写出集合的所有子集__
,,,
3.因式分解:=
4.一元二次不等式的解集为
5.已知集合,那么集合=__________
6.函数的定义域为
7.函数的值域是
.
8.下列图象中表示函数关系的有
(填序号).(1)
9.集合用列举法表示为
▲
10.在内部有一点,且,则点为的
.(从“重心、垂心、内心、外心”中选一个作答)
外心
11设全集U={1,2,3,4,5,6,7,8},A=
{1,2,3
},B={3,4,5,6}则图中阴影部分所表示的集合为
{7,8
}
12已知函数的对称轴为x=2,则由小到大的顺序为___
13如图,函数的图象是折线段,其中的坐标
分别为,则
2
14.一个函数的图象如右图所示,给出以下结论:
①当时,函数值最大;
②当时,函数随的增大而减小;
③存在,当时,函数值为0.
其中正确的结论是
(填写序号).
②③
二、解答题:本大题共6个小题,共90分.写出必要的文字说明、演算步骤和证明过程.
15.(1)已知全集U={2,a2+9a+3,6},A={2,|a+3|}, UA={3},求实数a的值
(2)设全集U={1,2,3,4},且={
|
,U},若={2,3},求m的值.
(1)解:∵A∪(CUA)=U,∴{2,3,|a+3|}={2,a2+9a+3,6},
则,即,解得a=﹣9,
经验证a=﹣9符合题意,所以a的值是﹣9.
(2)解:∵U={1,2,3,4},CUA={2,3},∴1,4∈A,
∴由根与系数之间的关系得m=1×4=4,故m=4.
16.全集,若集合,则(结果用区间表示)
(1)求
(2)若集合,求的取值范围
解:(1)求
(2)
17
解方程组
(1)
(2)
解:
(1)
所以原方程组的解是
说明:在解类似于本例的二元二次方程组时,通常采用本例所介绍的代入消元法来求解.
(2)
解法二:对这个方程组,也可以根据一元二次方程的根与系数的关系,把看作一个一元二次方程的两个根,通过解这个一元二次方程来求.这个方程组的是一元二次方程
的两个根,解这个方程,得,或.
所以原方程组的解是
18已知函数
(1)用分段函数的形式表示;(2)画出函数的图像,写出函数的值域。
解:(1)∵当x≥﹣3时,|x+3|=x+3,f(x)=|x+3|+x﹣5=2x﹣2;
当x<﹣3时,|x+3|=﹣x﹣3,f(x)=|x+3|+x﹣5=﹣8
因此,用分段函数的形式表示函数,
可得f(x)=;
(2)画出函数的图象,如右图所示,
根据图象,可得函数的值域为[﹣8,+∞).
【点评】本题给出带绝对值的函数,求函数的分段形式的表达式并求函数的值域.着重考查了绝对值的意义、函数图象的作法和函数的值域,属于中档题.
19某民营企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图甲,B产品的利润与投资的算术平方根成正比,其关系如图乙(注:利润与投资单位:万元).
甲
乙
(1)分别将A、B两种产品的利润表示为投资(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元
解:
(1)
设投资为x万元,A产品的利润为f(x)万元,B产品的利润为g(x)万元
由题设,由图知f(1)=,故k1=
。又。
从而.………6分
(2)
设A产品投入x万元,则B产品投入10-x万元,设企业利润为y万元
………9分
令则………13分
当。………14分
答:
当A产品投入3.75万元,则B产品投入6.25万元,企业最大利润为万元.
20.(16分)设,,.(1)A=
A,求a的值(2)
A,且A
=,求a的值(3)
A
=
A
,求a的值.
解:(1)∵A=
A,∴A=B
,
∴
解得a=5.
(2)B={2,3},C={2,-4}.
∵
A,
∴A
.
∵A
=∴2A,-4A.
∴3∈A.
将x=3代入A中的方程得a=5或a=-2,
a=5时A={2,3},不合题意.
∴a=-2.
(3)∵A
=
A
,
∴A
=
A
={2},
∴2∈A.
将x=2代入A中的方程得a=5或a=-3
.
a=5时经检验A
A,舍去.
∴a=-3.
第13题
2
B
C
A
y
x
1
O
3
4
5
6
1
2
3
4
PAGE
同课章节目录
