第1章 反比例函数单元过关检测A卷

21世纪教育网 –中小学教育资源及组卷应用平台
反比例函数单元过关检测A卷
考号_______姓名___________总分________
一、选择题（每题4分，共48分）
1. 对于函数y=﹣，当x＜0时，函数图像位于（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 若点（﹣5，y1），（﹣3，y2），（3，y3）都在反比例函数y=图象上，则（ ）
A.y1＞y2＞y3 B.y2＞y1＞y3 C.y3＞y1＞y2 D.y1＞y3＞y2
3. 点A为反比例函数图象上一点，它到原点的距离为5，则x轴的距离为3，若点A第二象限内，则这个函数的解析式为（ ）
A、y= B、y=﹣ C、y= D、y=﹣
4. 已知反比例函数y=，在下列结论中，不正确的是（ ）
A．图象必经过点（1，2） B．y随x的增大而减少
C．图象在第一、三象限 D．若x＞1，则y＜2
5. 函数y= （k≠0，x＞0）的图象如下图，若z=，则z关于x的函数图象可能为（ ）
A． B． C． D．
6. 若函数为反比例函数，则m的值为（　　）
A．±1 B．1 C． D．﹣1
7. 如图，点A是双曲线y= 在第二象限分支上的任意一点，点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点．若四边形ABCD的面积是8，则k的值为（ ）
A.﹣1 B.1 C.2 D.﹣2
8. 某闭合电路中，电源的电压为定值，电流I（A）与电阻R（Ω）成反比例．如图所示的是该电路中电流I与电阻R之间的函数关系的图象，则用电阻R表示电流I的函数解析式为（ ）
A． I= B．I= C．I= D．I=
9. 正比例函数y=2x和反比例函数y=的一个交点为（1，2），则另一个交点为（ ）
A．（-1，-2） B．（-2，-1） C．（1，2） D．（2，1）
10. 下列函数中，y与x成反比例函数关系的是（ ）
A.x（y-1）=1 B.y= C.y= D.y=
11.如图，反比例函数y=的图象经过点A(-1,-2).则当x＞1时，函数值y的取值范围是（ ）
A、y＞1 B、0＜y＜1 C、y＞2 D、0＜ y＜2
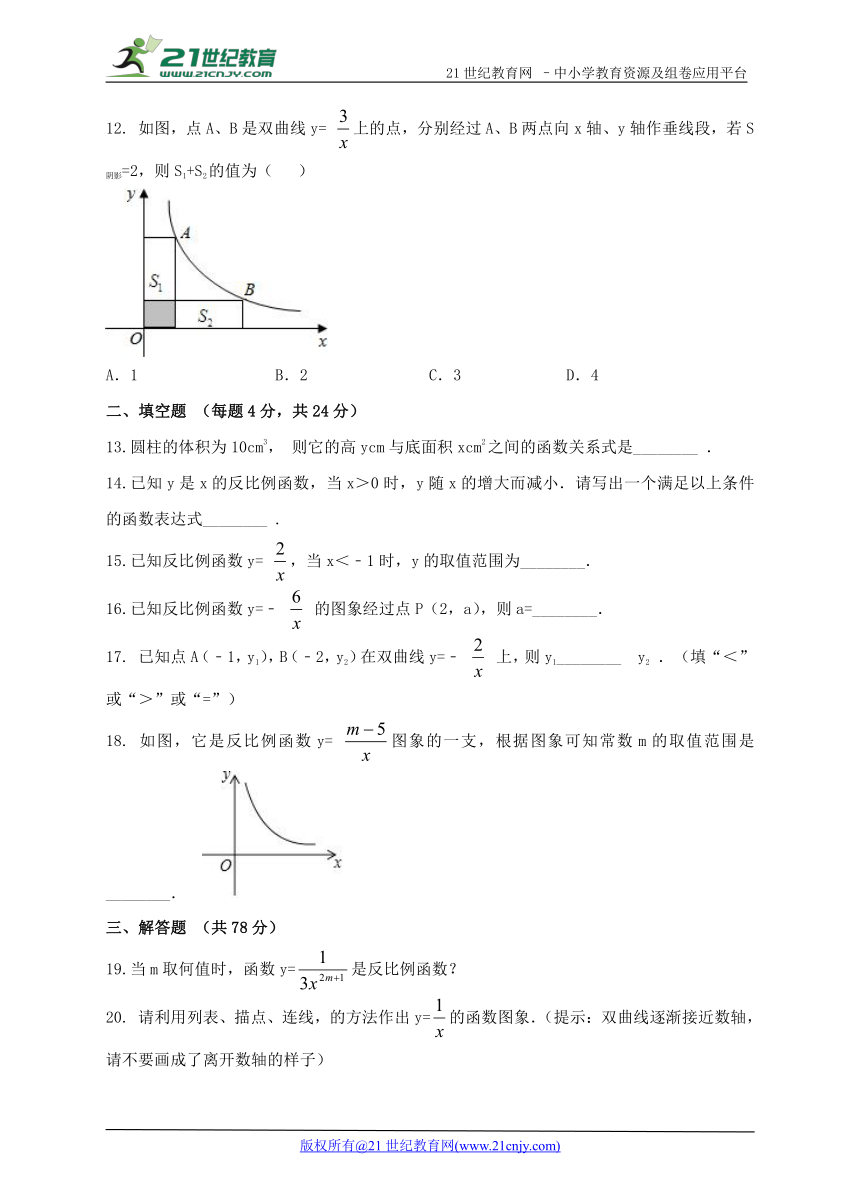
12. 如图，点A、B是双曲线y= 上的点，分别经过A、B两点向x轴、y轴作垂线段，若S阴影=2，则S1+S2的值为（ ）
A．1 B．2 C．3 D．4
二、填空题 （每题4分，共24分）
13.圆柱的体积为10cm3， 则它的高ycm与底面积xcm2之间的函数关系式是________ ．
14.已知y是x的反比例函数，当x＞0时，y随x的增大而减小．请写出一个满足以上条件的函数表达式________ .
15.已知反比例函数y= ，当x＜﹣1时，y的取值范围为________．
16.已知反比例函数y=﹣ 的图象经过点P（2，a），则a=________．
17. 已知点A（﹣1，y1），B（﹣2，y2）在双曲线y=﹣ 上，则y1________ y2 ． （填“＜”或“＞”或“=”）
18. 如图，它是反比例函数y= 图象的一支，根据图象可知常数m的取值范围是________．
三、解答题 （共78分）
19.当m取何值时，函数y=是反比例函数？
20. 请利用列表、描点、连线，的方法作出y=的函数图象．（提示：双曲线逐渐接近数轴，请不要画成了离开数轴的样子）
21. 已知函数y=和函数y=2x-1的图象都经过点（m，2 ）．
（1）求m、k的值；（2）求两图象的另一交点．
22. 已知反比例函数y= (k为常数，k≠2）
（1）若在这个函数图象的每一支上，y随x增大而增大，求k的取值范围；
（2）若P（-1，a）既在函数y=-2x+4的图象上，又在反比例函数图象上，求反比例函数的解析式．
23. 如图，一次函数x=2与反比例函数y=和y=-的图象分别交于A、B两点，若P是y轴上任意一点，求△PAB的面积．
24. 如图，反比例函数y=的图象过点A（-2，m），AB⊥x轴于点B，且S△AOB=3，求k和m的值．
25. 阅读并解答问题：
在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成矩形的周长与面积的数值相等，则这个点叫做谐点．例如：图中过点P分别作x轴，y轴的垂线，与坐标轴围成矩形OAPB的周长与面积的数值相等，则点P是和谐点．
（1）判断点M（1，2），N（4，4）是否为和谐点，并说明理由；
（2）若和谐点P（a，3）在双曲线y=，求a，b的值．
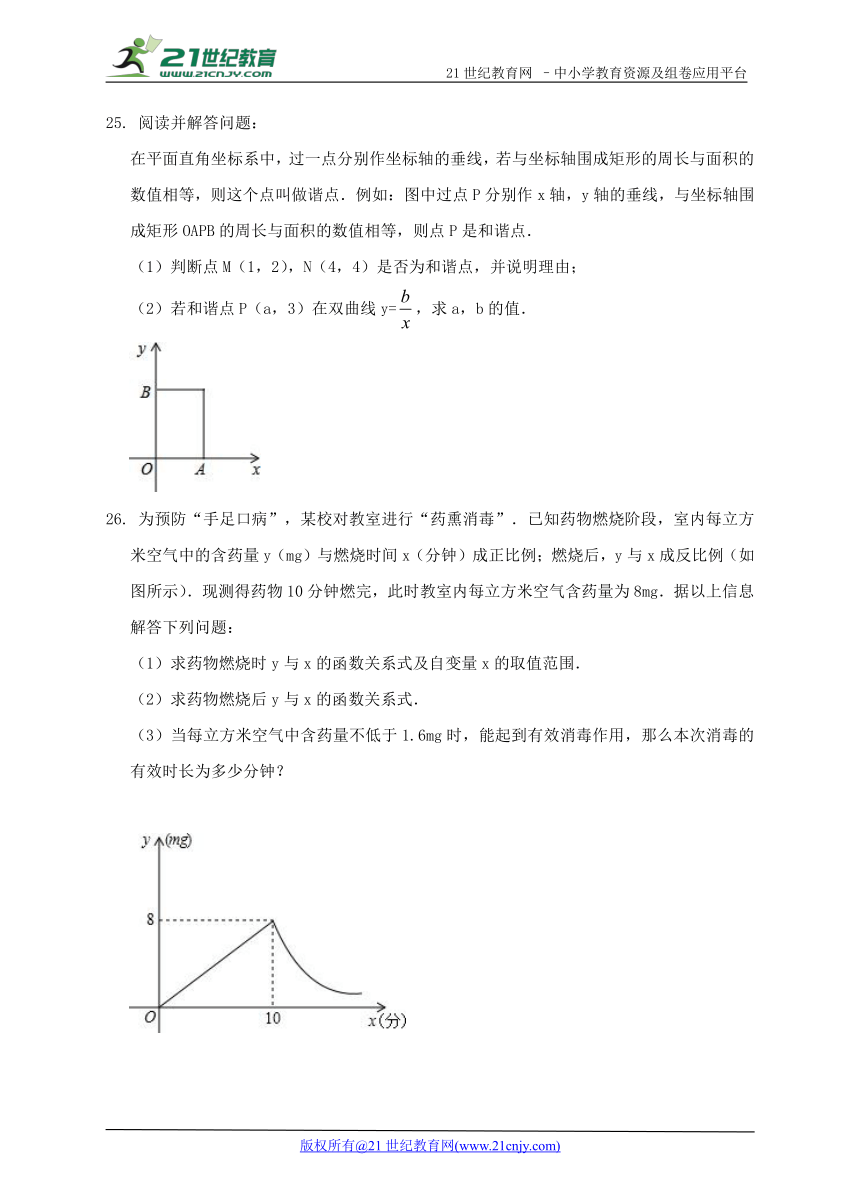
26. 为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（分钟）成正比例；燃烧后，y与x成反比例（如图所示）．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．据以上信息解答下列问题：
（1）求药物燃烧时y与x的函数关系式及自变量x的取值范围．
（2）求药物燃烧后y与x的函数关系式．
（3）当每立方米空气中含药量不低于1.6mg时，能起到有效消毒作用，那么本次消毒的有效时长为多少分钟？
答案解析
一、选择题
1、【分析】根据比例系数确定反比例函数的图像的位置，然后根据自变量的取值范围确定正确的选项即可．
解：∵反比例函数的比例系数为﹣3＜0， ∴反比例函数的图像位于二、四象限，
∵x＜0，
∴反比例函数位于第二象限，
故选B．
2、【分析】根据反比例函数图象上点的坐标特征，分别计算出y2、y1、y3的值，然后比较大小即可．
解：当x=﹣5时，y1=﹣ 25 ；当x=﹣3时，y2=﹣ 23 ；当x=3时，y3= 23 ， 所以y2＜y1＜y3 ．
故选C．
3、【分析】先设A点坐标为（x，y），根据A点到x轴的距离为3，得出y=±3，根据A点到原点的距离为5，得出x=±4，从而根据点A的位置确定点A的坐标，再设这个反比例函数的解析式为y= kx ，再把已知点A的坐标代入可求出k值，即得到反比例函数的解析式．
解：设A点坐标为（x，y）． ∵A点到x轴的距离为3，∴|y|=3，y=±3．
∵A点到原点的距离为5，∴x2+y2=52 ，
解得x=±4，
∵点A在第二象限，
∴x=﹣4，
∴点A的坐标为（﹣4，3），
设反比例函数的解析式为y= ，
∴k=﹣4×3=﹣12，
∴反比例函数的解析式为y=﹣ ，
故选B．
4、【分析】 根据反比例函数的性质对四个选项进行逐一分析即可．
解：A、∵1×2=2，∴图象必经过点（1，2），故本选项正确；
B、∵反比例函数y=中，k=2＞0，∴此函数的图象在每一象限内y随x的增大而减小，故本选项正确；
C、∵反比例函数y=中，k=2＞0，∴此函数的图象在一、三象限，故本选项正确；
D、∵当x＞1时，此函数图象在第一象限，∴0＜y＜2，故本选项错误．
故选D．
5、【分析】根据反比例函数解析式以及z=，即可找出z关于x的函数解析式，再根据反比例函数图象在第一象限可得出k＞0，结合x的取值范围即可得出结论．
解：∵y=（k≠0，x＞0），
∴z===（k≠0，x＞0）．
∵反比例函数y=（k≠0，x＞0）的图象在第一象限，
∴k＞0，
∴＞0．
∴z关于x的函数图象为第一象限内，且不包括原点的正比例的函数图象．
故选D．
6、【分析】根据反比例函数的定义即可求出m的值．
解：根据题意得：m2﹣2=﹣1，且m﹣1≠0
解得：m=﹣1．
故选D．
7、【分析】先判定出四边形ABCD是矩形，再根据反比例函数的系数的几何意义，用k表示出四边形ABCD的面积，然后求解即可．
解：∵点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点，
∴四边形ABCD是矩形，
∵四边形ABCD的面积是8，
∴4×|﹣k|=8，
解得|k|=2，
又∵双曲线位于第二、四象限，
∴k＜0，
∴k=﹣2．
故选D．
8、【分析】 观察图象，函数经过一定点，将此点坐标代入函数解析式（k≠0）即可求得k的值．
解：设反比例函数的解析式为（k≠0），
由图象可知，函数经过点B（3，2），
∴2=，得k=6，
∴反比例函数解析式为y=．
即用电阻R表示电流I的函数解析式为I=．
故选D．
9、【分析】根据反比例函数的关于原点对称的性质知，正比例函数y=2x和反比例函数的另一个交点与点（1，2）关于原点对称．
解：∵正比例函数y=2x和反比例函数y=的一个交点为（1，2），
∴另一个交点与点（1，2）关于原点对称，
∴另一个交点是（-1，-2）．
故选A．
10、【分析】此题应根据反比例函数的定义，解析式符合y=（k≠0)的形式为反比例函数．
解：A，B，C都不符合反比例函数的定义，错误；
D符合反比例函数的定义，正确．
故选D．
11、【分析】先根据反比例函数的图象过点A（-1，-2)，利用数形结合求出x＜-1时y的取值范围，再由反比例函数的图象关于原点对称的特点即可求出答案．
解：∵反比例函数的图象过点A（-1，-2)，
∴由函数图象可知，x＜-1时，-2＜y＜0，
∴当x＞1时，0＜y＜2．
故选：D．
12、【分析】先根据反比例函数系数k的几何意义求出S1+S阴影及S2+S阴影的值，进而可得出S1+S2的值．
解：∵点A、B是双曲线y=上的点，
∴S1+S阴影=S2+S阴影=3，
∴S1+S2=6-2S阴影=6-4=2．
故选B．
二、填空题
13、【分析】根据圆柱体的体积计算方法：底面积×高=体积可得xy=10，进而可得答案．
解：由题意得：xy=10，
则y= ，
故答案为：y= ．
14、【分析】反比例函数的图象在每个象限内，函数值y随自变量x的增大而增大，则反比例函数的反比例系数k＜0；反之，只要k＜0，则反比例函数在每个象限内，函数值y随自变量x的增大而增大．
解：只要使反比例系数大于0即可．如y=（x＞0），答案不唯一．
故答案为： （x＞0），答案不唯一．
15、【分析】先根据反比例函数的性质判断出函数的增减性，再求出x=﹣1时y的值即可得出结论．
解：∵反比例函数y= 中，k=2＞0， ∴此函数图象的两个分支位于一、三象限，且在每一象限内y随x的增大而减小，
∵当x=﹣1时，y=﹣2，
∴当x＜﹣1时，﹣2＜y＜0．
故答案为：﹣2＜y＜0．
16、【分析】根据反比例函数图象上点的坐标特征，将坐标代入即可得出a的值．
解：把点P（2，a）代入反比例函数y=﹣ 6x 中，a=﹣3． 故答案为﹣3．
17、【分析】根据反比例函数图象上的点的坐标特点，可以利用函数解析式计算出y1=2，y2=1，进而可得答案．
解：∵点A（﹣1，y1），B（﹣2，y2）在双曲线y=﹣ 上，
∴﹣1 y1=﹣2，﹣2 y2=﹣2，
解得：y1=2，y2=1，
∴y1＞y2 ，
故答案为：＞．
18、【分析】根据图象可知反比例函数中m﹣5＞0，从而可以求得m的取值范围，本题得以解决．
解：由图象可知， 反比例函数y= 图象在第一象限，
∴m﹣5＞0，得m＞5，
故答案为：m＞5．
三、解答题
19、【分析】根据反比例函数的定义．即y=（k≠0），只需令2m+1=1即可．
解：∵函数是反比例函数，
∴2m+1=1，
解得：m=0．
20. 【分析】先列表把函数的对应点的坐标表示出来，再根据表中点的坐标在平面直角坐标系中描出对应的点，最后连线就可以得出函数的图象．
解：
列表为：
x … -2 -1 -0.5 0.5 1 2 …
y= … -0.5 -1 -2 2 1 0.5 …
描点并连线为：
21.【分析】 （1）将点（m，2）代入y=2x-1可求出m的值，然后再代入y=可求出k的值．
（2）将（1）求得的两个解析式联立解方程可得出另外一个交点．
解：（1）把（m，2）代入y=2x-1，得2=2m-1，∴m= ）
把（，2）代入，得2=
∴k=3；
（2）由（1）知，y=2x-1
∴=2x-1
∴x1=，x2=-1
∴y1=2，y2=-3
∴两图象的另一交点坐标为（-1，-3）．
22. 【分析】（1）根据反比例函数的性质可知：在这个函数图象的每一支上，y随x增大而增大，则k-2＜0，解不等式即可得到答案；
（2）首先把P（-1，a）代入函数关系式y=-2x+4中，可以求出a的值，从而得到P点坐标，再把P点坐标代入反比例函数中，即可求出k的值，从而可得到反比例函数的解析式．
解：（1）∵在这个函数图象的每一支上，y随x增大而增大，
∴k-2＜0，
k＜2；
（2）∵P（-1，a）在函数y=-2x+4的图象上，
∴a=-2×（-1）+4=6，
∴P（-1，6），
∵P又在反比例函数图象上，
∴k-2=-1×6，
k=-4，
∴反比例函数的解析式为：y=．
23. 【分析】由一次函数x=2与反比例函数y=和y=-的图象分别交于A、B两点，可求得点A与B的坐标，即可求得边AB的长，又由P是y轴上任意一点，可求得P到直线AB的距离为2，继而求得△PAB的面积．
解：连接PA，PB，
∵一次函数x=2与反比例函数y=和y=-的图象分别交于A、B两点，
∴点A的坐标为：（2，1），点B的坐标为：（2，-），
∴AB=1-（-）=，
∵P是y轴上任意一点，
∴P到直线AB的距离为2，
∴S△PAB=××2=．
24. 【分析】根据反比例函数系数k的几何意义可得|k|=3，再计算出k的值，再根据所在象限确定出k，然后表示出反比例函数解析式，再把A点坐标代入反比例函数解析式，进而计算选出m的值．
解：∵S△AOB=3，
∴|k|=3，
k=±6，
∵函数图象在第二象限，
∴k=-6，
∴反比例函数解析式为y=-，
∵反比例函数y=-的图象过点A（-2，m），
∴-2m=-6，
解得：m=3．
25. 【分析】（1）根据和谐点的定义，把利用点M、N的坐标分别求得矩形OAMB、OANB的周长与面积进行验证即可；
（2）根据和谐点的定义和反比例函数系数k的几何意义列出关于方程，通过解方程可以求得a、b的值．
解：（1）点M不是和谐点，点N是和谐点．
理由：∵M（l，2），
∴L=（1+2）×2=6，S=1×2=2，
∵L≠S，
∴M（l，2）不是和谐点；
∵N（4，4），
∴L=（4+4）×2=16，S=4×4=16，
∵L=S，
∴N（4，4）是和谐点；
（2）∵P（a，3）是和谐点，
∴（a+3）×2=3a，
解得a=6．
∴P（6，3）代入y=，
得：b=6×3=18．
综上所述，a=6，b=18．
26. （1）首先根据题意可知药物燃烧阶段，室内每立方米空气中的含药量y与燃烧时间x成正比例，故设函数关系式为y=k1x（k1≠0），再利用待定系数法把（10，8）代入即可求出函数关系式；
（2）燃烧后y与x成反比例；且其图象都过点（10，8），将数据代入用待定系数法可得反比例函数的关系式；
（3）根据题意得：，在解不等式组即可得答案．
（1）设药物燃烧阶段函数解析式为y=k1x（k1≠0），
由题意得：8=10k1，
解得：k1=，
故此阶段函数解析式为y=x（0≤x≤10）；
（2）设药物燃烧结束后函数解析式为y=（k2≠0），
由题意得：，
解得：k2=80，
故此阶段函数解析式为（x≥10）；
（3）由题意得：，
解得：2≤x≤50，
50-2=48（分钟），
故本次消毒的有效时长为48分钟．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)