九年级数学上册 22.3 实际问题与二次函数(第3课时拱桥问题)课件
文档属性
| 名称 | 九年级数学上册 22.3 实际问题与二次函数(第3课时拱桥问题)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 161.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-10 00:00:00 | ||
图片预览




文档简介
课件12张PPT。实际问题与二次函数第三课时拱桥问题广东省怀集县冷坑镇观塘初级中学 韩文丽1、若正方形的周长为 a cm,面积为 S cm2,则S与a的函数关系为( )
S=a2 B. C. D
2、二次函数y=x2+2x-5取最小值时,自变量x的值是 ;
3、已知二次函数y=x2-6x+m的最小值为1,那么m的值是 。cX=-1m=101、会建立直角坐标系解决实际问题;
2、会解决与桥洞水面宽度有关的类似问题。学习目标引入新课广东省怀集县冷坑镇观塘中学 韩文丽利用二次函数解决抛物线建筑物问题 探究 3 图中是抛物线拱桥,当拱顶离水面2m时,水面宽4m,水面下降1m,水面宽度增加多少?分析:二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数,为解题简便,怎样建立平面直角坐标系才合适呢?(如下图)
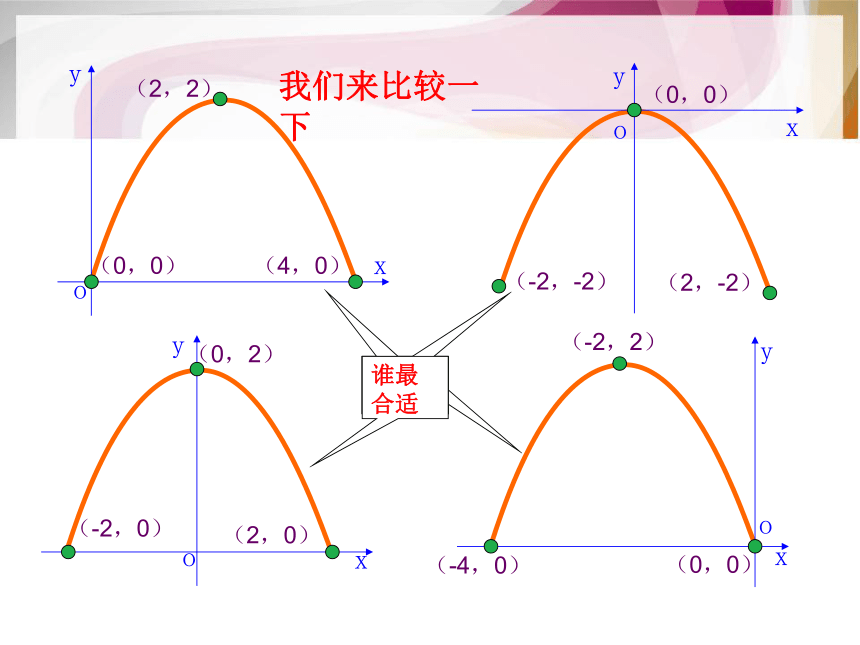
我们来比较一下(0,0)(4,0)(2,2)(-2,-2)(2,-2)(0,0)(-2,0)(2,0)(0,2)(-4,0)(0,0)(-2,2)谁最合适yyyyooooxxxx设这条抛物线表示的二次函数为
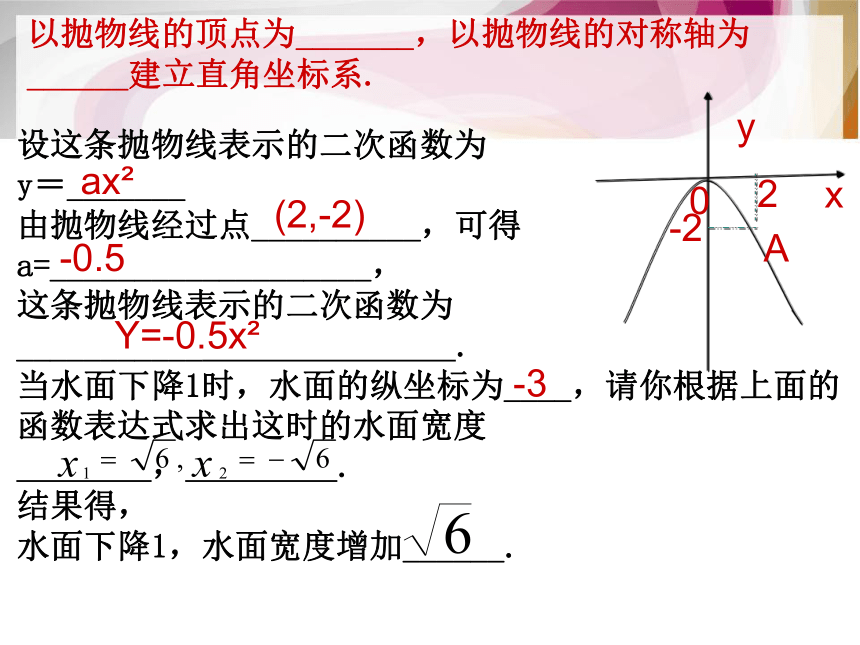
y=_______
由抛物线经过点__________,可得
a=___________________,
这条抛物线表示的二次函数为
___________ .
当水面下降1时,水面的纵坐标为____,请你根据上面的函数表达式求出这时的水面宽度
, .
结果得,
水面下降1,水面宽度增加______.以抛物线的顶点为_______,以抛物线的对称轴为______建立直角坐标系.广东省怀集县冷坑镇观塘中学 韩文丽温馨提示:解此类问题的思想方法是利用数形结合思想和函数思想,合理建立直角坐标系,根据已知数据,运用 _________法求出运动轨迹(即抛物线)的解析式,再用二次函数的性质去分析解决问题.待定系数法练一练1、如图所示,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
A、x>3
B、x<3
C、x>1
D、x<1c2、某工厂的大门是一抛物线形水泥建筑物,如图,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?解:如图,以AB所在的直线为X轴,以AB的垂直平分线为Y轴,建立平面直角坐标系
∵AB=4 ∴A(-2,0) B(2,0)
∵OC=4.4 ∴C(0,4.4)
设抛物线所表示的二次函数为y=ax2+4.4
∵抛物线过A(-2,0)
∴4a+4.4=0 ∴a=-1.1
∴抛物线所表示的二次函数为 y=1.1x2+4.4
当x=1.2时,y=-1.1×1.22+4.4=2.816>2.8 ∴汽车能顺利经过大门 3、如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米. AO= 3米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1) 直接写出点A及抛物线顶点P的坐标;
(2) 求出这条抛物线的函数解析式;广东省怀集县冷坑镇观塘中学 韩文丽解:⑴ A(0,3) P(6,6) (2)设抛物线的函数解析式为y=ax2+bx+c,函数图像经过A(0,3),B(12,3),P(6,6)则
解得1、用二次函数解决抛物线形建筑问题都可以构建二次函数解析式,解此类问题的思想方法是利用 和 思想,合理建立直角坐标系,根据已知数据,运用 求出运动轨迹(即抛物线)的解析式,再用二次的性质去分析解决问题。四、归纳小结数形结合函数待定系数法
S=a2 B. C. D
2、二次函数y=x2+2x-5取最小值时,自变量x的值是 ;
3、已知二次函数y=x2-6x+m的最小值为1,那么m的值是 。cX=-1m=101、会建立直角坐标系解决实际问题;
2、会解决与桥洞水面宽度有关的类似问题。学习目标引入新课广东省怀集县冷坑镇观塘中学 韩文丽利用二次函数解决抛物线建筑物问题 探究 3 图中是抛物线拱桥,当拱顶离水面2m时,水面宽4m,水面下降1m,水面宽度增加多少?分析:二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数,为解题简便,怎样建立平面直角坐标系才合适呢?(如下图)
我们来比较一下(0,0)(4,0)(2,2)(-2,-2)(2,-2)(0,0)(-2,0)(2,0)(0,2)(-4,0)(0,0)(-2,2)谁最合适yyyyooooxxxx设这条抛物线表示的二次函数为
y=_______
由抛物线经过点__________,可得
a=___________________,
这条抛物线表示的二次函数为
___________ .
当水面下降1时,水面的纵坐标为____,请你根据上面的函数表达式求出这时的水面宽度
, .
结果得,
水面下降1,水面宽度增加______.以抛物线的顶点为_______,以抛物线的对称轴为______建立直角坐标系.广东省怀集县冷坑镇观塘中学 韩文丽温馨提示:解此类问题的思想方法是利用数形结合思想和函数思想,合理建立直角坐标系,根据已知数据,运用 _________法求出运动轨迹(即抛物线)的解析式,再用二次函数的性质去分析解决问题.待定系数法练一练1、如图所示,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
A、x>3
B、x<3
C、x>1
D、x<1c2、某工厂的大门是一抛物线形水泥建筑物,如图,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?解:如图,以AB所在的直线为X轴,以AB的垂直平分线为Y轴,建立平面直角坐标系
∵AB=4 ∴A(-2,0) B(2,0)
∵OC=4.4 ∴C(0,4.4)
设抛物线所表示的二次函数为y=ax2+4.4
∵抛物线过A(-2,0)
∴4a+4.4=0 ∴a=-1.1
∴抛物线所表示的二次函数为 y=1.1x2+4.4
当x=1.2时,y=-1.1×1.22+4.4=2.816>2.8 ∴汽车能顺利经过大门 3、如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米. AO= 3米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1) 直接写出点A及抛物线顶点P的坐标;
(2) 求出这条抛物线的函数解析式;广东省怀集县冷坑镇观塘中学 韩文丽解:⑴ A(0,3) P(6,6) (2)设抛物线的函数解析式为y=ax2+bx+c,函数图像经过A(0,3),B(12,3),P(6,6)则
解得1、用二次函数解决抛物线形建筑问题都可以构建二次函数解析式,解此类问题的思想方法是利用 和 思想,合理建立直角坐标系,根据已知数据,运用 求出运动轨迹(即抛物线)的解析式,再用二次的性质去分析解决问题。四、归纳小结数形结合函数待定系数法
同课章节目录
