第2章 三角形单元过关检测A卷

21世纪教育网 –中小学教育资源及组卷应用平台
三角形单元过关检测A卷
考号_______ 姓名___________总分________
一、选择题（共12题；共48分）
1.如图所示，小敏做试题时 ( http: / / www.21cnjy.com )，不小心把题目中的三角形用墨水弄污了一部分，她想在一块白纸上作一个完全一样的三角形，然后粘贴在上面，她作图的依据是（ ） 21*cnjy*com
( http: / / www.21cnjy.com / )
A、SSS B、SAS C、ASA D、AAS21cnjy.com
2.用尺规作图，下列条件中可能作出两个不同的三角形的是（ ）
A、已知三边 B、已知两角及夹边 C、已知两边及夹角 D、已知两边及其中一边的对角
3.已知等腰三角形的一个内角是70°，则这个等腰三角形的顶角为（ ）
A、70° B、40° C、70°或40° D、以上答案都不对
4.如图，在△ABC中，∠B，∠C的平分线BE，CD相交于点F，∠ABC=42°，∠A=60°，则∠BFC=（ ） ( http: / / www.21cnjy.com / )21·cn·jy·com
A、118° B、119° C、120° D、121°www.21-cn-jy.com
5.一个等腰三角形的两边长分别为4，8，则它的周长为（ ）
A、12 B、16 C、20 D、16或2021·世纪*教育网
6.下列判断两个三角形全等的条件中，正确的是（ ）
A、一条边对应相等 B、两条边对应相等 C、三个角对应相等 D、三条边对应相等
7. G是△ABC的重心，连接AG并延长交边BC于D，若△ABC的面积为6cm2，则△BGD的面积为（ ）
A．2cm2 B．3cm2 C．1cm2 D． ( http: / / www.21cnjy.com / )cm221教育网
8.在等腰△ABC中，AB=AC，其周长为16cm，则AB边的取值范围是（　　）
A、1cm＜AB＜4cm B、3cm＜AB＜6cm C、4cm＜AB＜8cm D、5cm＜AB＜10cm
9.如图，已知AB=AC， BD=CD， 那么下列结论中不正确的是（ ）
( http: / / www.21cnjy.com / )
A、△ABD≌△ACD B、∠ADB=90° C、∠BAD是∠B的一半 D、AD平分∠BAC
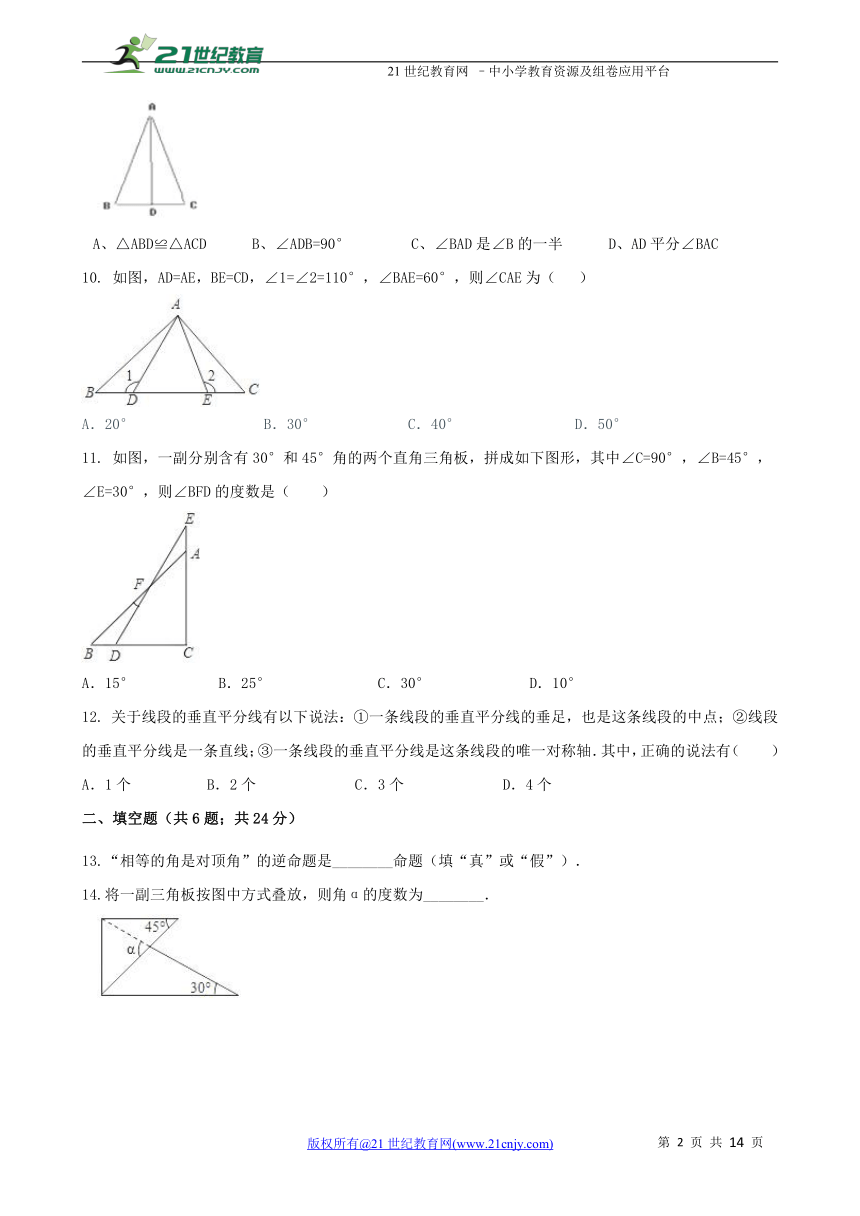
10. 如图，AD=AE，BE=CD，∠1=∠2=110°，∠BAE=60°，则∠CAE为（ ）
( http: / / www.21cnjy.com / )
A．20° B．30° C．40° D．50°
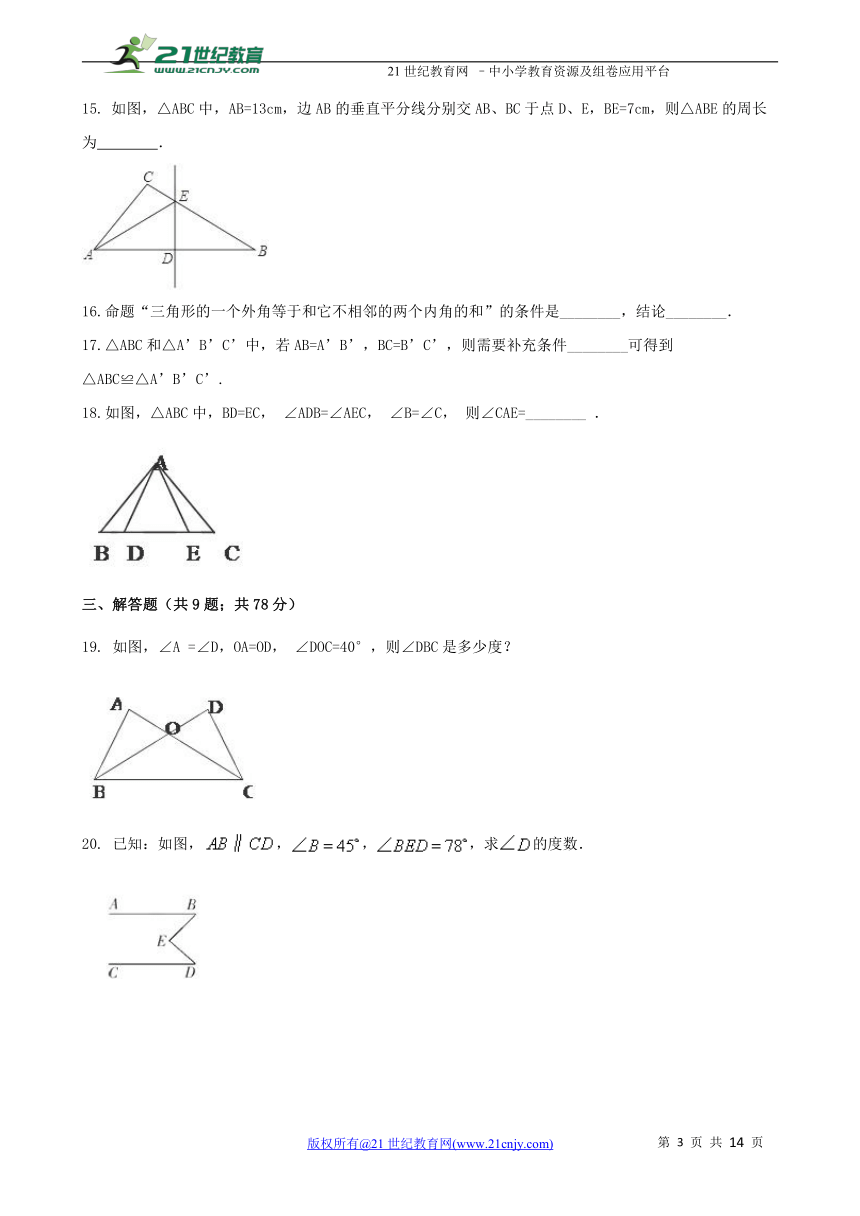
11. 如图，一副分别含有30°和45°角 ( http: / / www.21cnjy.com )的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（　　）2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A．15° B．25° C．30° D．10°【来源：21·世纪·教育·网】
12. 关于线段的垂直平分线有以下说法： ( http: / / www.21cnjy.com )①一条线段的垂直平分线的垂足，也是这条线段的中点；②线段的垂直平分线是一条直线；③一条线段的垂直平分线是这条线段的唯一对称轴．其中，正确的说法有（ ）
A．1个 B．2个 C．3个 D．4个【来源：21cnj*y.co*m】
二、填空题（共6题；共24分）
13.“相等的角是对顶角”的逆命题是________命题（填“真”或“假”）．
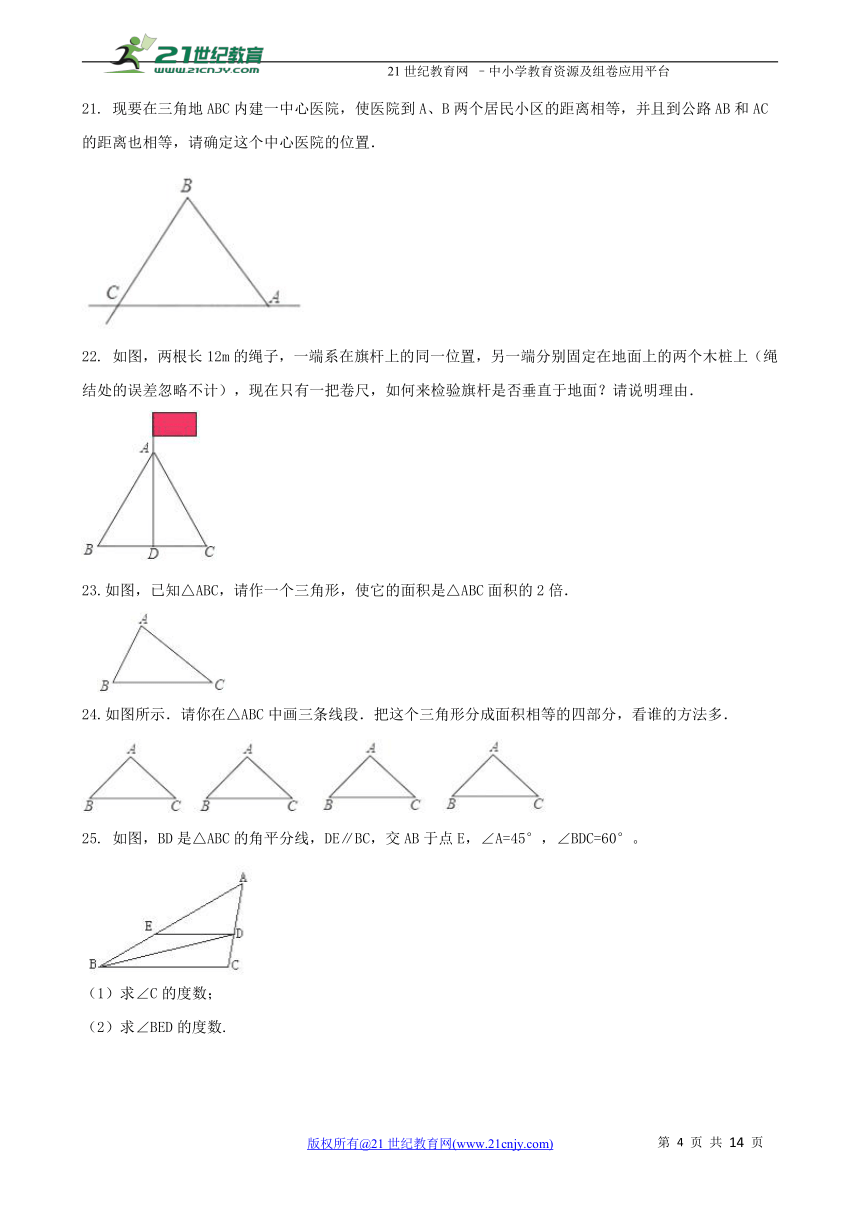
14.将一副三角板按图中方式叠放，则角α的度数为________．
( http: / / www.21cnjy.com / )
15. 如图，△ABC中，AB=13cm，边AB的垂直平分线分别交AB、BC于点D、E，BE=7cm，则△ABE的周长为 ．
( http: / / www.21cnjy.com / ) 【出处：21教育名师】
16.命题“三角形的一个外角等于和它不相邻的两个内角的和”的条件是________，结论________．
17.△ABC和△A’B’C’中，若AB=A’B’，BC=B’C’，则需要补充条件________可得到△ABC≌△A’B’C’.
18.如图，△ABC中，BD=EC， ∠ADB=∠AEC， ∠B=∠C， 则∠CAE=________ ．
( http: / / www.21cnjy.com / )
三、解答题（共9题；共78分）
19. 如图，∠A =∠D，OA=OD， ∠DOC=40°，则∠DBC是多少度？
( http: / / www.21cnjy.com / )
20. 已知：如图， ( http: / / www.21cnjy.com / )， ( http: / / www.21cnjy.com / )， ( http: / / www.21cnjy.com / )，求 ( http: / / www.21cnjy.com / )的度数．
( http: / / www.21cnjy.com / )
21. 现要在三角地ABC内建一中心医院，使医院到A、B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置．
( http: / / www.21cnjy.com / )21教育名师原创作品
22. 如图，两根长12m ( http: / / www.21cnjy.com )的绳子，一端系在旗杆上的同一位置，另一端分别固定在地面上的两个木桩上（绳结处的误差忽略不计），现在只有一把卷尺，如何来检验旗杆是否垂直于地面？请说明理由．
( http: / / www.21cnjy.com / )
23.如图，已知△ABC，请作一个三角形，使它的面积是△ABC面积的2倍．
( http: / / www.21cnjy.com / )
24.如图所示．请你在△ABC中画三条线段．把这个三角形分成面积相等的四部分，看谁的方法多． ( http: / / www.21cnjy.com / )
25. 如图，BD是△ABC的角平分线，DE∥BC，交AB于点E，∠A=45°，∠BDC=60°。
( http: / / www.21cnjy.com / )
（1）求∠C的度数；
（2）求∠BED的度数.
26. 已知：点D是等边△ABC边上任意一点，∠ABD=∠ACE，BD=CE．
（1）说明△ABD≌△ACE的理由；
（2）△ADE是什么三角形？为什么？
( http: / / www.21cnjy.com / ) www-2-1-cnjy-com
27.如图，已知BE⊥AD，CF⊥AD，且BE=CF．
（1）请你判断AD是否为△ABC的中线；
（2）当AB与AC满足什么条件时，AD是△ABC的角平分线？请分析说明理由．
( http: / / www.21cnjy.com / )
【版权所有：21教育】
答案解析
一、选择题
1、【分析】图中的三角形已知一条边以及两个角，利用全等三角形的判定（ASA）可作图．
解：图中的三角形已知一条边以及两个角，则她作图的依据是ASA．
故选C．
2、【分析】看是否符合所学的全等的公理或定理即可．
解：A、B、C分别符合全等三角形的判定 ( http: / / www.21cnjy.com )SSS、ASA、SAS，故能作出唯一三角形；D、可能作出两个不同的三角形，如等腰三角形底边上的任一点与顶点之间的线段两侧的三角形；
故选D．
3、【分析】首先要进行分析题意，“等腰三角形的一个内角”没明确是顶角还是底角，所以要分两种情况进行讨论．
解：本题可分两种情况： ①当70 ( http: / / www.21cnjy.com )°角为底角时，顶角为180°﹣2×70°=40°；
②70°角为等腰三角形的顶角；
因此这个等腰三角形的顶角为40°或70°．
故选C．
4、【分析】由三角形内角和定理得∠ ( http: / / www.21cnjy.com )ABC+∠ACB=120°，由角平分线的性质得∠CBE+∠BCD=60°，再利用三角形的内角和定理得结果．
解：∵∠A=60°， ∴∠ABC+∠ACB=120°，
∵BE，CD是∠B、∠C的平分线，
∴∠CBE= ( http: / / www.21cnjy.com / )∠ABC，∠BCD= ( http: / / www.21cnjy.com / )，
∴∠CBE+∠BCD= ( http: / / www.21cnjy.com / )（∠ABC+∠BCA）=60°，
∴∠BFC=180°﹣60°=120°，
故选：C．
5、【分析】由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析．
解：①当4为腰时，4+4=8，故此种情况不存 ( http: / / www.21cnjy.com )在；
②当8为腰时，8﹣4＜8＜8+4，符合题意．
故此三角形的周长=8+8+4=20．
故选C．
6、【分析】考查学生对三角形全等的判定方法的掌握情况．此处可以运用排除法进行分析．
解：判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
故只有D符合SSS能判定三角形全等．
故选D．
7、【分析】根据三角形的重心的性质和等底等高的三角形的面积相等来计算．
解：由题意得， ( http: / / www.21cnjy.com / )=1cm2．
故选C．
8、【分析】设AB=AC= ( http: / / www.21cnjy.com )x，则BC=16﹣2x，根据三角形的三边关系：两边之和大于第三边，两边之差小于第三边列不等式组，即可得出结论．
解：∵在等腰△ABC中，AB=AC，其周长为16cm，
∴设AB=AC=x cm，则BC=（16﹣2x）cm，
( http: / / www.21cnjy.com / )
解得4cm＜x＜8cm．
故选：C．
9、【分析】因为已知AB ( http: / / www.21cnjy.com )=DC ， BD=CD ， AD=AD ， 则可得△ABD≌△ACD；∠ADB=90°；∠BAD=∠CAD即AD平分∠BAC.
解：因为已知AB=DC ， BD=CD ， AD=AD（公共边），则A项成立；B项成立； D项成立；只有C项不成立；
10、【分析】运用SAS证明△ABD≌△ACE，得∠B=∠C．根据三角形内角和定理可求∠DAE的度数．则易求∠CAE的度数．
【解析】
如图，∵∠1=∠2=110°，
∴∠ADE=∠AED=70°，
∴∠DAE=180°-2°．
∵BE=CD，∴BD=CE．
在△ABD和△ACE中，
( http: / / www.21cnjy.com / )，
∴△ABD≌△ACE（SAS）
∴∠BAD=∠CAE．
∵∠BAE=60°，
∴∠BAD=∠CAE=20°．
故选A．
11、【分析】 先由三角形外角的性质求出∠BDF的度数，根据三角形内角和定理即可得出结论．
解：∵Rt△CDE中，∠C=90°，∠E=30°，
∴∠BDF=∠C+∠E=90°+30°=120°，
∵△BDF中，∠B=45°，∠BDF=120°，
∴∠BFD=180°﹣45°﹣120°=15°．
故选A．
12、【分析】由线段垂直平分线的定义， ( http: / / www.21cnjy.com )可得一条线段的垂直平分线的垂足，也是这条线段的中点；线段的垂直平分线是一条直线．注意举反例的解题方法．
解：①一条线段的垂直平分线的垂足，也是这条线段的中点，正确；
②线段的垂直平分线是一条直线；正确；
③一条线段的垂直平分线是这条线段的唯一对称轴．错误，线段有2条对称轴：还有本身．
故选B．
二、填空题
13、解：“相等的角是对顶角”的条件是 ( http: / / www.21cnjy.com )：两个角相等，结论是：这两个角是对顶角，
所以逆命题是：如果两个角是对顶角，那么这 两个角相等，是真命题.
故答案为：真.
14、【分析】先根据直角三角板的性质求出∠1及∠2的度数，再根据三角形内角与外角的关系即可解答．
解：∵图中是一副三角板， ∴∠2=45°，∠1=90°﹣45°=45°，
∴∠α=∠1+30°=45°+30°=75°．
故答案为：75°．
( http: / / www.21cnjy.com / )
15、【分析】根据线段垂直平分线上 ( http: / / www.21cnjy.com )的点到线段两端点的距离相等可得AE=BE，然后根据三角形的周长公式列式计算即可得解．
解：∵DE是AB的垂直平分线，
∴AE=BE=7cm，
∴△ABE的周长=AB+AE+BE=13+7+7=27cm．
故答案为：27cm．
16、【分析】解答本题的关键是要掌握“如果”后面的是条件，“那么”后面的是结论。
解：先把命题写成“如果”，“那么”的形式 ( http: / / www.21cnjy.com )，“如果”后面的是条件，“那么”后面的是结论。
命题“三角形的一个外角等于和它不相邻的两个内角的和”的条件是一个角是三角形的外角，结论是等于和它不相邻的两个内角的和．
17、【分析】本题考查了三角形全等的相关知识。
解：可以补充AC=A’C’，理由：SSS（边边边）；或者补充角∠ABC=∠A’B’C’，理由：SAS（边角边）。
18、【分析】根据ASA可判定两三角形全等，再根据全等三角形的对应角相等，可完成此题．
解：∵∠ADB=∠AEC ， BD=EC ， ∠B=∠C∴△ABD≌△ACE( ASA), ∠CAE=∠BAD.
三、解答题
19、【分析】结合图形和所给条件可判定两三角形全等，再根据全等三角形的性质得出对应角对应相等，利用等腰三角形的性质和外角就可解得此题．2-1-c-n-j-y
解：∵∠A =∠D ， OA=OD ， ∠AOB =∠DOC,
∴△AOB≌△DOC(ASA),OB=OC ，
∴△BOC是等腰三角形，∠DBC =∠ACB,
∵∠DOC=40°
∴∠DBC=1/2∠DOC=20°．
20、【分析】 延长BE交CD于点F ( http: / / www.21cnjy.com )得到∠1，根据两直线平行，内错角相等的性质得到∠1=∠B，再根据三角形的一个外角等于和它不相邻的两个内角的和即可求出∠D的度数．
解：如图，延长BE交CD于点F，
( http: / / www.21cnjy.com / )
∵AB∥CD，∠B=45°，
∴∠1=∠B=45°，
∴∠D=∠BED-∠1=78°-45°=33°．
21、【分析】根据线段垂直平分线性质作出AB的垂直平分线，根据角平分线性质作出∠BAC的角平分线，即可得出答案．21世纪教育网版权所有
解：
( http: / / www.21cnjy.com / )
作AB的垂直平分线EF，作∠BAC的角平分线AM，两线交于P，
则P为这个中心医院的位置．

22、【分析】用卷尺测量出BD=CD，然后利用“SSS”证明△ABD和△ACD全等，根据全等三角形对应角相等可得∠ADB=∠ADC，再求出∠ADB=∠ADC=90°，即可进行判定．
解：用卷尺测量出BD、CD，看它们是否相等，若BD=CD，则AD⊥BC．
理由如下：∵在△ABD和△ACD中，
( http: / / www.21cnjy.com / )，
∴△ABD≌△ACD（SSS），
∴∠ADB=∠ADC，
又∵∠ADB+∠ADC=180°，
∴∠ADB=∠ADC=90°，
即AD⊥BC．
23、【分析】延长BC到D，使CD=BC，然后根据等高的三角形的面积的比等于底边的比即可得解．
解：如图，延长BC到D，使CD=BC， 则BD=2BC，
设点A到BC的距离为h，
则S△ABD= ( http: / / www.21cnjy.com / )BD h= ( http: / / www.21cnjy.com / ) 2BC h=2 ( http: / / www.21cnjy.com / ) BC h=2S△ABC ，
所以，△ABD即为所求作的三角形．
( http: / / www.21cnjy.com / )
24、【分析】方法一：取各边中点顺次连 ( http: / / www.21cnjy.com )接，依据三角形中位线定理可得所得符合条件； 方法二：将一边四等分，把分点与这边相对的顶点连接，根据等底同高的三角形的面积相等可得符合条件．
方法三：可先作出三角形的中位线把三角形的面积二等分，进而再利用三角形的中线把三角形的面积分成相等的2部分，把所得的2个三角形继续二等分即可．
解： ( http: / / www.21cnjy.com / )
①如图1，可取各边的中点顺次连接；
②如图2，把BC四等分，让BC的四等分点分别与A连接．
③如图3，先把△ABC分成面积相等的两部分，进而再做分得两个三角形的中线即可把△ABC分成面积相等的四部分．
④分别取BC、AB、AC的中点，的中点D、E、F，连接AD、CE、EF
25、【分析】（1）∠C的度数 ( http: / / www.21cnjy.com )=180°-∠A-∠ABC，因此应先求出∠ABC的度数；根据三角形的外角的性质可得，∠ABD=∠BDC-∠A=60°-45°=15°．再根据角平分线的定义可得，∠ABC=2∠ABD=2×15°=30°，从而可求∠C的度数
（2）求∠BED的度数，根据两直线平行，同旁内角互补得∠BED的度数．
解：（1）∵∠BDC是△ABD的外角，
∴∠ABD=∠BDC-∠A=60°-45°=15°．
∵BD是△ABC的角平分线，
∴∠DBC=15°
∴∠ABC=2∠DBC=30°
∴∠C=180°-∠A-∠ABC=180°-45°-30°=105°；
（2）∵DE∥BC，
∴∠BDE=15°．
∴∠BED=180°-∠BDE-∠DBE=180°-15°-15°=150°．
26、【分析】（1）根据全等三角形的判 ( http: / / www.21cnjy.com )定定理SAS证得△ABD≌△ACE；
（2）利用（1）中的全等三角形的对应边相等判定AD=AE，则△ADE是等腰三角形．
证明：（1）如图，∵△ABC是等边三角形，
∴AB=AC．
在△ABD与△ACE中，
( http: / / www.21cnjy.com / )，
∴△ABD≌△ACE（SAS）；
解：（2）△ADE是等腰三角形．理由如下：
∵由（1）知△ABD≌△ACE，
∴AD=AE，∴△ADE是等腰三角形．21*cnjy*com
27、【分析】（1）求出∠BED=∠CFD，根据AAS证出△BED≌△CFD即可；
（2）根据等腰三角形的性质三线合一定理求出即可．
解：（1）∵BE⊥AD，CF⊥AD，
∴∠CFD=∠BED=90°，
在△BED和△CFD中
( http: / / www.21cnjy.com / )
∴△BED≌△CFD（AAS），
∴BD=DC，
即AD是△ABC的中线．
（2）当AB=AC时，AD为△ABC的角平分线，
理由是：∵AB=AC，AD为△ABC的中线，
∴AD为△ABC的角平分线．
( http: / / www.21cnjy.com / )
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)