2017-2018学年人教A版必修五 正弦定理和余弦定理 习题课 课件(31张)
文档属性
| 名称 | 2017-2018学年人教A版必修五 正弦定理和余弦定理 习题课 课件(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 00:00:00 | ||
图片预览











文档简介
课件31张PPT。第一章 解三角形习题课 正弦定理和余弦定理1.学会利用三角形中的隐含条件.
2.进一步熟练掌握正弦、余弦定理在解各类三角形中的应用.
3.初步应用正弦、余弦定理解决一些和三角函数、向量有关的综合问题.学习目标题型探究问题导学内容索引当堂训练问题导学思考 知识点一 有关三角形的隐含条件我们知道y=sin x在区间(0,π)上不单调,所以由0<α<β<π得不到sin α<sin β.那么由A,B为△ABC的内角且A<B,能得到sin A<sin B吗?为什么?答案能.由于三角形中大边对大角,
∴当A<B时,有a<b.
由正弦定理,得2Rsin A<2Rsin B,
从而有sin A<sin B.“三角形”这一条件隐含着丰富的信息,利用这些信息可以得到富有三角形特色的变形和结论:
(1)由A+B+C=180°可得
sin(A+B)= ,cos(A+B)= ,
tan(A+B)= ,
=______.梳理sin C-cos C-tan C(2)由三角形的几何性质可得
acos C+ccos A= ,bcos C+ccos B= ,
acos B+bcos A= .
(3)由大边对大角可得sin A>sin B?A B.
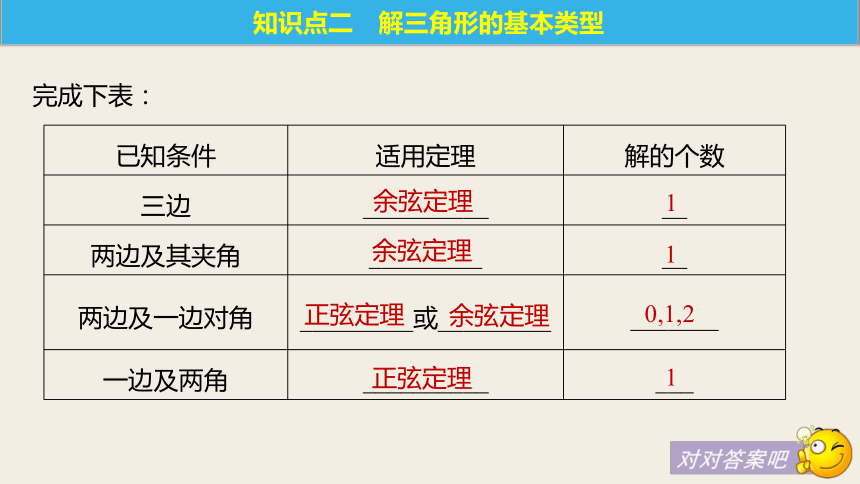
(4)由锐角△ABC可得sin A cos B.bac>>知识点二 解三角形的基本类型完成下表:余弦定理1余弦定理1正弦定理余弦定理0,1,2正弦定理1这类问题通常要借助正弦定理或余弦定理进行边角互化,转化为代数问题或者三角恒等式,再利用三角恒等变换解决问题,中间往往会用到一些三角形的隐含条件如内角和等.知识点三 三角形有关问题的解决思路题型探究例1 在△ABC中,若c·cos B=b·cos C, 求sin B的值.类型一 利用正弦、余弦定理解三角形解答
由c·cos B=b·cos C,结合正弦定理,得
sin Ccos B=sin Bcos C,
故sin(B-C)=0,∵0∴-π1.对于例1中的条件,c·cos B=b·cos C,能否使用余弦定理?解答
化简得a2+c2-b2=a2+b2-c2,
∴c2=b2,从而c=b.2.例1中的条件c·cos B=b·cos C的几何意义是什么?解答
如图,
作AD⊥BC,垂足为D.
则c·cos B=BD,b·cos C=CD.
∴ccos B=bcos C的几何意义为边AB,
AC在BC边上的射影相等.(1)边、角互化是处理三角形边、角混合关系的常用手段;
(2)解题时要画出三角形,将题目条件直观化,根据题目条件,灵活选择公式.跟踪训练1 在△ABC中,已知b2=ac,a2-c2=ac-bc.
(1)求A的大小;解答
由题意知,
解答(1)求A的度数;类型二 正弦、余弦定理与三角变换的综合应用解答
4(1+cos A)-4cos2 A=5,
即4cos2A-4cos A+1=0,∵0°化简并整理,得(b+c)2-a2=3bc,解答(1)解三角形的实质是解方程,利用正弦、余弦定理,通过边、角互化,建立未知量的代数方程或三角方程.
(2)三角形内角和定理在判断角的范围、转化三角函数、检验所求角是否符合题意等问题中有着重要的作用.
解答类型三 正弦、余弦定理与平面向量的综合应用解答
∴ac=35,又∵a=7,∴c=5.由余弦定理,得b2=a2+c2-2accos B=32,∵c∵m∥n,150°又0°∴B=150°.答案解析当堂训练√123答案解析
在△ABC中,利用正弦定理,得123答案解析
1233.已知△ABC中,a=x,b=2,B=45°,若这个三角形有两解,则x的取值范围是 .
若三角形有两解,必须满足CD<22.解决正弦定理与余弦定理的综合应用问题,应注意根据具体情况引入未知数,运用方程思想来解决问题;平面向量与解三角形的交汇问题,应注意准确运用向量知识转化为解三角形问题,再利用正弦、余弦定理求解. 本课结束
2.进一步熟练掌握正弦、余弦定理在解各类三角形中的应用.
3.初步应用正弦、余弦定理解决一些和三角函数、向量有关的综合问题.学习目标题型探究问题导学内容索引当堂训练问题导学思考 知识点一 有关三角形的隐含条件我们知道y=sin x在区间(0,π)上不单调,所以由0<α<β<π得不到sin α<sin β.那么由A,B为△ABC的内角且A<B,能得到sin A<sin B吗?为什么?答案能.由于三角形中大边对大角,
∴当A<B时,有a<b.
由正弦定理,得2Rsin A<2Rsin B,
从而有sin A<sin B.“三角形”这一条件隐含着丰富的信息,利用这些信息可以得到富有三角形特色的变形和结论:
(1)由A+B+C=180°可得
sin(A+B)= ,cos(A+B)= ,
tan(A+B)= ,
=______.梳理sin C-cos C-tan C(2)由三角形的几何性质可得
acos C+ccos A= ,bcos C+ccos B= ,
acos B+bcos A= .
(3)由大边对大角可得sin A>sin B?A B.
(4)由锐角△ABC可得sin A cos B.bac>>知识点二 解三角形的基本类型完成下表:余弦定理1余弦定理1正弦定理余弦定理0,1,2正弦定理1这类问题通常要借助正弦定理或余弦定理进行边角互化,转化为代数问题或者三角恒等式,再利用三角恒等变换解决问题,中间往往会用到一些三角形的隐含条件如内角和等.知识点三 三角形有关问题的解决思路题型探究例1 在△ABC中,若c·cos B=b·cos C, 求sin B的值.类型一 利用正弦、余弦定理解三角形解答
由c·cos B=b·cos C,结合正弦定理,得
sin Ccos B=sin Bcos C,
故sin(B-C)=0,∵0
化简得a2+c2-b2=a2+b2-c2,
∴c2=b2,从而c=b.2.例1中的条件c·cos B=b·cos C的几何意义是什么?解答
如图,
作AD⊥BC,垂足为D.
则c·cos B=BD,b·cos C=CD.
∴ccos B=bcos C的几何意义为边AB,
AC在BC边上的射影相等.(1)边、角互化是处理三角形边、角混合关系的常用手段;
(2)解题时要画出三角形,将题目条件直观化,根据题目条件,灵活选择公式.跟踪训练1 在△ABC中,已知b2=ac,a2-c2=ac-bc.
(1)求A的大小;解答
由题意知,
解答(1)求A的度数;类型二 正弦、余弦定理与三角变换的综合应用解答
4(1+cos A)-4cos2 A=5,
即4cos2A-4cos A+1=0,∵0°
(2)三角形内角和定理在判断角的范围、转化三角函数、检验所求角是否符合题意等问题中有着重要的作用.
解答类型三 正弦、余弦定理与平面向量的综合应用解答
∴ac=35,又∵a=7,∴c=5.由余弦定理,得b2=a2+c2-2accos B=32,∵c
在△ABC中,利用正弦定理,得123答案解析
1233.已知△ABC中,a=x,b=2,B=45°,若这个三角形有两解,则x的取值范围是 .
若三角形有两解,必须满足CD<2
