2017-2018学年人教A版必修五 3.2一元二次不等式及其解法(一) 课件(35张)
文档属性
| 名称 | 2017-2018学年人教A版必修五 3.2一元二次不等式及其解法(一) 课件(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 00:00:00 | ||
图片预览










文档简介
课件35张PPT。第三章 不等式§3.2 一元二次不等式及其解法(一)1.理解一元二次方程、一元二次不等式与二次函数的关系.
2.掌握图象法解一元二次不等式.
3.体会数形结合、分类讨论思想.学习目标题型探究问题导学内容索引当堂训练问题导学思考 知识点一 一元二次不等式的概念不等式x2>1的解集为{x|x<-1或x>1},该集合中每一个元素都是不等式的解,而不等式的每一个解均属于解集.答案我们知道,方程x2=1的解集是{1,-1},解集中的每一个元素均可使等式成立.那么你能写出不等式x2>1的解集吗?梳理 (1)只含有一个未知数,并且未知数的最高次数是2的不等式,称为 不等式.
(2)能使不等式成立的未知数x的一个值称为不等式的一个解.
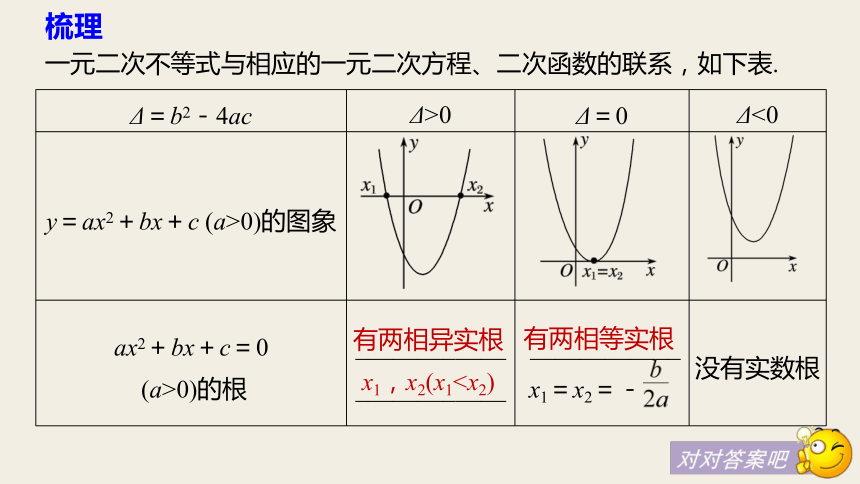
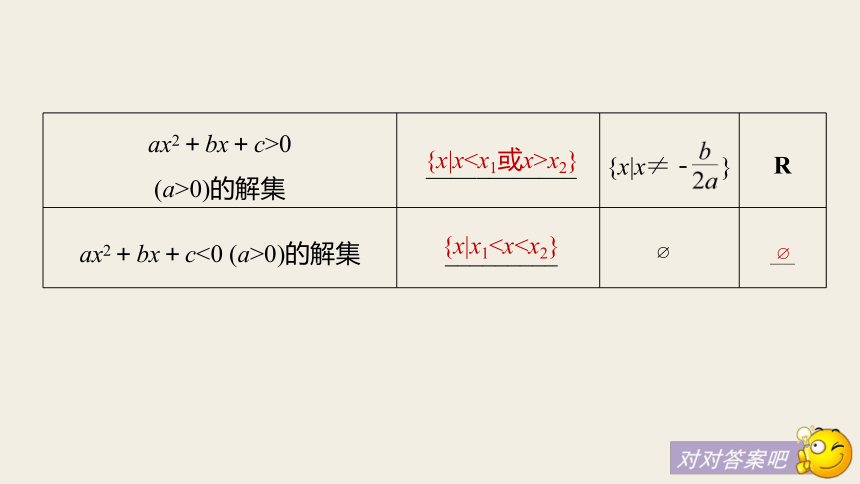
(3)不等式所有解的 称为解集.一元二次集合知识点二 “三个二次”的关系思考 分析二次函数y=x2-1与一元二次方程x2-1=0和一元二次不等式x2-1>0之间的关系.答案梳理 一元二次不等式与相应的一元二次方程、二次函数的联系,如下表.有两相异实根
x1,x2(x1x2}{x|x10.
∵方程x2-3x+2=0的根x1=1,x2=2,
∴原不等式的解集为{x|x<1或x>2}.答案根据上表,尝试解不等式x2+2>3x.梳理 解一元二次不等式的步骤:
(1)化为基本形式ax2+bx+c>0或ax2+bx+c<0(其中a>0);
(2)计算Δ=b2-4ac,以确定一元二次方程ax2+bx+c=0是否有解;
(3)有根求根;
(4)根据图象写出不等式的解集.题型探究类型一 一元二次不等式的解法命题角度1 二次项系数大于0
例1 求不等式4x2-4x+1>0的解集.解答因为Δ=(-4)2-4×4×1=0,
所以方程4x2-4x+1=0的解是x1=x2= ,
所以原不等式的解集为 .
当所给不等式是非一般形式的不等式时,应先化为一般形式,在具体求解一个一般形式的一元二次不等式的过程中,要密切结合一元二次方程的根的情况以及二次函数的图象.跟踪训练1 求不等式2x2-3x-2≥0的解集.∵2x2-3x-2=0的两解为x1=- ,x2=2,
且a=2>0,
∴不等式2x2-3x-2≥0的解集是{x|x≤- 或x≥2}.解答命题角度2 二次项系数小于0
例2 解不等式-x2+2x-3>0.不等式可化为x2-2x+3<0.
因为Δ<0,方程x2-2x+3=0无实数解,
而y=x2-2x+3的图象开口向上,
所以原不等式的解集是?.解答将-x2+2x-3>0转化为x2-2x+3<0的过程注意符号的变化,这是解本题关键之处.跟踪训练2 求不等式-3x2+6x>2的解集.不等式可化为3x2-6x+2<0,
∵Δ=(-6)2-4×3×2=12>0,
解答∴不等式-3x2+6x>2的解集是命题角度3 含参数的二次不等式
例3 解关于x的不等式ax2-(a+1)x+1<0.解答当a<0时,不等式可化为(x- )(x-1)>0,
∵a<0,∴ <1,
∴不等式的解集为{x|x< 或x>1}.
当a=0时,不等式即-x+1<0,解集为{x|x>1}.
当a>0时,不等式可化为(x- )(x-1)<0.
当0<a<1时, >1,不等式的解集为{x|1<x< }.
当a=1时,不等式的解集为?.
当a>1时,<1,不等式的解集为{x| <x<1}.综上,当a<0时,解集为{x|x< 或x>1};
当a=0时,解集为{x|x>1};
当0<a<1时,解集为{x|1<x< };
当a=1时,解集为?;
当a>1时,解集为{x| <x<1}.解含参数的不等式,可以按常规思路进行:先考虑开口方向,再考虑判别式的正负,最后考虑两根的大小关系,当遇到不确定因素时再讨论.跟踪训练3 解关于x的不等式(x-a)(x-a2)<0.解答当a<0或a>1时,
有a<a2,此时,不等式的解集为{x|a<x<a2};
当0<a<1时,
有a2<a,此时,不等式的解集为{x|a2<x<a};
当a=0或a=1时,原不等式无解.
综上,当a<0或a>1时,原不等式的解集为{x|a<x<a2};
当0<a<1时,原不等式的解集为{x|a2<x<a};
当a=0或a=1时,解集为?.类型二 “三个二次”间对应关系的应用例4 已知关于x的不等式x2+ax+b<0的解集为{x|1<x<2},试求关于x的不等式bx2+ax+1>0的解集.由根与系数的关系,可得
∴不等式bx2+ax+1>0,即2x2-3x+1>0.
由2x2-3x+1>0,解得x< 或x>1.
∴bx2+ax+1>0的解集为 .解答给出一元二次不等式的解集,相当于知道了相应二次函数的开口方向及与x轴的交点,可以利用代入根或根与系数的关系求待定系数.跟踪训练4 已知不等式ax2-bx+2<0的解集为{x|10,且1,2是方程ax2-bx+2=0的两实根.
由根与系数的关系,知
方法二 把x=1,2分别代入方程ax2-bx+2=0中,
得当堂训练1.不等式2x2-x-1>0的解集是答案解析123√45∵2x2-x-1=(2x+1)(x-1),
∴由2x2-x-1>0,得(2x+1)(x-1)>0,
解得x>1或x<- ,
∴不等式的解集为 .
2.不等式-6x2-x+2≤0的解集是√答案解析12345∵-6x2-x+2≤0,
∴6x2+x-2≥0,
∴(2x-1)(3x+2)≥0,
∴x≥ 或x≤- .3.若不等式ax2+8ax+21<0的解集是{x|-7A.1 B.2 C.3 D.4√答案解析12345由题意可知-7和-1为方程ax2+8ax+21=0的两个根.
∴-7×(-1)= ,故a=3.4.不等式x2+x-2<0的解集为__________.答案解析由x2+x-2<0,得-2故其解集为{x|-2所以a=2时解集为R.
当a-2≠0时,由题意得
12345解答解得-2综上所述,a的取值范围为(-2,2].1.解一元二次不等式的常见方法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m0,则可得x>n或x若(x-m)(x-n)<0,则可得m有口诀如下:大于取两边,小于取中间.
2.含参数的一元二次型的不等式
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,讨论需从如下三个方面进行考虑:
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:两根(Δ>0),一根(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,x1=x2,x1
2.掌握图象法解一元二次不等式.
3.体会数形结合、分类讨论思想.学习目标题型探究问题导学内容索引当堂训练问题导学思考 知识点一 一元二次不等式的概念不等式x2>1的解集为{x|x<-1或x>1},该集合中每一个元素都是不等式的解,而不等式的每一个解均属于解集.答案我们知道,方程x2=1的解集是{1,-1},解集中的每一个元素均可使等式成立.那么你能写出不等式x2>1的解集吗?梳理 (1)只含有一个未知数,并且未知数的最高次数是2的不等式,称为 不等式.
(2)能使不等式成立的未知数x的一个值称为不等式的一个解.
(3)不等式所有解的 称为解集.一元二次集合知识点二 “三个二次”的关系思考 分析二次函数y=x2-1与一元二次方程x2-1=0和一元二次不等式x2-1>0之间的关系.答案梳理 一元二次不等式与相应的一元二次方程、二次函数的联系,如下表.有两相异实根
x1,x2(x1
∵方程x2-3x+2=0的根x1=1,x2=2,
∴原不等式的解集为{x|x<1或x>2}.答案根据上表,尝试解不等式x2+2>3x.梳理 解一元二次不等式的步骤:
(1)化为基本形式ax2+bx+c>0或ax2+bx+c<0(其中a>0);
(2)计算Δ=b2-4ac,以确定一元二次方程ax2+bx+c=0是否有解;
(3)有根求根;
(4)根据图象写出不等式的解集.题型探究类型一 一元二次不等式的解法命题角度1 二次项系数大于0
例1 求不等式4x2-4x+1>0的解集.解答因为Δ=(-4)2-4×4×1=0,
所以方程4x2-4x+1=0的解是x1=x2= ,
所以原不等式的解集为 .
当所给不等式是非一般形式的不等式时,应先化为一般形式,在具体求解一个一般形式的一元二次不等式的过程中,要密切结合一元二次方程的根的情况以及二次函数的图象.跟踪训练1 求不等式2x2-3x-2≥0的解集.∵2x2-3x-2=0的两解为x1=- ,x2=2,
且a=2>0,
∴不等式2x2-3x-2≥0的解集是{x|x≤- 或x≥2}.解答命题角度2 二次项系数小于0
例2 解不等式-x2+2x-3>0.不等式可化为x2-2x+3<0.
因为Δ<0,方程x2-2x+3=0无实数解,
而y=x2-2x+3的图象开口向上,
所以原不等式的解集是?.解答将-x2+2x-3>0转化为x2-2x+3<0的过程注意符号的变化,这是解本题关键之处.跟踪训练2 求不等式-3x2+6x>2的解集.不等式可化为3x2-6x+2<0,
∵Δ=(-6)2-4×3×2=12>0,
解答∴不等式-3x2+6x>2的解集是命题角度3 含参数的二次不等式
例3 解关于x的不等式ax2-(a+1)x+1<0.解答当a<0时,不等式可化为(x- )(x-1)>0,
∵a<0,∴ <1,
∴不等式的解集为{x|x< 或x>1}.
当a=0时,不等式即-x+1<0,解集为{x|x>1}.
当a>0时,不等式可化为(x- )(x-1)<0.
当0<a<1时, >1,不等式的解集为{x|1<x< }.
当a=1时,不等式的解集为?.
当a>1时,<1,不等式的解集为{x| <x<1}.综上,当a<0时,解集为{x|x< 或x>1};
当a=0时,解集为{x|x>1};
当0<a<1时,解集为{x|1<x< };
当a=1时,解集为?;
当a>1时,解集为{x| <x<1}.解含参数的不等式,可以按常规思路进行:先考虑开口方向,再考虑判别式的正负,最后考虑两根的大小关系,当遇到不确定因素时再讨论.跟踪训练3 解关于x的不等式(x-a)(x-a2)<0.解答当a<0或a>1时,
有a<a2,此时,不等式的解集为{x|a<x<a2};
当0<a<1时,
有a2<a,此时,不等式的解集为{x|a2<x<a};
当a=0或a=1时,原不等式无解.
综上,当a<0或a>1时,原不等式的解集为{x|a<x<a2};
当0<a<1时,原不等式的解集为{x|a2<x<a};
当a=0或a=1时,解集为?.类型二 “三个二次”间对应关系的应用例4 已知关于x的不等式x2+ax+b<0的解集为{x|1<x<2},试求关于x的不等式bx2+ax+1>0的解集.由根与系数的关系,可得
∴不等式bx2+ax+1>0,即2x2-3x+1>0.
由2x2-3x+1>0,解得x< 或x>1.
∴bx2+ax+1>0的解集为 .解答给出一元二次不等式的解集,相当于知道了相应二次函数的开口方向及与x轴的交点,可以利用代入根或根与系数的关系求待定系数.跟踪训练4 已知不等式ax2-bx+2<0的解集为{x|1
由根与系数的关系,知
方法二 把x=1,2分别代入方程ax2-bx+2=0中,
得当堂训练1.不等式2x2-x-1>0的解集是答案解析123√45∵2x2-x-1=(2x+1)(x-1),
∴由2x2-x-1>0,得(2x+1)(x-1)>0,
解得x>1或x<- ,
∴不等式的解集为 .
2.不等式-6x2-x+2≤0的解集是√答案解析12345∵-6x2-x+2≤0,
∴6x2+x-2≥0,
∴(2x-1)(3x+2)≥0,
∴x≥ 或x≤- .3.若不等式ax2+8ax+21<0的解集是{x|-7
∴-7×(-1)= ,故a=3.4.不等式x2+x-2<0的解集为__________.答案解析由x2+x-2<0,得-2
当a-2≠0时,由题意得
12345解答解得-2
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m
2.含参数的一元二次型的不等式
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,讨论需从如下三个方面进行考虑:
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:两根(Δ>0),一根(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,x1=x2,x1
