2017-2018学年人教A版必修5 基本不等式 课件(15张)
文档属性
| 名称 | 2017-2018学年人教A版必修5 基本不等式 课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 00:00:00 | ||
图片预览






文档简介
课件14张PPT。目标:
1.能熟练应均值不等式证明不等式;
2.掌握利用重要不等式求最值的方法
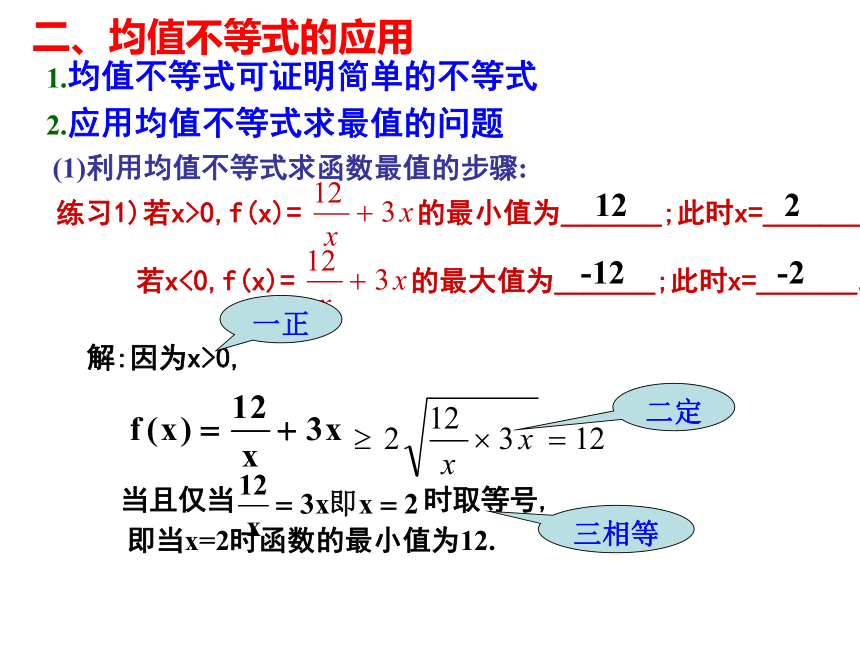
均值不等式的应用 一、复习:①a,b∈R,a2 +b2≥2ab1. 基本不等式,均值不等式:2.上面两个重要不等式有如下变形及推广:②a,b是正数, (当且仅当a=b时取”=“号)(当且仅当a=b时取“=”号)当a1,a2, … ,an是正数时 (当且仅当a=b=c时取“=”号)二、均值不等式的应用1.均值不等式可证明简单的不等式例1. 1)已知:a,b,c均为正数,求证:证明:所以,原不等式成立当且仅当a=b=c时,取等号.二、均值不等式的应用1.均值不等式可证明简单的不等式例1. 1)已知:a,b,c均为正数,求证:2)已知:正数a,b,c满足a+b+c=1,求证:3)a>0,b>0且a+b=1,求证:二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题如课本作业5,6:一正,二定,三相等③必须有自变量值能使函数取到 = 号.①各项必须为正;②含变数的各项和或积必须为定值;(1)利用均值不等式求函数最值的步骤:二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:练习1)若x>0,f(x)= 的最小值为_______;此时x=_______.解:因为x>0, 若x<0,f(x)= 的最大值为_______;此时x=_______.即当x=2时函数的最小值为12.122-12-2当且仅当 时取等号,一正二定三相等二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:练习1)若x>0,f(x)= 的最小值为_______;此时x=_______. 若x<0,f(x)= 的最大值为_______;此时x=_______.122-12-2错解!注意:各项必须为正数正解:当且仅当 时取“=”号例2. 函数y= (x ≥ 0)的最小值为______,此时x=______.解:≥2-1=1当且仅当 时取“=”号练习 :1.求函数 的最小值.即当 时,函数的最小值为解:012.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:(2)先变形再利用均值不等式求函数最值:2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:(2)先变形再利用均值不等式求函数最值:练习2:求函数 的最大值,
并求出相应x的值.(3)取不到等号时用函数单调性求最值:例3.求函数 的最小值.当且仅当 时取等号错解:2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:(2)先变形再利用均值不等式求函数最值:(3)取不到等号时用函数单调性求最值:例3.求函数 的最小值.利用函数 (t>0)的单调性.单调递减单调递增依据:正解:例4已知 a、b为常数,且 求证:x+y的最小值为小结:二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:一正,二定,三相等(2)先变形再利用均值不等式求函数最值:(3)取不到等号时用函数单调性求最值:随堂练习下课,谢谢!
1.能熟练应均值不等式证明不等式;
2.掌握利用重要不等式求最值的方法
均值不等式的应用 一、复习:①a,b∈R,a2 +b2≥2ab1. 基本不等式,均值不等式:2.上面两个重要不等式有如下变形及推广:②a,b是正数, (当且仅当a=b时取”=“号)(当且仅当a=b时取“=”号)当a1,a2, … ,an是正数时 (当且仅当a=b=c时取“=”号)二、均值不等式的应用1.均值不等式可证明简单的不等式例1. 1)已知:a,b,c均为正数,求证:证明:所以,原不等式成立当且仅当a=b=c时,取等号.二、均值不等式的应用1.均值不等式可证明简单的不等式例1. 1)已知:a,b,c均为正数,求证:2)已知:正数a,b,c满足a+b+c=1,求证:3)a>0,b>0且a+b=1,求证:二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题如课本作业5,6:一正,二定,三相等③必须有自变量值能使函数取到 = 号.①各项必须为正;②含变数的各项和或积必须为定值;(1)利用均值不等式求函数最值的步骤:二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:练习1)若x>0,f(x)= 的最小值为_______;此时x=_______.解:因为x>0, 若x<0,f(x)= 的最大值为_______;此时x=_______.即当x=2时函数的最小值为12.122-12-2当且仅当 时取等号,一正二定三相等二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:练习1)若x>0,f(x)= 的最小值为_______;此时x=_______. 若x<0,f(x)= 的最大值为_______;此时x=_______.122-12-2错解!注意:各项必须为正数正解:当且仅当 时取“=”号例2. 函数y= (x ≥ 0)的最小值为______,此时x=______.解:≥2-1=1当且仅当 时取“=”号练习 :1.求函数 的最小值.即当 时,函数的最小值为解:012.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:(2)先变形再利用均值不等式求函数最值:2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:(2)先变形再利用均值不等式求函数最值:练习2:求函数 的最大值,
并求出相应x的值.(3)取不到等号时用函数单调性求最值:例3.求函数 的最小值.当且仅当 时取等号错解:2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:(2)先变形再利用均值不等式求函数最值:(3)取不到等号时用函数单调性求最值:例3.求函数 的最小值.利用函数 (t>0)的单调性.单调递减单调递增依据:正解:例4已知 a、b为常数,且 求证:x+y的最小值为小结:二、均值不等式的应用1.均值不等式可证明简单的不等式2.应用均值不等式求最值的问题(1)利用均值不等式求函数最值的步骤:一正,二定,三相等(2)先变形再利用均值不等式求函数最值:(3)取不到等号时用函数单调性求最值:随堂练习下课,谢谢!
