2017秋高二数学人教A版必修5 应用举例 课件(31张)
文档属性
| 名称 | 2017秋高二数学人教A版必修5 应用举例 课件(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 09:31:42 | ||
图片预览






文档简介
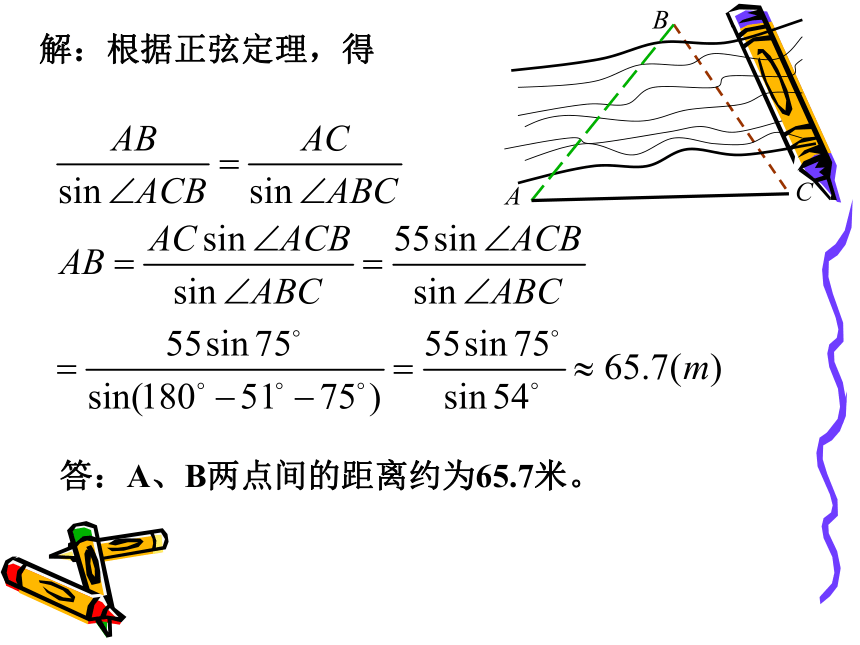
课件31张PPT。正弦定理余弦定理举例应用问题1. A、B两点在河的两岸(B点不可到达),要测量
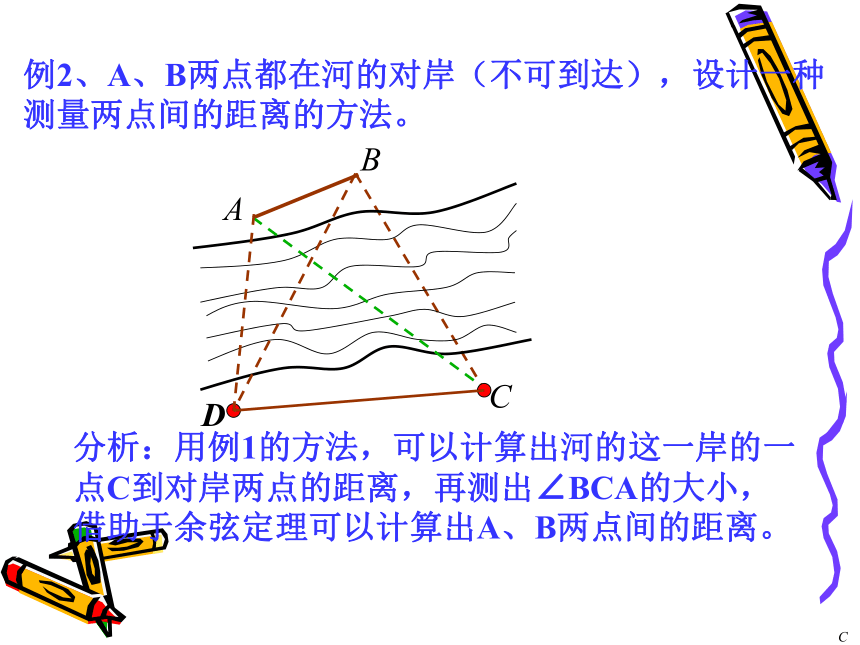
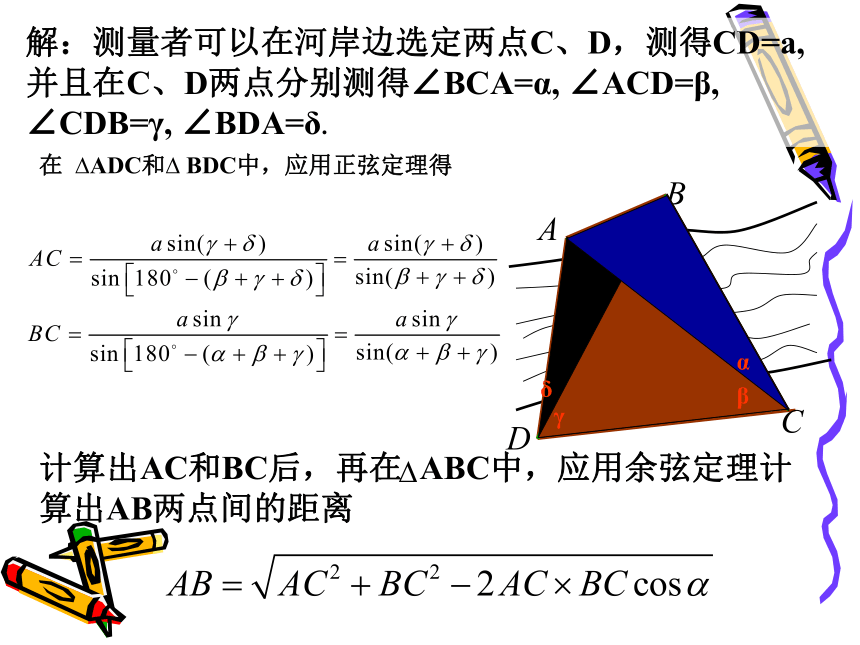
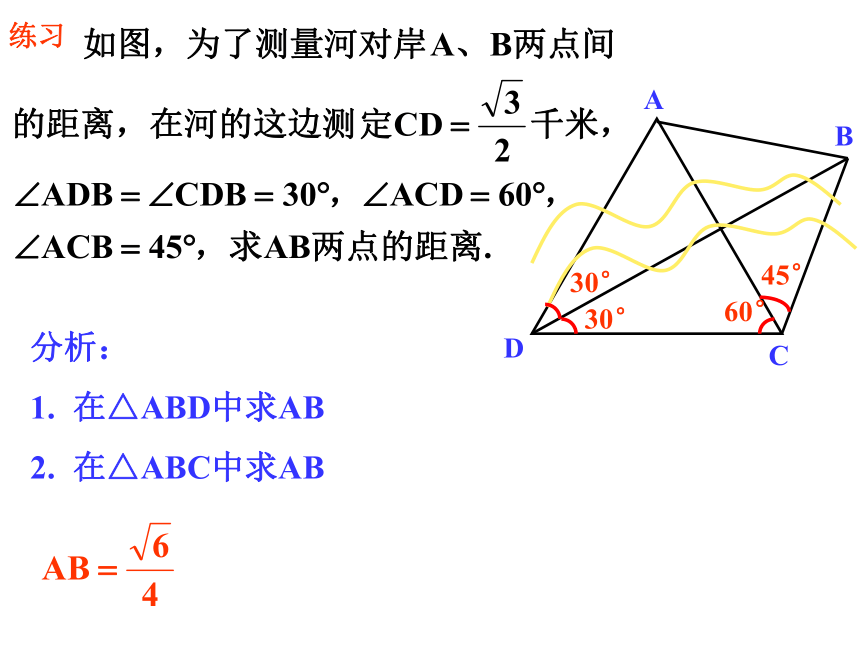
这两点之间的距离。(备用工具:皮尺、测角仪)测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m).分析:所求的边AB的对角是已知的,又知三角形的一边AC,根据三角形内角和定理可计算出边AC的对角,根据正弦定理,可以计算出边AB.你能根据所学知识设计一种测量方案吗?解:根据正弦定理,得答:A、B两点间的距离约为65.7米。例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。D解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在 ?ADC和? BDC中,应用正弦定理得βγδαABCD30°45°30°60°分析:
在△ABD中求AB
在△ABC中求AB练习1、分析题意,弄清已知和所求;
2、根据题意,画出示意图;
3、将实际问题转化为数学问题,写出已知所求;
4、正确运用正、余弦定理解三角形。
5、检验并作答。小结:求解三角形应用题的一般步骤:练习:教材P14 1,2如何测量地球与月亮之间的距离?背景资料早在1671年,两位法国天文学家为了测量地球与月球之间的距离,利用几乎位于同一子午线的柏林与好望角,测量计算出α,β的大小和两地之间的距离,从而算出了地球与月球之间的距离约为385400km. 解决有关三角形应用性问题的思路、
步骤和方法实际问题 抽象概括
画示意图 建立数学模型推理 演算数学模型的解实际问题
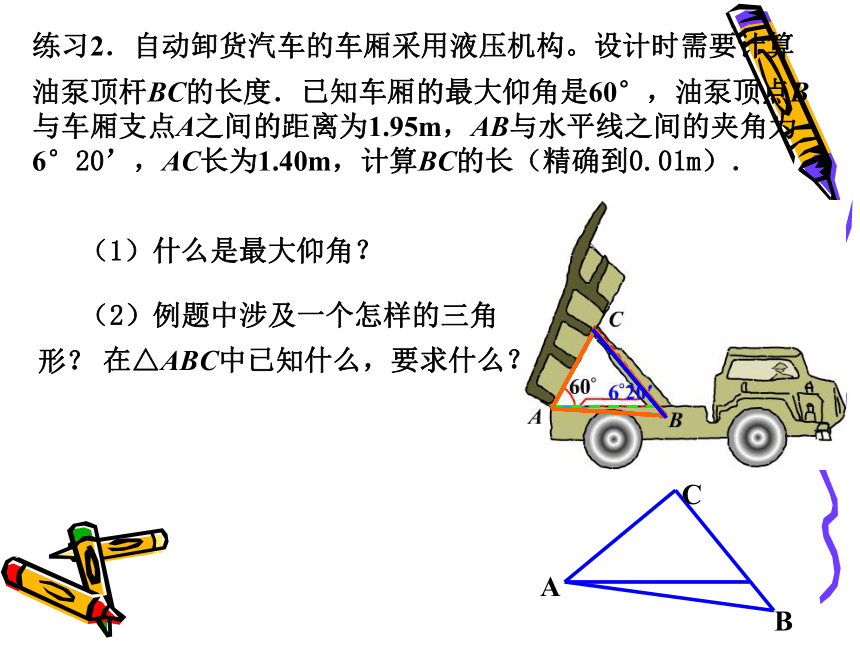
的 解检验作答还原说明课堂小结:通过本节课,你有什么收获?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). (1)什么是最大仰角? 在△ABC中已知什么,要求什么?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
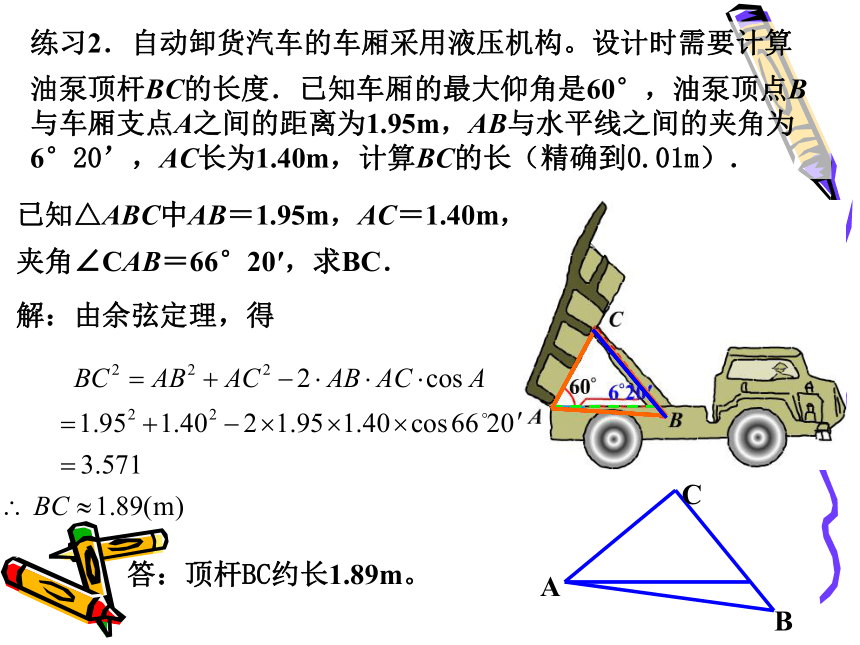
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.解:由余弦定理,得答:顶杆BC约长1.89m。 有关测量术语:
a.仰角和俯角是指与目标视线在同一垂直平
面内的水平视线的夹角.其中目标视线在水平
视线的目标视线上方时叫仰角,目标视线在水
平视线的下方的时叫俯角.
b.方向角是指从指定方向线到目标方向线的
水平角,如北偏东300,南偏西450.
c.方位角是指从正北方向是顺时针旋转到目
标方向线的角.
d.坡度是坡面与水平面所成的角的度数.问题二:测量高度问题(1):底部不可以到达问题二:测量高度问题(2):底部可以到达例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。问题三:测量角度问题答:此船应该沿北偏东560的方向航行,需要航行113.15 n mile.3. 3.5m长的木棒斜靠在石堤旁,棒的一端离堤足1.2m的地面上,另一端沿堤上2.8m的地方,求地对地面的倾斜角。四、面积公式推导△应用四:有关三角形计算 例8: 如图,在某市进行城市环境建设中,要把一个三角形的区域改造成市内公园,经过测量得到这个三角形区域的三条边分别为68m, 88m, 127m, 这个区域的面积是多少?(精确到0.1m2)应用四:有关三角形计算 解:设a=68m , b=88m, c=127m, 根据余弦定理可得:答:这个区域的面积是2840.4m2应用五:三角形恒等式证明应用五:三角形恒等式证明1、审题(分析题意,弄清已知和所求,根据提意,画出示意图;
2.建模(将实际问题转化为解斜三角形的数学问题)
3.求模(正确运用正、余弦定理求解)
4,还原。小结:求解三角形应用题的一般步骤:
这两点之间的距离。(备用工具:皮尺、测角仪)测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m).分析:所求的边AB的对角是已知的,又知三角形的一边AC,根据三角形内角和定理可计算出边AC的对角,根据正弦定理,可以计算出边AB.你能根据所学知识设计一种测量方案吗?解:根据正弦定理,得答:A、B两点间的距离约为65.7米。例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。D解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在 ?ADC和? BDC中,应用正弦定理得βγδαABCD30°45°30°60°分析:
在△ABD中求AB
在△ABC中求AB练习1、分析题意,弄清已知和所求;
2、根据题意,画出示意图;
3、将实际问题转化为数学问题,写出已知所求;
4、正确运用正、余弦定理解三角形。
5、检验并作答。小结:求解三角形应用题的一般步骤:练习:教材P14 1,2如何测量地球与月亮之间的距离?背景资料早在1671年,两位法国天文学家为了测量地球与月球之间的距离,利用几乎位于同一子午线的柏林与好望角,测量计算出α,β的大小和两地之间的距离,从而算出了地球与月球之间的距离约为385400km. 解决有关三角形应用性问题的思路、
步骤和方法实际问题 抽象概括
画示意图 建立数学模型推理 演算数学模型的解实际问题
的 解检验作答还原说明课堂小结:通过本节课,你有什么收获?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). (1)什么是最大仰角? 在△ABC中已知什么,要求什么?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.解:由余弦定理,得答:顶杆BC约长1.89m。 有关测量术语:
a.仰角和俯角是指与目标视线在同一垂直平
面内的水平视线的夹角.其中目标视线在水平
视线的目标视线上方时叫仰角,目标视线在水
平视线的下方的时叫俯角.
b.方向角是指从指定方向线到目标方向线的
水平角,如北偏东300,南偏西450.
c.方位角是指从正北方向是顺时针旋转到目
标方向线的角.
d.坡度是坡面与水平面所成的角的度数.问题二:测量高度问题(1):底部不可以到达问题二:测量高度问题(2):底部可以到达例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。问题三:测量角度问题答:此船应该沿北偏东560的方向航行,需要航行113.15 n mile.3. 3.5m长的木棒斜靠在石堤旁,棒的一端离堤足1.2m的地面上,另一端沿堤上2.8m的地方,求地对地面的倾斜角。四、面积公式推导△应用四:有关三角形计算 例8: 如图,在某市进行城市环境建设中,要把一个三角形的区域改造成市内公园,经过测量得到这个三角形区域的三条边分别为68m, 88m, 127m, 这个区域的面积是多少?(精确到0.1m2)应用四:有关三角形计算 解:设a=68m , b=88m, c=127m, 根据余弦定理可得:答:这个区域的面积是2840.4m2应用五:三角形恒等式证明应用五:三角形恒等式证明1、审题(分析题意,弄清已知和所求,根据提意,画出示意图;
2.建模(将实际问题转化为解斜三角形的数学问题)
3.求模(正确运用正、余弦定理求解)
4,还原。小结:求解三角形应用题的一般步骤:
