2017-2018学年人教A版必修5 等比数列 课件(22张)
文档属性
| 名称 | 2017-2018学年人教A版必修5 等比数列 课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 521.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 09:22:03 | ||
图片预览








文档简介
课件22张PPT。2.4 等比数列学习目标:1.理解等比数列的定义;
2.掌握等比数列的通项公式.会解决知道n, 中的三个,求另一个的问题.
学习重点:
1.等比数列概念的理解与掌握;
2.等比数列的通项公式的推导及应用.
课题导入课本P48页的4个例子:(1)细胞分裂问题(2)“一尺之棰,日取其半,万世不竭”(3)计算机病毒感染问题(4)银行复利计算问题①1,2,4,8,16,…②1,,,,,…③1,20,,,,…④,,,,……请同学们仔细观察一下,看看以上①、②、③、④
四个数列有什么共同特征?从第二项起,每一项与它前一项之比等于同一常数.探究一:等比数列的定义(1)1,2,22,23,…观察下列数列,说出它们的特点.定义:如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,记为q(q≠0).数学语言:探究一:等比数列的定义(判断一个数列是否为等比数列的依据)
1.已知等比数列{ an }:
(1) an 能不能是零?
(2)公比q能不能是1?
2.用下列方法表示的数列中能确定
是等比数列的是 .
① 1,-1,1,…,(-1)n+1 ; ②1,2,4,6…;
③a,a,a,…,a; ④已知a1=2,an=3an+1 ;
⑤
⑥2a,2a,2a,…,2a.
3.什么样的数列既是等差数列又是等比数列?不能能√√√×××非零的
常数列① ④ ⑥思考1:思考2:
若a,G,b三个数成等比数列,那么这 三个数有何恒等关系?结论:G2=abG叫做a,b的等比中项通项公式 数学式
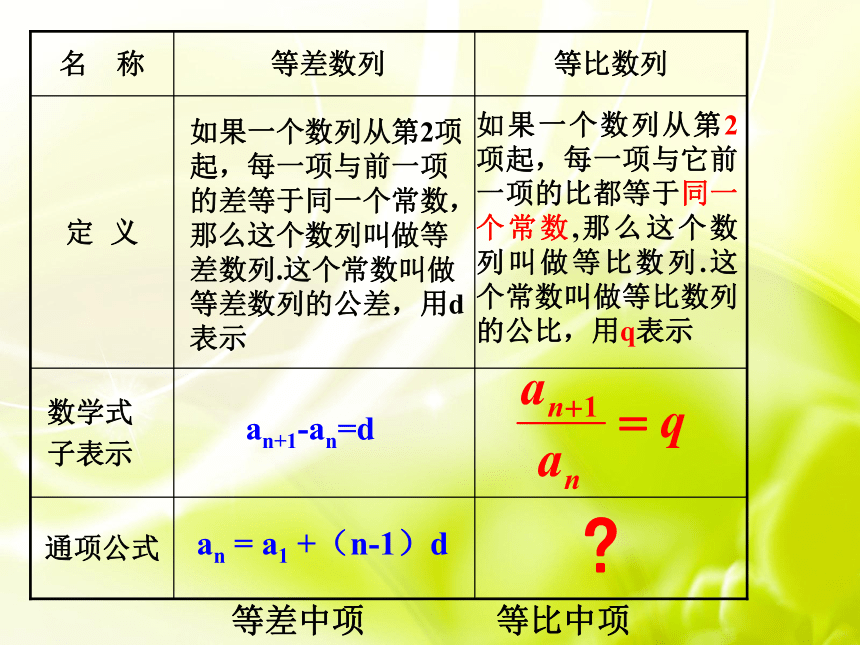
子表示定 义等比数列 等差数列名 称如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列.这个常数叫做等差数列的公差,用d表示an+1-an=dan = a1 +(n-1)d如果一个数列从第2项起,每一项与它前一项的比都等于同一个常数,那么这个数列叫做等比数列.这个常数叫做等比数列的公比,用q表示?等差中项等比中项探究二:通项公式思考3:如何用a1和q表示第n项an
a2/a1=q
a3/a2=q
a4/a3=q
…
an/an-1=q其中,a1与q均不为0。由于当n=1时上面等式两边均为a1,
即等式也成立,说明上面公式当n∈N*时都成立,因此它
就是等比数列{an}的通项公式。这n-1个式子相乘得an/a1=qn-1
所以 an=a1qn-1
1.叠乘法(累乘法)
a2=a1q
a3=a2q=a1q2
a4=a3q=a1q3
…
an=a1qn-12.不完全归纳法a1q2a1q3a1qn-1等比数列的通项公式:
(n∈N﹡,q≠0)例如:数列{an}的首项是a1=1,公比q=2,则通项公式是: ______上式还可以写成可见,这个等比数列
的图象都在函数
的图象上,如右图所示。 0 1 2 3 4 nan
8
7
6
5
4
3
2
1····思考4:等比数列的通项公式与函数有怎样的关系?世界杂交水稻之父—袁隆平从1976年至1999年在我国累计推广种植杂交水稻35亿多亩,增产稻谷3500亿公斤。年增稻谷可养活6000万人口。 西方世界称他的杂交稻是“东方魔稻” ,并认为是解决下个世纪世界性饥饿问题的法宝。接轨生活 袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?由于每代的种子数是它的前一代种子数的120倍,因此,逐代的种子数组成等比数列,记为 答:到第5代大约可以得到这种新品种的种子2.5×1010粒.解:解:当堂达标:
C384D类比小结小结:1.等比数列的定义:(1)归纳法;(2)累乘法.推导方法:2.等比数列的通项公式:公式的 认识:(1)函数的观点;(2)方程的思想.an=a1qn-1 3.等比中项:an=amqn-m 课后作业: 1、阅读教材第48~52页
2、完成课本第53页3,4题谢 谢 !
2.掌握等比数列的通项公式.会解决知道n, 中的三个,求另一个的问题.
学习重点:
1.等比数列概念的理解与掌握;
2.等比数列的通项公式的推导及应用.
课题导入课本P48页的4个例子:(1)细胞分裂问题(2)“一尺之棰,日取其半,万世不竭”(3)计算机病毒感染问题(4)银行复利计算问题①1,2,4,8,16,…②1,,,,,…③1,20,,,,…④,,,,……请同学们仔细观察一下,看看以上①、②、③、④
四个数列有什么共同特征?从第二项起,每一项与它前一项之比等于同一常数.探究一:等比数列的定义(1)1,2,22,23,…观察下列数列,说出它们的特点.定义:如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,记为q(q≠0).数学语言:探究一:等比数列的定义(判断一个数列是否为等比数列的依据)
1.已知等比数列{ an }:
(1) an 能不能是零?
(2)公比q能不能是1?
2.用下列方法表示的数列中能确定
是等比数列的是 .
① 1,-1,1,…,(-1)n+1 ; ②1,2,4,6…;
③a,a,a,…,a; ④已知a1=2,an=3an+1 ;
⑤
⑥2a,2a,2a,…,2a.
3.什么样的数列既是等差数列又是等比数列?不能能√√√×××非零的
常数列① ④ ⑥思考1:思考2:
若a,G,b三个数成等比数列,那么这 三个数有何恒等关系?结论:G2=abG叫做a,b的等比中项通项公式 数学式
子表示定 义等比数列 等差数列名 称如果一个数列从第2项起,每一项与前一项的差等于同一个常数,那么这个数列叫做等差数列.这个常数叫做等差数列的公差,用d表示an+1-an=dan = a1 +(n-1)d如果一个数列从第2项起,每一项与它前一项的比都等于同一个常数,那么这个数列叫做等比数列.这个常数叫做等比数列的公比,用q表示?等差中项等比中项探究二:通项公式思考3:如何用a1和q表示第n项an
a2/a1=q
a3/a2=q
a4/a3=q
…
an/an-1=q其中,a1与q均不为0。由于当n=1时上面等式两边均为a1,
即等式也成立,说明上面公式当n∈N*时都成立,因此它
就是等比数列{an}的通项公式。这n-1个式子相乘得an/a1=qn-1
所以 an=a1qn-1
1.叠乘法(累乘法)
a2=a1q
a3=a2q=a1q2
a4=a3q=a1q3
…
an=a1qn-12.不完全归纳法a1q2a1q3a1qn-1等比数列的通项公式:
(n∈N﹡,q≠0)例如:数列{an}的首项是a1=1,公比q=2,则通项公式是: ______上式还可以写成可见,这个等比数列
的图象都在函数
的图象上,如右图所示。 0 1 2 3 4 nan
8
7
6
5
4
3
2
1····思考4:等比数列的通项公式与函数有怎样的关系?世界杂交水稻之父—袁隆平从1976年至1999年在我国累计推广种植杂交水稻35亿多亩,增产稻谷3500亿公斤。年增稻谷可养活6000万人口。 西方世界称他的杂交稻是“东方魔稻” ,并认为是解决下个世纪世界性饥饿问题的法宝。接轨生活 袁隆平在培育某水稻新品种时,培育出第一代120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代时大约可以得到这个新品种的种子多少粒(保留两位有效数字)?由于每代的种子数是它的前一代种子数的120倍,因此,逐代的种子数组成等比数列,记为 答:到第5代大约可以得到这种新品种的种子2.5×1010粒.解:解:当堂达标:
C384D类比小结小结:1.等比数列的定义:(1)归纳法;(2)累乘法.推导方法:2.等比数列的通项公式:公式的 认识:(1)函数的观点;(2)方程的思想.an=a1qn-1 3.等比中项:an=amqn-m 课后作业: 1、阅读教材第48~52页
2、完成课本第53页3,4题谢 谢 !
