2017-2018学年人教A版必修2 1.1.1.1 棱柱 棱锥 棱台的结构特征 课件(28张)
文档属性
| 名称 | 2017-2018学年人教A版必修2 1.1.1.1 棱柱 棱锥 棱台的结构特征 课件(28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 810.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 00:00:00 | ||
图片预览







文档简介
课件28张PPT。第1课时 棱柱、棱锥、棱台的结构特征1.知道空间几何体的概念及其含义,了解空间几何体的分类及其相关概念.
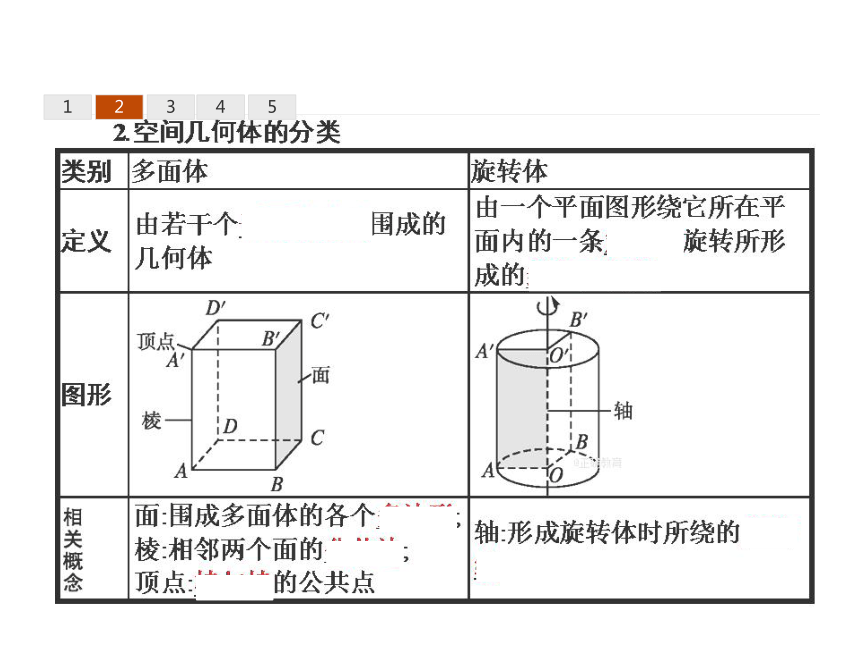
2.了解棱柱、棱锥、棱台的定义,知道这三种几何体的结构特征,能够识别和区分这些几何体.123451.空间几何体的定义
空间中的物体都占据着空间的一部分,如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.1234512345名师点拨 对多面体的理解,应注意以下几个方面:
(1)多面体是由平面多边形围成的,不是由圆面或其他曲面围成的,也不是由空间多边形围成的.
(2)本章所说的多边形,一般包括它内部的平面部分,故多面体是一个“封闭”的几何体.
(3)围成一个多面体至少需要四个面.
(4) 如果一个多面体是由几个面围成的,那么这个多面体就称为几面体.12345【做一做1】 下列物体不能抽象成旋转体的是( )
A.篮球 B.日光灯管
C.电线杆 D.金字塔
解析:金字塔是多面体,不能抽象成旋转体;篮球、日光灯管、电线杆都可抽象成旋转体.
答案:D123451234512345【做一做2】 下列说法正确的是( )
A.所有的棱柱都有一个底面
B.棱柱的顶点至少有6个
C.棱柱的侧棱至少有4条
D.棱柱的棱至少有4条
解析:因为棱柱有两个底面,所以A项不正确;因为棱柱底面的边数至少是3,棱柱的顶点数至少是6,棱柱的侧棱数至少是3,棱柱的棱数至少是9,所以C,D项不正确,B项正确.
答案:B123451234512345【做一做3】 下列棱锥有6个面的是( )
A.三棱锥 B.四棱锥
C.五棱锥 D.六棱锥
解析:三棱锥有4个面;四棱锥有5个面;五棱锥有6个面;六棱锥有7个面.
答案:C1234512345归纳总结1.棱台的侧棱延长后交于一点,侧面是梯形.
2.在棱台中,两个底面与平行于底面的截面是相似多边形,如图①所示.
3.在棱台中,过不相邻的两条侧棱的截面是梯形,如图②所示.12345【做一做4】 下列四个几何体是棱台的为( )
解析:A项中的几何体是棱柱;B项中的几何体是棱锥;D项中的几何体的侧棱没有交于一点,则它不是棱台;很明显C项中的几何体是棱台.
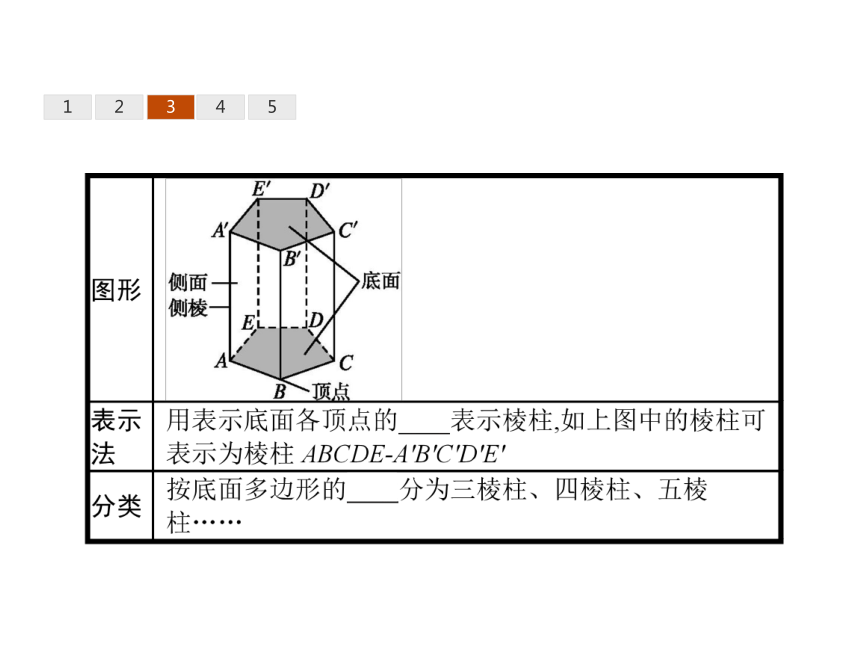
答案:C1231.识别棱柱
剖析:判断一个几何体是不是棱柱,关键是要紧扣棱柱的三个本质特征:
(1)有两个面互相平行;
(2)其余各面是平行四边形;
(3)在这些平行四边形中,每相邻两个面的公共边都互相平行.
这三个特征缺一不可,如图所示的几何体有两个面互相平行,其余各面都是平行四边形,但不具备特征(3),故不是棱柱.1232.识别棱锥
剖析:将图①所示的正方体ABCD-A1B1C1D1截去两个三棱锥A-A1B1D1和C1-B1CD1,得如图②所示的几何体.
图②所示的几何体有一个面ABCD是四边形,其余各面都是三角形,很明显这个几何体不是棱锥.因此,有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥.123由此看出,判断一个几何体是不是棱锥,关键是要紧扣棱锥的三个本质特征:
(1)有一个面是多边形;(2)其余各面是三角形;(3)这些三角形有一个公共顶点.这三个特征缺一不可.1233.棱柱、棱锥、棱台的结构特征比较
剖析:如下表所示.题型一题型二【例1】 下列说法不正确的是 .(只填序号)?
①棱台的侧面一定不会是平行四边形;
②一个底面是正方形的棱锥的侧棱长相等;
③棱柱的底面一定是平行四边形;
④棱柱中两个互相平行的面一定是棱柱的底面.题型一题型二解析:
棱台的侧面为梯形,故①正确;若ABCD-A1B1C1D1为正方体,则四棱锥A-A1B1C1D1的底面是正方形,但侧棱长不相等,故②不正确;易知③不正确;在如图所示的棱柱中,前、后两个面互相平行,但都不是底面,故④不正确.
答案:②③④题型一题型二反思棱柱、棱锥、棱台的定义是识别和区分多面体结构特征的关键.因此,在涉及多面体的结构特征问题时,先看是否满足定义,再看它们是否具备各自的性质.题型一题型二【变式训练1】 下列说法正确的有( )
①一个棱柱至少有五个面;②用一个平面去截棱锥,底面和截面之间的部分叫棱台;③棱台的侧面是等腰梯形;④各个面都是三角形的几何体是三棱锥.
A.1个 B.2个 C.3个 D.4个题型一题型二解析:
①中,因为棱柱有两个底面,所以棱柱的面数由侧面个数决定,而侧面个数与底面多边形的边数相等,所以面数最少的棱柱为三棱柱,有五个面,故①正确;②中,截面与底面不一定平行,故②不正确;③中,因为棱台是由棱锥截来的,而棱锥的所有侧棱不一定相等,所以棱台的侧棱不一定都相等,即不一定是等腰梯形,故③不正确;④中,如图所示的几何体各面均为三角形,但不是三棱锥,故④不正确.
答案:A题型一题型二【例2】 根据下列关于多面体结构特征的描述,说出多面体的名称:
(1)由6个平行四边形围成的几何体;
(2)由7个面围成,其中一个面是六边形,其余6个面都是有一个公共顶点的三角形.
解:(1)棱锥的侧面形状只能是三角形,则该多面体不是棱锥;棱台的侧面形状是梯形,则该多面体不是棱台,所以该几何体只能是棱柱.由6个面均是平行四边形,知该棱柱的底面是平行四边形,即该几何体是底面为平行四边形的四棱柱.
(2)棱柱和棱台的面中有0个或2个面是三角形(即底面),则该多面体不是棱柱和棱台,而是棱锥.这6个三角形是侧面,六边形是底面,即该棱锥是六棱锥.题型一题型二反思根据多面体的特征描述识别和判断多面体时,要结合棱柱、棱锥、棱台的结构特征(侧面形状、底面形状、侧棱、底边等)来确定.注意判断时要充分发挥空间想象能力,必要时做出几何模型通过演示进行准确判断.题型一题型二【变式训练2】 如图,观察下面四个几何体,其中判断正确的是( )
A.①是棱台
B.②是棱台
C.③是棱锥
D.④不是棱柱题型一题型二解析:①不是由棱锥截来的,所以①不是棱台;②上、下两个底面不平行,所以②不是棱台;③是棱锥;④前、后两个面平行,其他的面都是平行四边形,且相邻两个平行四边形的公共边互相平行,所以④是棱柱,故选C.
答案:C
2.了解棱柱、棱锥、棱台的定义,知道这三种几何体的结构特征,能够识别和区分这些几何体.123451.空间几何体的定义
空间中的物体都占据着空间的一部分,如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.1234512345名师点拨 对多面体的理解,应注意以下几个方面:
(1)多面体是由平面多边形围成的,不是由圆面或其他曲面围成的,也不是由空间多边形围成的.
(2)本章所说的多边形,一般包括它内部的平面部分,故多面体是一个“封闭”的几何体.
(3)围成一个多面体至少需要四个面.
(4) 如果一个多面体是由几个面围成的,那么这个多面体就称为几面体.12345【做一做1】 下列物体不能抽象成旋转体的是( )
A.篮球 B.日光灯管
C.电线杆 D.金字塔
解析:金字塔是多面体,不能抽象成旋转体;篮球、日光灯管、电线杆都可抽象成旋转体.
答案:D123451234512345【做一做2】 下列说法正确的是( )
A.所有的棱柱都有一个底面
B.棱柱的顶点至少有6个
C.棱柱的侧棱至少有4条
D.棱柱的棱至少有4条
解析:因为棱柱有两个底面,所以A项不正确;因为棱柱底面的边数至少是3,棱柱的顶点数至少是6,棱柱的侧棱数至少是3,棱柱的棱数至少是9,所以C,D项不正确,B项正确.
答案:B123451234512345【做一做3】 下列棱锥有6个面的是( )
A.三棱锥 B.四棱锥
C.五棱锥 D.六棱锥
解析:三棱锥有4个面;四棱锥有5个面;五棱锥有6个面;六棱锥有7个面.
答案:C1234512345归纳总结1.棱台的侧棱延长后交于一点,侧面是梯形.
2.在棱台中,两个底面与平行于底面的截面是相似多边形,如图①所示.
3.在棱台中,过不相邻的两条侧棱的截面是梯形,如图②所示.12345【做一做4】 下列四个几何体是棱台的为( )
解析:A项中的几何体是棱柱;B项中的几何体是棱锥;D项中的几何体的侧棱没有交于一点,则它不是棱台;很明显C项中的几何体是棱台.
答案:C1231.识别棱柱
剖析:判断一个几何体是不是棱柱,关键是要紧扣棱柱的三个本质特征:
(1)有两个面互相平行;
(2)其余各面是平行四边形;
(3)在这些平行四边形中,每相邻两个面的公共边都互相平行.
这三个特征缺一不可,如图所示的几何体有两个面互相平行,其余各面都是平行四边形,但不具备特征(3),故不是棱柱.1232.识别棱锥
剖析:将图①所示的正方体ABCD-A1B1C1D1截去两个三棱锥A-A1B1D1和C1-B1CD1,得如图②所示的几何体.
图②所示的几何体有一个面ABCD是四边形,其余各面都是三角形,很明显这个几何体不是棱锥.因此,有一个面是多边形,其余各面都是三角形的几何体不一定是棱锥.123由此看出,判断一个几何体是不是棱锥,关键是要紧扣棱锥的三个本质特征:
(1)有一个面是多边形;(2)其余各面是三角形;(3)这些三角形有一个公共顶点.这三个特征缺一不可.1233.棱柱、棱锥、棱台的结构特征比较
剖析:如下表所示.题型一题型二【例1】 下列说法不正确的是 .(只填序号)?
①棱台的侧面一定不会是平行四边形;
②一个底面是正方形的棱锥的侧棱长相等;
③棱柱的底面一定是平行四边形;
④棱柱中两个互相平行的面一定是棱柱的底面.题型一题型二解析:
棱台的侧面为梯形,故①正确;若ABCD-A1B1C1D1为正方体,则四棱锥A-A1B1C1D1的底面是正方形,但侧棱长不相等,故②不正确;易知③不正确;在如图所示的棱柱中,前、后两个面互相平行,但都不是底面,故④不正确.
答案:②③④题型一题型二反思棱柱、棱锥、棱台的定义是识别和区分多面体结构特征的关键.因此,在涉及多面体的结构特征问题时,先看是否满足定义,再看它们是否具备各自的性质.题型一题型二【变式训练1】 下列说法正确的有( )
①一个棱柱至少有五个面;②用一个平面去截棱锥,底面和截面之间的部分叫棱台;③棱台的侧面是等腰梯形;④各个面都是三角形的几何体是三棱锥.
A.1个 B.2个 C.3个 D.4个题型一题型二解析:
①中,因为棱柱有两个底面,所以棱柱的面数由侧面个数决定,而侧面个数与底面多边形的边数相等,所以面数最少的棱柱为三棱柱,有五个面,故①正确;②中,截面与底面不一定平行,故②不正确;③中,因为棱台是由棱锥截来的,而棱锥的所有侧棱不一定相等,所以棱台的侧棱不一定都相等,即不一定是等腰梯形,故③不正确;④中,如图所示的几何体各面均为三角形,但不是三棱锥,故④不正确.
答案:A题型一题型二【例2】 根据下列关于多面体结构特征的描述,说出多面体的名称:
(1)由6个平行四边形围成的几何体;
(2)由7个面围成,其中一个面是六边形,其余6个面都是有一个公共顶点的三角形.
解:(1)棱锥的侧面形状只能是三角形,则该多面体不是棱锥;棱台的侧面形状是梯形,则该多面体不是棱台,所以该几何体只能是棱柱.由6个面均是平行四边形,知该棱柱的底面是平行四边形,即该几何体是底面为平行四边形的四棱柱.
(2)棱柱和棱台的面中有0个或2个面是三角形(即底面),则该多面体不是棱柱和棱台,而是棱锥.这6个三角形是侧面,六边形是底面,即该棱锥是六棱锥.题型一题型二反思根据多面体的特征描述识别和判断多面体时,要结合棱柱、棱锥、棱台的结构特征(侧面形状、底面形状、侧棱、底边等)来确定.注意判断时要充分发挥空间想象能力,必要时做出几何模型通过演示进行准确判断.题型一题型二【变式训练2】 如图,观察下面四个几何体,其中判断正确的是( )
A.①是棱台
B.②是棱台
C.③是棱锥
D.④不是棱柱题型一题型二解析:①不是由棱锥截来的,所以①不是棱台;②上、下两个底面不平行,所以②不是棱台;③是棱锥;④前、后两个面平行,其他的面都是平行四边形,且相邻两个平行四边形的公共边互相平行,所以④是棱柱,故选C.
答案:C
