2017-2018学年人教A版必修二 2.1.1 平面 课件(23张)
文档属性
| 名称 | 2017-2018学年人教A版必修二 2.1.1 平面 课件(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 12:39:32 | ||
图片预览








文档简介
课件23张PPT。§2.1.1 平 面学习目标 1、了解平面的概念及表示方法;
2、理解平面的公理1、公理2、公理3;
3、会用符号语言准确表述几何对象的位置关系.重点:1、用符号语言描述空间点、直线、平面之间的 位置关系; 2、用三种语言描述三个公理及三个公理的应用. 难点:1、平面的概念; 2、三个公理的应用. 自学导引1、自学课本第40页至41页思考上面(时间3分钟)
2、思考下面问题:
(1)如何形容平面?
(2)平面的表示方法?
(3)点、直线、平面之间的位置关系是什么?1、平面桌面黑板面平静的水面平面的形象(1)几何里的平面是平滑,无厚度,可无限延展的.检查自学效果(2)平面与平面无大小,厚薄之分,只有位置上的
不同.如:重合,相交,平行,垂直.2、平面的表示法①平面通常用一个希腊字母α、β、γ等来表示,如:平面α、平面β、平面γ;
②用表示平行四边形的四个顶点或两个相对顶点的字母来表示,如平面ABCD或平面AC、平面BD.检查自学效果常常把水平的平面画成锐角为450,横边长等于其邻边长2倍的平行四边形.3、相交平面的画法如果一个平面被另一个平面挡住,
则这遮挡的部分用虚线画出来.检查自学效果判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
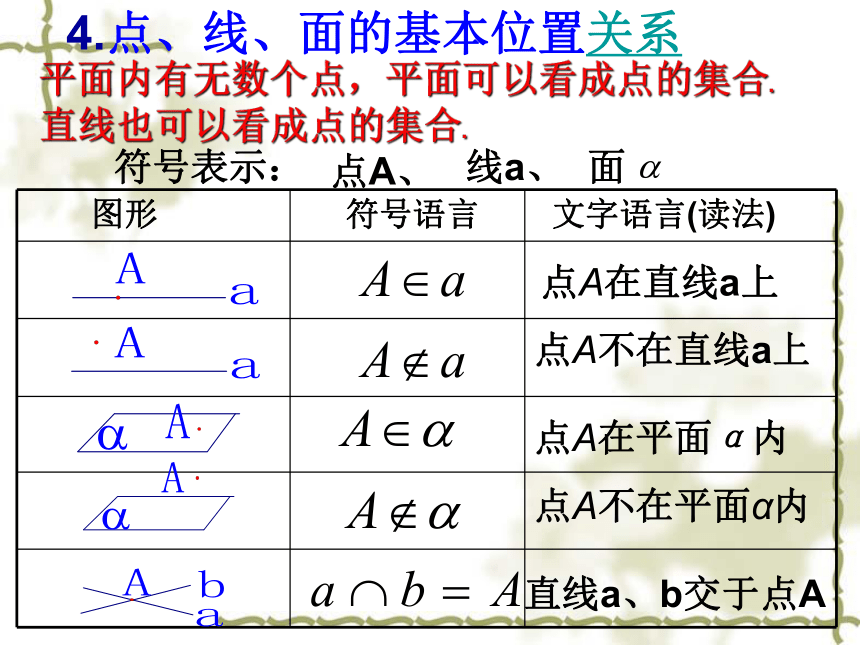
5、一个平面可以把空间分成两部分. ( )练习当堂训练点A在直线a上点A不在直线a上点A在平面α内 点A不在平面α内 直线a、b交于点A 4.点、线、面的基本位置关系符号表示:点A、 线a、面平面内有无数个点,平面可以看成点的集合.直线也可以看成点的集合.直线a在平面 内直线a与平面
无公共点直线a与平面
交于点A平面 与
相交于直线思考文字语言图形语言符号语言B··A·..公理1 如果一条直线上的两点在一个平面
内,那么这条直线在此平面内.思考为什么有的自行车后轮旁只安装一只撑脚?文字语言图形语言 公理2 过不在一条直线上的三点,
有且只有一个平面.符号语言α·A·B·C思考把三角板的一个角立在课桌面上,三角板所在平面
与桌面所在平面是否只相交于一点?为什么?文字语言图形语言符号语言公理3:如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.αβ公理1 如果一条直线上的两点在一个平面内, 那么这条直线在此平面内.公理3 如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共 直线.公理2 过不在一条直线上的三点,有且只有一 个平面.5、平面的基本性质经过一条直线和直线外一点,有且只有一个平面经过不共线的三点有且只有一个平面公理2推论2平面的确定推论3推论1经过两条相交直线,有且只有一个平面经过两条平行直线,有且只有一个平面②四条线段顺次首尾连接,所得的图形一定是平面图形吗?
为什么?练习①三角形、梯形是否一定是平面图形?为什么?1、平面的特点;
2、平面的画法;
3、三种语言之间的转换;
4、三公理三推论.课堂小结课堂作业课本P43
第4题证明三线共面,可先证其中两条直线共面,再证第三条直线也在此平面内.例1.一条直线和两条平行线都相交,求证:这三条直线共面.αBAabl已知:如图,a∥b,l∩ a =A, l ∩b =B求证:a,b,l三线共面证明:∵ a∥b,由公理2推论3有
直线a,b确定一个平面α∴ a,b,l三线共面于α例2.已知:如图D,E分别是ΔABC的边AC,BC上的点,平面α经过D,E两点.
(1)求作直线AB与平面α的交点P;αABCDEP(2)求证:D,E,P三点共线.例3.如图,P,Q是正方体ABCD-A1B1C1D1的棱AB,BC的中点,过P,Q,D1作一个平面,画出此平面截正方体的截面.ABCDA1B1C1D1PQ
2、理解平面的公理1、公理2、公理3;
3、会用符号语言准确表述几何对象的位置关系.重点:1、用符号语言描述空间点、直线、平面之间的 位置关系; 2、用三种语言描述三个公理及三个公理的应用. 难点:1、平面的概念; 2、三个公理的应用. 自学导引1、自学课本第40页至41页思考上面(时间3分钟)
2、思考下面问题:
(1)如何形容平面?
(2)平面的表示方法?
(3)点、直线、平面之间的位置关系是什么?1、平面桌面黑板面平静的水面平面的形象(1)几何里的平面是平滑,无厚度,可无限延展的.检查自学效果(2)平面与平面无大小,厚薄之分,只有位置上的
不同.如:重合,相交,平行,垂直.2、平面的表示法①平面通常用一个希腊字母α、β、γ等来表示,如:平面α、平面β、平面γ;
②用表示平行四边形的四个顶点或两个相对顶点的字母来表示,如平面ABCD或平面AC、平面BD.检查自学效果常常把水平的平面画成锐角为450,横边长等于其邻边长2倍的平行四边形.3、相交平面的画法如果一个平面被另一个平面挡住,
则这遮挡的部分用虚线画出来.检查自学效果判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( )练习当堂训练点A在直线a上点A不在直线a上点A在平面α内 点A不在平面α内 直线a、b交于点A 4.点、线、面的基本位置关系符号表示:点A、 线a、面平面内有无数个点,平面可以看成点的集合.直线也可以看成点的集合.直线a在平面 内直线a与平面
无公共点直线a与平面
交于点A平面 与
相交于直线思考文字语言图形语言符号语言B··A·..公理1 如果一条直线上的两点在一个平面
内,那么这条直线在此平面内.思考为什么有的自行车后轮旁只安装一只撑脚?文字语言图形语言 公理2 过不在一条直线上的三点,
有且只有一个平面.符号语言α·A·B·C思考把三角板的一个角立在课桌面上,三角板所在平面
与桌面所在平面是否只相交于一点?为什么?文字语言图形语言符号语言公理3:如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.αβ公理1 如果一条直线上的两点在一个平面内, 那么这条直线在此平面内.公理3 如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共 直线.公理2 过不在一条直线上的三点,有且只有一 个平面.5、平面的基本性质经过一条直线和直线外一点,有且只有一个平面经过不共线的三点有且只有一个平面公理2推论2平面的确定推论3推论1经过两条相交直线,有且只有一个平面经过两条平行直线,有且只有一个平面②四条线段顺次首尾连接,所得的图形一定是平面图形吗?
为什么?练习①三角形、梯形是否一定是平面图形?为什么?1、平面的特点;
2、平面的画法;
3、三种语言之间的转换;
4、三公理三推论.课堂小结课堂作业课本P43
第4题证明三线共面,可先证其中两条直线共面,再证第三条直线也在此平面内.例1.一条直线和两条平行线都相交,求证:这三条直线共面.αBAabl已知:如图,a∥b,l∩ a =A, l ∩b =B求证:a,b,l三线共面证明:∵ a∥b,由公理2推论3有
直线a,b确定一个平面α∴ a,b,l三线共面于α例2.已知:如图D,E分别是ΔABC的边AC,BC上的点,平面α经过D,E两点.
(1)求作直线AB与平面α的交点P;αABCDEP(2)求证:D,E,P三点共线.例3.如图,P,Q是正方体ABCD-A1B1C1D1的棱AB,BC的中点,过P,Q,D1作一个平面,画出此平面截正方体的截面.ABCDA1B1C1D1PQ
