吉林省长春汽车经济技术开发区2017_2018学年高二数学9月月考试题理
文档属性
| 名称 | 吉林省长春汽车经济技术开发区2017_2018学年高二数学9月月考试题理 |

|
|
| 格式 | zip | ||
| 文件大小 | 455.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-12 00:00:00 | ||
图片预览




文档简介
高二年级2017~2018学年度上学期月考考试
数学(理)学科
考试说明:
1.考试时间为120分钟,满分150分,选择题涂卡。
2.考试完毕交答题卡。
第Ⅰ卷
一、选择题(本题包括12个小题,每小题只有一个正确选项,每小题5分,共60分)
1.圆的圆心坐标与半径是(
)
A.
B.
C.
D.
2.《九章算术》中介绍了一种“更相减损术”,用于求两个正整数的最大公约数,将该方法用算法流程图表示如下,若输入,
,则输出的结果为(
)
A.
,
B.
,
C.
,
D.
,
3.圆与圆的位置关系是(
)
A.
外离
B.
外切
C.
相交
D.
内切
4.登山族为了了解某山高与气温之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
气温
18
13
10
山高
24
34
38
64
由表中数据,得到线性回归方程为,由此估计山高为处气温的度数为(
)
A.
B.
C.
D.
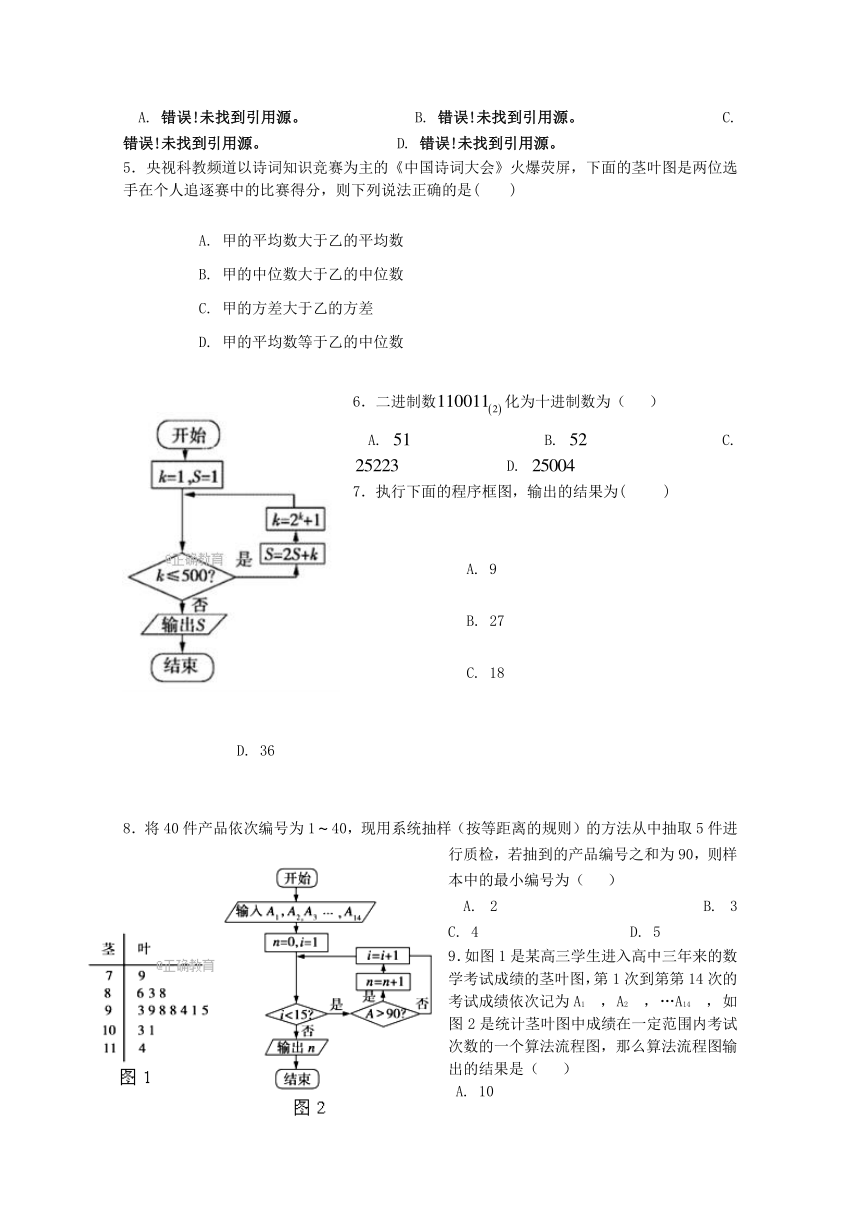
5.央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,下面的茎叶图是两位选手在个人追逐赛中的比赛得分,则下列说法正确的是(
)
A.
甲的平均数大于乙的平均数
B.
甲的中位数大于乙的中位数
C.
甲的方差大于乙的方差
D.
甲的平均数等于乙的中位数
6.二进制数化为十进制数为(
)
A.
B.
C.
D.
7.执行下面的程序框图,输出的结果为(
)
A.
9
B.
27
C.
18
D.
36
8.将40件产品依次编号为140,现用系统抽样(按等距离的规则)的方法从中抽取5件进行质检,若抽到的产品编号之和为90,则样本中的最小编号为(
)
A.
2
B.
3
C.
4
D.
5
9.如图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第第14次的考试成绩依次记为A1
,
A2
,
…A14
,
如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图,那么算法流程图输出的结果是(
)
A.
10
B.
9
C.
8
D.
7
10.由直线上的一点向圆引切线,则切线长的最小值为(
)
A.
B.
C.
D.
11.如图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是(
)
A.
B.
C.
D.
12.曲线y=1+
[-2,2])与直线y=k(x-2)+4有两个公共点时,实数k的取值范围是(
)
A.
B.
C.
D.
第Ⅱ卷
二、填空题(本题包括4个小题,共20分)
13.在空间直角坐标系中,已知,,则_____________.
14.设某总体是由编号为01,02,…,39,40的40个个体组成的,利用下面的随机数表依次选取4个个体,选取方法是从随机数表第一行的第三列数字开始从左到右依次选取两个数字,则选出来的第4个个体的编号为_____________.
0618
0765
4544
1816
5809
7983
8619
7606
8350
0310
5923
4605
0526
6238
15.经过原点并且与直线相切于点的圆的标准方程是_____________.
16.已知直线与圆相交于两点,点分别在圆
上运动,且位于直线两侧,则四边形面积的最大值为_____________.
三、简答题(本题包括6个小题,共70分)
17.(满分10分)已知圆过三点,圆.
(1)求圆的方程;
(2)如果圆和圆相外切,求实数的值.
18.(满分12分)每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间
(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(1)求的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为,
的两组中各抽取多少人?
19.(满分12分)
已知等差数列,
(1)求的通项公式;
(2)令,求数列的前项和.
20.(满分12分)已知为三个内角的对边,且.
(1)求;
(2)若,
的面积为,求与的值.
21.(满分12分)
已知圆,直线经过点A
(1,0).
(1)若直线与圆C相切,求直线的方程;
(2)若直线与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线的方程.
22.(满分12分)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F为CD中点.
(1)求证:EF⊥平面BCD;
(2)求二面角C-DE-A的大小.
参考答案
1.D
【解析】圆方程可化为圆心,半径,故选D.
2.A
【解析】输入时,是,,此时是,,否,,否,是,输出,结束,选A.
3.C
【解析】由得,两圆的圆心距为,两圆的半径分别为,由于,则两圆相交,选C.
4.C
【解析】由题意,==10,==40,
代入到线性回归方程,可得=60,
∴y = 2x+60,
∴由= 2x+60=72,可得x= 6,
故选:C.
5.C
【解析】由茎叶图,知:
,
,
,
,
甲的中位数为:26,乙的中位数为:28,
∴甲的方差大于乙的方差。
本题选择C选项.
6.A
【解析】
,故选A.
7.B
【解析】第一次循环:,
第二次循环:
第三次循环:故输出结果为27
故选B
8.A
【解析】该系统抽样的抽取间隔为=8;
设抽到的最小编号x,
则x+(8+x)+(16+x)+(24+x)+(32+x)=90,
所以x=2.
故选:A.
9.A
【解析】该程序的作用是累加14次考试成绩超过90分的人数;
根据茎叶图的含义可得超过90分的人数为10个
本题选择A选项.
点睛:识别、运行程序框图和完善程序框图的思路
(1)要明确程序框图的顺序结构、条件结构和循环结构.
(2)要识别、运行程序框图,理解框图所解决的实际问题.
(3)按照题目的要求完成解答并验证.
10.C
【解析】试题分析:圆的圆心为,圆心到直线的距离为,所以由勾股定理可知切线长的最小值为
考点:直线与圆相切问题
11.A
【解析】由题意,框图首先给累加变量赋值为赋值,给循环变量赋值,
由算法的功能是计算的值,
得跳出循环的的值为,所以判断框的条件为或都可以,故选A.
12.D
【解析】曲线y=1+
[-2,2])表示圆的一部分,
直线y=k(x 2)+4是过定点(2、4)的直线系,
如图:不难看出直线的斜率范围是
故选D.
点睛:已知函数有零点求参数取值范围常用的方法和思路
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
13.
【解析】由两点之间距离公式可得:
.
14.09
【解析】随机数表法从指定位置找出的数字应该不超过编号的符号,按其要求选出的编号应为其中重复删去,第个个体的编号为.
15.
【解析】设圆心坐标,则,,,根据这三个方程组可以计算得:,所以所求方程为:
点睛:设出圆心与半径,根据题意列出方程组,解出圆心和半径即可
16.
【解析】把圆M:x2+y2 2x+2y 1=0化为标准方程:(x 1)2+(y+1)2=3,圆心(1, 1),半径
.
直线与圆相交,由点到直线的距离公式的弦心距,
由勾股定理的半弦长=
,所以弦长
.
又B,D两点在圆上,并且位于直线l的两侧,四边形ABCD的面积可以看成是两个三角形△ABC和△ACD的面积之和,
如图所示,
当B,D为如图所示位置,即BD为弦AC的垂直平分线时(即为直径时),两三角形的面积之和最大,即四边形ABCD的面积最大,
最大面积为:
.
点睛:直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的.判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,则用几何法;若方程中含有参数,或圆心到直线的距离的表达较繁琐,则用代数法.
17.(1)(2)
【解析】试题分析:(1)设圆一般方程,代入三点坐标,解方程组可得,(2)先化圆的标准方程,再由两圆外切得,解方程可得实数的值.
试题解析:解:(1)设圆的方程为,
因为圆过三点,
所以,
解得,
所以圆的方程为.
(2)圆的方程即,所以圆心,半径为5,
圆即,
所以圆心,半径为2.
因为圆和圆外切,所以,所以,
解得.
18.(1)
;(2)
;(3)
阅读时间在分钟的应选人,
阅读时间在分钟的应选人.
【解析】试题分析:(1)由频率分布直方图的性质易得:(2)由频率分布直方图确定平均数;(3)根据分层抽样性质确定抽取人数.
试题解析:
(1)由已知,得,
解得.
(2)由样本的频率分布直方图,估计该学校所有学生在这一天的平均阅读时间为:
(分钟).
(3)阅读时间在分钟的人数为,
阅读时间在分钟的人数为,
用分层抽样选人的抽样比为,
∴阅读时间在分钟的应选人,
阅读时间在分钟的应选人.
点睛:利用频率分布直方图求众数、中位数与平均数时,易出错,应注意区分这三者.在频率分布直方图中:
(1)最高的小长方形底边中点的横坐标即是众数;
(2)中位数左边和右边的小长方形的面积和是相等的;
(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
19.(1)(2)
【解析】(1)设数列的公差为d,依题意得方程组
解得
所以的通项公式为
(2)由得,
因为,所以是首项,公式的等比数列.
于是得的前n项和
20.(1);(2)或.
【解析】试题分析:(1)利用正弦定理将边长和角进行转化,将已知等式中涉及的边和角的组合等式根据题目所要求的内容化为角或者边,本题要求,故全部化为角的等式,从而求出.
(2)利用求得b,c的一个方程,再利用余弦定理得到第二个方程,两个方程两个未知数,解出b,c的值.
试题解析:(1)∵,由正弦定理得:
,即
,
化简得:,∴
在中,,∴,得,
(2)由已知得,可得,
由已知及余弦定理得,,,
联立方程组,可得或.
21.(1)或(2)y=x-1或y=7x-7
【解析】试题分析:(1)由直线与圆相切可得圆心(3,4)到已知直线的距离等于半径2,设直线点斜式方程,列方程可得斜率,最后验证斜率不存在时是否满足条件(2)由垂径定理可得弦长PQ,而三角形的高为圆心到直线的距离d,所以,利用基本不等式求最值可得当d=时,S取得最小值2,再根据点到直线距离公式求直线的斜率,即得的方程.
试题解析:(1)①若直线的斜率不存在,则直线,符合题意.
②若直线斜率存在,设直线为,即.
由题意知,圆心(3,4)到已知直线的距离等于半径2,
即,解得,
所求直线方程为,或;
(2)直线与圆相交,斜率必定存在,且不为0,设直线方程为,
则圆心到直线的距离,
又∵三角形面积
∴当d=时,S取得最小值2,则,,
故直线方程为y=x-1,或y=7x-7.
点睛:与圆有关的最值问题主要表现在求几何图形的长度、面积的最值,求点到直线的距离的最值,求相关参数的最值等方面.解决此类问题的主要思路是利用圆的几何性质将问题转化.涉及圆中弦长问题,一般利用垂径定理进行解决,具体就是利用半径的平方等于圆心到直线距离平方与弦长一半平方的和
22.(Ⅰ)取BC中点G点,连接AG,FG,F,G分别为DC,BC中点,
得到平面ABC⊥平面BCD,
G为
BC中点,且AC=AB,推出AG⊥BC,从而AG⊥平面BCD,
EF⊥平面BCD.
(Ⅱ)二面角C-DE-A的大小为
【解析】
试题分析:(Ⅰ)取BC中点G点,连接AG,FG,
∵F,G分别为DC,BC中点,
∴FG∥BD且FG=BD,又AE∥BD且AE=BD,
∴AE∥FG且AE=FG,∴四边形EFGA为平行四边形,
∴EF∥AG,∵AE⊥平面ABC,AE∥BD,
BD⊥平面ABC,又∵DB平面BCD,
平面ABC⊥平面BCD,∵G为
BC中点,且AC=AB,
∴AG⊥BC,∴AG⊥平面BCD,
∴EF⊥平面BCD.
6分
(Ⅱ)取AB的中点O和DE的中点H,分别以、、所在直线为x、y、z轴建立如图空间直角坐标系,设,则,,,,,.
设面CDE的法向量,则
取,
8分
取面ABDE的法向量,
10分
由,
故二面角C-DE-A的大小为.
12分
考点:本题主要考查立体几何中的垂直关系、角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。
数学(理)学科
考试说明:
1.考试时间为120分钟,满分150分,选择题涂卡。
2.考试完毕交答题卡。
第Ⅰ卷
一、选择题(本题包括12个小题,每小题只有一个正确选项,每小题5分,共60分)
1.圆的圆心坐标与半径是(
)
A.
B.
C.
D.
2.《九章算术》中介绍了一种“更相减损术”,用于求两个正整数的最大公约数,将该方法用算法流程图表示如下,若输入,
,则输出的结果为(
)
A.
,
B.
,
C.
,
D.
,
3.圆与圆的位置关系是(
)
A.
外离
B.
外切
C.
相交
D.
内切
4.登山族为了了解某山高与气温之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
气温
18
13
10
山高
24
34
38
64
由表中数据,得到线性回归方程为,由此估计山高为处气温的度数为(
)
A.
B.
C.
D.
5.央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,下面的茎叶图是两位选手在个人追逐赛中的比赛得分,则下列说法正确的是(
)
A.
甲的平均数大于乙的平均数
B.
甲的中位数大于乙的中位数
C.
甲的方差大于乙的方差
D.
甲的平均数等于乙的中位数
6.二进制数化为十进制数为(
)
A.
B.
C.
D.
7.执行下面的程序框图,输出的结果为(
)
A.
9
B.
27
C.
18
D.
36
8.将40件产品依次编号为140,现用系统抽样(按等距离的规则)的方法从中抽取5件进行质检,若抽到的产品编号之和为90,则样本中的最小编号为(
)
A.
2
B.
3
C.
4
D.
5
9.如图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,第1次到第第14次的考试成绩依次记为A1
,
A2
,
…A14
,
如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图,那么算法流程图输出的结果是(
)
A.
10
B.
9
C.
8
D.
7
10.由直线上的一点向圆引切线,则切线长的最小值为(
)
A.
B.
C.
D.
11.如图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是(
)
A.
B.
C.
D.
12.曲线y=1+
[-2,2])与直线y=k(x-2)+4有两个公共点时,实数k的取值范围是(
)
A.
B.
C.
D.
第Ⅱ卷
二、填空题(本题包括4个小题,共20分)
13.在空间直角坐标系中,已知,,则_____________.
14.设某总体是由编号为01,02,…,39,40的40个个体组成的,利用下面的随机数表依次选取4个个体,选取方法是从随机数表第一行的第三列数字开始从左到右依次选取两个数字,则选出来的第4个个体的编号为_____________.
0618
0765
4544
1816
5809
7983
8619
7606
8350
0310
5923
4605
0526
6238
15.经过原点并且与直线相切于点的圆的标准方程是_____________.
16.已知直线与圆相交于两点,点分别在圆
上运动,且位于直线两侧,则四边形面积的最大值为_____________.
三、简答题(本题包括6个小题,共70分)
17.(满分10分)已知圆过三点,圆.
(1)求圆的方程;
(2)如果圆和圆相外切,求实数的值.
18.(满分12分)每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间
(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(1)求的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为,
的两组中各抽取多少人?
19.(满分12分)
已知等差数列,
(1)求的通项公式;
(2)令,求数列的前项和.
20.(满分12分)已知为三个内角的对边,且.
(1)求;
(2)若,
的面积为,求与的值.
21.(满分12分)
已知圆,直线经过点A
(1,0).
(1)若直线与圆C相切,求直线的方程;
(2)若直线与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线的方程.
22.(满分12分)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F为CD中点.
(1)求证:EF⊥平面BCD;
(2)求二面角C-DE-A的大小.
参考答案
1.D
【解析】圆方程可化为圆心,半径,故选D.
2.A
【解析】输入时,是,,此时是,,否,,否,是,输出,结束,选A.
3.C
【解析】由得,两圆的圆心距为,两圆的半径分别为,由于,则两圆相交,选C.
4.C
【解析】由题意,==10,==40,
代入到线性回归方程,可得=60,
∴y = 2x+60,
∴由= 2x+60=72,可得x= 6,
故选:C.
5.C
【解析】由茎叶图,知:
,
,
,
,
甲的中位数为:26,乙的中位数为:28,
∴甲的方差大于乙的方差。
本题选择C选项.
6.A
【解析】
,故选A.
7.B
【解析】第一次循环:,
第二次循环:
第三次循环:故输出结果为27
故选B
8.A
【解析】该系统抽样的抽取间隔为=8;
设抽到的最小编号x,
则x+(8+x)+(16+x)+(24+x)+(32+x)=90,
所以x=2.
故选:A.
9.A
【解析】该程序的作用是累加14次考试成绩超过90分的人数;
根据茎叶图的含义可得超过90分的人数为10个
本题选择A选项.
点睛:识别、运行程序框图和完善程序框图的思路
(1)要明确程序框图的顺序结构、条件结构和循环结构.
(2)要识别、运行程序框图,理解框图所解决的实际问题.
(3)按照题目的要求完成解答并验证.
10.C
【解析】试题分析:圆的圆心为,圆心到直线的距离为,所以由勾股定理可知切线长的最小值为
考点:直线与圆相切问题
11.A
【解析】由题意,框图首先给累加变量赋值为赋值,给循环变量赋值,
由算法的功能是计算的值,
得跳出循环的的值为,所以判断框的条件为或都可以,故选A.
12.D
【解析】曲线y=1+
[-2,2])表示圆的一部分,
直线y=k(x 2)+4是过定点(2、4)的直线系,
如图:不难看出直线的斜率范围是
故选D.
点睛:已知函数有零点求参数取值范围常用的方法和思路
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
13.
【解析】由两点之间距离公式可得:
.
14.09
【解析】随机数表法从指定位置找出的数字应该不超过编号的符号,按其要求选出的编号应为其中重复删去,第个个体的编号为.
15.
【解析】设圆心坐标,则,,,根据这三个方程组可以计算得:,所以所求方程为:
点睛:设出圆心与半径,根据题意列出方程组,解出圆心和半径即可
16.
【解析】把圆M:x2+y2 2x+2y 1=0化为标准方程:(x 1)2+(y+1)2=3,圆心(1, 1),半径
.
直线与圆相交,由点到直线的距离公式的弦心距,
由勾股定理的半弦长=
,所以弦长
.
又B,D两点在圆上,并且位于直线l的两侧,四边形ABCD的面积可以看成是两个三角形△ABC和△ACD的面积之和,
如图所示,
当B,D为如图所示位置,即BD为弦AC的垂直平分线时(即为直径时),两三角形的面积之和最大,即四边形ABCD的面积最大,
最大面积为:
.
点睛:直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的.判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,则用几何法;若方程中含有参数,或圆心到直线的距离的表达较繁琐,则用代数法.
17.(1)(2)
【解析】试题分析:(1)设圆一般方程,代入三点坐标,解方程组可得,(2)先化圆的标准方程,再由两圆外切得,解方程可得实数的值.
试题解析:解:(1)设圆的方程为,
因为圆过三点,
所以,
解得,
所以圆的方程为.
(2)圆的方程即,所以圆心,半径为5,
圆即,
所以圆心,半径为2.
因为圆和圆外切,所以,所以,
解得.
18.(1)
;(2)
;(3)
阅读时间在分钟的应选人,
阅读时间在分钟的应选人.
【解析】试题分析:(1)由频率分布直方图的性质易得:(2)由频率分布直方图确定平均数;(3)根据分层抽样性质确定抽取人数.
试题解析:
(1)由已知,得,
解得.
(2)由样本的频率分布直方图,估计该学校所有学生在这一天的平均阅读时间为:
(分钟).
(3)阅读时间在分钟的人数为,
阅读时间在分钟的人数为,
用分层抽样选人的抽样比为,
∴阅读时间在分钟的应选人,
阅读时间在分钟的应选人.
点睛:利用频率分布直方图求众数、中位数与平均数时,易出错,应注意区分这三者.在频率分布直方图中:
(1)最高的小长方形底边中点的横坐标即是众数;
(2)中位数左边和右边的小长方形的面积和是相等的;
(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
19.(1)(2)
【解析】(1)设数列的公差为d,依题意得方程组
解得
所以的通项公式为
(2)由得,
因为,所以是首项,公式的等比数列.
于是得的前n项和
20.(1);(2)或.
【解析】试题分析:(1)利用正弦定理将边长和角进行转化,将已知等式中涉及的边和角的组合等式根据题目所要求的内容化为角或者边,本题要求,故全部化为角的等式,从而求出.
(2)利用求得b,c的一个方程,再利用余弦定理得到第二个方程,两个方程两个未知数,解出b,c的值.
试题解析:(1)∵,由正弦定理得:
,即
,
化简得:,∴
在中,,∴,得,
(2)由已知得,可得,
由已知及余弦定理得,,,
联立方程组,可得或.
21.(1)或(2)y=x-1或y=7x-7
【解析】试题分析:(1)由直线与圆相切可得圆心(3,4)到已知直线的距离等于半径2,设直线点斜式方程,列方程可得斜率,最后验证斜率不存在时是否满足条件(2)由垂径定理可得弦长PQ,而三角形的高为圆心到直线的距离d,所以,利用基本不等式求最值可得当d=时,S取得最小值2,再根据点到直线距离公式求直线的斜率,即得的方程.
试题解析:(1)①若直线的斜率不存在,则直线,符合题意.
②若直线斜率存在,设直线为,即.
由题意知,圆心(3,4)到已知直线的距离等于半径2,
即,解得,
所求直线方程为,或;
(2)直线与圆相交,斜率必定存在,且不为0,设直线方程为,
则圆心到直线的距离,
又∵三角形面积
∴当d=时,S取得最小值2,则,,
故直线方程为y=x-1,或y=7x-7.
点睛:与圆有关的最值问题主要表现在求几何图形的长度、面积的最值,求点到直线的距离的最值,求相关参数的最值等方面.解决此类问题的主要思路是利用圆的几何性质将问题转化.涉及圆中弦长问题,一般利用垂径定理进行解决,具体就是利用半径的平方等于圆心到直线距离平方与弦长一半平方的和
22.(Ⅰ)取BC中点G点,连接AG,FG,F,G分别为DC,BC中点,
得到平面ABC⊥平面BCD,
G为
BC中点,且AC=AB,推出AG⊥BC,从而AG⊥平面BCD,
EF⊥平面BCD.
(Ⅱ)二面角C-DE-A的大小为
【解析】
试题分析:(Ⅰ)取BC中点G点,连接AG,FG,
∵F,G分别为DC,BC中点,
∴FG∥BD且FG=BD,又AE∥BD且AE=BD,
∴AE∥FG且AE=FG,∴四边形EFGA为平行四边形,
∴EF∥AG,∵AE⊥平面ABC,AE∥BD,
BD⊥平面ABC,又∵DB平面BCD,
平面ABC⊥平面BCD,∵G为
BC中点,且AC=AB,
∴AG⊥BC,∴AG⊥平面BCD,
∴EF⊥平面BCD.
6分
(Ⅱ)取AB的中点O和DE的中点H,分别以、、所在直线为x、y、z轴建立如图空间直角坐标系,设,则,,,,,.
设面CDE的法向量,则
取,
8分
取面ABDE的法向量,
10分
由,
故二面角C-DE-A的大小为.
12分
考点:本题主要考查立体几何中的垂直关系、角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。
同课章节目录
