2017—2018学年物理人教版必修1第2章 匀变速直线运动的研究 综合评估
文档属性
| 名称 | 2017—2018学年物理人教版必修1第2章 匀变速直线运动的研究 综合评估 |  | |
| 格式 | zip | ||
| 文件大小 | 579.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-10-12 09:38:17 | ||
图片预览




文档简介
第二章 《匀变速直线运动的研究》综合评估
时间:90分钟 分值:100分
一、选择题(1~6为单选每小题4分,7~10为多选每小题5分,共44分)
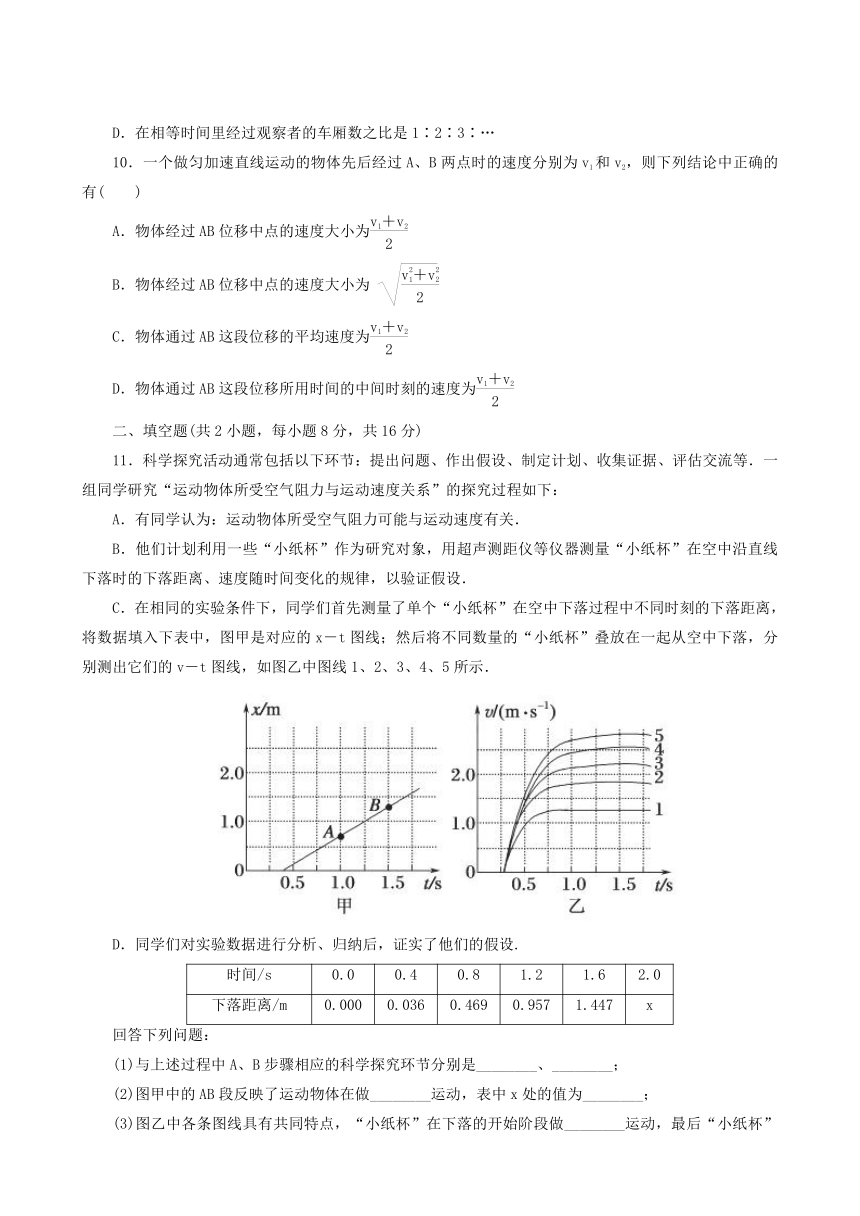
1.
近来,我国大部分地区都出现了雾霾天气,给人们的正常生活造成了极大的影响.在一雾霾天,某人驾驶一辆小汽车以30
m/s的速度行驶在高速公路上,突然发现正前方30
m处有一辆大卡车以10
m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.如图a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
A.因刹车失灵前小汽车已减速,不会追尾
B.在t=5
s时追尾
C.在t=3
s时追尾
D.由于初始距离太近,即使刹车不失灵也会追尾
2.甲、乙两物体在t=0时刻经过同一位置沿x轴运动,其v-t图象如图所示,则( )
A.甲、乙在t=0到t=1
s之间沿同一方向运动
B.乙在t=0到t=7
s之间的位移为零
C.甲在t=0到t=4
s之间做往复运动
D.甲在t=6
s时的加速度为零
3.下图是伽利略1604年做斜面实验时的一页手稿照片,照片左上角的三列数据如下表.表中第二列是时间,第三列是物体沿斜面运动的距离,第一列是伽利略在分析实验数据时添加的.根据表中的数据,伽利略可以得出的结论是( )
1
1
32
4
2
130
9
3
298
16
4
526
25
5
824
36
6
1
192
49
7
1
600
64
8
2
104
A.物体具有惯性
B.斜面倾角一定时,加速度与质量无关
C.物体运动的距离与时间的平方成正比
D.物体运动的加速度与重力加速度成正比
4.一质点沿直线Ox方向做加速运动,它离开O点的距离随时间变化的关系为s=4+2t3(m),它的速度随时间变化的关系为v=6t2(m/s).则该质点在t=2
s时的瞬时速度和t=0到t=2
s间的平均速度分别为( )
A.8
m/s、24
m/s
B.24
m/s、8
m/s
C.24
m/s、10
m/s
D.24
m/s、12
m/s
5.汽车以20
m/s的速度在平直公路上行驶,急刹车时的加速度大小为5
m/s2,则自驾驶员急踩刹车开始,2
s与5
s时汽车的位移之比为( )
A.5∶4
B.4∶5
C.3∶4
D.4∶3
6.四个小球在离地面不同高度同时从静止释放,不计空气阻力,从开始运动时刻起每隔相等的时间间隔,小球依次碰到地面.下列各图中,能反映出刚开始运动时各小球相对面的位置的是( )
7.关于自由落体运动,下列说法正确的是( )
A.它是竖直向下、v0=0、a=g的匀加速直线运动
B.在开始连续的三个1
s内通过的位移之比是1∶3∶5
C.在开始连续的三个1
s末的速度大小之比是1∶2∶3
D.从开始运动起依次下落4.9
m、9.8
m、14.7
m,所经历的时间之比为1∶∶
8.
近两年来,某品牌电梯在北京、上海等地频出事故,为此检修人员对电梯进行检修,检修人员搭乘电梯的v-t图象如图.以下说法正确的是( )
A.6
s末电梯离出发点最远
B.2~4
s电梯做匀速直线运动
C.在4~5
s和5~6
s内电梯的加速度方向相反
D.在4~5
s和5~6
s内电梯的运动方向相反
答案
1.C 根据图象时间轴所围“面积”表示位移的大小,由图知,t=3
s时,大卡车的位移为xb=vbt=10×3
m=30
m,小汽车的位移为xa=×(30+20)×1+×(20+15)×2=60
m,则xa-xb=30
m,所以在t=3
s时追尾,故选项C正确.
2.B 乙在t=0到t=1
s之间做了往返运动,选项A错误;乙在t=0到t=7
s之间的面积为零,位移为零,选项B正确;甲在t=0到t=4
s之间单向直线运动,选项C错误;甲在t=6
s时的速度为零,加速度不为零,选项D错误.
3.C 从表格中的数据可知,时间变为原来的2倍,下滑的位移大约变为原来的4倍,时间变为原来的3倍,位移变为原来的9倍可知,物体运动的距离与时间的平方成正比,故选项C正确.
4.B 将t=2
s代入质点的速度随时间变化的关系式v=6t2(m/s)得,t=2
s瞬时速度为v=6×22
m/s=24
m/s.将t=0
s和t=2
s分别代入距离随时间变化的关系式x=4+2t3(m)得,x1=4
m,x2=20
m,则质点在2
s时间内通过的位移为x=x2-x1=20
m-4
m=16
m,t=0
s到t=2
s间的平均速度为==
m/s=8
m/s;选项B正确.
5.C 汽车刹车到停止所需的时间t0==
s=4
s,2
s时位移x1=v0t-at2=20×2-×5×22
m=30
m,5
s时的位移就是4
s时的位移,此时车已停,x2==
m=40
m,故2
s与5
s时汽车的位移之比为x1∶x2=3∶4,选项C正确.
6.C 依题意可设第1个小球经时间t落地,则第2个小球经时间2t落地,第3个小球经时间3t落地,第4个小球经时间4t落地.又因为四个小球做的都是初速度为零的匀加速运动,因此它们下落的高度之比为1
∶4∶9∶16,只有C正确.
7.ABC 自由落体运动为初速度为零的匀加速直线运动,加速度为g,所以A对;第一个1
s内的位移x1=gt,第二个1
s内的位移x2=g(2t0)2-gt=gt,第三个1
s内的位移x3=g(3t0)2-g(2t0)2=gt,则x1∶x2∶x3=1∶3∶5,所以B对;第1
s末的速度v1=gt0,第2
s末的速度v2=2gt0,第3
s末的速度v3=3gt0,则v1∶v2∶v3=1∶2∶3,所以C对;通过4.9
m的时间t1=
s再下落9.8
m的时间t2=
s-
s,再下落14.7
m的时间t3=
s-
s,则t1∶t2∶t3=1∶(-1)∶(-),所以D不对.
8.BD 图象的“面积”等于位移大小,由图看出,5
s末位移最大,故选项A错误;在2~4秒内图象的斜率为零,说明电梯做匀速直线运动,故选项B正确;在4~6
s内,速度图象是一条直线,其斜率保持不变,说明加速度保持不变,故选项C错误;在4~5
s内速度为正,在5~6
s内速度为负,说明电梯的运动方向相反,故选项D正确.
———————————————————————————
9.一观察者站在第一节车厢前端的旁边,当列车从静止开始做匀加速运动时( )
A.每节车厢末端经过观察者的速度之比是1∶∶∶…∶
B.每节车厢末端经过观察者的时间之比是1∶3∶5∶…∶n
C.在相等时间里经过观察者的车厢数之比是1∶3∶5∶…
D.在相等时间里经过观察者的车厢数之比是1∶2∶3∶…
10.一个做匀加速直线运动的物体先后经过A、B两点时的速度分别为v1和v2,则下列结论中正确的有( )
A.物体经过AB位移中点的速度大小为
B.物体经过AB位移中点的速度大小为
C.物体通过AB这段位移的平均速度为
D.物体通过AB这段位移所用时间的中间时刻的速度为
二、填空题(共2小题,每小题8分,共16分)
11.科学探究活动通常包括以下环节:提出问题、作出假设、制定计划、收集证据、评估交流等.一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下:
A.有同学认为:运动物体所受空气阻力可能与运动速度有关.
B.他们计划利用一些“小纸杯”作为研究对象,用超声测距仪等仪器测量“小纸杯”在空中沿直线下落时的下落距离、速度随时间变化的规律,以验证假设.
C.在相同的实验条件下,同学们首先测量了单个“小纸杯”在空中下落过程中不同时刻的下落距离,将数据填入下表中,图甲是对应的x-t图线;然后将不同数量的“小纸杯”叠放在一起从空中下落,分别测出它们的v-t图线,如图乙中图线1、2、3、4、5所示.
D.同学们对实验数据进行分析、归纳后,证实了他们的假设.
时间/s
0.0
0.4
0.8
1.2
1.6
2.0
下落距离/m
0.000
0.036
0.469
0.957
1.447
x
回答下列问题:
(1)与上述过程中A、B步骤相应的科学探究环节分别是________、________;
(2)图甲中的AB段反映了运动物体在做________运动,表中x处的值为________;
(3)图乙中各条图线具有共同特点,“小纸杯”在下落的开始阶段做________运动,最后“小纸杯”做________运动;
(4)比较图乙中的图线1和5,指出在1.0~1.5
s内,速度随时间变化关系的差异.
12.
利用如图所示的装置可测量滑块在斜面上运动的加速度.一斜面上安装有两个光电门,其中光电门乙固定在斜面上靠近底端处,光电门甲的位置可移动.当一带有遮光片的滑块自斜面上滑下时,与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间t.改变光电门甲的位置进行多次测量,每次都使滑块从同一点由静止开始下滑,并用刻度尺测量甲、乙之间的距离x,记下相应的t值;所得数据如下表所示.
x/m
0.500
0.600
0.700
0.800
0.900
0.950
t/ms
292.9
371.5
452.3
552.8
673.8
776.4
x/t(m·s-1)
1.71
1.62
1.55
1.45
1.34
1.22
完成下列填空和作图:
(1)若滑块所受摩擦力为一常量,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度vt、测量值x和t四个物理量之间所满足的关系式是________;
(2)根据表中给出的数据,在下图给出的坐标纸上画出-t图线;
(3)由所画出的-t图线,得出滑块加速度的大小为a=________m/s2(保留2位有效数字).
答案
9.AC 由v2=2ax可知:v=2ax,v=2a·2x,v=2a·3x,…,v=2a·nx,
所以v1∶v2∶v3∶…∶vn=1∶∶∶…∶,A正确.
由x=at2知:t=,t=,
t=…t=,
所以t1∶t2∶t3∶…∶tn=1∶∶∶…∶,B错.
由相同时间通过位移比例可知,C正确,D错.
10.BCD 设经过位移中点时的速度为v
eq
\s\do8()
,则对前半段的位移有2a·=v2
eq
\s\do8()
-v,对后半段的位移有2a·=v-v2
eq
\s\do8()
,由这两式得v
eq
\s\do8()
=,选项A错误,选项B正确;对匀变速直线运动而言,总有=v=,选项C、D正确.
11.(1)作出假设 制定计划
(2)匀速直线 1.937
m
(3)加速度减小的加速直线 匀速直线
(4)见解析
解析:(1)A、B步骤相应的环节分别是作出假设和制定计划.
(2)从图甲可以看出,AB段是向上倾斜的直线,
所以是匀速直线运动.
由于从1.2~1.6
s和1.6~2.0
s两个时间段相等(都是0.4
s)
故两段下落的高度相等,则
x=[1.447+(1.447-0.957)]m=1.937
m.
(3)从图乙可以看出,“小纸杯”在开始阶段加速度逐渐减小,最后减为0,故开始先做加速度减小的加速直线运动,最后做匀速直线运动.
(4)由图乙可以看出,在1.0~1.5
s内,图线1反映速度不随时间而变化(或图线1反映纸杯做匀速直线运动),图线5反映速度随时间继续增大(或图线5反映纸杯依然在做加速度逐渐减小的加速直线运动).
12.(1)=-at+vt(或写成x=-at2+vtt也可)
(2)-t图线如图所示
(3)2.0(答案在1.8~2.2范围内都可)
解析:沿斜面向下是匀加速运动,反过来也可以看成是初速度为vt的沿斜面向上的匀减速运动,由位移公式有x=vtt-at2.由于要画-t图象,所以可将上式变形得=-t+vt,可知图象的斜率k=-,a=-2k,求出a值.
———————————————————————————
三、计算题(共4小题,每小题10分)
13.从足够高处先后让两个钢球自由下落,两球间用长为9.8
m的细绳连接.第一个球下落1
s后第二个球开始下落.不计空气阻力及绳的质量,试求在第二个球开始下落后多长时间,连接两球的细绳刚好被拉直?(g取9.8
m/s2).
14.甲、乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变.在第一段时间间隔内,两辆汽车的加速度大小不变,汽车乙的加速度大小是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的加速度大小减小为原来的一半.求甲、乙两车各自在这两段时间间隔内走过的总路程之比.
答案
13.0.5
s
解析:设第二个球开始下落后经时间t连接两球的细绳刚好被拉直
对第一个球:h1=g(t+Δt)2
对第二个球:h2=gt2
细绳刚好被拉直时有:h1=h2+L
由以上三式解得:t=0.5
s.
14.
解析:设汽车甲在第一段时间间隔末(时刻t0)的速度为v,第一段时间间隔内行驶的路程为s1,加速度为a;在第二段时间间隔内行驶的路程为s2.由运动学公式得:v=at0,s1=at,s2=vt0+(2a)t.
设汽车乙在时刻t0的速度为v′,在第一、二段时间间隔内行驶的路程分别为s′1、s′2.同样有:v′=(2a)t0,s′1=(2a)t,s′2=v′t0+at,设甲、乙两车行驶的总路程分别为s、s′,则有:s=s1+s2,s′=s′1+s′2,联立以上各式解得,甲、乙两车各自行驶的总路程之比为=.
———————————————————————————
15.汽车一般有五个前进挡位,对应不同的速度范围,设在每一挡汽车均做匀变速直线运动,换挡时间不计.某次行车时,一挡起步,起步后马上挂入二挡,加速度为2
m/s2,3
s后挂入三挡,再经过4
s速度达到13
m/s,随即挂入四挡,加速度为1.5
m/s2,速度达到16
m/s时挂上五挡,加速度为1
m/s2.求:
(1)汽车在三挡时的加速度大小;
(2)汽车在四挡行驶的时间;
(3)汽车挂上五挡后再过5
s的速度大小.
16.汽车启动的快慢和能够达到的最大速度,是衡量汽车性能指标体系中的两个重要指标.汽车启动的快慢用车的速度从0到100
km/h的加速时间来表示,这个时间越短,汽车启动时的加速度就越大.下表中列出了两种汽车的性能指标(为了简化计算,把100
km/h取为30
m/s).
启动的快慢/s(0
m/s~30
m/s的加速时间)
最大速度/(m·s-1)
甲车
12
40
乙车
6
50
现在,甲、乙两车在同一条平直公路上,车头向着同一个方向,乙车在前,甲车在后,两车相距85
m.甲车先启动,经过一段时间t0乙车再启动.若两车从速度为0到最大速度的时间内都以最大加速度做匀加速直线运动,在乙车开出8
s时两车相遇,则:
(1)t0应满足的条件是什么?
(2)在此条件下,两车相遇时甲车行驶的路程是多少?
答案
15.(1)1.75
m/s2 (2)2
s (3)21
m/s
解析:(1)汽车的运动过程草图如图所示.
在二挡时(A→B),a1=2
m/s2,t1=3
s,这一过程的末速度v1=a1t1=2×3
m/s=6
m/s
在三挡时(B→C),v2=13
m/s,t2=4
s
加速度a2==
m/s2=1.75
m/s2
即汽车在三挡时的加速度大小为1.75
m/s2.
(2)在四挡时(C→D),a3=1.5
m/s2
v3=16
m/s,运动时间
t3==
s=2
s
即汽车在四挡行驶的时间为2
s.
(3)在五挡时(D→E),a4=1
m/s2,t4=5
s
速度v4=v3+a4t4=16
m/s+1×5
m/s=21
m/s
故汽车挂上五挡后再过5
s的速度大小为21
m/s.
16.(1)6
s
(2)两次相遇,t=4
s和t=8
s,甲车路程分别是125
m和245
m
解析:(1)设甲车匀加速运动阶段的加速度为a1,最大速度为v1m,位移为x1,加速时间为t1,乙车匀加速运动阶段的加速度为a2,最大速度为v2m,位移为x2,加速时间为t2,由题意得:a=,x=at2=t.a1=m/s2=2.5
m/s2,a2=
m/s2=5
m/s2.t1==16
s,t2==10
s,x1=320
m,x2=250
m.
设乙车开出8
s后,位移为x′2,则x′2=a2t′=160
m.160
m+85
m=245
m<320
m,故甲、乙两车相遇时甲车在匀加速运动阶段.由甲、乙两车的位移关系有x甲=x乙+85
m,则a1(t0+8)2=160
m+85
m,解之得t0=6
s.
(2)分析知甲、乙两车有两次相遇的情况.
设甲、乙两车相遇时乙车行驶的时间为t,
则有a1(t+t0)2=a2t2+85.
解得t=4
s或t=8
s.
第一次相遇:x甲=a1(4+t0)2=125
m,
第二次相遇:x甲=a1(8+t0)2=245
m.
当第二次相遇时,v1=35
m/s,v2=40
m/s.
v2>v1,故之后甲、乙不再相遇.
时间:90分钟 分值:100分
一、选择题(1~6为单选每小题4分,7~10为多选每小题5分,共44分)
1.
近来,我国大部分地区都出现了雾霾天气,给人们的正常生活造成了极大的影响.在一雾霾天,某人驾驶一辆小汽车以30
m/s的速度行驶在高速公路上,突然发现正前方30
m处有一辆大卡车以10
m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.如图a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
A.因刹车失灵前小汽车已减速,不会追尾
B.在t=5
s时追尾
C.在t=3
s时追尾
D.由于初始距离太近,即使刹车不失灵也会追尾
2.甲、乙两物体在t=0时刻经过同一位置沿x轴运动,其v-t图象如图所示,则( )
A.甲、乙在t=0到t=1
s之间沿同一方向运动
B.乙在t=0到t=7
s之间的位移为零
C.甲在t=0到t=4
s之间做往复运动
D.甲在t=6
s时的加速度为零
3.下图是伽利略1604年做斜面实验时的一页手稿照片,照片左上角的三列数据如下表.表中第二列是时间,第三列是物体沿斜面运动的距离,第一列是伽利略在分析实验数据时添加的.根据表中的数据,伽利略可以得出的结论是( )
1
1
32
4
2
130
9
3
298
16
4
526
25
5
824
36
6
1
192
49
7
1
600
64
8
2
104
A.物体具有惯性
B.斜面倾角一定时,加速度与质量无关
C.物体运动的距离与时间的平方成正比
D.物体运动的加速度与重力加速度成正比
4.一质点沿直线Ox方向做加速运动,它离开O点的距离随时间变化的关系为s=4+2t3(m),它的速度随时间变化的关系为v=6t2(m/s).则该质点在t=2
s时的瞬时速度和t=0到t=2
s间的平均速度分别为( )
A.8
m/s、24
m/s
B.24
m/s、8
m/s
C.24
m/s、10
m/s
D.24
m/s、12
m/s
5.汽车以20
m/s的速度在平直公路上行驶,急刹车时的加速度大小为5
m/s2,则自驾驶员急踩刹车开始,2
s与5
s时汽车的位移之比为( )
A.5∶4
B.4∶5
C.3∶4
D.4∶3
6.四个小球在离地面不同高度同时从静止释放,不计空气阻力,从开始运动时刻起每隔相等的时间间隔,小球依次碰到地面.下列各图中,能反映出刚开始运动时各小球相对面的位置的是( )
7.关于自由落体运动,下列说法正确的是( )
A.它是竖直向下、v0=0、a=g的匀加速直线运动
B.在开始连续的三个1
s内通过的位移之比是1∶3∶5
C.在开始连续的三个1
s末的速度大小之比是1∶2∶3
D.从开始运动起依次下落4.9
m、9.8
m、14.7
m,所经历的时间之比为1∶∶
8.
近两年来,某品牌电梯在北京、上海等地频出事故,为此检修人员对电梯进行检修,检修人员搭乘电梯的v-t图象如图.以下说法正确的是( )
A.6
s末电梯离出发点最远
B.2~4
s电梯做匀速直线运动
C.在4~5
s和5~6
s内电梯的加速度方向相反
D.在4~5
s和5~6
s内电梯的运动方向相反
答案
1.C 根据图象时间轴所围“面积”表示位移的大小,由图知,t=3
s时,大卡车的位移为xb=vbt=10×3
m=30
m,小汽车的位移为xa=×(30+20)×1+×(20+15)×2=60
m,则xa-xb=30
m,所以在t=3
s时追尾,故选项C正确.
2.B 乙在t=0到t=1
s之间做了往返运动,选项A错误;乙在t=0到t=7
s之间的面积为零,位移为零,选项B正确;甲在t=0到t=4
s之间单向直线运动,选项C错误;甲在t=6
s时的速度为零,加速度不为零,选项D错误.
3.C 从表格中的数据可知,时间变为原来的2倍,下滑的位移大约变为原来的4倍,时间变为原来的3倍,位移变为原来的9倍可知,物体运动的距离与时间的平方成正比,故选项C正确.
4.B 将t=2
s代入质点的速度随时间变化的关系式v=6t2(m/s)得,t=2
s瞬时速度为v=6×22
m/s=24
m/s.将t=0
s和t=2
s分别代入距离随时间变化的关系式x=4+2t3(m)得,x1=4
m,x2=20
m,则质点在2
s时间内通过的位移为x=x2-x1=20
m-4
m=16
m,t=0
s到t=2
s间的平均速度为==
m/s=8
m/s;选项B正确.
5.C 汽车刹车到停止所需的时间t0==
s=4
s,2
s时位移x1=v0t-at2=20×2-×5×22
m=30
m,5
s时的位移就是4
s时的位移,此时车已停,x2==
m=40
m,故2
s与5
s时汽车的位移之比为x1∶x2=3∶4,选项C正确.
6.C 依题意可设第1个小球经时间t落地,则第2个小球经时间2t落地,第3个小球经时间3t落地,第4个小球经时间4t落地.又因为四个小球做的都是初速度为零的匀加速运动,因此它们下落的高度之比为1
∶4∶9∶16,只有C正确.
7.ABC 自由落体运动为初速度为零的匀加速直线运动,加速度为g,所以A对;第一个1
s内的位移x1=gt,第二个1
s内的位移x2=g(2t0)2-gt=gt,第三个1
s内的位移x3=g(3t0)2-g(2t0)2=gt,则x1∶x2∶x3=1∶3∶5,所以B对;第1
s末的速度v1=gt0,第2
s末的速度v2=2gt0,第3
s末的速度v3=3gt0,则v1∶v2∶v3=1∶2∶3,所以C对;通过4.9
m的时间t1=
s再下落9.8
m的时间t2=
s-
s,再下落14.7
m的时间t3=
s-
s,则t1∶t2∶t3=1∶(-1)∶(-),所以D不对.
8.BD 图象的“面积”等于位移大小,由图看出,5
s末位移最大,故选项A错误;在2~4秒内图象的斜率为零,说明电梯做匀速直线运动,故选项B正确;在4~6
s内,速度图象是一条直线,其斜率保持不变,说明加速度保持不变,故选项C错误;在4~5
s内速度为正,在5~6
s内速度为负,说明电梯的运动方向相反,故选项D正确.
———————————————————————————
9.一观察者站在第一节车厢前端的旁边,当列车从静止开始做匀加速运动时( )
A.每节车厢末端经过观察者的速度之比是1∶∶∶…∶
B.每节车厢末端经过观察者的时间之比是1∶3∶5∶…∶n
C.在相等时间里经过观察者的车厢数之比是1∶3∶5∶…
D.在相等时间里经过观察者的车厢数之比是1∶2∶3∶…
10.一个做匀加速直线运动的物体先后经过A、B两点时的速度分别为v1和v2,则下列结论中正确的有( )
A.物体经过AB位移中点的速度大小为
B.物体经过AB位移中点的速度大小为
C.物体通过AB这段位移的平均速度为
D.物体通过AB这段位移所用时间的中间时刻的速度为
二、填空题(共2小题,每小题8分,共16分)
11.科学探究活动通常包括以下环节:提出问题、作出假设、制定计划、收集证据、评估交流等.一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下:
A.有同学认为:运动物体所受空气阻力可能与运动速度有关.
B.他们计划利用一些“小纸杯”作为研究对象,用超声测距仪等仪器测量“小纸杯”在空中沿直线下落时的下落距离、速度随时间变化的规律,以验证假设.
C.在相同的实验条件下,同学们首先测量了单个“小纸杯”在空中下落过程中不同时刻的下落距离,将数据填入下表中,图甲是对应的x-t图线;然后将不同数量的“小纸杯”叠放在一起从空中下落,分别测出它们的v-t图线,如图乙中图线1、2、3、4、5所示.
D.同学们对实验数据进行分析、归纳后,证实了他们的假设.
时间/s
0.0
0.4
0.8
1.2
1.6
2.0
下落距离/m
0.000
0.036
0.469
0.957
1.447
x
回答下列问题:
(1)与上述过程中A、B步骤相应的科学探究环节分别是________、________;
(2)图甲中的AB段反映了运动物体在做________运动,表中x处的值为________;
(3)图乙中各条图线具有共同特点,“小纸杯”在下落的开始阶段做________运动,最后“小纸杯”做________运动;
(4)比较图乙中的图线1和5,指出在1.0~1.5
s内,速度随时间变化关系的差异.
12.
利用如图所示的装置可测量滑块在斜面上运动的加速度.一斜面上安装有两个光电门,其中光电门乙固定在斜面上靠近底端处,光电门甲的位置可移动.当一带有遮光片的滑块自斜面上滑下时,与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间t.改变光电门甲的位置进行多次测量,每次都使滑块从同一点由静止开始下滑,并用刻度尺测量甲、乙之间的距离x,记下相应的t值;所得数据如下表所示.
x/m
0.500
0.600
0.700
0.800
0.900
0.950
t/ms
292.9
371.5
452.3
552.8
673.8
776.4
x/t(m·s-1)
1.71
1.62
1.55
1.45
1.34
1.22
完成下列填空和作图:
(1)若滑块所受摩擦力为一常量,滑块加速度的大小a、滑块经过光电门乙时的瞬时速度vt、测量值x和t四个物理量之间所满足的关系式是________;
(2)根据表中给出的数据,在下图给出的坐标纸上画出-t图线;
(3)由所画出的-t图线,得出滑块加速度的大小为a=________m/s2(保留2位有效数字).
答案
9.AC 由v2=2ax可知:v=2ax,v=2a·2x,v=2a·3x,…,v=2a·nx,
所以v1∶v2∶v3∶…∶vn=1∶∶∶…∶,A正确.
由x=at2知:t=,t=,
t=…t=,
所以t1∶t2∶t3∶…∶tn=1∶∶∶…∶,B错.
由相同时间通过位移比例可知,C正确,D错.
10.BCD 设经过位移中点时的速度为v
eq
\s\do8()
,则对前半段的位移有2a·=v2
eq
\s\do8()
-v,对后半段的位移有2a·=v-v2
eq
\s\do8()
,由这两式得v
eq
\s\do8()
=,选项A错误,选项B正确;对匀变速直线运动而言,总有=v=,选项C、D正确.
11.(1)作出假设 制定计划
(2)匀速直线 1.937
m
(3)加速度减小的加速直线 匀速直线
(4)见解析
解析:(1)A、B步骤相应的环节分别是作出假设和制定计划.
(2)从图甲可以看出,AB段是向上倾斜的直线,
所以是匀速直线运动.
由于从1.2~1.6
s和1.6~2.0
s两个时间段相等(都是0.4
s)
故两段下落的高度相等,则
x=[1.447+(1.447-0.957)]m=1.937
m.
(3)从图乙可以看出,“小纸杯”在开始阶段加速度逐渐减小,最后减为0,故开始先做加速度减小的加速直线运动,最后做匀速直线运动.
(4)由图乙可以看出,在1.0~1.5
s内,图线1反映速度不随时间而变化(或图线1反映纸杯做匀速直线运动),图线5反映速度随时间继续增大(或图线5反映纸杯依然在做加速度逐渐减小的加速直线运动).
12.(1)=-at+vt(或写成x=-at2+vtt也可)
(2)-t图线如图所示
(3)2.0(答案在1.8~2.2范围内都可)
解析:沿斜面向下是匀加速运动,反过来也可以看成是初速度为vt的沿斜面向上的匀减速运动,由位移公式有x=vtt-at2.由于要画-t图象,所以可将上式变形得=-t+vt,可知图象的斜率k=-,a=-2k,求出a值.
———————————————————————————
三、计算题(共4小题,每小题10分)
13.从足够高处先后让两个钢球自由下落,两球间用长为9.8
m的细绳连接.第一个球下落1
s后第二个球开始下落.不计空气阻力及绳的质量,试求在第二个球开始下落后多长时间,连接两球的细绳刚好被拉直?(g取9.8
m/s2).
14.甲、乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变.在第一段时间间隔内,两辆汽车的加速度大小不变,汽车乙的加速度大小是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的加速度大小减小为原来的一半.求甲、乙两车各自在这两段时间间隔内走过的总路程之比.
答案
13.0.5
s
解析:设第二个球开始下落后经时间t连接两球的细绳刚好被拉直
对第一个球:h1=g(t+Δt)2
对第二个球:h2=gt2
细绳刚好被拉直时有:h1=h2+L
由以上三式解得:t=0.5
s.
14.
解析:设汽车甲在第一段时间间隔末(时刻t0)的速度为v,第一段时间间隔内行驶的路程为s1,加速度为a;在第二段时间间隔内行驶的路程为s2.由运动学公式得:v=at0,s1=at,s2=vt0+(2a)t.
设汽车乙在时刻t0的速度为v′,在第一、二段时间间隔内行驶的路程分别为s′1、s′2.同样有:v′=(2a)t0,s′1=(2a)t,s′2=v′t0+at,设甲、乙两车行驶的总路程分别为s、s′,则有:s=s1+s2,s′=s′1+s′2,联立以上各式解得,甲、乙两车各自行驶的总路程之比为=.
———————————————————————————
15.汽车一般有五个前进挡位,对应不同的速度范围,设在每一挡汽车均做匀变速直线运动,换挡时间不计.某次行车时,一挡起步,起步后马上挂入二挡,加速度为2
m/s2,3
s后挂入三挡,再经过4
s速度达到13
m/s,随即挂入四挡,加速度为1.5
m/s2,速度达到16
m/s时挂上五挡,加速度为1
m/s2.求:
(1)汽车在三挡时的加速度大小;
(2)汽车在四挡行驶的时间;
(3)汽车挂上五挡后再过5
s的速度大小.
16.汽车启动的快慢和能够达到的最大速度,是衡量汽车性能指标体系中的两个重要指标.汽车启动的快慢用车的速度从0到100
km/h的加速时间来表示,这个时间越短,汽车启动时的加速度就越大.下表中列出了两种汽车的性能指标(为了简化计算,把100
km/h取为30
m/s).
启动的快慢/s(0
m/s~30
m/s的加速时间)
最大速度/(m·s-1)
甲车
12
40
乙车
6
50
现在,甲、乙两车在同一条平直公路上,车头向着同一个方向,乙车在前,甲车在后,两车相距85
m.甲车先启动,经过一段时间t0乙车再启动.若两车从速度为0到最大速度的时间内都以最大加速度做匀加速直线运动,在乙车开出8
s时两车相遇,则:
(1)t0应满足的条件是什么?
(2)在此条件下,两车相遇时甲车行驶的路程是多少?
答案
15.(1)1.75
m/s2 (2)2
s (3)21
m/s
解析:(1)汽车的运动过程草图如图所示.
在二挡时(A→B),a1=2
m/s2,t1=3
s,这一过程的末速度v1=a1t1=2×3
m/s=6
m/s
在三挡时(B→C),v2=13
m/s,t2=4
s
加速度a2==
m/s2=1.75
m/s2
即汽车在三挡时的加速度大小为1.75
m/s2.
(2)在四挡时(C→D),a3=1.5
m/s2
v3=16
m/s,运动时间
t3==
s=2
s
即汽车在四挡行驶的时间为2
s.
(3)在五挡时(D→E),a4=1
m/s2,t4=5
s
速度v4=v3+a4t4=16
m/s+1×5
m/s=21
m/s
故汽车挂上五挡后再过5
s的速度大小为21
m/s.
16.(1)6
s
(2)两次相遇,t=4
s和t=8
s,甲车路程分别是125
m和245
m
解析:(1)设甲车匀加速运动阶段的加速度为a1,最大速度为v1m,位移为x1,加速时间为t1,乙车匀加速运动阶段的加速度为a2,最大速度为v2m,位移为x2,加速时间为t2,由题意得:a=,x=at2=t.a1=m/s2=2.5
m/s2,a2=
m/s2=5
m/s2.t1==16
s,t2==10
s,x1=320
m,x2=250
m.
设乙车开出8
s后,位移为x′2,则x′2=a2t′=160
m.160
m+85
m=245
m<320
m,故甲、乙两车相遇时甲车在匀加速运动阶段.由甲、乙两车的位移关系有x甲=x乙+85
m,则a1(t0+8)2=160
m+85
m,解之得t0=6
s.
(2)分析知甲、乙两车有两次相遇的情况.
设甲、乙两车相遇时乙车行驶的时间为t,
则有a1(t+t0)2=a2t2+85.
解得t=4
s或t=8
s.
第一次相遇:x甲=a1(4+t0)2=125
m,
第二次相遇:x甲=a1(8+t0)2=245
m.
当第二次相遇时,v1=35
m/s,v2=40
m/s.
v2>v1,故之后甲、乙不再相遇.
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
