11.3 多边形及其内角和培优提高试题
文档属性
| 名称 | 11.3 多边形及其内角和培优提高试题 |  | |
| 格式 | doc | ||
| 文件大小 | 614.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-12 11:19:08 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
八上数学第十一章培优提高 多边形培优测试
一.选择题(共11小题)
1.如图,已知在△ABC中,AD是∠BAC的角平分线,AE是BC边上的高,且∠B=25°,∠C=55°,则∠DAE的度数是( )21世纪教育网版权所有
A.15° B.35° C.65° D.75°
2.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A.27 B.35 C.44 D.54
3.如图,BD,CE分别是△ABC的两条高、它们相交于点H,那么下列式子中正确的有( )个.(1)∠DHC=∠A;(2)∠EBH+∠A=90°;(3)∠ACE=∠ABD;(4)∠ECB=∠ABC.
A.1 B.2 C.3 D.4
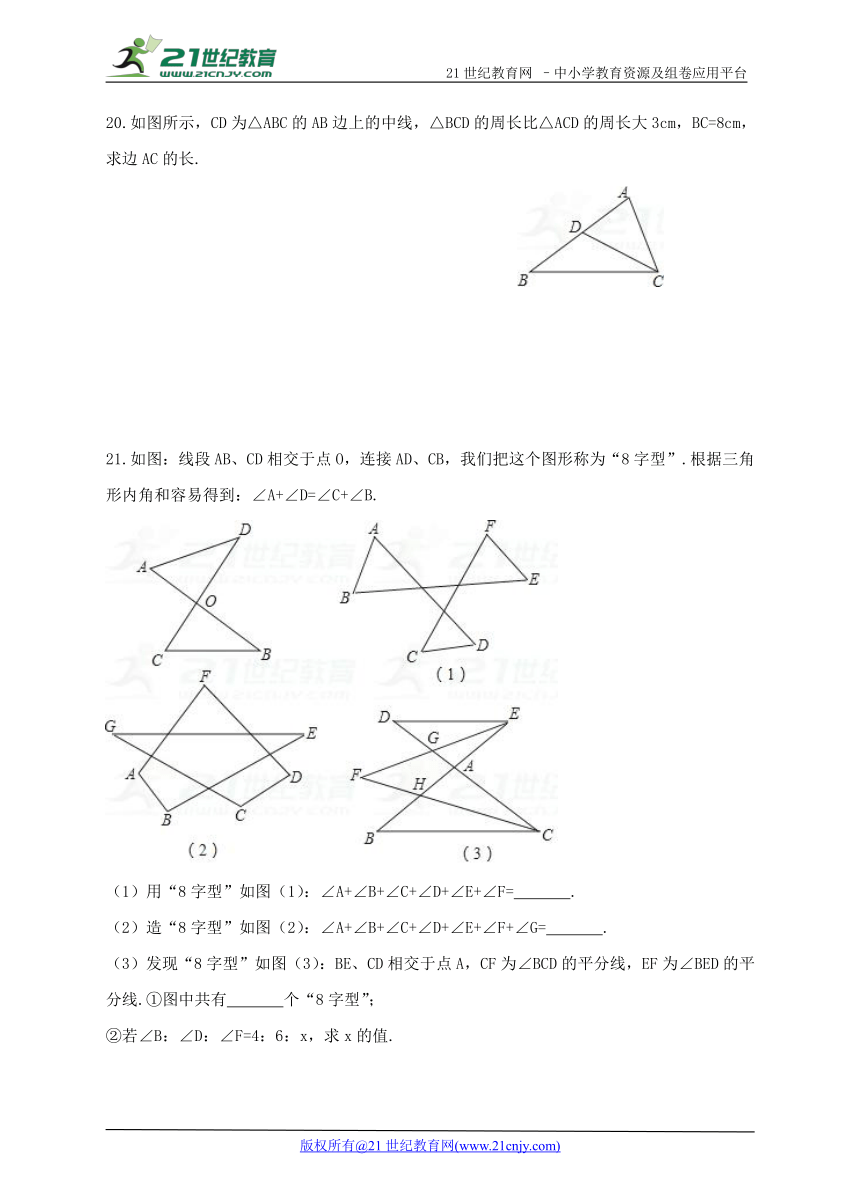
4.如图所示,∠A+∠B+∠C+∠D+∠E+∠F等于( )
A.180° B.270° C.360° D.540°
第1题图 第3题图 第4题图
5.在美化泸州的建设中,常用正多边形的瓷砖铺地面,在①正三角形、②正方形、③正五边形、④正六边形、⑤正七边形中,如果限于用一种正多边形进行平面镶嵌,能单独镶嵌成一个平面的正多边形有( )21教育网
A.①②③ B.②③④ C.③④⑤ D.①②④
6.多边形的边数增加1时、它的内角和与外角和( )
A.都不变 B.内角和增加180°外角和不变
C.都增加180° D.内角和增加180°外角和减少180°
7.下列命题中,①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360°;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤一个三角形中至少有两个锐角;⑥在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形,其中假命题是( )21cnjy.com
A.①②③④ B.②④⑥ C.②③⑤ D.①②③④⑥
8.一个三角形的两边分别是4和9,而第三边的长为奇数,则第三边的长是( )
A.3或5或7 B.9或11或13 C.5或7或9 D.7或9或11
9.用正三角形和正六边形镶嵌,若每一个顶点周围有m个正三角形、n个正六边形,则m,n满足的关系式是( )【来源:21·世纪·教育·网】
A.2m+3n=12 B.m+n=8 C.2m+n=6 D.m+2n=6
10.在一个n边形中,除了一个内角外,其余(n﹣1)个内角和为2750°,则这个内角是( )
A.140° B.105° C.120° D.130°
第11题图 第12题图 第14题
二.填空题(共8小题)
11.如图,∠1、∠2是△ABC的外角,已知∠1+∠2=260°,求∠A的度数是 .
12.如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3= .21·世纪*教育网
13.一个等腰三角形的两边长分别是4cm和7cm,且它的周长大于16cm,则第三边是 .
14.如图,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠BDE= .【出处:21教育名师】
第16题 第17题
15.在△ABC中,∠A=90°,∠B﹣∠C=24°,那么∠B= 度,∠C= 度.
16.如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F在AD上,若△ABC的面积为16cm2,则图中阴影部分的面积为 cm2.21教育名师原创作品
17.如图中每个阴影部分是以多边形各顶点为圆心,2为半径的扇形,并且所有多边形的每条边长都大于2,则第n个多边形中,所有扇形面积之和是 (结果保留π).
18.如图,G是△AFE两外角平分线的交点,P是△ABC的两外角平分线的交点,F,C在AN上,又B,E在AM上;如果∠FGE=66°,那么∠P= 度.21*cnjy*com
第20题图
一.解答题(共5小题)
19.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
20.如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.www.21-cn-jy.com
21.如图:线段AB、CD相交于点O,连接AD、CB,我们把这个图形称为“8字型”.根据三角形内角和容易得到:∠A+∠D=∠C+∠B.【来源:21cnj*y.co*m】
(1)用“8字型”如图(1):∠A+∠B+∠C+∠D+∠E+∠F= .
(2)造“8字型”如图(2):∠A+∠B+∠C+∠D+∠E+∠F+∠G= .
(3)发现“8字型”如图(3):BE、CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.①图中共有 个“8字型”;【版权所有:21教育】
②若∠B:∠D:∠F=4:6:x,求x的值.
22.如图,将一块直角三角尺DEF放置在锐角三角形ABC上,使得该三角尺的两条直角边DE,DF恰好分别经过点B,C.
(1)如图①,点D在△ABC内.
(i)若∠A=40°,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;2·1·c·n·j·y
(ii)请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
23.如图1的图形,像我们常见的风筝.我们不妨把这样图形叫做“筝形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?
下面就请你发挥你的聪明才智,解决以下问题:
观察“筝形”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=58°,则∠ABX+∠ACX= °;www-2-1-cnjy-com
②如图3,已知DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=150°,则∠DCE= °;
②如图4,已知∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠B G1C=77°,则∠A= °.
参考答案
一.选择题(共11小题)
1A.【解答】解:∵△ABC中,∠B=25°,∠C=55°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣25°﹣55°=100°,∵AD是∠BAC的平分线,∴∠DAC=∠BAC=50°,∵AE是BC边上的高,在直角△AEC中,∵∠EAC=90°﹣∠C=90°﹣55°=35°,∴∠DAE=∠DAC﹣∠EAC=50°﹣35°=15°.故选:A.2-1-c-n-j-y
2C.【解答】解:设这个内角度数为x°,边数为n,∴(n﹣2)×180﹣x=1510,
180n=1870+x=1800+(70+x),∵n为正整数,∴n=11,∴=44,
3C.【解答】解:△ABC的高BD、CE相交于点H,(1)在四边形AEHD中,∠AED+∠ADH=∠A+∠DHE=∠DHE+DHC=180°,所以∠DHC=∠A,(1)正确;
(2)因为∠EHB=∠DHC=∠A,所以∠EBH+∠A=∠EBH+∠A=90°,故(2)正确;
(3)∠ABD+∠A=90°,∠ACE+∠A=90°,∴∠ABD=∠ACE,故(3)正确;
(4)∠ECB+∠ABC=90°,但∠ECB=∠ABC不正确,故(4)错误;
4C.【解答】解:∵∠A+∠F=180°﹣∠AOF,∠B+∠C=180°﹣∠BNC,
∠E+∠D=180°﹣∠DME,又∵∠AOF=∠NOM(对顶角相等),
∠BNC=∠ONM(对顶角相等),∠DME=∠NMO(对顶角相等),
又∵∠NOM+∠ONM+∠NMO=180°(三角形内角和等于180°),
∴∠A+∠B+∠C+∠D+∠E+∠F=180°﹣∠AOF+180°﹣∠BNC+180°﹣∠DME,
=540°﹣(∠NOM+∠ONM+∠NMO),=540°﹣180°,=360°.故选C.
5D.【解答】解:①正三角形每个内角是60°,能被360°整除,所以能单独镶嵌成一个平面;
②正方形每个内角是90°,能被360°整除,所以能单独镶嵌成一个平面;
③正五边形每个内角是108°,不能被360°整除,所以不能单独镶嵌成一个平面;
④正六边形每个内角是120°,能被360°整除,所以能单独镶嵌成一个平面;
⑤正七边形每个内角的度数不能被360°整除,所以不能单独镶嵌成一个平面.
故能单独镶嵌成一个平面的正多边形有:①②④.故选D.
6B.【解答】解:根据n边形的内角和可以表示成(n﹣2) 180°,
可以得到增加一条边时,边数变为n+1,
则内角和是(n﹣1) 180°,因而内角和增加:(n﹣1) 180°﹣(n﹣2) 180°=180°.
多边形外角和为360°,故选B.
7D.【解答】解:①错误.直角三角形的三条高(或高的延长线)的交点在直角顶点处.
②错误.应该是一个多边形的边数每增加一条,这个多边形的内角和就增加180°.
③错误.应该是两条平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
④错误.应该是三角形的一个外角等于不相邻的两个内角的和.
⑤正确.一个三角形中至少有两个锐角.
⑥错误.设∠A=6x,则∠B=3x,∠C=2x,由题意6x+3x+2x=180,解得x=()°,∴∠A、∠B、∠C中没有直角,∴△ABC表示直角三角形.故选D.
8D.【解答】解:根据题意得:5<第三边<13,又∵第三边的长为奇数,
∴第三边的长是7,9,11.故选D.
9D.【解答】解:正多边形的平面镶嵌,每一个顶点处的几个角之和应为360度,
而正三角形和正六边形内角分别为60°、120°,根据题意可知60°×m+120°×n=360°,化简得到m+2n=6.故选D.21·cn·jy·com
10D.【解答】解:多边形内角和(n﹣2)×180°,则多边形内角和一定是180的倍数,15×180<2750<16×180,在少一个内角的情况下,其度数为2750,则可得到此多边形为十八边形,则未知内角度数为130°.故选D.
二.填空题(共8小题)
11 80° .
【解答】解:∵∠1、∠2是△ABC的外角,∠1+∠2=260°,
∴∠A+∠ACB+∠A+∠ABC=260°,∵∠A+∠ACB+∠ABC=180°,∴∠A=80°,故答案为:80°.
12. 180° .
【解答】解:∵AB∥CD,∴∠B+∠C=180°,∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故答案为:180°.
13. 7cm .
【解答】解:①4cm为底,7cm为腰时,周长为:4+7+7=18(cm);
②7cm为底,4cm为腰,周长为:7+4+4=15(cm).∵等腰三角形的周长大于16cm,
∴第三边是7cm.故答案为:7cm.
14. 132° .
【解答】解:∵∠B=66°,∠C=54°,∴∠BAC=180°﹣66°﹣54°=60°,
∵AD是∠BAC的平分线,∴∠BAD=∠BAC=30°,∴∠ADC=∠B+∠BAD=66°+30°=96°,
∵DE平分∠ADC交AC于E,∴∠CDE=∠ADC=48°,∴∠BDE=180°﹣48°=132°.
15.∠B= 57 ,∠C= 33 .
【解答】解:∵∠A=90°,∴∠B+∠C=90°.∵∠B﹣∠C=24°∴∠B=57°,∠C=33°.
16. 8 cm2.
【解答】解:∵AB=AC,AD⊥DC,∴BD=CD,∴S△BEF=S△CEF,∴S阴影部分=S△ABD=S△ABC=×16=8(cm2).
17. 2nπ
【解答】解:第n个多边形中,所有扇形面积之和是:=2nπ.
18.66 度.
【解答】解:因为G是△AFE两外角平分线的交点,所以∠FGE=180°﹣×[360°﹣(180°﹣∠A)]=90°﹣∠A;因为P是△ABC两外角平分线的交点,所以∠P=180°﹣×[360°﹣(180°﹣∠A)]=90°﹣∠A;所以∠P=∠FGE=66°.21*cnjy*com
三.解答题(共7小题)
19.【解答】解:设∠1=∠2=x,则∠3=∠4=2x.因为∠BAC=63°,
所以∠2+∠4=117°,即x+2x=117°,所以x=39°;所以∠3=∠4=78°,
∠DAC=180°﹣∠3﹣∠4=24°.
20.【解答】解:∵CD为△ABC的AB边上的中线,∴AD=BD,
∵△BCD的周长比△ACD的周长大3cm,∴(BC+BD+CD)﹣(AC+AD+CD)=3,
∴BC﹣AC=3,∵BC=8,∴AC=5.
21.【解答】(1)∵∠A+∠B=∠GKH+∠GHK,∠C+∠D=∠GHK+∠HGK,∠E+∠F=∠HGK+∠GHK,
∠A+∠B+∠C+∠D+∠E+∠F=2(∠GKH+∠GHK+∠HGK)=2×180°=360°,故答案为:360°;
(2)如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°﹣∠1﹣∠2+360°﹣∠3﹣∠4+360°﹣∠4﹣∠6+180°﹣∠7﹣∠8+180°﹣∠9﹣∠10=1260°﹣2×360°=540°,故答案为:540°;
(3)①图中共有6个“8字型”;故答案为:6.
②:∵CF平分∠BCD,EF平分∠BED∴∠DEG=∠AEG,∠ACH=∠BCH,
∵在△DGE和△FGC中,∠DGE=∠FGC∴∠D+∠DEG=∠F+∠ACH
∵在△BHC和△FHE中,∠BHC=∠FHE∴∠B+∠BCH=∠F+∠AEG
∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG∴∠D+∠B=2∠F;
∵∠B:∠D:∠F=4:6:x,∠D+∠B=2∠F,∴x=5.
22.【解答】解:(1)(i)在△ABC中,∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,
在△DBC中,∵∠BDC=90°,∴∠DBC+∠DCB=180°﹣90°=90°,
∴∠ABD+∠ACD=140°﹣90°=50°;故答案为:140;90;50.
(ii)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°﹣∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°﹣∠A. 在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB﹣(∠DBC+∠DCB)=180°﹣∠A﹣90°.∴∠ABD+∠ACD=90°﹣∠A.
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ACD﹣∠ABD=90°﹣∠A.
证明如下:在△ABC中,∠ABC+∠ACB=180°﹣∠A. 在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB﹣(∠DBC+∠DCB)=180°﹣∠A﹣90°.∴∠ACD﹣∠ABD=90°﹣∠A.
23.【解答】解:∠BDC=∠A+∠B+∠C.理由如下:作射线AD,如图,
∵∠3=∠B+∠1,∠4=∠2+∠C,∴∠3+∠4=∠1+∠2+∠B+∠C,即∠BDC=∠A+∠B+∠C;
①∵∠BXC=∠A+∠ABX+∠ACX,∴∠ABX+∠ACX=90°﹣58°=32°;
②∵∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠BDC,∠ACE=∠BEC,∴∠DBE﹣∠DCE=∠DCE﹣∠A,
∴∠DCE=(∠DBE+∠A)=×(150°+60°)=105°;
③∵∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,
而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,
∴∠ABG1=∠ABD,∠ACG1=∠ACD,∴10∠BG1C=10∠A+∠ABD+∠ACD,
∴10∠BG1C﹣∠BDC=9∠A,∴∠A=(10×77°﹣140°)=70°.
故答案为32,105,70.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
八上数学第十一章培优提高 多边形培优测试
一.选择题(共11小题)
1.如图,已知在△ABC中,AD是∠BAC的角平分线,AE是BC边上的高,且∠B=25°,∠C=55°,则∠DAE的度数是( )21世纪教育网版权所有
A.15° B.35° C.65° D.75°
2.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A.27 B.35 C.44 D.54
3.如图,BD,CE分别是△ABC的两条高、它们相交于点H,那么下列式子中正确的有( )个.(1)∠DHC=∠A;(2)∠EBH+∠A=90°;(3)∠ACE=∠ABD;(4)∠ECB=∠ABC.
A.1 B.2 C.3 D.4
4.如图所示,∠A+∠B+∠C+∠D+∠E+∠F等于( )
A.180° B.270° C.360° D.540°
第1题图 第3题图 第4题图
5.在美化泸州的建设中,常用正多边形的瓷砖铺地面,在①正三角形、②正方形、③正五边形、④正六边形、⑤正七边形中,如果限于用一种正多边形进行平面镶嵌,能单独镶嵌成一个平面的正多边形有( )21教育网
A.①②③ B.②③④ C.③④⑤ D.①②④
6.多边形的边数增加1时、它的内角和与外角和( )
A.都不变 B.内角和增加180°外角和不变
C.都增加180° D.内角和增加180°外角和减少180°
7.下列命题中,①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360°;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤一个三角形中至少有两个锐角;⑥在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形,其中假命题是( )21cnjy.com
A.①②③④ B.②④⑥ C.②③⑤ D.①②③④⑥
8.一个三角形的两边分别是4和9,而第三边的长为奇数,则第三边的长是( )
A.3或5或7 B.9或11或13 C.5或7或9 D.7或9或11
9.用正三角形和正六边形镶嵌,若每一个顶点周围有m个正三角形、n个正六边形,则m,n满足的关系式是( )【来源:21·世纪·教育·网】
A.2m+3n=12 B.m+n=8 C.2m+n=6 D.m+2n=6
10.在一个n边形中,除了一个内角外,其余(n﹣1)个内角和为2750°,则这个内角是( )
A.140° B.105° C.120° D.130°
第11题图 第12题图 第14题
二.填空题(共8小题)
11.如图,∠1、∠2是△ABC的外角,已知∠1+∠2=260°,求∠A的度数是 .
12.如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3= .21·世纪*教育网
13.一个等腰三角形的两边长分别是4cm和7cm,且它的周长大于16cm,则第三边是 .
14.如图,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠BDE= .【出处:21教育名师】
第16题 第17题
15.在△ABC中,∠A=90°,∠B﹣∠C=24°,那么∠B= 度,∠C= 度.
16.如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F在AD上,若△ABC的面积为16cm2,则图中阴影部分的面积为 cm2.21教育名师原创作品
17.如图中每个阴影部分是以多边形各顶点为圆心,2为半径的扇形,并且所有多边形的每条边长都大于2,则第n个多边形中,所有扇形面积之和是 (结果保留π).
18.如图,G是△AFE两外角平分线的交点,P是△ABC的两外角平分线的交点,F,C在AN上,又B,E在AM上;如果∠FGE=66°,那么∠P= 度.21*cnjy*com
第20题图
一.解答题(共5小题)
19.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
20.如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.www.21-cn-jy.com
21.如图:线段AB、CD相交于点O,连接AD、CB,我们把这个图形称为“8字型”.根据三角形内角和容易得到:∠A+∠D=∠C+∠B.【来源:21cnj*y.co*m】
(1)用“8字型”如图(1):∠A+∠B+∠C+∠D+∠E+∠F= .
(2)造“8字型”如图(2):∠A+∠B+∠C+∠D+∠E+∠F+∠G= .
(3)发现“8字型”如图(3):BE、CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.①图中共有 个“8字型”;【版权所有:21教育】
②若∠B:∠D:∠F=4:6:x,求x的值.
22.如图,将一块直角三角尺DEF放置在锐角三角形ABC上,使得该三角尺的两条直角边DE,DF恰好分别经过点B,C.
(1)如图①,点D在△ABC内.
(i)若∠A=40°,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;2·1·c·n·j·y
(ii)请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
23.如图1的图形,像我们常见的风筝.我们不妨把这样图形叫做“筝形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?
下面就请你发挥你的聪明才智,解决以下问题:
观察“筝形”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=58°,则∠ABX+∠ACX= °;www-2-1-cnjy-com
②如图3,已知DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=150°,则∠DCE= °;
②如图4,已知∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠B G1C=77°,则∠A= °.
参考答案
一.选择题(共11小题)
1A.【解答】解:∵△ABC中,∠B=25°,∠C=55°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣25°﹣55°=100°,∵AD是∠BAC的平分线,∴∠DAC=∠BAC=50°,∵AE是BC边上的高,在直角△AEC中,∵∠EAC=90°﹣∠C=90°﹣55°=35°,∴∠DAE=∠DAC﹣∠EAC=50°﹣35°=15°.故选:A.2-1-c-n-j-y
2C.【解答】解:设这个内角度数为x°,边数为n,∴(n﹣2)×180﹣x=1510,
180n=1870+x=1800+(70+x),∵n为正整数,∴n=11,∴=44,
3C.【解答】解:△ABC的高BD、CE相交于点H,(1)在四边形AEHD中,∠AED+∠ADH=∠A+∠DHE=∠DHE+DHC=180°,所以∠DHC=∠A,(1)正确;
(2)因为∠EHB=∠DHC=∠A,所以∠EBH+∠A=∠EBH+∠A=90°,故(2)正确;
(3)∠ABD+∠A=90°,∠ACE+∠A=90°,∴∠ABD=∠ACE,故(3)正确;
(4)∠ECB+∠ABC=90°,但∠ECB=∠ABC不正确,故(4)错误;
4C.【解答】解:∵∠A+∠F=180°﹣∠AOF,∠B+∠C=180°﹣∠BNC,
∠E+∠D=180°﹣∠DME,又∵∠AOF=∠NOM(对顶角相等),
∠BNC=∠ONM(对顶角相等),∠DME=∠NMO(对顶角相等),
又∵∠NOM+∠ONM+∠NMO=180°(三角形内角和等于180°),
∴∠A+∠B+∠C+∠D+∠E+∠F=180°﹣∠AOF+180°﹣∠BNC+180°﹣∠DME,
=540°﹣(∠NOM+∠ONM+∠NMO),=540°﹣180°,=360°.故选C.
5D.【解答】解:①正三角形每个内角是60°,能被360°整除,所以能单独镶嵌成一个平面;
②正方形每个内角是90°,能被360°整除,所以能单独镶嵌成一个平面;
③正五边形每个内角是108°,不能被360°整除,所以不能单独镶嵌成一个平面;
④正六边形每个内角是120°,能被360°整除,所以能单独镶嵌成一个平面;
⑤正七边形每个内角的度数不能被360°整除,所以不能单独镶嵌成一个平面.
故能单独镶嵌成一个平面的正多边形有:①②④.故选D.
6B.【解答】解:根据n边形的内角和可以表示成(n﹣2) 180°,
可以得到增加一条边时,边数变为n+1,
则内角和是(n﹣1) 180°,因而内角和增加:(n﹣1) 180°﹣(n﹣2) 180°=180°.
多边形外角和为360°,故选B.
7D.【解答】解:①错误.直角三角形的三条高(或高的延长线)的交点在直角顶点处.
②错误.应该是一个多边形的边数每增加一条,这个多边形的内角和就增加180°.
③错误.应该是两条平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
④错误.应该是三角形的一个外角等于不相邻的两个内角的和.
⑤正确.一个三角形中至少有两个锐角.
⑥错误.设∠A=6x,则∠B=3x,∠C=2x,由题意6x+3x+2x=180,解得x=()°,∴∠A、∠B、∠C中没有直角,∴△ABC表示直角三角形.故选D.
8D.【解答】解:根据题意得:5<第三边<13,又∵第三边的长为奇数,
∴第三边的长是7,9,11.故选D.
9D.【解答】解:正多边形的平面镶嵌,每一个顶点处的几个角之和应为360度,
而正三角形和正六边形内角分别为60°、120°,根据题意可知60°×m+120°×n=360°,化简得到m+2n=6.故选D.21·cn·jy·com
10D.【解答】解:多边形内角和(n﹣2)×180°,则多边形内角和一定是180的倍数,15×180<2750<16×180,在少一个内角的情况下,其度数为2750,则可得到此多边形为十八边形,则未知内角度数为130°.故选D.
二.填空题(共8小题)
11 80° .
【解答】解:∵∠1、∠2是△ABC的外角,∠1+∠2=260°,
∴∠A+∠ACB+∠A+∠ABC=260°,∵∠A+∠ACB+∠ABC=180°,∴∠A=80°,故答案为:80°.
12. 180° .
【解答】解:∵AB∥CD,∴∠B+∠C=180°,∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故答案为:180°.
13. 7cm .
【解答】解:①4cm为底,7cm为腰时,周长为:4+7+7=18(cm);
②7cm为底,4cm为腰,周长为:7+4+4=15(cm).∵等腰三角形的周长大于16cm,
∴第三边是7cm.故答案为:7cm.
14. 132° .
【解答】解:∵∠B=66°,∠C=54°,∴∠BAC=180°﹣66°﹣54°=60°,
∵AD是∠BAC的平分线,∴∠BAD=∠BAC=30°,∴∠ADC=∠B+∠BAD=66°+30°=96°,
∵DE平分∠ADC交AC于E,∴∠CDE=∠ADC=48°,∴∠BDE=180°﹣48°=132°.
15.∠B= 57 ,∠C= 33 .
【解答】解:∵∠A=90°,∴∠B+∠C=90°.∵∠B﹣∠C=24°∴∠B=57°,∠C=33°.
16. 8 cm2.
【解答】解:∵AB=AC,AD⊥DC,∴BD=CD,∴S△BEF=S△CEF,∴S阴影部分=S△ABD=S△ABC=×16=8(cm2).
17. 2nπ
【解答】解:第n个多边形中,所有扇形面积之和是:=2nπ.
18.66 度.
【解答】解:因为G是△AFE两外角平分线的交点,所以∠FGE=180°﹣×[360°﹣(180°﹣∠A)]=90°﹣∠A;因为P是△ABC两外角平分线的交点,所以∠P=180°﹣×[360°﹣(180°﹣∠A)]=90°﹣∠A;所以∠P=∠FGE=66°.21*cnjy*com
三.解答题(共7小题)
19.【解答】解:设∠1=∠2=x,则∠3=∠4=2x.因为∠BAC=63°,
所以∠2+∠4=117°,即x+2x=117°,所以x=39°;所以∠3=∠4=78°,
∠DAC=180°﹣∠3﹣∠4=24°.
20.【解答】解:∵CD为△ABC的AB边上的中线,∴AD=BD,
∵△BCD的周长比△ACD的周长大3cm,∴(BC+BD+CD)﹣(AC+AD+CD)=3,
∴BC﹣AC=3,∵BC=8,∴AC=5.
21.【解答】(1)∵∠A+∠B=∠GKH+∠GHK,∠C+∠D=∠GHK+∠HGK,∠E+∠F=∠HGK+∠GHK,
∠A+∠B+∠C+∠D+∠E+∠F=2(∠GKH+∠GHK+∠HGK)=2×180°=360°,故答案为:360°;
(2)如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°﹣∠1﹣∠2+360°﹣∠3﹣∠4+360°﹣∠4﹣∠6+180°﹣∠7﹣∠8+180°﹣∠9﹣∠10=1260°﹣2×360°=540°,故答案为:540°;
(3)①图中共有6个“8字型”;故答案为:6.
②:∵CF平分∠BCD,EF平分∠BED∴∠DEG=∠AEG,∠ACH=∠BCH,
∵在△DGE和△FGC中,∠DGE=∠FGC∴∠D+∠DEG=∠F+∠ACH
∵在△BHC和△FHE中,∠BHC=∠FHE∴∠B+∠BCH=∠F+∠AEG
∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG∴∠D+∠B=2∠F;
∵∠B:∠D:∠F=4:6:x,∠D+∠B=2∠F,∴x=5.
22.【解答】解:(1)(i)在△ABC中,∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,
在△DBC中,∵∠BDC=90°,∴∠DBC+∠DCB=180°﹣90°=90°,
∴∠ABD+∠ACD=140°﹣90°=50°;故答案为:140;90;50.
(ii)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°﹣∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°﹣∠A. 在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB﹣(∠DBC+∠DCB)=180°﹣∠A﹣90°.∴∠ABD+∠ACD=90°﹣∠A.
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ACD﹣∠ABD=90°﹣∠A.
证明如下:在△ABC中,∠ABC+∠ACB=180°﹣∠A. 在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB﹣(∠DBC+∠DCB)=180°﹣∠A﹣90°.∴∠ACD﹣∠ABD=90°﹣∠A.
23.【解答】解:∠BDC=∠A+∠B+∠C.理由如下:作射线AD,如图,
∵∠3=∠B+∠1,∠4=∠2+∠C,∴∠3+∠4=∠1+∠2+∠B+∠C,即∠BDC=∠A+∠B+∠C;
①∵∠BXC=∠A+∠ABX+∠ACX,∴∠ABX+∠ACX=90°﹣58°=32°;
②∵∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠BDC,∠ACE=∠BEC,∴∠DBE﹣∠DCE=∠DCE﹣∠A,
∴∠DCE=(∠DBE+∠A)=×(150°+60°)=105°;
③∵∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,
而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,
∴∠ABG1=∠ABD,∠ACG1=∠ACD,∴10∠BG1C=10∠A+∠ABD+∠ACD,
∴10∠BG1C﹣∠BDC=9∠A,∴∠A=(10×77°﹣140°)=70°.
故答案为32,105,70.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
