13.3.1等腰三角形培优提高试题
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
八上数学第十三章培优提高 等腰三角形
一.选择题(共10小题)
1.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
A. 2 B.3 C.4 D.5
2.在△ABC中,AB=AC,∠B=50°,∠A的度数为( )
A.50° B.65° C.75° D.80°
3.等腰三角形的周长为26cm,一边长为6cm,那么腰长为( )
A.6cm B.10cm C.6cm或10cm D.14cm
4.等腰三角形是轴对称图形,它的对称轴是( )
A.底边上的高 B.腰上的高所在的直线 C.顶角的平分线所在的直线 D.过顶点的直线
5.如图,OB,OC分别平分∠ABC与∠ACB,MN∥BC,若AB=24,AC=36,则△AMN的周长是( )
A.60 B.66 C.72 D.7821cnjy.com
6.如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
A.74° B.32° C.22° D.16°
7.如图,∠MON=43°,点A在射线OM上,动点P在射线ON上滑动,要使△AOP为等腰三角形,那么满足条件的点P共有( )www.21-cn-jy.com
A.1个 B.2个 C.3个 D.4个
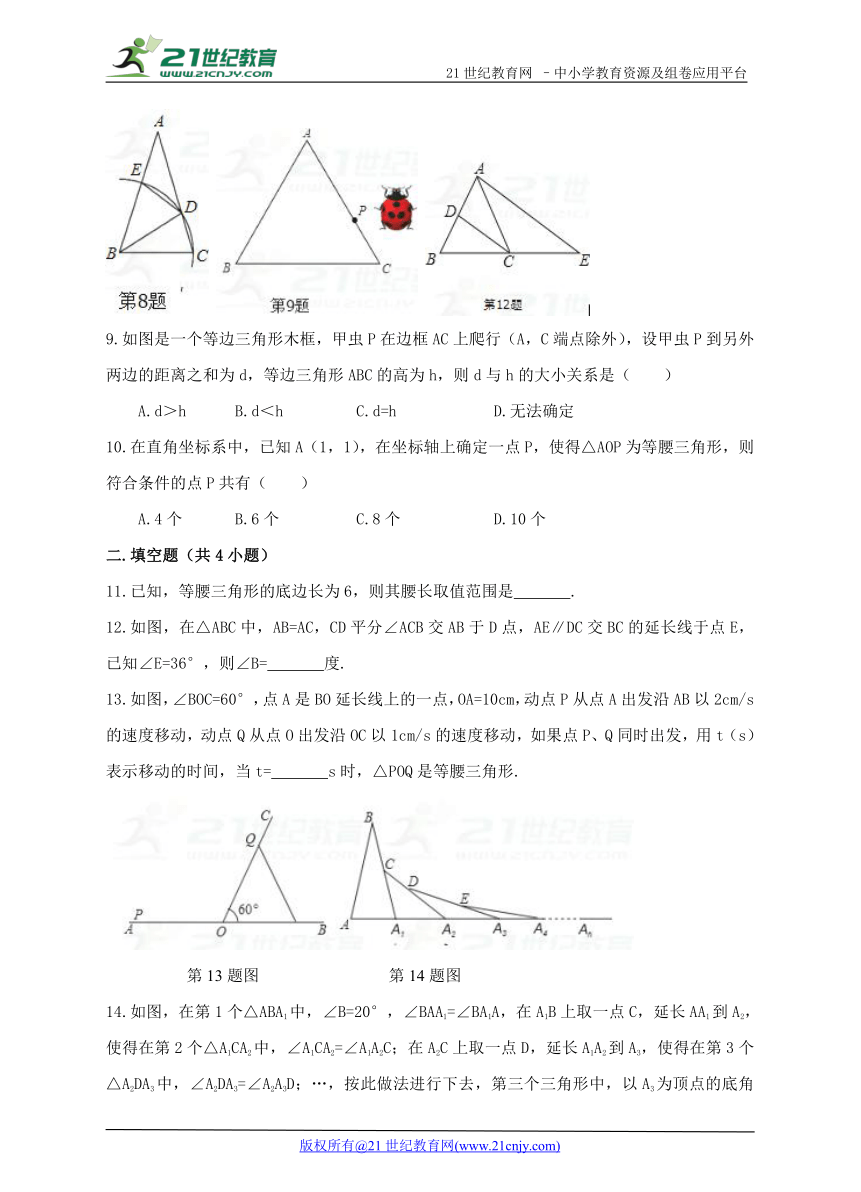
8.如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )2·1·c·n·j·y
A.67.5° B.52.5° C.45° D.75°.
9.如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( )
A.d>h B.d<h C.d=h D.无法确定
10.在直角坐标系中,已知A(1,1),在坐标轴上确定一点P,使得△AOP为等腰三角形,则符合条件的点P共有( )2-1-c-n-j-y
A.4个 B.6个 C.8个 D.10个
二.填空题(共4小题)
11.已知,等腰三角形的底边长为6,则其腰长取值范围是 .
12.如图,在△ABC中,AB=AC,CD平分∠ACB交AB于D点,AE∥DC交BC的延长线于点E,已知∠E=36°,则∠B= 度.21*cnjy*com
13.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t= s时,△POQ是等腰三角形.【来源:21cnj*y.co*m】
第13题图 第14题图
14.如图,在第1个△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第三个三角形中,以A3为顶点的底角的度数为 ;第n个三角形中以An为顶点的底角的度数为 .
三.解答题(共6小题)
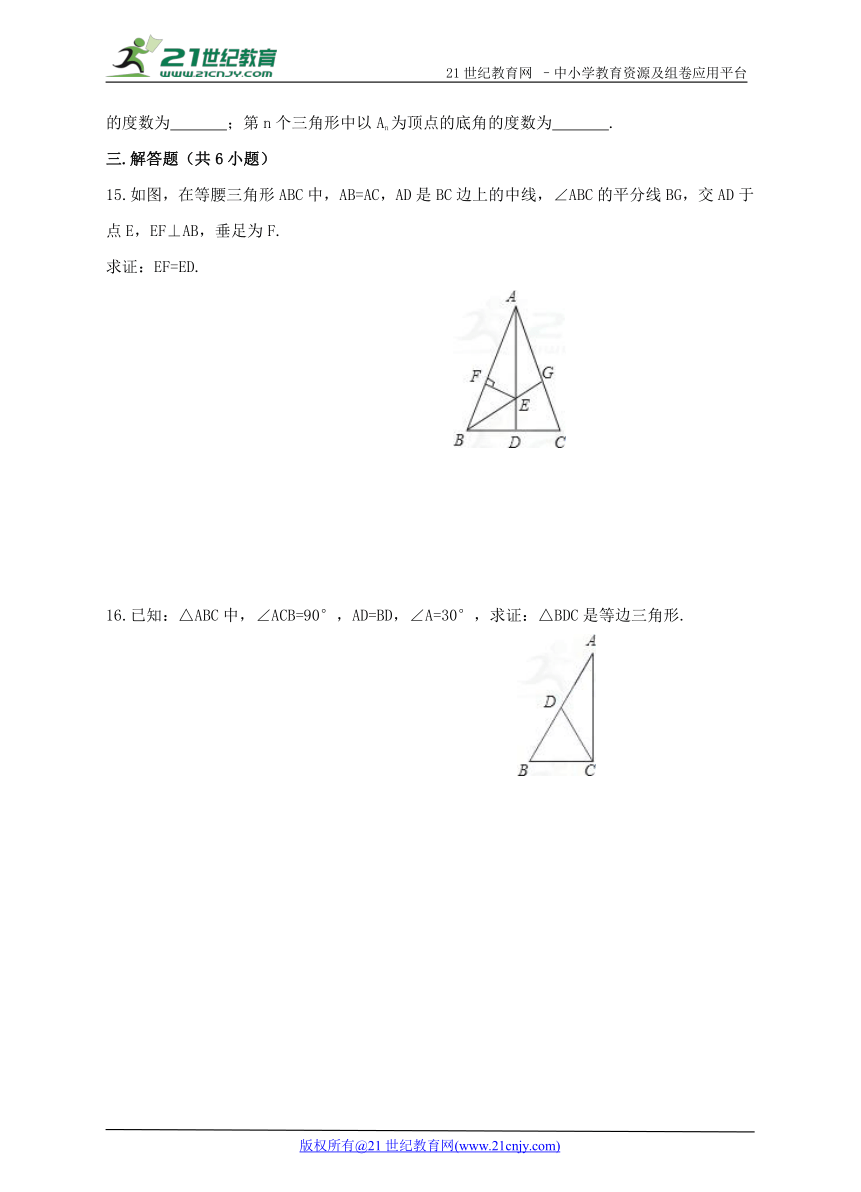
15.如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG,交AD于点E,EF⊥AB,垂足为F.【来源:21·世纪·教育·网】
求证:EF=ED.
16.已知:△ABC中,∠ACB=90°,AD=BD,∠A=30°,求证:△BDC是等边三角形.
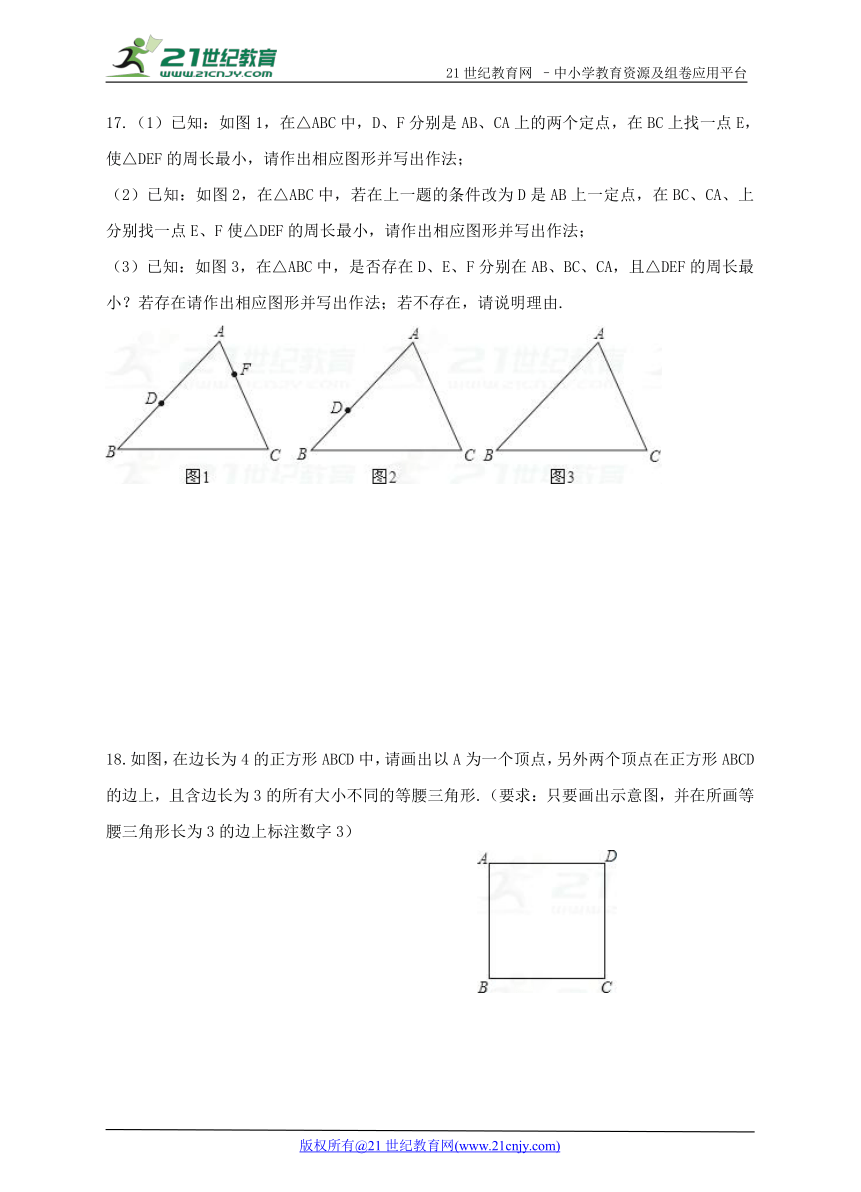
17.(1)已知:如图1,在△ABC中,D、F分别是AB、CA上的两个定点,在BC上找一点E,使△DEF的周长最小,请作出相应图形并写出作法;【出处:21教育名师】
(2)已知:如图2,在△ABC中,若在上一题的条件改为D是AB上一定点,在BC、CA、上分别找一点E、F使△DEF的周长最小,请作出相应图形并写出作法;
(3)已知:如图3,在△ABC中,是否存在D、E、F分别在AB、BC、CA,且△DEF的周长最小?若存在请作出相应图形并写出作法;若不存在,请说明理由.【版权所有:21教育】
18.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)21教育名师原创作品
19.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.21*cnjy*com
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
20.如图,在△ABC中,AB=AC,∠B=30°,点D从点B出发,沿B→C方向运动到C(D不与B、C重合),连接AD,作∠ADE=30°,DE交线段AC于E.
(1)在点D的运动过程中,若∠BDA=100°,求∠DEC的大小;
(2)在点D的运动过程中,若AB=DC,请证明△ABD≌△DCE;
(3)若BC=6cm,点D的运动速度是1cm/s,运动时间为t(s).在点D的运动过程中,是否存在这样的t,使得△ADE的形状是直角三角形?若存在,请求出符合条件的t的值;若不存在,请说明理由.
参考答案
1D.【解答】解:∵∠B=∠C,∴AB=AC=5.故选D.
2D.【解答】解:∵在△ABC中,AB=AC,∠B=50°∴∠A=180﹣50×2=80°故选D.
3B.【解答】解:①当6cm为腰长时,则腰长为6cm,底边=26﹣6﹣6=14cm,因为14>6+6,所以不能构成三角形;②当6cm为底边时,则腰长=(26﹣6)÷2=10cm,因为6﹣6<10<6+6,所以能构成三角形;故选B.21·cn·jy·com
4.C.【解答】解:等腰三角形是轴对称图形,它的对称轴是:顶角的平分线所在的直线.故选:C.
5.A.【解答】解:∵OB平分∠ABC,∴∠MBO=∠CBO,∵MN∥BC,
∴∠MOB=∠CBO,∴∠MOB=∠MBO,∴MB=MO,同理NC=NO;
∵△AMN的周长=AM+MO+ON+AN=AB+AC=24+36=60.故选A.
6.B.【解答】解:∵CD=CE,∠D=74°,∴∠DEC=∠D=74°,
∴∠C=180°﹣74°﹣74°=32°,∵AB∥CD,∴∠B=∠C=32°,故选B.
7.C.【解答】解:当∠O=∠OAP时,构成等腰三角形可找到一个P点.
当∠O=∠OPA时,构成等腰三角形可找到一个P点.
当∠OAP=∠OPA时,构成等腰三角形可找到一个P点.故可找到三个P点.
8.A.【解答】解:∵AB=AC,∴∠ABC=∠ACB,∵∠A=30°,
∴∠ABC=∠ACB=(180°﹣30°)=75°,∵以B为圆心,BC长为半径画弧,
∴BE=BD=BC,∴∠BDC=∠ACB=75°,∴∠CBD=180°﹣75°﹣75°=30°,
∴∠DBE=75°﹣30°=45°,∴∠BED=∠BDE=(180°﹣45°)=67.5°.
9.C【解答】解:如图,连接BP,过点P做PD⊥BC,PE⊥AB,分别交BC,AB于点D,E,∴S△ABC=S△BPC+S△BPA=BC PD+AB PE=BC PD+BC PE=BC(PD+PE)=d BC=h BC ∴d=h. 故选:C.21教育网
10.C.【解答】解:如图所示,AO为底边时,点P可以有两个位置,
AO为腰长时,点P可以有6个位置,所以,符合条件的点P共有8个.故选C.
二.填空题(共4小题)
11.x>3
【解答】解:设等腰三角形的腰长为x,∵等腰三角形的底边长6,等腰三角形的两腰相等,且三角形中任意两边之和大于第三边,∴2x>6,∴x>3.www-2-1-cnjy-com
12. 72 度.
【解答】解:∵∠E=36°,AE∥DC,∴∠E=∠BCD=36°,
∵CD平分∠ACB,∴∠ACB=72°;∵AB=AC,∴∠B=∠ACB=72°.
13. 或10
【解答】解:当PO=QO时,△POQ是等腰三角形;
如图1所示:∵PO=AO﹣AP=10﹣2t,OQ=1t∴当PO=QO时,
10﹣2t=t 解得t=;
当PO=QO时,△POQ是等腰三角形;
如图2所示:
∵PO=AP﹣AO=2t﹣10,OQ=1t;∴当PO=QO时,2t﹣10=t;解得t=10;
故答案为:或10.
14 20° ; .
【解答】解:∵在△ABA1中,∠B=20°,AB=A1B,
∴∠BA1A===80°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1=∠BA1A=×80°=40°;
同理可得,
∠DA3A2=20°,∠EA4A3=10°,
∴第n个三角形的以An为顶点的底角的度数=.
故答案为;20°,.
三.解答题(共7小题)
15.【解答】证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC.
∵BG平分∠ABC,EF⊥AB,
∴EF=ED.
16.【解答】证明:∵△ABC中,∠ACB=90°,∠A=30°(已知),
∴∠A+∠B=90°(直角三角形两锐角互余),
∴∠B=90°﹣∠A=90°﹣30°=60°,
∵△ABC中,∠ACB=90°,∠A=30°(已知),
∴BC=AB=BD(在直角三角形中,一个锐角等于30,那么它所对的直角边等于斜边的一半),
∴△BDC是等边三角形(有一个角是60°角的等腰三角形是等边三角形).
17.【解答】解:(1)如图1,作点D关于BC的对称点D′连接D′F交BC于E,则△DEF为所求;
(2)如图2,作点D关于BC、AC的对称点D′、D″,连接D′D″交BC、AC于E、F,则△DEF为所求;21世纪教育网版权所有
(3)如图3,过A作AE⊥BC,过点E分别作AB、AC的对称点E′、E″连接E′E″交AB、AC于D、E,则△DEF为所求. 21·世纪*教育网
18.【解答】解:满足条件的所有图形如图所示:
19.【解答】解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,
∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,小;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,∴∠DEC+∠EDC=140°,又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,又∵AB=DC=2,
∴△ABD≌△DCE(AAS),
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
理由:∵∠BDA=110°时,∴∠ADC=70°,
∵∠C=40°,∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,
∴∠DAC=∠AED,∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,∴∠ADC=100°,∵∠C=40°,
∴∠DAC=40°,∴∠DAC=∠ADE,∴△ADE的形状是等腰三角形.
20.【解答】解:(1)∵AB=AC,∠B=30°,∴∠C=∠B=30°,
∵∠BDA=100°,∠ADE=30°,∴∠EDC=180°﹣100°﹣30°=50°,
∴∠DEC=180°﹣50°﹣30°=100°;
(2)∵∠C=30°,∴∠CED+∠CDE=150°,∵∠ADE=30°,
∴∠ADB+∠CDE=150°,∴∠CED=∠ADB,
在△ABD和△DCE中,,∴△ABD≌△DCE(AAS);
(3)存在,∵AB=AC,∠B=30°,∴∠BAC=120°,
∵BC=6cm,点D的运动速度是1cm/s,运动时间为t(s),∴BD=t,CD=6﹣t,
①如图1,当∠DAE=90,则∠BAD=30°,∴∠BAD=∠B=30°,
∴AD=BD=t,∵∠C=30°,∴CD=2AD,即6﹣t=2t,∴t=2;
②如图2,当∠AED=90°时,则∠DAE=60°,
∴AD平分∠BAC,∴BD=CD,即t=6﹣t,∴t=3,
综上所述,当t=2或3时,△ADE的形状是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
八上数学第十三章培优提高 等腰三角形
一.选择题(共10小题)
1.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
A. 2 B.3 C.4 D.5
2.在△ABC中,AB=AC,∠B=50°,∠A的度数为( )
A.50° B.65° C.75° D.80°
3.等腰三角形的周长为26cm,一边长为6cm,那么腰长为( )
A.6cm B.10cm C.6cm或10cm D.14cm
4.等腰三角形是轴对称图形,它的对称轴是( )
A.底边上的高 B.腰上的高所在的直线 C.顶角的平分线所在的直线 D.过顶点的直线
5.如图,OB,OC分别平分∠ABC与∠ACB,MN∥BC,若AB=24,AC=36,则△AMN的周长是( )
A.60 B.66 C.72 D.7821cnjy.com
6.如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
A.74° B.32° C.22° D.16°
7.如图,∠MON=43°,点A在射线OM上,动点P在射线ON上滑动,要使△AOP为等腰三角形,那么满足条件的点P共有( )www.21-cn-jy.com
A.1个 B.2个 C.3个 D.4个
8.如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )2·1·c·n·j·y
A.67.5° B.52.5° C.45° D.75°.
9.如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( )
A.d>h B.d<h C.d=h D.无法确定
10.在直角坐标系中,已知A(1,1),在坐标轴上确定一点P,使得△AOP为等腰三角形,则符合条件的点P共有( )2-1-c-n-j-y
A.4个 B.6个 C.8个 D.10个
二.填空题(共4小题)
11.已知,等腰三角形的底边长为6,则其腰长取值范围是 .
12.如图,在△ABC中,AB=AC,CD平分∠ACB交AB于D点,AE∥DC交BC的延长线于点E,已知∠E=36°,则∠B= 度.21*cnjy*com
13.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t= s时,△POQ是等腰三角形.【来源:21cnj*y.co*m】
第13题图 第14题图
14.如图,在第1个△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第三个三角形中,以A3为顶点的底角的度数为 ;第n个三角形中以An为顶点的底角的度数为 .
三.解答题(共6小题)
15.如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG,交AD于点E,EF⊥AB,垂足为F.【来源:21·世纪·教育·网】
求证:EF=ED.
16.已知:△ABC中,∠ACB=90°,AD=BD,∠A=30°,求证:△BDC是等边三角形.
17.(1)已知:如图1,在△ABC中,D、F分别是AB、CA上的两个定点,在BC上找一点E,使△DEF的周长最小,请作出相应图形并写出作法;【出处:21教育名师】
(2)已知:如图2,在△ABC中,若在上一题的条件改为D是AB上一定点,在BC、CA、上分别找一点E、F使△DEF的周长最小,请作出相应图形并写出作法;
(3)已知:如图3,在△ABC中,是否存在D、E、F分别在AB、BC、CA,且△DEF的周长最小?若存在请作出相应图形并写出作法;若不存在,请说明理由.【版权所有:21教育】
18.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)21教育名师原创作品
19.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.21*cnjy*com
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
20.如图,在△ABC中,AB=AC,∠B=30°,点D从点B出发,沿B→C方向运动到C(D不与B、C重合),连接AD,作∠ADE=30°,DE交线段AC于E.
(1)在点D的运动过程中,若∠BDA=100°,求∠DEC的大小;
(2)在点D的运动过程中,若AB=DC,请证明△ABD≌△DCE;
(3)若BC=6cm,点D的运动速度是1cm/s,运动时间为t(s).在点D的运动过程中,是否存在这样的t,使得△ADE的形状是直角三角形?若存在,请求出符合条件的t的值;若不存在,请说明理由.
参考答案
1D.【解答】解:∵∠B=∠C,∴AB=AC=5.故选D.
2D.【解答】解:∵在△ABC中,AB=AC,∠B=50°∴∠A=180﹣50×2=80°故选D.
3B.【解答】解:①当6cm为腰长时,则腰长为6cm,底边=26﹣6﹣6=14cm,因为14>6+6,所以不能构成三角形;②当6cm为底边时,则腰长=(26﹣6)÷2=10cm,因为6﹣6<10<6+6,所以能构成三角形;故选B.21·cn·jy·com
4.C.【解答】解:等腰三角形是轴对称图形,它的对称轴是:顶角的平分线所在的直线.故选:C.
5.A.【解答】解:∵OB平分∠ABC,∴∠MBO=∠CBO,∵MN∥BC,
∴∠MOB=∠CBO,∴∠MOB=∠MBO,∴MB=MO,同理NC=NO;
∵△AMN的周长=AM+MO+ON+AN=AB+AC=24+36=60.故选A.
6.B.【解答】解:∵CD=CE,∠D=74°,∴∠DEC=∠D=74°,
∴∠C=180°﹣74°﹣74°=32°,∵AB∥CD,∴∠B=∠C=32°,故选B.
7.C.【解答】解:当∠O=∠OAP时,构成等腰三角形可找到一个P点.
当∠O=∠OPA时,构成等腰三角形可找到一个P点.
当∠OAP=∠OPA时,构成等腰三角形可找到一个P点.故可找到三个P点.
8.A.【解答】解:∵AB=AC,∴∠ABC=∠ACB,∵∠A=30°,
∴∠ABC=∠ACB=(180°﹣30°)=75°,∵以B为圆心,BC长为半径画弧,
∴BE=BD=BC,∴∠BDC=∠ACB=75°,∴∠CBD=180°﹣75°﹣75°=30°,
∴∠DBE=75°﹣30°=45°,∴∠BED=∠BDE=(180°﹣45°)=67.5°.
9.C【解答】解:如图,连接BP,过点P做PD⊥BC,PE⊥AB,分别交BC,AB于点D,E,∴S△ABC=S△BPC+S△BPA=BC PD+AB PE=BC PD+BC PE=BC(PD+PE)=d BC=h BC ∴d=h. 故选:C.21教育网
10.C.【解答】解:如图所示,AO为底边时,点P可以有两个位置,
AO为腰长时,点P可以有6个位置,所以,符合条件的点P共有8个.故选C.
二.填空题(共4小题)
11.x>3
【解答】解:设等腰三角形的腰长为x,∵等腰三角形的底边长6,等腰三角形的两腰相等,且三角形中任意两边之和大于第三边,∴2x>6,∴x>3.www-2-1-cnjy-com
12. 72 度.
【解答】解:∵∠E=36°,AE∥DC,∴∠E=∠BCD=36°,
∵CD平分∠ACB,∴∠ACB=72°;∵AB=AC,∴∠B=∠ACB=72°.
13. 或10
【解答】解:当PO=QO时,△POQ是等腰三角形;
如图1所示:∵PO=AO﹣AP=10﹣2t,OQ=1t∴当PO=QO时,
10﹣2t=t 解得t=;
当PO=QO时,△POQ是等腰三角形;
如图2所示:
∵PO=AP﹣AO=2t﹣10,OQ=1t;∴当PO=QO时,2t﹣10=t;解得t=10;
故答案为:或10.
14 20° ; .
【解答】解:∵在△ABA1中,∠B=20°,AB=A1B,
∴∠BA1A===80°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1=∠BA1A=×80°=40°;
同理可得,
∠DA3A2=20°,∠EA4A3=10°,
∴第n个三角形的以An为顶点的底角的度数=.
故答案为;20°,.
三.解答题(共7小题)
15.【解答】证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC.
∵BG平分∠ABC,EF⊥AB,
∴EF=ED.
16.【解答】证明:∵△ABC中,∠ACB=90°,∠A=30°(已知),
∴∠A+∠B=90°(直角三角形两锐角互余),
∴∠B=90°﹣∠A=90°﹣30°=60°,
∵△ABC中,∠ACB=90°,∠A=30°(已知),
∴BC=AB=BD(在直角三角形中,一个锐角等于30,那么它所对的直角边等于斜边的一半),
∴△BDC是等边三角形(有一个角是60°角的等腰三角形是等边三角形).
17.【解答】解:(1)如图1,作点D关于BC的对称点D′连接D′F交BC于E,则△DEF为所求;
(2)如图2,作点D关于BC、AC的对称点D′、D″,连接D′D″交BC、AC于E、F,则△DEF为所求;21世纪教育网版权所有
(3)如图3,过A作AE⊥BC,过点E分别作AB、AC的对称点E′、E″连接E′E″交AB、AC于D、E,则△DEF为所求. 21·世纪*教育网
18.【解答】解:满足条件的所有图形如图所示:
19.【解答】解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,
∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,小;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,∴∠DEC+∠EDC=140°,又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,又∵AB=DC=2,
∴△ABD≌△DCE(AAS),
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
理由:∵∠BDA=110°时,∴∠ADC=70°,
∵∠C=40°,∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,
∴∠DAC=∠AED,∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,∴∠ADC=100°,∵∠C=40°,
∴∠DAC=40°,∴∠DAC=∠ADE,∴△ADE的形状是等腰三角形.
20.【解答】解:(1)∵AB=AC,∠B=30°,∴∠C=∠B=30°,
∵∠BDA=100°,∠ADE=30°,∴∠EDC=180°﹣100°﹣30°=50°,
∴∠DEC=180°﹣50°﹣30°=100°;
(2)∵∠C=30°,∴∠CED+∠CDE=150°,∵∠ADE=30°,
∴∠ADB+∠CDE=150°,∴∠CED=∠ADB,
在△ABD和△DCE中,,∴△ABD≌△DCE(AAS);
(3)存在,∵AB=AC,∠B=30°,∴∠BAC=120°,
∵BC=6cm,点D的运动速度是1cm/s,运动时间为t(s),∴BD=t,CD=6﹣t,
①如图1,当∠DAE=90,则∠BAD=30°,∴∠BAD=∠B=30°,
∴AD=BD=t,∵∠C=30°,∴CD=2AD,即6﹣t=2t,∴t=2;
②如图2,当∠AED=90°时,则∠DAE=60°,
∴AD平分∠BAC,∴BD=CD,即t=6﹣t,∴t=3,
综上所述,当t=2或3时,△ADE的形状是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
