13.3.2 等边三角形培优提高试题
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
八上数学第十三章培优提高 等边三角形
一.选择题(共9小题)
1.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
2.已知∠AOB=30°,点P在∠AOB的内部,点C与点P关于OB对称,点D与点P关于OA对称,则△OCD是( )21世纪教育网版权所有
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
3.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )www.21-cn-jy.com
A.6cm B.5cm C.4cm D.3cm
4.如图,在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD,AD=2,则BC等于( )
A.4 B.5 C.6 D.8
5.如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )2·1·c·n·j·y
A.△ACE≌△BCD B.△BGC≌△AFC C.△ADB≌△CEA D.△DCG≌△ECF
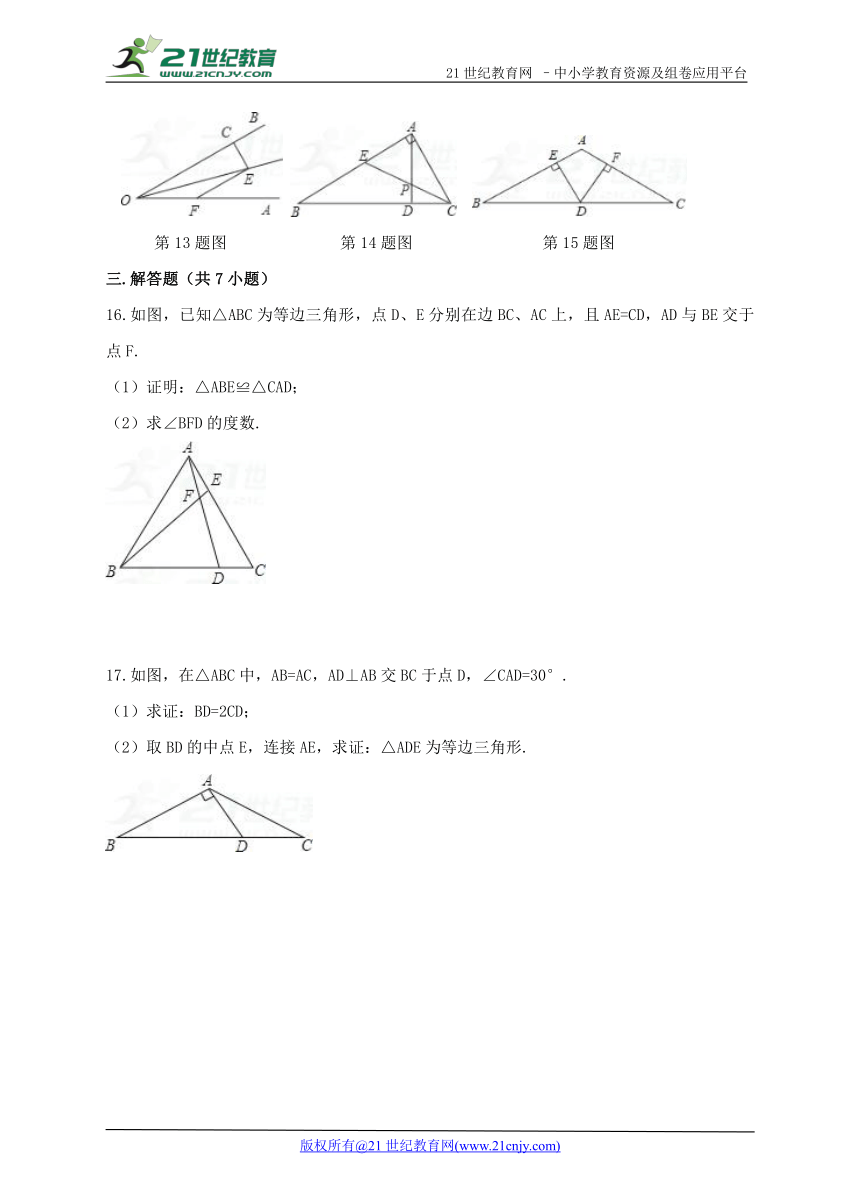
第3题图 第4题图 第5题图
6.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )
A.3cm B.4cm C.4.5cm D.5cm
7.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( )
A.2cm B.4cm C.8cm D.16cm
8.如图,已知△ABC和△CDE都是等边三角形,AD、BE交于点F,则∠AFB等于( )
A.50° B.60° C.45° D.∠BCD
9.如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
A. B. C. D.
第6题图 第8题图 第9题图
二.填空题(共6小题)
10.如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为 .
11.如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠EFD= °.21·世纪*教育网
12.如图,△ABC、△ADE均为等边三角形,AD平分∠BAC交BC于D,DE交AB于F,则下列结论:①AD⊥BC;②EF=FD; ③BE=BD,其中正确的有 (填序号).
第10题图 第11题图 第12题图
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=3,则EF的长为 .
14.如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB的平分线,且交AD于P点.如果AP=2,则AB的长为 .2-1-c-n-j-y
15.如图是屋顶的“人字形“钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为中柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF= m.
第13题图 第14题图 第15题图
三.解答题(共7小题)
16.如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.www-2-1-cnjy-com
(1)证明:△ABE≌△CAD;
(2)求∠BFD的度数.
17.如图,在△ABC中,AB=AC,AD⊥AB交BC于点D,∠CAD=30°.
(1)求证:BD=2CD;
(2)取BD的中点E,连接AE,求证:△ADE为等边三角形.
18.如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.
(1)求作点P,使P到A、B两村的距离相等.(不写作法,保留作图痕迹)
(2)求作点Q,使Q到A、B两村的水管最省料.(不写作法,保留作图痕迹)
19.如图,一艘轮船以15海里/时的速度由南向北航行,在A处测得小岛P在北偏西15°方向上,两小时后,轮船在B处测得小岛P在北偏西30°方向上.在小岛周围18海里内有暗礁,若轮船不改变方向仍继续向前航行,问:有无触礁的危险?并说明你的理由.
20.如图,在△ABC,∠ACB=90°,CD、CE三等分∠ACB,CD⊥AB,
求证:(1)AB=2BC;(2)CE=AE=EB.
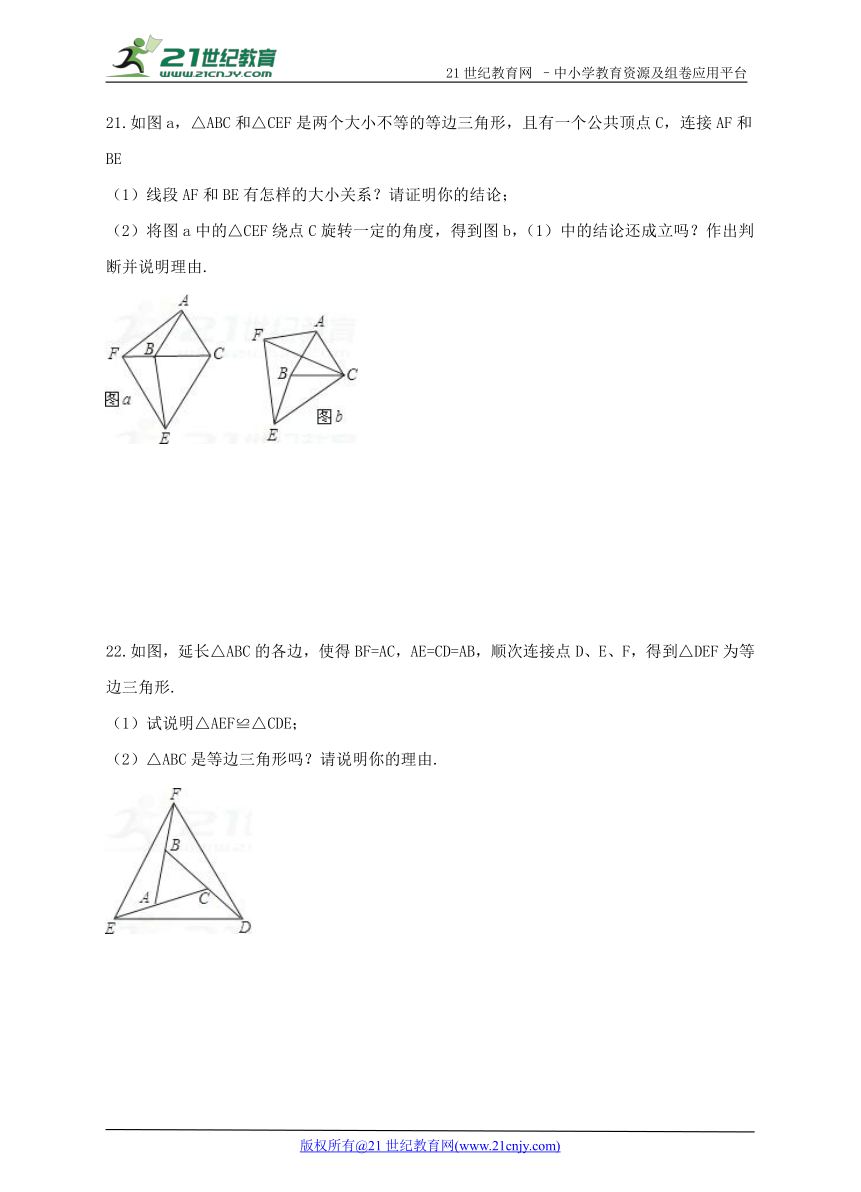
21.如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE
(1)线段AF和BE有怎样的大小关系?请证明你的结论;
(2)将图a中的△CEF绕点C旋转一定的角度,得到图b,(1)中的结论还成立吗?作出判断并说明理由.21教育网
22.如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接点D、E、F,得到△DEF为等边三角形.21cnjy.com
(1)试说明△AEF≌△CDE;
(2)△ABC是等边三角形吗?请说明你的理由.
参考答案与试题解析
一.选择题(共9小题)
1D.【解答】解:①两个角为60度,则第三个角也是60度,则其是等边三角形,故正确;
②这是等边三角形的判定2,故正确;③三个外角相等则三个内角相等,则其是等边三角形,故正确;④根据等边三角形三线合一性质,故正确.所以都正确.故选D.
2B.【解答】解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为D、C,
∴OP=OD=OC且∠DOC=2∠AOB=60°,∴△OCD是等边三角形.故选B.
3D.【解答】解:∵在△ABC中,∠ACB=90°,∠B=15°,∴∠BAC=90°﹣15°=75°,
∵DE垂直平分AB,交BC于点E,BE=6cm,∴BE=AE=6cm,∴∠EAB=∠B=15°,
∴∠EAC=75°﹣15°=60°,∵∠C=90°,∴∠AEC=30°,∴AC=AE=6cm=3cm,
故选D.
4C.【解答】解:∵AB=AC,∠C=30°,∴∠B=∠C=30°,∠BAC=120°,
∵AB⊥AD,∴∠BAD=90°,∵AD=2,∴BD=2AD=4,∵∠DAC=120°﹣90°=30°,
∴∠DAC=∠C,∴AD=DC=2,∴BC=BD+DC=4+2=6,故选C.
5C.【解答】解:∵△ABC和△CDE都是等边三角形,∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACD=∠ECD+∠ACD,即∠BCD=∠ACE,
∴在△BCD和△ACE中 ,∴△BCD≌△ACE(SAS),故A成立,
∴∠DBC=∠CAE,∵∠BCA=∠ECD=60°,∴∠ACD=60°,
在△BGC和△AFC中,∴△BGC≌△AFC,故B成立,
∵△BCD≌△ACE,∴∠CDB=∠CEA,
在△DCG和△ECF中,∴△DCG≌△ECF,故D成立,故选:C.
6A.【解答】解:由折叠可得AD=A′D;AE=A′E,∴阴影部分图形的周长为AB+BC+AC=3cm.
7C.【解答】解:在Rt△ABC中,CD是斜边AB上的高∴∠B+∠A=∠DCA+∠A=90°
∴∠DCA=∠B=30°∴AC=2AD=4,∴AB=2AC=8cm.故选C.
8B.【解答】解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,
在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE,
设AD与BC相交于P点,在△ACP和△BFP中,有一对对顶角,∴∠AFB=∠ACB=60°
9C.【解答】解:连接BE,与AD交于点M.则BE就是EM+CM的最小值.
取CE中点F,连接DF.∵等边△ABC的边长为6,AE=2,∴CE=AC﹣AE=6﹣2=4,
∴CF=EF=AE=2,又∵AD是BC边上的中线,∴DF是△BCE的中位线,∴BE=2DF,BE∥DF,
又∵E为AF的中点,∴M为AD的中点,∴ME是△ADF的中位线,∴DF=2ME,∴BE=2DF=4ME,
∴BM=BE﹣ME=4ME﹣ME=3ME,∴BE=BM.
在直角△BDM中,BD=BC=3,DM=AD=,∴BM==,∴BE=.
∵EM+CM=BE∴EM+CM的最小值为2.故选C.
二.填空题(共6小题)
10. 40° .
【解答】解:∵△ABC和△BDE都是等边三角形∴∠ABC=∠EBD=60°
∴∠ABE+∠EBC=∠EBC+∠CBD∴∠ABE=∠CBD=40°即∠CBD=40°,故答案为:40°.
11. 15 °.
【解答】解:∵△ABC是等边三角形,∴∠ACB=60°,∠ACD=120°,∵CG=CD,
∴∠CDG=30°,∠FDE=150°,∵DF=DE,∴∠EFD=15°.故答案为:15.
12. ①②③.
【解答】解:∵△ABC是等边三角形,∴AB=AC,∵AD是∠BAC的平分线,∴AD⊥BC,BD=DC,
∴∠ADC=90°,∵△ABC和△ADE是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,∴∠BAE=∠DAC,在△BAE和△CAD中,
,∴△BAE≌△CAD(SAS),∴∠DAC=∠BAE,BE=DC,∵BD=DC,
∴BE=BD,∵△ABC是等边三角形,∴∠BAC=60°,∵AD是∠BAC的平分线,
∴∠DAC=30°,∴∠BAE=30°,∵△ADE是等边三角形,∴∠DAE=60°,∴∠BAD=30°=∠BAE,
∵AE=AD,∴EF=DF.故答案为:①②③.
13. 6 .
【解答】解:作EG⊥OA于G,∵∠AOE=∠BOE,EC⊥OB,EG⊥OA,∴EG=EC=3,
∵EF∥OB,∴∠OEF=∠BOE=15°,∴∠EFG=30°,∴EF=2EC=6,故答案为:6.
14. 6 .
【解答】解:∵△ABC中,∠BAC=90°,∠B=30°,∴∠ACB=60°.
又∵CE是∠ACB的平分线,∴∠ECB=30°,∴∠AEC=∠B+∠ECB=60°,∠B=∠ECB
∴∠AEP=60°,BE=EC.又AD⊥BC,∴∠BAD=∠EAP=60°,则∠AEP=∠EAP=60°,
∴△AEP的等边三角形,则AE=AP=2,在直角△AEC中,∠ACE=30°,则EC=2AE=4,
∴BE=EC=4,∴AB=BE+AE=6.故答案是:6.
15. 5 m.
【解答】解:∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,∵DE⊥AB,DF⊥AC,垂足为E,F,
∴DE=BD,DF=DC,∴DE+DF=BD+DC=(BD+DC)BC.∴DE+DF=BC=×10=5cm.
三.解答题(共7小题)
16.【解答】解:(1)∵△ABC为等边三角形,∴∠BAC=∠C=60°,AB=AC.
在△ABE和△CAD中,,∴△ABE≌△CAD(SAS);
(2)∵△ABE≌△CAD,∴∠ABE=∠CAD.∵∠BFD=∠ABE+∠BAD,
∴∠BFD=∠BAD+∠CAD=∠BAC=60°.
答:∠BFD的度数为60°.
17.【解答】(1)证明:∵AB=AC,∠CAD=30°,AD⊥AB,∴∠BAC=120°,
∴∠B=∠C=∠CAD=30°,∴AD=CD,∴BD=2AD=2CD;
(2)解:如图,∵点E是BD的中点,∠BAD=90°,∴AE=BE=DE,
∵∠B=30°,∴∠ADE=60°,∴△ADE是等边三角形.
18【解答】解:(1)如图1所示,连接AB,作AB的垂直平分线与EF的交点P,即是自来水厂的位置;
(2)如图2所示,作点A关于直线l的对称点A′,连接A′B,则A′B与EF的交点Q到A、B两点的距离和最小,此处厂部到A,B村的水管最省料.21·cn·jy·com
19.【解答】解:有危险,理由如下:
过点P作PD⊥AB,交AB的延长线于点D,如图所示:
∵由题意可知:∠A=15°,∠PBD=30°,∴∠BPA=∠PBD﹣∠A=15°,即∠BPA=∠A,
∴PB=AB=15×2=30(海里),在Rt△BPD中,∠PBD=30°,PB=30海里,
∴PD=PB=15海里<18海里,则轮船不改变方向仍继续向前航行有触礁的危险.
20.【解答】证明:(1)∵∠ACB=90°,CD,CE三等分∠ACB,
∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,∵CD⊥AB,∴∠B=60°,∴∠A=30°,∴BC=AB,
即:AB=2BC;
(2)由(1)可知:∠A=∠ACE=30°,∠ECB=∠B=60°,
∴AE=CE,CE=BE,∴AE=CE=BE.
21【解答】解:(1)AF=BE.证明:在△AFC和△BEC中,
∵△ABC和△CEF是等边三角形,∴AC=BC,CF=CE,∠ACF=∠BCE=60°,
在△AFC与△BEC中,,∴△AFC≌△BEC(SAS),∴AF=BE.
(2)成立.理由:在△AFC和△BEC中,∵△ABC和△CEF是等边三角形,
∴AC=BC,CF=CE,∠ACB=∠FCE=60度,∴∠ACB﹣∠FCB=∠FCE﹣∠FCB,
即∠ACF=∠BCE,
在△AFC与△BEC中,,∴△AFC≌△BEC(SAS),∴AF=BE.
22.【解答】证明:(1)∵BF=AC,AB=AE(已知)∴FA=EC(等量加等量和相等).
∵△DEF是等边三角形(已知),∴EF=DE(等边三角形的性质).
又∵AE=CD(已知),在△AEF与△CDE中,∴△AEF≌△CDE(SSS).
(2)是等边三角形,理由如下:
由△AEF≌△CDE,得∠FEA=∠EDC(对应角相等),
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF(等量代换),
△DEF是等边三角形(已知),∴∠DEF=60°(等边三角形的性质),
∴∠BCA=60°(等量代换),由△AEF≌△CDE,得∠EFA=∠DEC,∵∠DEC+∠FEC=60°,
∴∠EFA+∠FEC=60°,又∠BAC是△AEF的外角,∴∠BAC=∠EFA+∠FEC=60°,
∴△ABC中,AB=BC(等角对等边).∴△ABC是等边三角形(等边三角形的判定).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
八上数学第十三章培优提高 等边三角形
一.选择题(共9小题)
1.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
2.已知∠AOB=30°,点P在∠AOB的内部,点C与点P关于OB对称,点D与点P关于OA对称,则△OCD是( )21世纪教育网版权所有
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
3.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )www.21-cn-jy.com
A.6cm B.5cm C.4cm D.3cm
4.如图,在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD,AD=2,则BC等于( )
A.4 B.5 C.6 D.8
5.如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )2·1·c·n·j·y
A.△ACE≌△BCD B.△BGC≌△AFC C.△ADB≌△CEA D.△DCG≌△ECF
第3题图 第4题图 第5题图
6.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )
A.3cm B.4cm C.4.5cm D.5cm
7.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( )
A.2cm B.4cm C.8cm D.16cm
8.如图,已知△ABC和△CDE都是等边三角形,AD、BE交于点F,则∠AFB等于( )
A.50° B.60° C.45° D.∠BCD
9.如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
A. B. C. D.
第6题图 第8题图 第9题图
二.填空题(共6小题)
10.如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为 .
11.如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠EFD= °.21·世纪*教育网
12.如图,△ABC、△ADE均为等边三角形,AD平分∠BAC交BC于D,DE交AB于F,则下列结论:①AD⊥BC;②EF=FD; ③BE=BD,其中正确的有 (填序号).
第10题图 第11题图 第12题图
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=3,则EF的长为 .
14.如图,△ABC中,∠BAC=90°,∠B=30°,AD⊥BC于D,CE是∠ACB的平分线,且交AD于P点.如果AP=2,则AB的长为 .2-1-c-n-j-y
15.如图是屋顶的“人字形“钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为中柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF= m.
第13题图 第14题图 第15题图
三.解答题(共7小题)
16.如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.www-2-1-cnjy-com
(1)证明:△ABE≌△CAD;
(2)求∠BFD的度数.
17.如图,在△ABC中,AB=AC,AD⊥AB交BC于点D,∠CAD=30°.
(1)求证:BD=2CD;
(2)取BD的中点E,连接AE,求证:△ADE为等边三角形.
18.如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.
(1)求作点P,使P到A、B两村的距离相等.(不写作法,保留作图痕迹)
(2)求作点Q,使Q到A、B两村的水管最省料.(不写作法,保留作图痕迹)
19.如图,一艘轮船以15海里/时的速度由南向北航行,在A处测得小岛P在北偏西15°方向上,两小时后,轮船在B处测得小岛P在北偏西30°方向上.在小岛周围18海里内有暗礁,若轮船不改变方向仍继续向前航行,问:有无触礁的危险?并说明你的理由.
20.如图,在△ABC,∠ACB=90°,CD、CE三等分∠ACB,CD⊥AB,
求证:(1)AB=2BC;(2)CE=AE=EB.
21.如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE
(1)线段AF和BE有怎样的大小关系?请证明你的结论;
(2)将图a中的△CEF绕点C旋转一定的角度,得到图b,(1)中的结论还成立吗?作出判断并说明理由.21教育网
22.如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接点D、E、F,得到△DEF为等边三角形.21cnjy.com
(1)试说明△AEF≌△CDE;
(2)△ABC是等边三角形吗?请说明你的理由.
参考答案与试题解析
一.选择题(共9小题)
1D.【解答】解:①两个角为60度,则第三个角也是60度,则其是等边三角形,故正确;
②这是等边三角形的判定2,故正确;③三个外角相等则三个内角相等,则其是等边三角形,故正确;④根据等边三角形三线合一性质,故正确.所以都正确.故选D.
2B.【解答】解:∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为D、C,
∴OP=OD=OC且∠DOC=2∠AOB=60°,∴△OCD是等边三角形.故选B.
3D.【解答】解:∵在△ABC中,∠ACB=90°,∠B=15°,∴∠BAC=90°﹣15°=75°,
∵DE垂直平分AB,交BC于点E,BE=6cm,∴BE=AE=6cm,∴∠EAB=∠B=15°,
∴∠EAC=75°﹣15°=60°,∵∠C=90°,∴∠AEC=30°,∴AC=AE=6cm=3cm,
故选D.
4C.【解答】解:∵AB=AC,∠C=30°,∴∠B=∠C=30°,∠BAC=120°,
∵AB⊥AD,∴∠BAD=90°,∵AD=2,∴BD=2AD=4,∵∠DAC=120°﹣90°=30°,
∴∠DAC=∠C,∴AD=DC=2,∴BC=BD+DC=4+2=6,故选C.
5C.【解答】解:∵△ABC和△CDE都是等边三角形,∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACD=∠ECD+∠ACD,即∠BCD=∠ACE,
∴在△BCD和△ACE中 ,∴△BCD≌△ACE(SAS),故A成立,
∴∠DBC=∠CAE,∵∠BCA=∠ECD=60°,∴∠ACD=60°,
在△BGC和△AFC中,∴△BGC≌△AFC,故B成立,
∵△BCD≌△ACE,∴∠CDB=∠CEA,
在△DCG和△ECF中,∴△DCG≌△ECF,故D成立,故选:C.
6A.【解答】解:由折叠可得AD=A′D;AE=A′E,∴阴影部分图形的周长为AB+BC+AC=3cm.
7C.【解答】解:在Rt△ABC中,CD是斜边AB上的高∴∠B+∠A=∠DCA+∠A=90°
∴∠DCA=∠B=30°∴AC=2AD=4,∴AB=2AC=8cm.故选C.
8B.【解答】解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,
在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE,
设AD与BC相交于P点,在△ACP和△BFP中,有一对对顶角,∴∠AFB=∠ACB=60°
9C.【解答】解:连接BE,与AD交于点M.则BE就是EM+CM的最小值.
取CE中点F,连接DF.∵等边△ABC的边长为6,AE=2,∴CE=AC﹣AE=6﹣2=4,
∴CF=EF=AE=2,又∵AD是BC边上的中线,∴DF是△BCE的中位线,∴BE=2DF,BE∥DF,
又∵E为AF的中点,∴M为AD的中点,∴ME是△ADF的中位线,∴DF=2ME,∴BE=2DF=4ME,
∴BM=BE﹣ME=4ME﹣ME=3ME,∴BE=BM.
在直角△BDM中,BD=BC=3,DM=AD=,∴BM==,∴BE=.
∵EM+CM=BE∴EM+CM的最小值为2.故选C.
二.填空题(共6小题)
10. 40° .
【解答】解:∵△ABC和△BDE都是等边三角形∴∠ABC=∠EBD=60°
∴∠ABE+∠EBC=∠EBC+∠CBD∴∠ABE=∠CBD=40°即∠CBD=40°,故答案为:40°.
11. 15 °.
【解答】解:∵△ABC是等边三角形,∴∠ACB=60°,∠ACD=120°,∵CG=CD,
∴∠CDG=30°,∠FDE=150°,∵DF=DE,∴∠EFD=15°.故答案为:15.
12. ①②③.
【解答】解:∵△ABC是等边三角形,∴AB=AC,∵AD是∠BAC的平分线,∴AD⊥BC,BD=DC,
∴∠ADC=90°,∵△ABC和△ADE是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,∴∠BAE=∠DAC,在△BAE和△CAD中,
,∴△BAE≌△CAD(SAS),∴∠DAC=∠BAE,BE=DC,∵BD=DC,
∴BE=BD,∵△ABC是等边三角形,∴∠BAC=60°,∵AD是∠BAC的平分线,
∴∠DAC=30°,∴∠BAE=30°,∵△ADE是等边三角形,∴∠DAE=60°,∴∠BAD=30°=∠BAE,
∵AE=AD,∴EF=DF.故答案为:①②③.
13. 6 .
【解答】解:作EG⊥OA于G,∵∠AOE=∠BOE,EC⊥OB,EG⊥OA,∴EG=EC=3,
∵EF∥OB,∴∠OEF=∠BOE=15°,∴∠EFG=30°,∴EF=2EC=6,故答案为:6.
14. 6 .
【解答】解:∵△ABC中,∠BAC=90°,∠B=30°,∴∠ACB=60°.
又∵CE是∠ACB的平分线,∴∠ECB=30°,∴∠AEC=∠B+∠ECB=60°,∠B=∠ECB
∴∠AEP=60°,BE=EC.又AD⊥BC,∴∠BAD=∠EAP=60°,则∠AEP=∠EAP=60°,
∴△AEP的等边三角形,则AE=AP=2,在直角△AEC中,∠ACE=30°,则EC=2AE=4,
∴BE=EC=4,∴AB=BE+AE=6.故答案是:6.
15. 5 m.
【解答】解:∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,∵DE⊥AB,DF⊥AC,垂足为E,F,
∴DE=BD,DF=DC,∴DE+DF=BD+DC=(BD+DC)BC.∴DE+DF=BC=×10=5cm.
三.解答题(共7小题)
16.【解答】解:(1)∵△ABC为等边三角形,∴∠BAC=∠C=60°,AB=AC.
在△ABE和△CAD中,,∴△ABE≌△CAD(SAS);
(2)∵△ABE≌△CAD,∴∠ABE=∠CAD.∵∠BFD=∠ABE+∠BAD,
∴∠BFD=∠BAD+∠CAD=∠BAC=60°.
答:∠BFD的度数为60°.
17.【解答】(1)证明:∵AB=AC,∠CAD=30°,AD⊥AB,∴∠BAC=120°,
∴∠B=∠C=∠CAD=30°,∴AD=CD,∴BD=2AD=2CD;
(2)解:如图,∵点E是BD的中点,∠BAD=90°,∴AE=BE=DE,
∵∠B=30°,∴∠ADE=60°,∴△ADE是等边三角形.
18【解答】解:(1)如图1所示,连接AB,作AB的垂直平分线与EF的交点P,即是自来水厂的位置;
(2)如图2所示,作点A关于直线l的对称点A′,连接A′B,则A′B与EF的交点Q到A、B两点的距离和最小,此处厂部到A,B村的水管最省料.21·cn·jy·com
19.【解答】解:有危险,理由如下:
过点P作PD⊥AB,交AB的延长线于点D,如图所示:
∵由题意可知:∠A=15°,∠PBD=30°,∴∠BPA=∠PBD﹣∠A=15°,即∠BPA=∠A,
∴PB=AB=15×2=30(海里),在Rt△BPD中,∠PBD=30°,PB=30海里,
∴PD=PB=15海里<18海里,则轮船不改变方向仍继续向前航行有触礁的危险.
20.【解答】证明:(1)∵∠ACB=90°,CD,CE三等分∠ACB,
∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,∵CD⊥AB,∴∠B=60°,∴∠A=30°,∴BC=AB,
即:AB=2BC;
(2)由(1)可知:∠A=∠ACE=30°,∠ECB=∠B=60°,
∴AE=CE,CE=BE,∴AE=CE=BE.
21【解答】解:(1)AF=BE.证明:在△AFC和△BEC中,
∵△ABC和△CEF是等边三角形,∴AC=BC,CF=CE,∠ACF=∠BCE=60°,
在△AFC与△BEC中,,∴△AFC≌△BEC(SAS),∴AF=BE.
(2)成立.理由:在△AFC和△BEC中,∵△ABC和△CEF是等边三角形,
∴AC=BC,CF=CE,∠ACB=∠FCE=60度,∴∠ACB﹣∠FCB=∠FCE﹣∠FCB,
即∠ACF=∠BCE,
在△AFC与△BEC中,,∴△AFC≌△BEC(SAS),∴AF=BE.
22.【解答】证明:(1)∵BF=AC,AB=AE(已知)∴FA=EC(等量加等量和相等).
∵△DEF是等边三角形(已知),∴EF=DE(等边三角形的性质).
又∵AE=CD(已知),在△AEF与△CDE中,∴△AEF≌△CDE(SSS).
(2)是等边三角形,理由如下:
由△AEF≌△CDE,得∠FEA=∠EDC(对应角相等),
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF(等量代换),
△DEF是等边三角形(已知),∴∠DEF=60°(等边三角形的性质),
∴∠BCA=60°(等量代换),由△AEF≌△CDE,得∠EFA=∠DEC,∵∠DEC+∠FEC=60°,
∴∠EFA+∠FEC=60°,又∠BAC是△AEF的外角,∴∠BAC=∠EFA+∠FEC=60°,
∴△ABC中,AB=BC(等角对等边).∴△ABC是等边三角形(等边三角形的判定).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
