新疆伊犁州伊宁市2016-2017学年上学期八年级期中数学试题含解析
文档属性
| 名称 | 新疆伊犁州伊宁市2016-2017学年上学期八年级期中数学试题含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 334.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-12 00:00:00 | ||
图片预览


文档简介
2016-2017学年新疆伊犁州伊宁八年级(上)期中数学考试卷
一、选择题
1、在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是(
)
A、
B、
C、
D、
2、点(﹣3,2)关于x轴的对称点是(
)
A、(﹣3,﹣2)
B、(3,2)
C、(﹣3,2)
D、(3,﹣2)
3、以下各组线段为边,能组成三角形的是(
)
A、2cm,4cm,6cm
B、8cm,6cm,4cm
C、14cm,6cm,7cm
D、2cm,3cm,6cm
4、如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是(
)
A、∠B=∠C
B、AD⊥BC
C、AD平分∠BAC
D、AB=2BD
5、等腰三角形的一个角是70°,则它的底角是(
)
A、70°
B、70°或55°
C、80°和100°
D、110°
6、如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=(
)
A、90°
B、135°
C、270°
D、315°
7、下列命题中,正确的是(
)
A、三角形的一个外角大于任何一个内角
B、三角形的一条中线将三角形分成两个面积相等的三角形
C、两边和其中一边的对角分别相等的两个三角形全等
D、三角形的三条高都在三角形内部
8、∠AOB的平分线上一点P到OA的距离为5,Q是OB上任一点,则(
)
A、PQ>5
B、PQ≥5
C、PQ<5
D、PQ≤5
9、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是(
)
A、带①去
B、带②去
C、带③去
D、带①和②去
10、如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于G.则下列结论中错误的是(
)
A、AD=BE
B、BE⊥AC
C、△CFG为等边三角形
D、FG∥BC
二、填空题
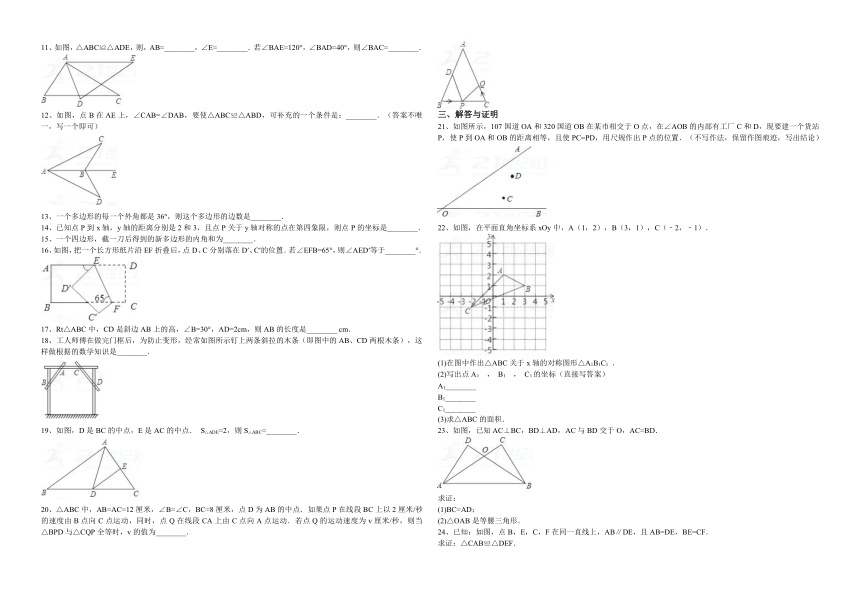
11、如图,△ABC≌△ADE,则,AB=________,∠E=________.若∠BAE=120°,∠BAD=40°,则∠BAC=________.
12、如图,点B在AE上,∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是:________.(答案不唯一,写一个即可)
13、一个多边形的每一个外角都是36°,则这个多边形的边数是________.
14、已知点P到x轴,y轴的距离分别是2和3,且点P关于y轴对称的点在第四象限,则点P的坐标是________.
15、一个四边形,截一刀后得到的新多边形的内角和为________.
16、如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=65°,则∠AED′等于________°.
17、Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是________ cm.
18、工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB、CD两根木条),这样做根据的数学知识是________.
19、如图,D是BC的中点,E是AC的中点.
S△ADE=2,则S△ABC=________.
20、△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________.
三、解答与证明
21、如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
22、如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1
.
(2)写出点A1
,
B1
,
C1的坐标(直接写答案)
A1________
B1________
C1________
(3)求△ABC的面积.
23、如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:
(1)BC=AD;
(2)△OAB是等腰三角形.
24、已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:△CAB≌△DEF.
25、如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是________.
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
答案解析部分
一、>选择题
1、
【答案】A
【考点】轴对称图形
【解析】【解答】解:A、是轴对称图形,故A符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、不是轴对称图形,故D不符合题意.
故选:A.
【分析】根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
2、
【答案】A
【考点】关于x轴、y轴对称的点的坐标
【解析】【解答】解:点(﹣3,2)关于x轴的对称点的坐标是:(﹣3,﹣2).
故选A.
【分析】直接利用关于x轴对称点的性质,进而得出答案.
3、
【答案】B
【考点】三角形三边关系
【解析】【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选B.
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
4、
【答案】D
【考点】等腰三角形的性质
【解析】【解答】解:∵△ABC中,AB=AC,D是BC中点
∴∠B=∠C,(故A正确)
AD⊥BC,(故B正确)
∠BAD=∠CAD(故C正确)
无法得到AB=2BD,(故D不正确).
故选:D.
【分析】此题需对每一个选项进行验证从而求解.
5、
【答案】B
【考点】等腰三角形的性质
【解析】【解答】解:∵等腰三角形的一个角是70°,
∴当顶角为70°时,那么底角为:(180°﹣70°)÷2=55°,
当底角为70°时,那么顶角为:180°﹣70°﹣70°=40°,
故选B.
【分析】题中未指明已知的角是顶角还是底角,故应该分情况进行分析,从而求解.
6、
【答案】C
【考点】三角形内角和定理,多边形内角与外角
【解析】【解答】解:∵∠C=90°,
∴∠A+∠B=90°.
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣90°=270°.
故选:C.
【分析】先根据直角三角形的性质求得两个锐角和是90度,再根据四边形的内角和是360度,即可求得∠1+∠2的值.
7、
【答案】B
【考点】命题与定理
【解析】【解答】解:A、三角形的一个外角大于任何一个不相邻的一个内角,所以A选项错误;
B、三角形的一条中线将三角形分成两个面积相等的三角形,所以B选项正确;
C、两边和它们的夹角分别对应相等的两个三角形全等,所以C选项错误;
D、钝角三角形的高有两条在三角形外部,所以D选项错误.
故选B.
【分析】根据三角形外角性质对A进行判断;
根据三角形中线性质和三角形面积公式对B进行判断;
根据三角形全等的判定对C进行判断;
根据三角形高线定义对D进行判断.
8、
【答案】B
【考点】角平分线的性质
【解析】【解答】解:∠AOB的平分线上一点P到OA的距离为5
则P到OB的距离为5
因为Q是OB上任一点,则PQ≥5
故选B.
【分析】直线外一点与直线上各点连接的所有线段中,垂线段最短,和角平分线的性质计算.
9、
【答案】C
【考点】全等三角形的应用
【解析】【解答】解:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误;
B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误;
C、带③去,不但保留了原三角形的两个角还保留了其中一个边,符合ASA判定,故C选项正确;
D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D选项错误.
故选:C.
【分析】此题可以采用全等三角形的判定方法以及排除法进行分析,从而确定最后的答案.
10、
【答案】B
【考点】全等三角形的判定与性质,等边三角形的性质
【解析】【解答】解:A、∵△ABC和△CDE均为等边三角形,
∴AC=BC,EC=DC,
∠ACB﹦∠ECD=60°,
∴∠ACD﹦∠ECB,
在△ACD与△BCE中,
∵
,
∴△ACD≌△BCE(SAS),
∴AD=BE,正确,故本选项错误;
B、根据已知不能推出F是AC中点,即AC和BF不垂直,所以AC⊥BE错误,故本选项正确;
C、△CFG是等边三角形,理由如下:
∵∠ACG=180°﹣60°﹣60°=60°=∠BCA,
∵△ACD≌△BCE,
∴∠CBE=∠CAD,
在△ACG和△BCF中
∵
,
∴△ACG≌△BCF(ASA),
∴CG=CH,
又∵∠ACG=60°
∴△CGH是等边三角形,正确,故本选项错误;
D、∵△CFG是等边三角形,
∴∠CFG﹦60°=∠ACB,
∴FG∥BC,正确,故本选项错误;
故选B.
【分析】A、证明△ACD≌△BCE即可得出答案;
B、根据等边三角形性质得出AB=BC,只有F为AC中点时,才能推出AC⊥BE.
C、由△ACG≌△BCF,推出CG=CF,根据∠ACG=60°即可证明;
D、根据等边三角形性质得出∠CFG﹦∠ACB=60°,根据平行线的判定推出即可.
二、>填空题
11、
【答案】AB;∠C;80°
【考点】全等三角形的性质
【解析】【解答】解:∵△ABC≌△ADE,
∴AB=AD,∠E=∠C,∠BAC=∠DAE;
∵∠DAC是公共角
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
已知∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,∠BAC=∠BAE﹣∠CAE=120°﹣40°=80°.
故答案分别填:AB、∠C、80°.
【分析】根据△ABC≌△ADE,可得其对应边对应角相等,即可得AB=AD,∠E=∠C,∠BAC=∠DAE;由∠DAC是公共角易证得∠BAD=∠CAE,已知∠BAE=120°,∠BAD=40°,即可求得∠BAC的度数.
12、
【答案】∠CBE=∠DBE(ASA)
【考点】全等三角形的判定
【解析】【解答】解:根据判定方法,可填AC=AD(SAS);或∠CBA=∠DBA(ASA);或∠C=∠D(AAS);∠CBE=∠DBE(ASA).
【分析】△ABC和△ABD已经满足一条边相等(公共边AB)和一对对应角相等(∠CAB=∠DAB),只要再添加一边(SAS)或一角(ASA、AAS)即可得出结论.
13、
【答案】10
【考点】多边形内角与外角
【解析】【解答】解:∵一个多边形的每个外角都等于36°,
∴多边形的边数为360°÷36°=10.
故答案为:10.
【分析】多边形的外角和是固定的360°,依此可以求出多边形的边数.
14、
【答案】(﹣3,﹣2)
【考点】关于x轴、y轴对称的点的坐标
【解析】【解答】解:因为点P关于y轴对称的点在第四象限,所以点P在第3象限,点P的坐标是(﹣3,﹣2).
【分析】横坐标的绝对值是点到y轴的距离,纵坐标的绝对值是点到x轴的距离.关于y轴对称的点,纵坐标相同,横坐标互为相反数.
15、
【答案】180°或360°或540°
【考点】多边形内角与外角
【解析】【解答】解:∵一个四边形截一刀后得到的多边形可能是三角形,可能是四边形,也可能是五边形,
∴内角和为180°或360°或540°.
故答案为:180°或360°或540°.
【分析】根据一个四边形截一刀后得到的多边形的边数即可得出结果.
16、
【答案】50
【考点】翻折变换(折叠问题)
【解析】【解答】解:∵AD∥BC,
∴∠EFB=∠FED=65°,
由折叠的性质知,∠DEF=∠FED′=65°,
∴∠AED′=180°﹣2∠FED=50°.
故∠AED′等于50°.
【分析】首先根据AD∥BC,求出∠FED的度数,然后根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,则可知∠DEF=∠FED′,最后求得∠AED′的大小.
17、
【答案】8
【考点】含30度角的直角三角形
【解析】【解答】解:在Rt△ABC中,
∵CD是斜边AB上的高,
∴∠ADC=90°,
∴∠ACD=∠B=30°(同角的余角相等),
∵AD=2cm,
在Rt△ACD中,AC=2AD=4cm,
在Rt△ABC中,AB=2AC=8cm.
∴AB的长度是8cm.
【分析】先求出∠ACD=30°,然后根据30°所对的直角边等于斜边的一半解答.
18、
【答案】三角形的稳定性
【考点】三角形的稳定性
【解析】【解答】解:这样做根据的数学知识是:三角形的稳定性.
【分析】钉上两条斜拉的木条后,形成了两个三角形,故这种做法根据的是三角形的稳定性.
19、
【答案】8
【考点】三角形的面积
【解析】【解答】解:∵E是AC的中点,
∴S△ACD=2S△ADE=2×2=4,
∵D是BC的中点,
∴S△ABC=2S△ACD=2×4=8.
故答案为:8.
【分析】根据三角形的中线将三角形分成面积相等的两个三角形先求出△ACD的面积,再求解即可.
20、
【答案】2或3
【考点】全等三角形的判定
【解析】【解答】解:当BD=PC时,△BPD与△CQP全等,
∵点D为AB的中点,
∴BD=
AB=6cm,
∵BD=PC,
∴BP=8﹣6=2(cm),
∵点P在线段BC上以2厘米/秒的速度由B点向C点运动,
∴运动时间时1s,
∵△DBP≌△PCQ,
∴BP=CQ=2cm,
∴v=2÷1=2;
当BD=CQ时,△BDP≌△QCP,
∵BD=6cm,PB=PC,
∴QC=6cm,
∵BC=8cm,
∴BP=4cm,
∴运动时间为4÷2=2(s),
∴v=6÷2=3(m/s),
故答案为:2或3.
【分析】此题要分两种情况:①当BD=PC时,△BPD与△CQP全等,计算出BP的长,进而可得运动时间,然后再求v;②当BD=CQ时,△BDP≌△QCP,计算出BP的长,进而可得运动时间,然后再求v.
三、>解答与证明
21、
【答案】解:如图:
【考点】作图—尺规作图的定义,作图—基本作图
【解析】【分析】做出CD的垂直平分线和∠AOB的平分线,其交点P或P′即为所求.
22、
【答案】
(1)解:如图,△A1B1C1即为所求
(2)(1,﹣2);(3,﹣1);(﹣2,1)
(3)解:S△ABC=5×3﹣1\2×3×3﹣1\2×2×1﹣1\2×5×2
=15﹣4.5﹣1﹣5
=4.5
【考点】作图-轴对称变换
【解析】【解答】解:(2)由图可知,A1
(1,﹣2),B1
(3,﹣1),C1
(﹣2,1).
故答案为:(1,﹣2),(3,﹣1),(﹣2,1);
【分析】(1)分别作出各点关于x轴的对称点,再顺次连接即可;(2)根据各点在坐标系中的位置写出各点坐标即可;(3)利用矩形的面积减去三个顶点上三角形的面积即可.
23、
【答案】
(1)证明:∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
∵
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD
(2)证明:∵Rt△ABC≌Rt△BAD,
∴∠CAB=∠DBA,
∴OA=OB,
∴△OAB是等腰三角形
【考点】全等三角形的判定与性质,等腰三角形的判定
【解析】【分析】(1)根据AC⊥BC,BD⊥AD,得出△ABC与△BAD是直角三角形,再根据AC=BD,AB=BA,得出Rt△ABC≌Rt△BAD,即可证出BC=AD,(2)根据Rt△ABC≌Rt△BAD,得出∠CAB=∠DBA,从而证出OA=OB,△OAB是等腰三角形.
24、
【答案】证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF
∴BE+EC=CF+EC
即BC=EF
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS)
【考点】全等三角形的判定
【解析】【分析】根据BE=CF得到BC=EF,然后利用SAS判定定理证明△ABC≌△DEF即可.
25、
【答案】
(1)50°
(2)解:猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
如图:
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
【考点】线段垂直平分线的性质,等腰三角形的性质,轴对称-最短路线问题
【解析】【解答】解:(1)若∠B=70°,则∠NMA的度数是
50°,
故答案为:50°;
【分析】(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;(2)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;(3)根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
一、选择题
1、在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是(
)
A、
B、
C、
D、
2、点(﹣3,2)关于x轴的对称点是(
)
A、(﹣3,﹣2)
B、(3,2)
C、(﹣3,2)
D、(3,﹣2)
3、以下各组线段为边,能组成三角形的是(
)
A、2cm,4cm,6cm
B、8cm,6cm,4cm
C、14cm,6cm,7cm
D、2cm,3cm,6cm
4、如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是(
)
A、∠B=∠C
B、AD⊥BC
C、AD平分∠BAC
D、AB=2BD
5、等腰三角形的一个角是70°,则它的底角是(
)
A、70°
B、70°或55°
C、80°和100°
D、110°
6、如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=(
)
A、90°
B、135°
C、270°
D、315°
7、下列命题中,正确的是(
)
A、三角形的一个外角大于任何一个内角
B、三角形的一条中线将三角形分成两个面积相等的三角形
C、两边和其中一边的对角分别相等的两个三角形全等
D、三角形的三条高都在三角形内部
8、∠AOB的平分线上一点P到OA的距离为5,Q是OB上任一点,则(
)
A、PQ>5
B、PQ≥5
C、PQ<5
D、PQ≤5
9、如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是(
)
A、带①去
B、带②去
C、带③去
D、带①和②去
10、如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于G.则下列结论中错误的是(
)
A、AD=BE
B、BE⊥AC
C、△CFG为等边三角形
D、FG∥BC
二、填空题
11、如图,△ABC≌△ADE,则,AB=________,∠E=________.若∠BAE=120°,∠BAD=40°,则∠BAC=________.
12、如图,点B在AE上,∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是:________.(答案不唯一,写一个即可)
13、一个多边形的每一个外角都是36°,则这个多边形的边数是________.
14、已知点P到x轴,y轴的距离分别是2和3,且点P关于y轴对称的点在第四象限,则点P的坐标是________.
15、一个四边形,截一刀后得到的新多边形的内角和为________.
16、如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=65°,则∠AED′等于________°.
17、Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是________ cm.
18、工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB、CD两根木条),这样做根据的数学知识是________.
19、如图,D是BC的中点,E是AC的中点.
S△ADE=2,则S△ABC=________.
20、△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________.
三、解答与证明
21、如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
22、如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1
.
(2)写出点A1
,
B1
,
C1的坐标(直接写答案)
A1________
B1________
C1________
(3)求△ABC的面积.
23、如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:
(1)BC=AD;
(2)△OAB是等腰三角形.
24、已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:△CAB≌△DEF.
25、如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是________.
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
答案解析部分
一、
1、
【答案】A
【考点】轴对称图形
【解析】【解答】解:A、是轴对称图形,故A符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、不是轴对称图形,故D不符合题意.
故选:A.
【分析】根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
2、
【答案】A
【考点】关于x轴、y轴对称的点的坐标
【解析】【解答】解:点(﹣3,2)关于x轴的对称点的坐标是:(﹣3,﹣2).
故选A.
【分析】直接利用关于x轴对称点的性质,进而得出答案.
3、
【答案】B
【考点】三角形三边关系
【解析】【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选B.
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
4、
【答案】D
【考点】等腰三角形的性质
【解析】【解答】解:∵△ABC中,AB=AC,D是BC中点
∴∠B=∠C,(故A正确)
AD⊥BC,(故B正确)
∠BAD=∠CAD(故C正确)
无法得到AB=2BD,(故D不正确).
故选:D.
【分析】此题需对每一个选项进行验证从而求解.
5、
【答案】B
【考点】等腰三角形的性质
【解析】【解答】解:∵等腰三角形的一个角是70°,
∴当顶角为70°时,那么底角为:(180°﹣70°)÷2=55°,
当底角为70°时,那么顶角为:180°﹣70°﹣70°=40°,
故选B.
【分析】题中未指明已知的角是顶角还是底角,故应该分情况进行分析,从而求解.
6、
【答案】C
【考点】三角形内角和定理,多边形内角与外角
【解析】【解答】解:∵∠C=90°,
∴∠A+∠B=90°.
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣90°=270°.
故选:C.
【分析】先根据直角三角形的性质求得两个锐角和是90度,再根据四边形的内角和是360度,即可求得∠1+∠2的值.
7、
【答案】B
【考点】命题与定理
【解析】【解答】解:A、三角形的一个外角大于任何一个不相邻的一个内角,所以A选项错误;
B、三角形的一条中线将三角形分成两个面积相等的三角形,所以B选项正确;
C、两边和它们的夹角分别对应相等的两个三角形全等,所以C选项错误;
D、钝角三角形的高有两条在三角形外部,所以D选项错误.
故选B.
【分析】根据三角形外角性质对A进行判断;
根据三角形中线性质和三角形面积公式对B进行判断;
根据三角形全等的判定对C进行判断;
根据三角形高线定义对D进行判断.
8、
【答案】B
【考点】角平分线的性质
【解析】【解答】解:∠AOB的平分线上一点P到OA的距离为5
则P到OB的距离为5
因为Q是OB上任一点,则PQ≥5
故选B.
【分析】直线外一点与直线上各点连接的所有线段中,垂线段最短,和角平分线的性质计算.
9、
【答案】C
【考点】全等三角形的应用
【解析】【解答】解:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误;
B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误;
C、带③去,不但保留了原三角形的两个角还保留了其中一个边,符合ASA判定,故C选项正确;
D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D选项错误.
故选:C.
【分析】此题可以采用全等三角形的判定方法以及排除法进行分析,从而确定最后的答案.
10、
【答案】B
【考点】全等三角形的判定与性质,等边三角形的性质
【解析】【解答】解:A、∵△ABC和△CDE均为等边三角形,
∴AC=BC,EC=DC,
∠ACB﹦∠ECD=60°,
∴∠ACD﹦∠ECB,
在△ACD与△BCE中,
∵
,
∴△ACD≌△BCE(SAS),
∴AD=BE,正确,故本选项错误;
B、根据已知不能推出F是AC中点,即AC和BF不垂直,所以AC⊥BE错误,故本选项正确;
C、△CFG是等边三角形,理由如下:
∵∠ACG=180°﹣60°﹣60°=60°=∠BCA,
∵△ACD≌△BCE,
∴∠CBE=∠CAD,
在△ACG和△BCF中
∵
,
∴△ACG≌△BCF(ASA),
∴CG=CH,
又∵∠ACG=60°
∴△CGH是等边三角形,正确,故本选项错误;
D、∵△CFG是等边三角形,
∴∠CFG﹦60°=∠ACB,
∴FG∥BC,正确,故本选项错误;
故选B.
【分析】A、证明△ACD≌△BCE即可得出答案;
B、根据等边三角形性质得出AB=BC,只有F为AC中点时,才能推出AC⊥BE.
C、由△ACG≌△BCF,推出CG=CF,根据∠ACG=60°即可证明;
D、根据等边三角形性质得出∠CFG﹦∠ACB=60°,根据平行线的判定推出即可.
二、
11、
【答案】AB;∠C;80°
【考点】全等三角形的性质
【解析】【解答】解:∵△ABC≌△ADE,
∴AB=AD,∠E=∠C,∠BAC=∠DAE;
∵∠DAC是公共角
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
已知∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,∠BAC=∠BAE﹣∠CAE=120°﹣40°=80°.
故答案分别填:AB、∠C、80°.
【分析】根据△ABC≌△ADE,可得其对应边对应角相等,即可得AB=AD,∠E=∠C,∠BAC=∠DAE;由∠DAC是公共角易证得∠BAD=∠CAE,已知∠BAE=120°,∠BAD=40°,即可求得∠BAC的度数.
12、
【答案】∠CBE=∠DBE(ASA)
【考点】全等三角形的判定
【解析】【解答】解:根据判定方法,可填AC=AD(SAS);或∠CBA=∠DBA(ASA);或∠C=∠D(AAS);∠CBE=∠DBE(ASA).
【分析】△ABC和△ABD已经满足一条边相等(公共边AB)和一对对应角相等(∠CAB=∠DAB),只要再添加一边(SAS)或一角(ASA、AAS)即可得出结论.
13、
【答案】10
【考点】多边形内角与外角
【解析】【解答】解:∵一个多边形的每个外角都等于36°,
∴多边形的边数为360°÷36°=10.
故答案为:10.
【分析】多边形的外角和是固定的360°,依此可以求出多边形的边数.
14、
【答案】(﹣3,﹣2)
【考点】关于x轴、y轴对称的点的坐标
【解析】【解答】解:因为点P关于y轴对称的点在第四象限,所以点P在第3象限,点P的坐标是(﹣3,﹣2).
【分析】横坐标的绝对值是点到y轴的距离,纵坐标的绝对值是点到x轴的距离.关于y轴对称的点,纵坐标相同,横坐标互为相反数.
15、
【答案】180°或360°或540°
【考点】多边形内角与外角
【解析】【解答】解:∵一个四边形截一刀后得到的多边形可能是三角形,可能是四边形,也可能是五边形,
∴内角和为180°或360°或540°.
故答案为:180°或360°或540°.
【分析】根据一个四边形截一刀后得到的多边形的边数即可得出结果.
16、
【答案】50
【考点】翻折变换(折叠问题)
【解析】【解答】解:∵AD∥BC,
∴∠EFB=∠FED=65°,
由折叠的性质知,∠DEF=∠FED′=65°,
∴∠AED′=180°﹣2∠FED=50°.
故∠AED′等于50°.
【分析】首先根据AD∥BC,求出∠FED的度数,然后根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,则可知∠DEF=∠FED′,最后求得∠AED′的大小.
17、
【答案】8
【考点】含30度角的直角三角形
【解析】【解答】解:在Rt△ABC中,
∵CD是斜边AB上的高,
∴∠ADC=90°,
∴∠ACD=∠B=30°(同角的余角相等),
∵AD=2cm,
在Rt△ACD中,AC=2AD=4cm,
在Rt△ABC中,AB=2AC=8cm.
∴AB的长度是8cm.
【分析】先求出∠ACD=30°,然后根据30°所对的直角边等于斜边的一半解答.
18、
【答案】三角形的稳定性
【考点】三角形的稳定性
【解析】【解答】解:这样做根据的数学知识是:三角形的稳定性.
【分析】钉上两条斜拉的木条后,形成了两个三角形,故这种做法根据的是三角形的稳定性.
19、
【答案】8
【考点】三角形的面积
【解析】【解答】解:∵E是AC的中点,
∴S△ACD=2S△ADE=2×2=4,
∵D是BC的中点,
∴S△ABC=2S△ACD=2×4=8.
故答案为:8.
【分析】根据三角形的中线将三角形分成面积相等的两个三角形先求出△ACD的面积,再求解即可.
20、
【答案】2或3
【考点】全等三角形的判定
【解析】【解答】解:当BD=PC时,△BPD与△CQP全等,
∵点D为AB的中点,
∴BD=
AB=6cm,
∵BD=PC,
∴BP=8﹣6=2(cm),
∵点P在线段BC上以2厘米/秒的速度由B点向C点运动,
∴运动时间时1s,
∵△DBP≌△PCQ,
∴BP=CQ=2cm,
∴v=2÷1=2;
当BD=CQ时,△BDP≌△QCP,
∵BD=6cm,PB=PC,
∴QC=6cm,
∵BC=8cm,
∴BP=4cm,
∴运动时间为4÷2=2(s),
∴v=6÷2=3(m/s),
故答案为:2或3.
【分析】此题要分两种情况:①当BD=PC时,△BPD与△CQP全等,计算出BP的长,进而可得运动时间,然后再求v;②当BD=CQ时,△BDP≌△QCP,计算出BP的长,进而可得运动时间,然后再求v.
三、
21、
【答案】解:如图:
【考点】作图—尺规作图的定义,作图—基本作图
【解析】【分析】做出CD的垂直平分线和∠AOB的平分线,其交点P或P′即为所求.
22、
【答案】
(1)解:如图,△A1B1C1即为所求
(2)(1,﹣2);(3,﹣1);(﹣2,1)
(3)解:S△ABC=5×3﹣1\2×3×3﹣1\2×2×1﹣1\2×5×2
=15﹣4.5﹣1﹣5
=4.5
【考点】作图-轴对称变换
【解析】【解答】解:(2)由图可知,A1
(1,﹣2),B1
(3,﹣1),C1
(﹣2,1).
故答案为:(1,﹣2),(3,﹣1),(﹣2,1);
【分析】(1)分别作出各点关于x轴的对称点,再顺次连接即可;(2)根据各点在坐标系中的位置写出各点坐标即可;(3)利用矩形的面积减去三个顶点上三角形的面积即可.
23、
【答案】
(1)证明:∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
∵
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD
(2)证明:∵Rt△ABC≌Rt△BAD,
∴∠CAB=∠DBA,
∴OA=OB,
∴△OAB是等腰三角形
【考点】全等三角形的判定与性质,等腰三角形的判定
【解析】【分析】(1)根据AC⊥BC,BD⊥AD,得出△ABC与△BAD是直角三角形,再根据AC=BD,AB=BA,得出Rt△ABC≌Rt△BAD,即可证出BC=AD,(2)根据Rt△ABC≌Rt△BAD,得出∠CAB=∠DBA,从而证出OA=OB,△OAB是等腰三角形.
24、
【答案】证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF
∴BE+EC=CF+EC
即BC=EF
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS)
【考点】全等三角形的判定
【解析】【分析】根据BE=CF得到BC=EF,然后利用SAS判定定理证明△ABC≌△DEF即可.
25、
【答案】
(1)50°
(2)解:猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
如图:
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
【考点】线段垂直平分线的性质,等腰三角形的性质,轴对称-最短路线问题
【解析】【解答】解:(1)若∠B=70°,则∠NMA的度数是
50°,
故答案为:50°;
【分析】(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;(2)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;(3)根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
同课章节目录
