大熊猫
图片预览




文档简介
苏教版初中数学八年级下册期末考试试题
(考试时间:120分钟,满分150分) 得分
一、选择题(下列各题只有一个答案是正确的,请将正确答案的代号写在题前面的方格中,每题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案
1.已知下列各式中,错误的是…………( )
A. B. C. D.
2.下列分式的运算中,正确的是( )
A、+= B、=
C、 D、
3.反比例函数y=的图象,在每个象限内,y的值随x值的增大而增大,则k的值可为 ( )
A.0 B.1 C.2 D.3
4.下列命题是假命题的是 ( )
A.等角的补角相等 B.内错角相等
C.两点之间,线段最短 D.两点确定一条直线
5.下列说法中正确的是:
A.位似图形一定是相似图形
B.相似图形一定是位似图形
C.两个位似图形一定在位似中心的同侧
D.位似图形中每对对应点所在的直线必互相平行
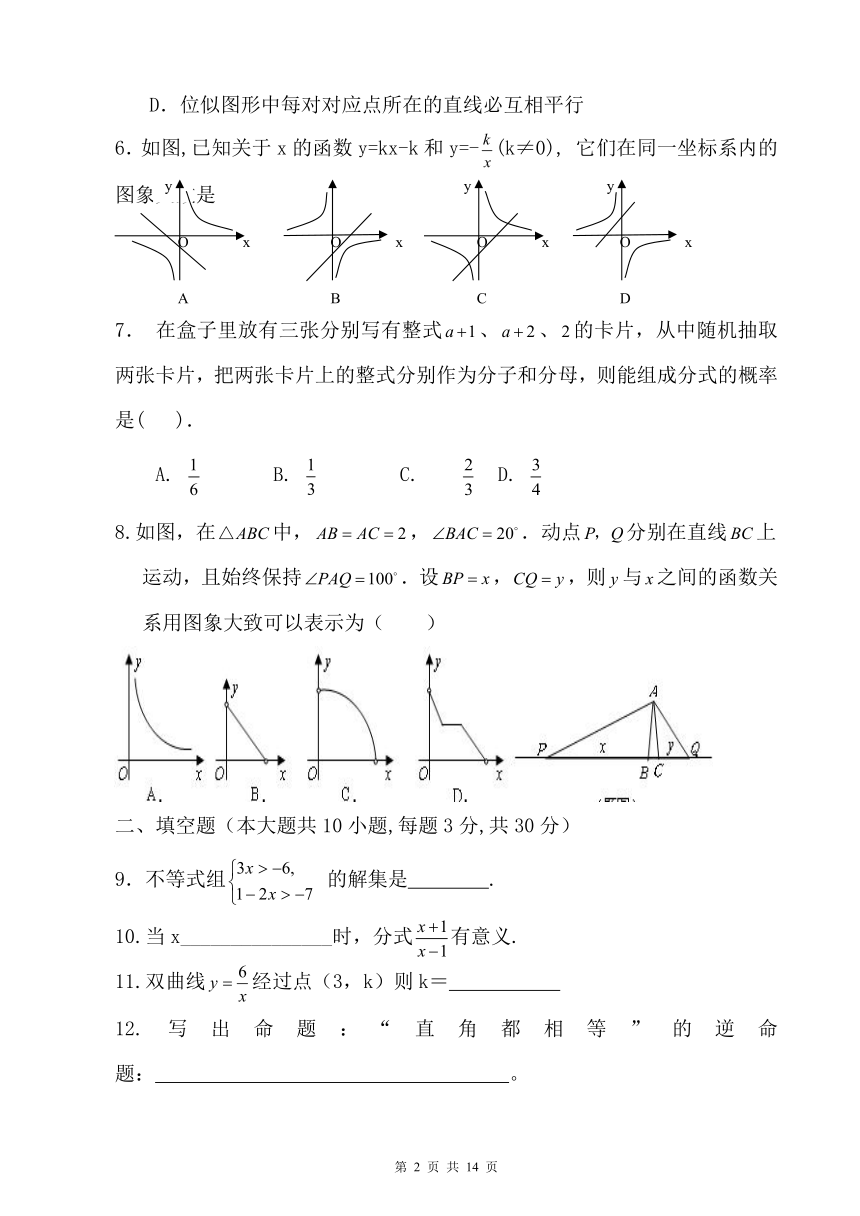
6.如图,已知关于x的函数y=kx-k和y=-(k≠0), 它们在同一坐标系内的图象大致是
7. 在盒子里放有三张分别写有整式、、的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是( ).
A. B. C. D.
8.如图,在中,,.动点分别在直线上运动,且始终保持.设,,则与之间的函数关系用图象大致可以表示为( )
二、填空题(本大题共10小题,每题3分,共30分)
9.不等式组 的解集是 .
10.当x_______________时,分式有意义.
11.双曲线经过点(3,k)则k=
12.写出命题:“直角都相等”的逆命题: 。
13.若反比例函数的图象位于一、三象限内,正比例函数经过二、四象限,则的整数值是 .
14.已知点是线段的黄金分割点,AP>PB,若ABcm,则BP的长度约是 cm(精确到0.1cm)
15.某次电视娱乐节目的现场观众分成红、黄、蓝三个队,其中红队有28人,黄队有30人,蓝队有32人.从这按个队中随机选取一人作为幸运者,这位幸运者恰好是黄队观众的概率为 .
16.如图5,已知Rt△ABC中,∠C=,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE= cm。
17. 数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为米,落在地面上的影长为米,则树高为 __________米.
18.两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;③PA与PB始终相等;
④当点A是PC的中点时,点B一定是PD的中点.
其中一定正确的是 .
三、解答题:(本大题有10题,共96分)
19. (本题满分8分)解不等式组:,并利用数轴求出不等式组的解集。
20. (本题满分8分)先将下式化简,再取一个你喜爱的数代入求值:
21. (本题满分8分)解方程:
+ =
22.(本题满分8分)学生在讨论命题:“如图,梯形中,,,则.”的证明方法时,提出了如下三种思路.
思路1:过一个顶点作另一腰的平行线,转化为等腰三角形和平行四边形;
思路2:过同一底边上的顶点作另一条底边的垂线,转化为直角三角形和矩形;
思路3:延长两腰相交于一点,转化为等腰三角形.
请你结合以上思路,选用一种方法证明该命题.
23.(本题满分10分)
在暴雨到来之前,武警某部承担了一段长150米的河堤加固任务,加固40米后,接到上级抗旱防汛指挥部的指示,要求加快施工进度,为此,该部队在保证施工质量的前提下,投入更多的兵力,每天多加固15米,这样一共用了3天完成了任务。问接到指示后,该部队每天加固河堤多少米?
24.(本题满分10分)如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图像.
①根据图像可知此水池的蓄水量为 m3.
②此函数的解析式为 .
③若要3h排完水,那么每小时的排水量应该是多少
④如果每小时排水量是6m3,那么需要多少小时排完
25. (本题满分10分)有两个可以自由转动的均匀转盘,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).
(1)用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
(2)小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
26. (本题满分10分)如图:BC=30,高AD=20,△ABC的
内接矩形EFGH中,EH : EF = 2:1,
求矩形EFGH的面积。
27. (本题满分12分)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE。过B点折纸片使D点叠在直线AD上,得折痕PQ。
(1)求证:△PBE∽△QAB;
(2)你认为△PBE和△BAE相似吗?如果相似给出证明,如不相似请说明理由;
(3)如果沿直线EB折叠纸片,点A是否能叠在直线EC上?为什么?
28. (本题满12分)
如图,直线y=kx+2与x轴、y轴分别交于点A,B,点C(-1,a)是直线与双曲线
的一个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.
(1)求双曲线及一次函数的解析式;
(2)若在y轴上有一点E,使得以E,A,B为顶点的三角形与△BCD相似,求点E的坐标.
八年级数学试题答案:
1. D 2. C 3. A 4. B 5. A 6. B 7. c 8. A
9. 10. x1 11. 2
12. 相等的角都是直角。13. 4 14. 7.6 15.
16. 1.875 17. 4.2 18. ① ② ④
19. -3≤x<2 …………………………………………4分
( 图略)…………………………………………8分
20. 原式= …………………………………………5分
求值时,x不能取±1 …………………………………………8分
21. 解:x=1………………………………………… 6分
经检验:x=1是增根,所以原方程无解……… 8分
22.过点作交于点,
, 2分
又,
. 4分
,
四边形为平行四边形, 6分
,
.(答案不唯一) 8分
23解:设接到指示后,该部队每天加固河堤X米,则接到指示前每天加固(X-15)米········1分
根据题意,得。················5分
解得,X1 =55,X2=10. ·························8分
经检验,X1 =55,X2=10都是原方程的根,但当X=10时X-15=10-15<0,
∴X=10不合题意,只取X=55。
答:接到指示后,该部队每天加固河堤55米。········10分
24. ① 27 ·························2分
② V= ·························2分
③ 9 m3 ·························3分
④ 4.5小时·························3分
25.⑴ P(3的倍数)= P(5的倍数)=………………5分
⑵ 不公平………………………………………………….7分
得分应修改为:当数字积为3的倍数时得3分;当数字积为5的倍数时得5。
…………………………………………10分
26.解:设EF=x, 则EH=2x…………………………………………..2分
由题意得:………………………………………. 6分
解之得 x= ………………………………………………… 8分
所以,矩形EFGH的面积为………………………………10分
27. 解:(1) 略……………………………………………….4分
(2) 由△PBE∽△QAB 得=,
而PB=QB, 所以=,
又∠EPB=∠EBA=90
所以 △PBE和△BAE相似。………………………………8分
(3)点A能叠在直线EC上。由△PBE和△BAE相似可得∠AEB=∠BEP,
延长AB角EC所在的直线于F,可证BF=AB
所以,点A能叠在直线EC上。……………………………………12分
28.解:(1)双曲线的解析式为 ……………………………………3分
双曲线及一次函数的解析式为 y = -2x + 2…………………………3分
(2) ①点E与原点O重合,E(0,0) …………………………3分
② 当△BEA∽△BCD时,E(0,-) …………………………3分
附件2:
泰州市2009年中小学教师命题竞赛评选申报表
姓 名 朱桂平 所在学校 九龙实验学校 学 科 数学
教材版本 苏科版 职 称 中教一级 联系电话 15952955830
Emal jlsxzgp@
命制试卷名称 八下期末试卷 参考答案(有无) 有 评分标准(有无) 有
命题意图(有无) 有 创新题所占比例 35℅ 电子文稿(是否上传) 是
附件3:
泰州市2009年中小学教师命题竞赛双向细目表
题号 考查内容(知识、技能、思维能力等) 试题来源 难度预测(得分率) 备注
1 解不等式 改编 0.95
2 分式的化简 原创 0.9
3 反比例函数的性质 改编 0.9
4 假命题概念考查 原创 0.9
5 位似图形的性质 原创 0.8
6 一次函数、反比例函数的图象 改编 0.5
7 简单的概率 原创 0.9
8 相似与反比例的图像 原创 0.2
9 解不等式组 改编 0.9
10 分式的意义 改编 0.9
11 双曲线的解析式 改编 0.9
12 关于逆命题 原创 0.9
13 函数与不等式 改编 0.8
14 关于黄金分割 改编 0.9
15 简单的概率 原创 0.9
16 运用相似求值 改编 0.6
17 运用比例求值 改编 0.5
18 反比例函数的图像 改编 0.3
19 解不等式组 改编 0.9
20 分式的化简求值 原创 0.9
21 解分式方程 改编 0.9
22 简单的几何证明 原创 0.9
23 分式方程的应用 改编 0.8
24 反比例函数的应用 原创 0.8
25 关于游戏公平(概率) 改编 0.7
26 相似三角形的应用 原创 0.6
27 相似三角形的证明 改编 0.5
28 反比例与相似的结合 改编 0.3
命题说明
1、立足课本。试题以严格按照《数学课程标准》的“数与代数”,
“空间与图形”, “概率与统计”,“实践与综合运用(课题学习)”这四个学习领域和实行的教材中共有部分的内容进行组织和命题,既注意到知识的覆盖面,更重视了数学知识的内在联系。关注课本以及与课本配套的练习册。试卷28个题目中,有16个题目,是依据课本、练习册的习题改编。
2、适当关注了2008年中考试题中,与八年级下学期学习内容相关的部分。
3.试题着重考查八年级数学的基础知识、基本技能、基本的数学思想方法,以及数感、符号感、空间观念、统计观念、应用意识和推理能力等数学思考和解决问题的能力。同时,结合具体情境考查对学生情感与态度方面培养的效果,感受证明的必要性、证明过程的严谨性和数学结论的确定性,以及实事求是的态度和对问题进行质疑和独立思考的习惯等。
4.试卷题型编排按选择题、填空题、解答题三种题型依次排列,试卷非常重视降低起点、减缓坡度、控制难度。命题设计的难度比例为7:2:1
学校------------------------班级----------------姓名---------------考试号---------------
----------------------------------------------------装-----------------------------订-------------------------线--------------------------------
Q
B
C
D
A
M
N
B
C
D
(
A
B
5
6
4
A
3
2
1
9
3
O
t
V
(第24题图)
B
C
D
A
B
A
F
C
D
G
D
x
O
E
y
B
x
O
C
x
P
y
N
O
A
x
y
O
E
C
A
B
D
E
y
x
M
H
PAGE
第 1 页 共 14 页
(考试时间:120分钟,满分150分) 得分
一、选择题(下列各题只有一个答案是正确的,请将正确答案的代号写在题前面的方格中,每题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案
1.已知下列各式中,错误的是…………( )
A. B. C. D.
2.下列分式的运算中,正确的是( )
A、+= B、=
C、 D、
3.反比例函数y=的图象,在每个象限内,y的值随x值的增大而增大,则k的值可为 ( )
A.0 B.1 C.2 D.3
4.下列命题是假命题的是 ( )
A.等角的补角相等 B.内错角相等
C.两点之间,线段最短 D.两点确定一条直线
5.下列说法中正确的是:
A.位似图形一定是相似图形
B.相似图形一定是位似图形
C.两个位似图形一定在位似中心的同侧
D.位似图形中每对对应点所在的直线必互相平行
6.如图,已知关于x的函数y=kx-k和y=-(k≠0), 它们在同一坐标系内的图象大致是
7. 在盒子里放有三张分别写有整式、、的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是( ).
A. B. C. D.
8.如图,在中,,.动点分别在直线上运动,且始终保持.设,,则与之间的函数关系用图象大致可以表示为( )
二、填空题(本大题共10小题,每题3分,共30分)
9.不等式组 的解集是 .
10.当x_______________时,分式有意义.
11.双曲线经过点(3,k)则k=
12.写出命题:“直角都相等”的逆命题: 。
13.若反比例函数的图象位于一、三象限内,正比例函数经过二、四象限,则的整数值是 .
14.已知点是线段的黄金分割点,AP>PB,若ABcm,则BP的长度约是 cm(精确到0.1cm)
15.某次电视娱乐节目的现场观众分成红、黄、蓝三个队,其中红队有28人,黄队有30人,蓝队有32人.从这按个队中随机选取一人作为幸运者,这位幸运者恰好是黄队观众的概率为 .
16.如图5,已知Rt△ABC中,∠C=,AC=4cm,BC=3cm,现将△ABC进行折叠,使顶点A、B重合,则折痕DE= cm。
17. 数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为米,落在地面上的影长为米,则树高为 __________米.
18.两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;③PA与PB始终相等;
④当点A是PC的中点时,点B一定是PD的中点.
其中一定正确的是 .
三、解答题:(本大题有10题,共96分)
19. (本题满分8分)解不等式组:,并利用数轴求出不等式组的解集。
20. (本题满分8分)先将下式化简,再取一个你喜爱的数代入求值:
21. (本题满分8分)解方程:
+ =
22.(本题满分8分)学生在讨论命题:“如图,梯形中,,,则.”的证明方法时,提出了如下三种思路.
思路1:过一个顶点作另一腰的平行线,转化为等腰三角形和平行四边形;
思路2:过同一底边上的顶点作另一条底边的垂线,转化为直角三角形和矩形;
思路3:延长两腰相交于一点,转化为等腰三角形.
请你结合以上思路,选用一种方法证明该命题.
23.(本题满分10分)
在暴雨到来之前,武警某部承担了一段长150米的河堤加固任务,加固40米后,接到上级抗旱防汛指挥部的指示,要求加快施工进度,为此,该部队在保证施工质量的前提下,投入更多的兵力,每天多加固15米,这样一共用了3天完成了任务。问接到指示后,该部队每天加固河堤多少米?
24.(本题满分10分)如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图像.
①根据图像可知此水池的蓄水量为 m3.
②此函数的解析式为 .
③若要3h排完水,那么每小时的排水量应该是多少
④如果每小时排水量是6m3,那么需要多少小时排完
25. (本题满分10分)有两个可以自由转动的均匀转盘,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).
(1)用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
(2)小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
26. (本题满分10分)如图:BC=30,高AD=20,△ABC的
内接矩形EFGH中,EH : EF = 2:1,
求矩形EFGH的面积。
27. (本题满分12分)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE。过B点折纸片使D点叠在直线AD上,得折痕PQ。
(1)求证:△PBE∽△QAB;
(2)你认为△PBE和△BAE相似吗?如果相似给出证明,如不相似请说明理由;
(3)如果沿直线EB折叠纸片,点A是否能叠在直线EC上?为什么?
28. (本题满12分)
如图,直线y=kx+2与x轴、y轴分别交于点A,B,点C(-1,a)是直线与双曲线
的一个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.
(1)求双曲线及一次函数的解析式;
(2)若在y轴上有一点E,使得以E,A,B为顶点的三角形与△BCD相似,求点E的坐标.
八年级数学试题答案:
1. D 2. C 3. A 4. B 5. A 6. B 7. c 8. A
9. 10. x1 11. 2
12. 相等的角都是直角。13. 4 14. 7.6 15.
16. 1.875 17. 4.2 18. ① ② ④
19. -3≤x<2 …………………………………………4分
( 图略)…………………………………………8分
20. 原式= …………………………………………5分
求值时,x不能取±1 …………………………………………8分
21. 解:x=1………………………………………… 6分
经检验:x=1是增根,所以原方程无解……… 8分
22.过点作交于点,
, 2分
又,
. 4分
,
四边形为平行四边形, 6分
,
.(答案不唯一) 8分
23解:设接到指示后,该部队每天加固河堤X米,则接到指示前每天加固(X-15)米········1分
根据题意,得。················5分
解得,X1 =55,X2=10. ·························8分
经检验,X1 =55,X2=10都是原方程的根,但当X=10时X-15=10-15<0,
∴X=10不合题意,只取X=55。
答:接到指示后,该部队每天加固河堤55米。········10分
24. ① 27 ·························2分
② V= ·························2分
③ 9 m3 ·························3分
④ 4.5小时·························3分
25.⑴ P(3的倍数)= P(5的倍数)=………………5分
⑵ 不公平………………………………………………….7分
得分应修改为:当数字积为3的倍数时得3分;当数字积为5的倍数时得5。
…………………………………………10分
26.解:设EF=x, 则EH=2x…………………………………………..2分
由题意得:………………………………………. 6分
解之得 x= ………………………………………………… 8分
所以,矩形EFGH的面积为………………………………10分
27. 解:(1) 略……………………………………………….4分
(2) 由△PBE∽△QAB 得=,
而PB=QB, 所以=,
又∠EPB=∠EBA=90
所以 △PBE和△BAE相似。………………………………8分
(3)点A能叠在直线EC上。由△PBE和△BAE相似可得∠AEB=∠BEP,
延长AB角EC所在的直线于F,可证BF=AB
所以,点A能叠在直线EC上。……………………………………12分
28.解:(1)双曲线的解析式为 ……………………………………3分
双曲线及一次函数的解析式为 y = -2x + 2…………………………3分
(2) ①点E与原点O重合,E(0,0) …………………………3分
② 当△BEA∽△BCD时,E(0,-) …………………………3分
附件2:
泰州市2009年中小学教师命题竞赛评选申报表
姓 名 朱桂平 所在学校 九龙实验学校 学 科 数学
教材版本 苏科版 职 称 中教一级 联系电话 15952955830
Emal jlsxzgp@
命制试卷名称 八下期末试卷 参考答案(有无) 有 评分标准(有无) 有
命题意图(有无) 有 创新题所占比例 35℅ 电子文稿(是否上传) 是
附件3:
泰州市2009年中小学教师命题竞赛双向细目表
题号 考查内容(知识、技能、思维能力等) 试题来源 难度预测(得分率) 备注
1 解不等式 改编 0.95
2 分式的化简 原创 0.9
3 反比例函数的性质 改编 0.9
4 假命题概念考查 原创 0.9
5 位似图形的性质 原创 0.8
6 一次函数、反比例函数的图象 改编 0.5
7 简单的概率 原创 0.9
8 相似与反比例的图像 原创 0.2
9 解不等式组 改编 0.9
10 分式的意义 改编 0.9
11 双曲线的解析式 改编 0.9
12 关于逆命题 原创 0.9
13 函数与不等式 改编 0.8
14 关于黄金分割 改编 0.9
15 简单的概率 原创 0.9
16 运用相似求值 改编 0.6
17 运用比例求值 改编 0.5
18 反比例函数的图像 改编 0.3
19 解不等式组 改编 0.9
20 分式的化简求值 原创 0.9
21 解分式方程 改编 0.9
22 简单的几何证明 原创 0.9
23 分式方程的应用 改编 0.8
24 反比例函数的应用 原创 0.8
25 关于游戏公平(概率) 改编 0.7
26 相似三角形的应用 原创 0.6
27 相似三角形的证明 改编 0.5
28 反比例与相似的结合 改编 0.3
命题说明
1、立足课本。试题以严格按照《数学课程标准》的“数与代数”,
“空间与图形”, “概率与统计”,“实践与综合运用(课题学习)”这四个学习领域和实行的教材中共有部分的内容进行组织和命题,既注意到知识的覆盖面,更重视了数学知识的内在联系。关注课本以及与课本配套的练习册。试卷28个题目中,有16个题目,是依据课本、练习册的习题改编。
2、适当关注了2008年中考试题中,与八年级下学期学习内容相关的部分。
3.试题着重考查八年级数学的基础知识、基本技能、基本的数学思想方法,以及数感、符号感、空间观念、统计观念、应用意识和推理能力等数学思考和解决问题的能力。同时,结合具体情境考查对学生情感与态度方面培养的效果,感受证明的必要性、证明过程的严谨性和数学结论的确定性,以及实事求是的态度和对问题进行质疑和独立思考的习惯等。
4.试卷题型编排按选择题、填空题、解答题三种题型依次排列,试卷非常重视降低起点、减缓坡度、控制难度。命题设计的难度比例为7:2:1
学校------------------------班级----------------姓名---------------考试号---------------
----------------------------------------------------装-----------------------------订-------------------------线--------------------------------
Q
B
C
D
A
M
N
B
C
D
(
A
B
5
6
4
A
3
2
1
9
3
O
t
V
(第24题图)
B
C
D
A
B
A
F
C
D
G
D
x
O
E
y
B
x
O
C
x
P
y
N
O
A
x
y
O
E
C
A
B
D
E
y
x
M
H
PAGE
第 1 页 共 14 页
