青岛版八年级上册课件 第二章 2.5 角平分线的性质(共29张PPT)
文档属性
| 名称 | 青岛版八年级上册课件 第二章 2.5 角平分线的性质(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-13 00:00:00 | ||
图片预览







文档简介
课件29张PPT。2.5 角平分线的性质温故知新1、如图,哪条线段是点P到直线MN的距离( )A、线段PA
B、线段PB
C、线段PC
D、线段PDC温故知新2、如图,哪条线段是点P到直线MN的距离最短的线段( )A、线段PA
B、线段PB
C、线段PC
D、线段PDC理由:垂线段最短。温故知新3、如图,哪条线段是两条平行线之间的距离( )A、线段PA
B、线段PB
C、线段PC
D、线段PDC温故知新3、如图,哪条线段是两条平行线之间的距离( )A、线段PA
B、线段PB
C、线段PC
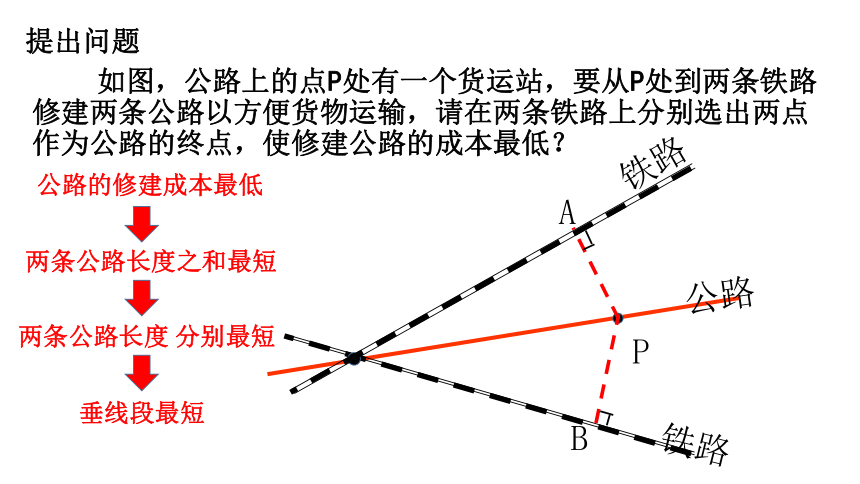
D、线段PDC提出问题
如图,公路上的点P处有一个货运站,要从P处到两条铁路修建两条公路以方便货物运输,请在两条铁路上分别选出两点作为公路的终点,使修建公路的成本最低?P铁路公路铁路公路的修建成本最低两条公路长度之和最短两条公路长度 分别最短垂线段最短AB1.能探索出并准确叙述出角的轴对称性。
2.能探索出角平分线性质和判定。
3.会用尺规作一个角的平分线。
4.能灵活运用角平分线的性质与判定解决有关问题。
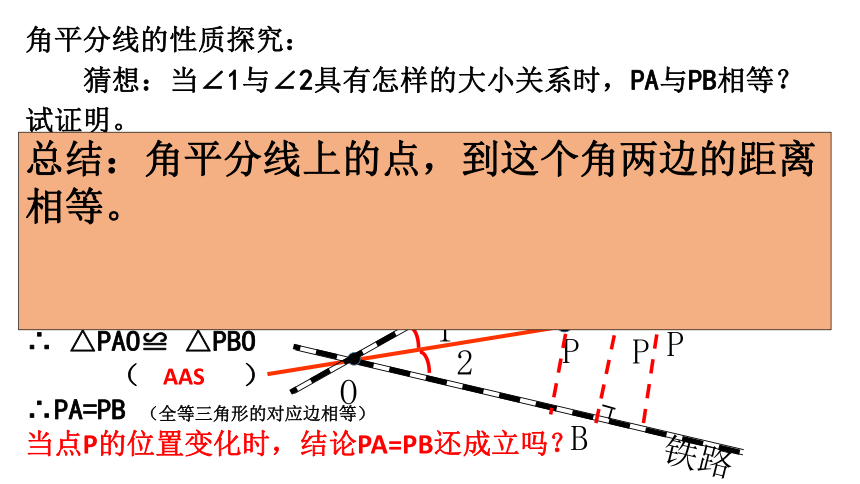
学习目标考点(重点)(重点)(关键)(重点)P铁路公路铁路AB角平分线的性质探究:
猜想:当∠1与∠2具有怎样的大小关系时,PA与PB相等?
试证明。O猜想:∠1 ∠2证明:在△PAO与△PBO中:
∠ =∠ (直角)
∠ =∠ (已知)
= (公共边)
∴ △PAO≌ △PBO
( )
∴PA=PB (全等三角形的对应边相等)
当点P的位置变化时,结论PA=PB还成立吗?PAO PBO 1 2 PO PO AASPP=总结:角平分线上的点,到这个角两边的距离相等。
角平分线上的点,到这个角的两边的距离相等.
符号表达:BACP12角平分线的性质温馨提示:
该性质主要用于判断或证明两线段相等,
不必再证全等∵AD平分∠BAC PM⊥AB PN⊥AC∴PM=PND判断正误,并说明理由:
(1)如图1,P在射线OC上,PE⊥OA,PF⊥OB,则PE=PF.( )
(2)如图2,P是∠AOB的平分线OC上的一点,E、F分别在OA、OB上,则PE=PF. ( )图1(3)如图3,在∠AOB的平分线OC上任取一点P, 若P到OA的距离为3cm,则P到OB的距离边为3cm.( )辨一辨∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC,∴PD=PE.同理可证:PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等.证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,例1.如图,△ABC的角平分线 BM、CN相交于点P。 求证:点P到三边AB、BC、CA的距离相等PMN点P在∠A的平分线上吗
典例示范P铁路公路铁路AB问题变式:(角平分线的判定)
已知:PA=PB,OA=OB;
猜想:①两个三角形有怎样的关系?②比较角1和角2的大小?③公路和两条铁路有怎样的
位置关系?O④点P的位置变化时,
已知条件不变,
∠1=∠2还成立吗? 由此得出什么结论?总结:角的内部到角两边的距离相等的点在角的平分线上。
角的内部到角的两边距离相等的
点在角的平分线上.符号语言:∵ PM⊥AB PN⊥AC PM=PN
∴AP平分∠BAC角平分线的判定温馨提示:
该判定主要用于证明两角相等,角的平分线的性质OP平分∠AOBPD⊥OA于DPE⊥OB于EPD=PEOP平分∠AOBPD=PEPD⊥OA于DPE⊥OB于E角的平分线的判定归纳、比较性质用于证明两线段相等 判定用于证明两角相等∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC,∴PD=PE.同理可证:PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等.证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,如图,△ABC的角平分线 BM、CN相交于点P。 求证:点P到三边AB、BC、CA的距离相等PMN典例示范点P在∠A的平分线上吗
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.角平分线的画法你会作角的平分线吗? 怎样作一个角的平分线?(不用量角器)观察领悟作法,探索思考证明方法CA思考:已知:∠BAC
求作:∠BAC的平分线APBF作法: 1、以A为圆心,适当长
为半径作弧,交AB于E,
交AC于F.2、分别以E、F为圆心,
大于 的长为半径作弧,
两弧在∠BAC内部交于点P.3、作射线AP,射线AP即为所求.则射线AP即为所求。尺规作角的平分线你能证明射线AP,就是∠BAC的角平分线吗?求证: AP是∠BAC的角平分线证明:连结PE,PF,尺规作角的平分线A情境再现 三条公路的交叉处是一个三角形区域,现在要在此区域内建一个加油站,使得该加油站到三条路的距离相等。试问加油站应建在什么位置,你能帮助设计者确定此加油站的位置吗?【学以致用】则点A即为所求。 如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个加油站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置. 拓展延伸P1P2P3P4l1l2l31.∠AOB的平分线上一点P到OA的距离为5,
Q是OB上任一点,则( )
A. PQ>5 B. PQ≥5 C. PQ﹤5 D. PQ≤5B拓展提升 走近中考2.△ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC
于F,AB=10厘米,AC=8厘米,△ABC的面积为45平
方厘米,则DE的长______.
5cm3.如图,在直角坐标系中,AD是∠OAB的角平分线,点D的坐标是(2,0),点D到AB的距离为____。E4.在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?利用直尺和圆规作出这个点。
P则点P即为所求。 1.角平分线的性质:角是轴对称图形
在角平分线上的点到角的两边的距离相等
2.角平分线的判定:
角的内部到一个角的两边的距离相等的点,在这个角平分线上。
4.角平分线的性质是线段相等的新途径.
角平分线的判定是证明角相等(或证明点在直线上)的根据之一.3.性质和判定的关系
点在角平分线上 点到角两边的距离相等 总结归纳5.用尺规作一个角的平分线.二、思想方法:
观察、猜想、类比、转化、逆向思维都是常用的数学思想方法。
一、知识收获:
1.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则 M到OB的距离为 ㎝。3. 如图,OP 平分∠MON,PA⊥ON,
垂足为 A,PA = 2. Q是边 OM 上的
一个动点,则线段 PQ的最小值( )
A.1 B.2 C.3 D.42. 如图,在△ABC中,∠C=90°,
DE⊥AB,∠1=∠2,且
AC=6cm,那么线段BE是∠ABC
的 ,AE+DE= 。1.5角平分线6cmB达标测试5.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上. GHM4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足 分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE
C、∠DPO=∠EPO D、PD=ODD5.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上. 证明:过点F作FG⊥AE于G,FH⊥AD
于H,FM⊥BC于M.GHM∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC,∴FG=FM.又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,∴FM=FH.∴FG=FH.∴点F在∠DAE的平分线上. 达标要求:
4号 全对即为达标,
3号最多错1个即为达标,
2号最多错2个即为达标,
1号最多错3个即为达标。
做完后同桌互批,组长做好分数统计。达标测评
B、线段PB
C、线段PC
D、线段PDC温故知新2、如图,哪条线段是点P到直线MN的距离最短的线段( )A、线段PA
B、线段PB
C、线段PC
D、线段PDC理由:垂线段最短。温故知新3、如图,哪条线段是两条平行线之间的距离( )A、线段PA
B、线段PB
C、线段PC
D、线段PDC温故知新3、如图,哪条线段是两条平行线之间的距离( )A、线段PA
B、线段PB
C、线段PC
D、线段PDC提出问题
如图,公路上的点P处有一个货运站,要从P处到两条铁路修建两条公路以方便货物运输,请在两条铁路上分别选出两点作为公路的终点,使修建公路的成本最低?P铁路公路铁路公路的修建成本最低两条公路长度之和最短两条公路长度 分别最短垂线段最短AB1.能探索出并准确叙述出角的轴对称性。
2.能探索出角平分线性质和判定。
3.会用尺规作一个角的平分线。
4.能灵活运用角平分线的性质与判定解决有关问题。
学习目标考点(重点)(重点)(关键)(重点)P铁路公路铁路AB角平分线的性质探究:
猜想:当∠1与∠2具有怎样的大小关系时,PA与PB相等?
试证明。O猜想:∠1 ∠2证明:在△PAO与△PBO中:
∠ =∠ (直角)
∠ =∠ (已知)
= (公共边)
∴ △PAO≌ △PBO
( )
∴PA=PB (全等三角形的对应边相等)
当点P的位置变化时,结论PA=PB还成立吗?PAO PBO 1 2 PO PO AASPP=总结:角平分线上的点,到这个角两边的距离相等。
角平分线上的点,到这个角的两边的距离相等.
符号表达:BACP12角平分线的性质温馨提示:
该性质主要用于判断或证明两线段相等,
不必再证全等∵AD平分∠BAC PM⊥AB PN⊥AC∴PM=PND判断正误,并说明理由:
(1)如图1,P在射线OC上,PE⊥OA,PF⊥OB,则PE=PF.( )
(2)如图2,P是∠AOB的平分线OC上的一点,E、F分别在OA、OB上,则PE=PF. ( )图1(3)如图3,在∠AOB的平分线OC上任取一点P, 若P到OA的距离为3cm,则P到OB的距离边为3cm.( )辨一辨∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC,∴PD=PE.同理可证:PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等.证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,例1.如图,△ABC的角平分线 BM、CN相交于点P。 求证:点P到三边AB、BC、CA的距离相等PMN点P在∠A的平分线上吗
典例示范P铁路公路铁路AB问题变式:(角平分线的判定)
已知:PA=PB,OA=OB;
猜想:①两个三角形有怎样的关系?②比较角1和角2的大小?③公路和两条铁路有怎样的
位置关系?O④点P的位置变化时,
已知条件不变,
∠1=∠2还成立吗? 由此得出什么结论?总结:角的内部到角两边的距离相等的点在角的平分线上。
角的内部到角的两边距离相等的
点在角的平分线上.符号语言:∵ PM⊥AB PN⊥AC PM=PN
∴AP平分∠BAC角平分线的判定温馨提示:
该判定主要用于证明两角相等,角的平分线的性质OP平分∠AOBPD⊥OA于DPE⊥OB于EPD=PEOP平分∠AOBPD=PEPD⊥OA于DPE⊥OB于E角的平分线的判定归纳、比较性质用于证明两线段相等 判定用于证明两角相等∵BM是△ABC的角平分线,
PD⊥AB,PE⊥BC,∴PD=PE.同理可证:PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等.证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,如图,△ABC的角平分线 BM、CN相交于点P。 求证:点P到三边AB、BC、CA的距离相等PMN典例示范点P在∠A的平分线上吗
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.角平分线的画法你会作角的平分线吗? 怎样作一个角的平分线?(不用量角器)观察领悟作法,探索思考证明方法CA思考:已知:∠BAC
求作:∠BAC的平分线APBF作法: 1、以A为圆心,适当长
为半径作弧,交AB于E,
交AC于F.2、分别以E、F为圆心,
大于 的长为半径作弧,
两弧在∠BAC内部交于点P.3、作射线AP,射线AP即为所求.则射线AP即为所求。尺规作角的平分线你能证明射线AP,就是∠BAC的角平分线吗?求证: AP是∠BAC的角平分线证明:连结PE,PF,尺规作角的平分线A情境再现 三条公路的交叉处是一个三角形区域,现在要在此区域内建一个加油站,使得该加油站到三条路的距离相等。试问加油站应建在什么位置,你能帮助设计者确定此加油站的位置吗?【学以致用】则点A即为所求。 如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个加油站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置. 拓展延伸P1P2P3P4l1l2l31.∠AOB的平分线上一点P到OA的距离为5,
Q是OB上任一点,则( )
A. PQ>5 B. PQ≥5 C. PQ﹤5 D. PQ≤5B拓展提升 走近中考2.△ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC
于F,AB=10厘米,AC=8厘米,△ABC的面积为45平
方厘米,则DE的长______.
5cm3.如图,在直角坐标系中,AD是∠OAB的角平分线,点D的坐标是(2,0),点D到AB的距离为____。E4.在V型公路(∠AOB)内部,有两个村庄C、D。你能选择一个纺织厂的厂址P,使P到V型公路的距离相等,且使C、D两村的工人上下班的路程一样吗?利用直尺和圆规作出这个点。
P则点P即为所求。 1.角平分线的性质:角是轴对称图形
在角平分线上的点到角的两边的距离相等
2.角平分线的判定:
角的内部到一个角的两边的距离相等的点,在这个角平分线上。
4.角平分线的性质是线段相等的新途径.
角平分线的判定是证明角相等(或证明点在直线上)的根据之一.3.性质和判定的关系
点在角平分线上 点到角两边的距离相等 总结归纳5.用尺规作一个角的平分线.二、思想方法:
观察、猜想、类比、转化、逆向思维都是常用的数学思想方法。
一、知识收获:
1.∠AOB的平分线上一点M,M到OA的距离为1.5㎝,则 M到OB的距离为 ㎝。3. 如图,OP 平分∠MON,PA⊥ON,
垂足为 A,PA = 2. Q是边 OM 上的
一个动点,则线段 PQ的最小值( )
A.1 B.2 C.3 D.42. 如图,在△ABC中,∠C=90°,
DE⊥AB,∠1=∠2,且
AC=6cm,那么线段BE是∠ABC
的 ,AE+DE= 。1.5角平分线6cmB达标测试5.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上. GHM4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足 分别为D,E,下列结论错误的是( )
A、PD=PE B、OD=OE
C、∠DPO=∠EPO D、PD=ODD5.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上. 证明:过点F作FG⊥AE于G,FH⊥AD
于H,FM⊥BC于M.GHM∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC,∴FG=FM.又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,∴FM=FH.∴FG=FH.∴点F在∠DAE的平分线上. 达标要求:
4号 全对即为达标,
3号最多错1个即为达标,
2号最多错2个即为达标,
1号最多错3个即为达标。
做完后同桌互批,组长做好分数统计。达标测评
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
