第3章 图形的相似单元检测A卷
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
21世纪教育网 –中小学教育资源及组卷应用平台
图形的相似单元检测A卷
姓名:__________班级:__________学号:__________
、选择题(本大题共12小题)
若≠0,则=( )
A. B. C. D.无法确定
如果点C为线段AB的黄金分割点,且AC>BC,则下列各式不正确的是( )
A.AB:AC=AC:BC B.AC= C.AB= D.BC≈0.618AB
如图,已知AB∥CD∥EF,那么下列结论正确的是()
A. B. C. D.
已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )
A.1:4 B.4:1 C.1:2 D.2:1
如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A.6 B.12 C.18 D.24
如图,路灯AB的高度为8米,树CD与路灯的水平距离为4米,则得树在灯光下的影长DE为3米,则树高( )
A.4米 B.6米 C.米 D.米
如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
下列各组图形不一定相似的是( )
A.两个等腰直角三角形, B.各有一个角是100°的两个等腰三角形
C.两个矩形 D.各有一个角是50°的两个直角三角形
如图所示,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF︰FC等于( )
A.3︰2 B.3︰1 C.1︰1 D.1︰2
如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )
A.1.5米 B.2.3米 C.3.2米 D.7.8米
CD是△ABC中AB边上的高,已知CD=6,DA=3,DB=12,则( )
A.CA2+BC2=AB2 B.∠CAB=∠CBD C.∠CAB>∠ACB D.∠ACD=∠BCD
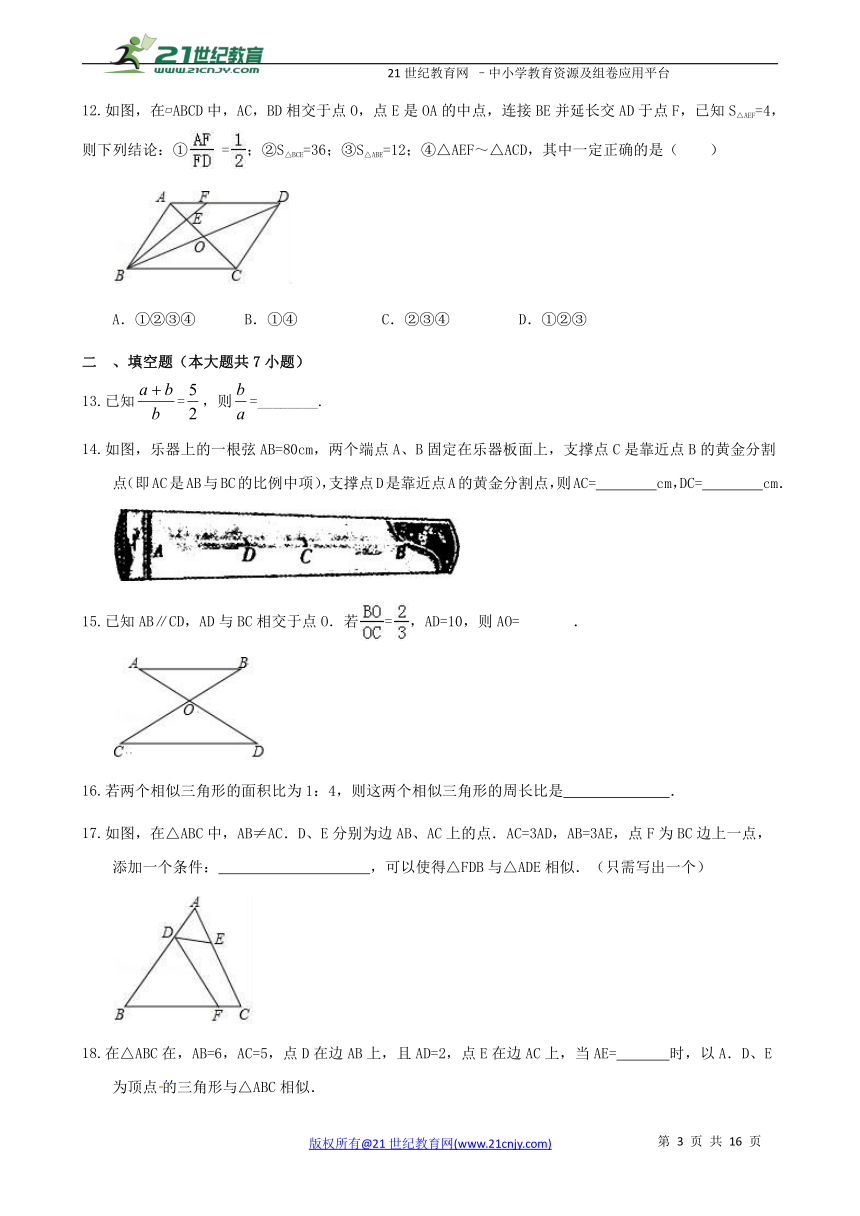
如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① =;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②③
、填空题(本大题共7小题)
已知=,则=________.
如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点(即AC是AB与BC的比例中项),支撑点D是靠近点A的黄金分割点,则AC= cm,DC= cm.
已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO= .
若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是 .
如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: ,可以使得△FDB与△ADE相似.(只需写出一个)
在△ABC在,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE= 时,以A.D、E为顶点的三角形与△ABC相似.
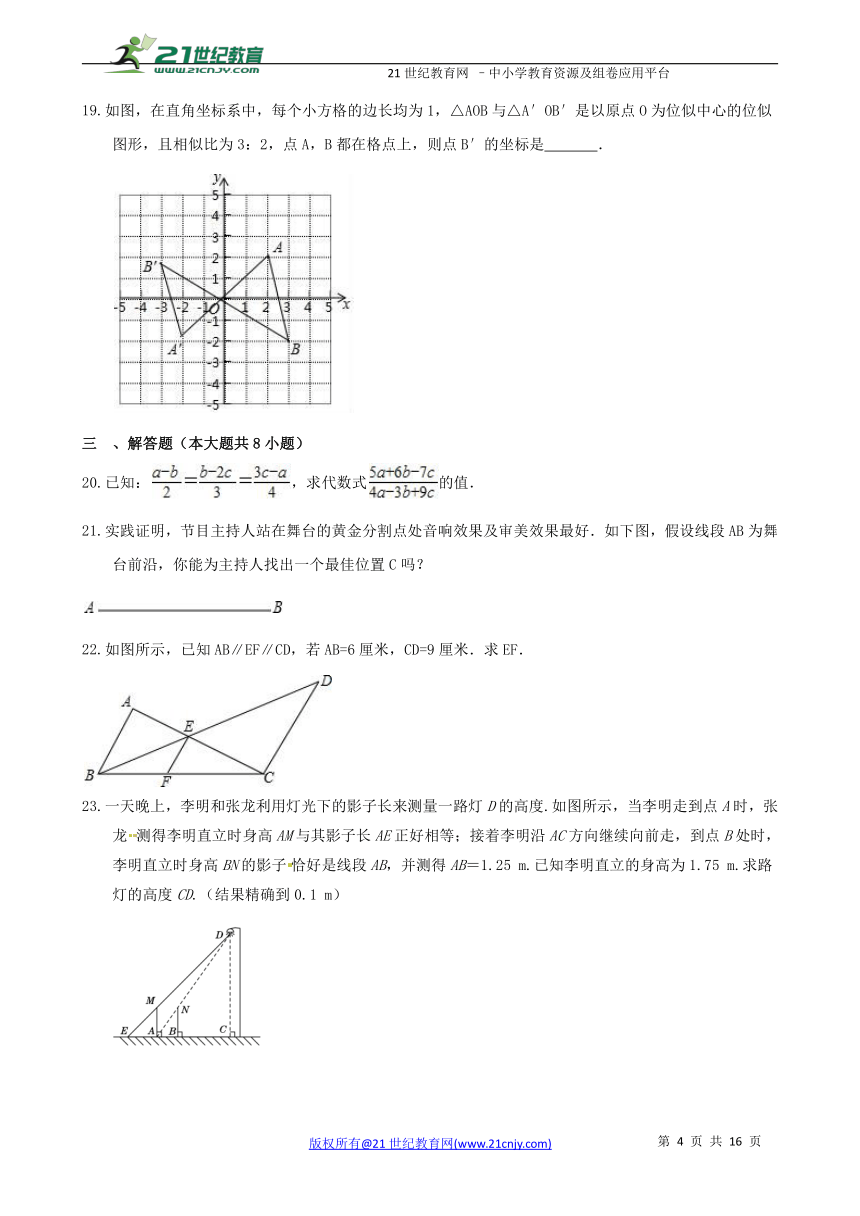
如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是 .
、解答题(本大题共8小题)
已知:,求代数式的值.
实践证明,节目主持人站在舞台的黄金分割点处音响效果及审美效果最好.如下图,假设线段AB为舞台前沿,你能为主持人找出一个最佳位置C吗?
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图所示,当李明走到点A时,张龙测得李明直立时身高AM与其影子长AE正好相等;接着李明沿AC方向继续向前走,到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立的身高为1.75 m.求路灯的高度CD.(结果精确到0.1 m)
已知任意三角形ABC,其面积为S.作BC的平行线与AB、AC分别交于D、E.设三角形BDE的面积为M,求证:M≤.
如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
如图,在9×10的正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;
(2)求△DFB和△DCE的面积比.
以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)求证:AM2=AD DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
答案解析
、选择题
【分析】设比值为k,然后用k表示出a、b、c,再代入算式进行计算即可求解.
解:设=k,
则a=2k,b=3k,c=4k,
∴==.
故选B.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值( )叫做黄金比.
解:∵AC>BC,
∴AC是较长的线段,
根据黄金分割的定义可知:AB:AC=AC:BC,AC=AB,AB=,AC≈0.618AB.
故选D.
【分析】 已知AB∥CD∥EF,根据平行线分线段成比例定理,对各项进行分析即可.
解:∵AB∥CD∥EF,
∴=.
故选D.
【分析】利用相似三角形面积之比等于相似比的平方计算即可.
解:∵△ABC∽△DEF,且相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选A
【分析】根据线段中点的性质求出AD=AB、AE=AC的长,根据三角形中位线定理求出DE=AB,根据三角形周长公式计算即可.
解:∵D、E分别是AB、AC的中点,
∴AD=AB,AE=AC,DE=BC,
∴△ABC的周长=AB+AC+BC=2AD+2AE+2DE=2(AD+AE+DE)=2×6=12.
故选B.
【分析】由于人和地面是垂直的,即和路灯平行,构成相似三角形.根据对应边成比例,列方程解答即可.
解:因为CD∥AB,
∴△AEB∽△CED,
∴AB:CD=BE:ED,
即8:CD=7:3
解得:AB=m.
故选D.
【分析】先求出位似比,根据位似比等于相似比,再由相似三角形的面积比等于相似比的平方即可.
解:由位似变换的性质可知,A′B′∥AB,A′C′∥AC,
∴△A′B′C′∽△ABC.
∵△A'B'C'与△ABC的面积的比4:9,
∴△A'B'C'与△ABC的相似比为2:3,
∴=
故选:A.
【分析】根据相似图形的定义,对应边成比例,对应角相等对各选项分析判断。
解:A.两个等腰直角三角形,对应边成比例,对应角相等,符合定义,一定相似,故正确;
B、各有一个角是100°的两个等腰三角形,100°的角一定是顶角,其余两角一定相等,故一定相似,故正确;
C、两个矩形,四个角都是直角,但四条边不一定对应成比例,不一定相似,故错误;
D、各有一个角是50°的两个直角三角形,都有一个直角,根据两角对应相等,两三角形相似,故正确。
故选C
【分析】根据平行四边形的性质和相似三角形的判定与性质求解
解: ∵ ABCD,故AD∥BC,
∴△DEF∽△BCF,
∴DE:BC=EF:FC,
∵点E是边AD的中点,
∴AE=DE=AD,
∴EF:FC=1:2.
故选D.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
解: 设树高为x米,
因为,
所以
解得:x=3.2.
故选C.
【分析】画出图形,根据CD、DA计算AC,根据DB、DA计算AB,解直角△ACD、直角△CBD则可得A选项正确.
解:CA2+BC2=AD2+CD2+BD2+CD2=144+36+36+9=225,
AB=DA+DB=15,AB2=225,
∴CA2+BC2=AB2=225,(A选项正确)
且AD=3,CD=6,BD=12,CD⊥AB,
∴△BCD∽△CAD,
∠ACD=∠CBD,∠BCD=∠CAD,(故B、D选项错误),
在△ABC中,AB>BC,
∠CAB<∠ACB,(故C选项错误).
故选A.
【分析】根据平行四边形的性质得到AE=CE,根据相似三角形的性质得到==,等量代换得到AF=AD,于是得到=;故①正确;根据相似三角形的性质得到S△BCE=36;故②正确;根据三角形的面积公式得到S△ABE=12,故③正确;由于△AEF与△ADC只有一个角相等,于是得到△AEF与△ACD不一定相似,故④错误.
解:∵在 ABCD中,AO=AC,
∵点E是OA的中点,
∴AE=CE,
∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵AD=BC,
∴AF=AD,
∴=;故①正确;
∵S△AEF=4, =()2=,
∴S△BCE=36;故②正确;
∵==,
∴=,
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故选D.
、填空题
解:=
+1=
=
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值()叫做黄金比.
解:由题意得:则AC=BD=AB=80×=40-40;
AD=AB-BD=80-(40-40)=120-40;
DC=AB-2AD=80-160.
故本题答案为:40-40,80-160.
【分析】根据平行线分线段成比例定理列出比例式,计算即可.
解:∵AB∥CD,
∴==,即=,
解得,AO=4,
故答案为:4.
【分析】根据相似三角形面积的比等于相似比的平方求出相似比,根据似三角形周长的比等于相似比得到答案.
解:∵两个相似三角形的面积比为1:4,
∴这两个相似三角形的相似比为1:2,
∴这两个相似三角形的周长比是1:2,
故答案为:1:2.
【分析】结论:DF∥AC,或∠BFD=∠A.根据相似三角形的判定方法一一证明即可.
解:DF∥AC,或∠BFD=∠A.
理由:∵∠A=∠A, ==,
∴△ADE∽△ACB,
∴①当DF∥AC时,△BDF∽△BAC,
∴△BDF∽△EAD.
②当∠BFD=∠A时,∵∠B=∠AED,
∴△FBD∽△AED.
故答案为DF∥AC,或∠BFD=∠A.
【分析】若A,D,E为顶点的三角形与△ABC相似时,则=或=,分情况进行讨论后即可求出AE的长度.
解:当=时,
∵∠A=∠A,
∴△AED∽△ABC,
此时AE===;
当=时,
∵∠A=∠A,
∴△ADE∽△ABC,
此时AE===;
故答案为:或.
【分析】把B的横纵坐标分别乘以﹣得到B′的坐标.
解:由题意得:△A′OB′与△AOB的相似比为2:3,
又∵B(3,﹣2)
∴B′的坐标是[3×,﹣2×],即B′的坐标是(﹣2,);
故答案为:(﹣2,).
、解答题
【分析】根据比例的性质(两内项之积等于两外项之积),可设=t,然后用t分别表示a、b、c,并将其代入所求的代数式,消去未知数t.
解:设=t,
∴,
解得,,
∴==.
【分析】根据把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值( )叫做黄金比即可得出C点所处位置.
解:距点A至少是1-≈0.4或距点B至少是1-≈0.4,
故最佳位置C在距A点或B点AB处,
如图所示:
【分析】由于BC是△ABC与△DBC的公共边,且AB∥EF∥CD,利用平行线分线段成比例的定理,可求EF.
解:在△ABC中,因为EF∥AB,
所以EF:AB=CF:CB①,
同样,在△DBC中有EF:CD=BF:CB②,
①+②得EF:AB+EF:CD=CF:CB+BF:CB=1③.
设EF=x厘米,又已知AB=6厘米,CD=9厘米,代入③得
x:6+x:9=1,
解得x=.
故EF=厘米.
【分析】由AM⊥EC,CD⊥EC,EA=MA,可得EC=CD,再由BN⊥EC,可得BN∥CD,进而可得△ABN∽△ACD,根据相似三角形对应边成比例的性质列式求解.
解:设CD的长为 m.
∵ AM⊥EC,CD⊥EC,BN⊥EC,
∴ MA∥CD,BN∥CD.
又EA=MA,
∴ EC=CD=.
由BN∥CD可得△ABN∽△ACD,
∴ ,即,解得=6.125≈6.1.
∴ 路灯高CD约为6.1 m.
【分析】由于△ADE与△BDE是等高的三角形,可得=,同理亦可得,,再由平行线分线段成比例的性质可得M与S的关系,进而即可求解.
证明:由于△ADE与△BDE是等高的三角形,
故
又△ADE与△ABE也是等高三角形,
故(2)
同理,(3)
又DE∥BC,故,设此比值为x
将(1),(2),(3)式相乘,
得
即
法一:展开得Sx2-Sx+M=0有实根,
故△=S2-4SM≥0
解之得
法二:由.
【分析】根据相似三角形的判定与性质,可得答案.
解:∵DE⊥AB,
∴∠BED=90°,
又∠C=90°,
∴∠BED=∠C.
又∠B=∠B,
∴△BED∽△BCA,
∴=,
∴DE===4
【分析】 (1)从图中得到AC=3,CD=2,BC=6,CE=4,∠ACB=∠DCE=90°,故有,根据两边对应成比例且夹角相等的两三角形相似得到△ACB∽△DCE;
(2)先由相似三角形的对应角相等得出∠ABC=∠DEC,又∠BDF=∠EDC,得出△DFB∽△DCE,再根据相似三角形的面积比等于相似比的平方即可求解.
(1)证明:∵AC=3,CD=2,BC=6,CE=4,
∴,,
∴,
又∵∠ACB=∠DCE=90°,
∴△ACB∽△DCE;
(2)解:在Rt△DCE中,DE2=DC2+CE2=22+42=20.
∵△ACB∽△DCE,
∴∠ABC=∠DEC,
又∵∠BDF=∠EDC,
∴△DFB∽△DCE.
∴S△DFB:S△DCE=DB2:DE2=16:20=4:5.
【分析】(1)由勾股定理求PD,根据AM=AF=PF-PA=PD-PA,DM=AD-AM求解;
(2)由(1)计算的数据进行证明;
(3)根据(2)的结论得:=,根据黄金分割点的概念,则点M是AD的黄金分割点.
解:(1)在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF-PA=PD-PA=-1,
DM=AD-AM=2-(-1)=3-;
(2)证明:∵AM2=(-1)2=6-2,AD DM=2(3-)=6-2,
∴AM2=AD DM;
(3)点M是AD的黄金分割点.理由如下:
∵AM2=AD DM,
∴═=,
∴点M是AD的黄金分割点.
(
第
2
页
共
2
页
)版权所有@21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
21世纪教育网 –中小学教育资源及组卷应用平台
图形的相似单元检测A卷
姓名:__________班级:__________学号:__________
、选择题(本大题共12小题)
若≠0,则=( )
A. B. C. D.无法确定
如果点C为线段AB的黄金分割点,且AC>BC,则下列各式不正确的是( )
A.AB:AC=AC:BC B.AC= C.AB= D.BC≈0.618AB
如图,已知AB∥CD∥EF,那么下列结论正确的是()
A. B. C. D.
已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )
A.1:4 B.4:1 C.1:2 D.2:1
如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A.6 B.12 C.18 D.24
如图,路灯AB的高度为8米,树CD与路灯的水平距离为4米,则得树在灯光下的影长DE为3米,则树高( )
A.4米 B.6米 C.米 D.米
如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
下列各组图形不一定相似的是( )
A.两个等腰直角三角形, B.各有一个角是100°的两个等腰三角形
C.两个矩形 D.各有一个角是50°的两个直角三角形
如图所示,在 ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF︰FC等于( )
A.3︰2 B.3︰1 C.1︰1 D.1︰2
如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )
A.1.5米 B.2.3米 C.3.2米 D.7.8米
CD是△ABC中AB边上的高,已知CD=6,DA=3,DB=12,则( )
A.CA2+BC2=AB2 B.∠CAB=∠CBD C.∠CAB>∠ACB D.∠ACD=∠BCD
如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① =;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②③
、填空题(本大题共7小题)
已知=,则=________.
如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点(即AC是AB与BC的比例中项),支撑点D是靠近点A的黄金分割点,则AC= cm,DC= cm.
已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO= .
若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是 .
如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: ,可以使得△FDB与△ADE相似.(只需写出一个)
在△ABC在,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE= 时,以A.D、E为顶点的三角形与△ABC相似.
如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是 .
、解答题(本大题共8小题)
已知:,求代数式的值.
实践证明,节目主持人站在舞台的黄金分割点处音响效果及审美效果最好.如下图,假设线段AB为舞台前沿,你能为主持人找出一个最佳位置C吗?
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图所示,当李明走到点A时,张龙测得李明直立时身高AM与其影子长AE正好相等;接着李明沿AC方向继续向前走,到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立的身高为1.75 m.求路灯的高度CD.(结果精确到0.1 m)
已知任意三角形ABC,其面积为S.作BC的平行线与AB、AC分别交于D、E.设三角形BDE的面积为M,求证:M≤.
如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
如图,在9×10的正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;
(2)求△DFB和△DCE的面积比.
以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)求证:AM2=AD DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
答案解析
、选择题
【分析】设比值为k,然后用k表示出a、b、c,再代入算式进行计算即可求解.
解:设=k,
则a=2k,b=3k,c=4k,
∴==.
故选B.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值( )叫做黄金比.
解:∵AC>BC,
∴AC是较长的线段,
根据黄金分割的定义可知:AB:AC=AC:BC,AC=AB,AB=,AC≈0.618AB.
故选D.
【分析】 已知AB∥CD∥EF,根据平行线分线段成比例定理,对各项进行分析即可.
解:∵AB∥CD∥EF,
∴=.
故选D.
【分析】利用相似三角形面积之比等于相似比的平方计算即可.
解:∵△ABC∽△DEF,且相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选A
【分析】根据线段中点的性质求出AD=AB、AE=AC的长,根据三角形中位线定理求出DE=AB,根据三角形周长公式计算即可.
解:∵D、E分别是AB、AC的中点,
∴AD=AB,AE=AC,DE=BC,
∴△ABC的周长=AB+AC+BC=2AD+2AE+2DE=2(AD+AE+DE)=2×6=12.
故选B.
【分析】由于人和地面是垂直的,即和路灯平行,构成相似三角形.根据对应边成比例,列方程解答即可.
解:因为CD∥AB,
∴△AEB∽△CED,
∴AB:CD=BE:ED,
即8:CD=7:3
解得:AB=m.
故选D.
【分析】先求出位似比,根据位似比等于相似比,再由相似三角形的面积比等于相似比的平方即可.
解:由位似变换的性质可知,A′B′∥AB,A′C′∥AC,
∴△A′B′C′∽△ABC.
∵△A'B'C'与△ABC的面积的比4:9,
∴△A'B'C'与△ABC的相似比为2:3,
∴=
故选:A.
【分析】根据相似图形的定义,对应边成比例,对应角相等对各选项分析判断。
解:A.两个等腰直角三角形,对应边成比例,对应角相等,符合定义,一定相似,故正确;
B、各有一个角是100°的两个等腰三角形,100°的角一定是顶角,其余两角一定相等,故一定相似,故正确;
C、两个矩形,四个角都是直角,但四条边不一定对应成比例,不一定相似,故错误;
D、各有一个角是50°的两个直角三角形,都有一个直角,根据两角对应相等,两三角形相似,故正确。
故选C
【分析】根据平行四边形的性质和相似三角形的判定与性质求解
解: ∵ ABCD,故AD∥BC,
∴△DEF∽△BCF,
∴DE:BC=EF:FC,
∵点E是边AD的中点,
∴AE=DE=AD,
∴EF:FC=1:2.
故选D.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
解: 设树高为x米,
因为,
所以
解得:x=3.2.
故选C.
【分析】画出图形,根据CD、DA计算AC,根据DB、DA计算AB,解直角△ACD、直角△CBD则可得A选项正确.
解:CA2+BC2=AD2+CD2+BD2+CD2=144+36+36+9=225,
AB=DA+DB=15,AB2=225,
∴CA2+BC2=AB2=225,(A选项正确)
且AD=3,CD=6,BD=12,CD⊥AB,
∴△BCD∽△CAD,
∠ACD=∠CBD,∠BCD=∠CAD,(故B、D选项错误),
在△ABC中,AB>BC,
∠CAB<∠ACB,(故C选项错误).
故选A.
【分析】根据平行四边形的性质得到AE=CE,根据相似三角形的性质得到==,等量代换得到AF=AD,于是得到=;故①正确;根据相似三角形的性质得到S△BCE=36;故②正确;根据三角形的面积公式得到S△ABE=12,故③正确;由于△AEF与△ADC只有一个角相等,于是得到△AEF与△ACD不一定相似,故④错误.
解:∵在 ABCD中,AO=AC,
∵点E是OA的中点,
∴AE=CE,
∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵AD=BC,
∴AF=AD,
∴=;故①正确;
∵S△AEF=4, =()2=,
∴S△BCE=36;故②正确;
∵==,
∴=,
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故选D.
、填空题
解:=
+1=
=
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值()叫做黄金比.
解:由题意得:则AC=BD=AB=80×=40-40;
AD=AB-BD=80-(40-40)=120-40;
DC=AB-2AD=80-160.
故本题答案为:40-40,80-160.
【分析】根据平行线分线段成比例定理列出比例式,计算即可.
解:∵AB∥CD,
∴==,即=,
解得,AO=4,
故答案为:4.
【分析】根据相似三角形面积的比等于相似比的平方求出相似比,根据似三角形周长的比等于相似比得到答案.
解:∵两个相似三角形的面积比为1:4,
∴这两个相似三角形的相似比为1:2,
∴这两个相似三角形的周长比是1:2,
故答案为:1:2.
【分析】结论:DF∥AC,或∠BFD=∠A.根据相似三角形的判定方法一一证明即可.
解:DF∥AC,或∠BFD=∠A.
理由:∵∠A=∠A, ==,
∴△ADE∽△ACB,
∴①当DF∥AC时,△BDF∽△BAC,
∴△BDF∽△EAD.
②当∠BFD=∠A时,∵∠B=∠AED,
∴△FBD∽△AED.
故答案为DF∥AC,或∠BFD=∠A.
【分析】若A,D,E为顶点的三角形与△ABC相似时,则=或=,分情况进行讨论后即可求出AE的长度.
解:当=时,
∵∠A=∠A,
∴△AED∽△ABC,
此时AE===;
当=时,
∵∠A=∠A,
∴△ADE∽△ABC,
此时AE===;
故答案为:或.
【分析】把B的横纵坐标分别乘以﹣得到B′的坐标.
解:由题意得:△A′OB′与△AOB的相似比为2:3,
又∵B(3,﹣2)
∴B′的坐标是[3×,﹣2×],即B′的坐标是(﹣2,);
故答案为:(﹣2,).
、解答题
【分析】根据比例的性质(两内项之积等于两外项之积),可设=t,然后用t分别表示a、b、c,并将其代入所求的代数式,消去未知数t.
解:设=t,
∴,
解得,,
∴==.
【分析】根据把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值( )叫做黄金比即可得出C点所处位置.
解:距点A至少是1-≈0.4或距点B至少是1-≈0.4,
故最佳位置C在距A点或B点AB处,
如图所示:
【分析】由于BC是△ABC与△DBC的公共边,且AB∥EF∥CD,利用平行线分线段成比例的定理,可求EF.
解:在△ABC中,因为EF∥AB,
所以EF:AB=CF:CB①,
同样,在△DBC中有EF:CD=BF:CB②,
①+②得EF:AB+EF:CD=CF:CB+BF:CB=1③.
设EF=x厘米,又已知AB=6厘米,CD=9厘米,代入③得
x:6+x:9=1,
解得x=.
故EF=厘米.
【分析】由AM⊥EC,CD⊥EC,EA=MA,可得EC=CD,再由BN⊥EC,可得BN∥CD,进而可得△ABN∽△ACD,根据相似三角形对应边成比例的性质列式求解.
解:设CD的长为 m.
∵ AM⊥EC,CD⊥EC,BN⊥EC,
∴ MA∥CD,BN∥CD.
又EA=MA,
∴ EC=CD=.
由BN∥CD可得△ABN∽△ACD,
∴ ,即,解得=6.125≈6.1.
∴ 路灯高CD约为6.1 m.
【分析】由于△ADE与△BDE是等高的三角形,可得=,同理亦可得,,再由平行线分线段成比例的性质可得M与S的关系,进而即可求解.
证明:由于△ADE与△BDE是等高的三角形,
故
又△ADE与△ABE也是等高三角形,
故(2)
同理,(3)
又DE∥BC,故,设此比值为x
将(1),(2),(3)式相乘,
得
即
法一:展开得Sx2-Sx+M=0有实根,
故△=S2-4SM≥0
解之得
法二:由.
【分析】根据相似三角形的判定与性质,可得答案.
解:∵DE⊥AB,
∴∠BED=90°,
又∠C=90°,
∴∠BED=∠C.
又∠B=∠B,
∴△BED∽△BCA,
∴=,
∴DE===4
【分析】 (1)从图中得到AC=3,CD=2,BC=6,CE=4,∠ACB=∠DCE=90°,故有,根据两边对应成比例且夹角相等的两三角形相似得到△ACB∽△DCE;
(2)先由相似三角形的对应角相等得出∠ABC=∠DEC,又∠BDF=∠EDC,得出△DFB∽△DCE,再根据相似三角形的面积比等于相似比的平方即可求解.
(1)证明:∵AC=3,CD=2,BC=6,CE=4,
∴,,
∴,
又∵∠ACB=∠DCE=90°,
∴△ACB∽△DCE;
(2)解:在Rt△DCE中,DE2=DC2+CE2=22+42=20.
∵△ACB∽△DCE,
∴∠ABC=∠DEC,
又∵∠BDF=∠EDC,
∴△DFB∽△DCE.
∴S△DFB:S△DCE=DB2:DE2=16:20=4:5.
【分析】(1)由勾股定理求PD,根据AM=AF=PF-PA=PD-PA,DM=AD-AM求解;
(2)由(1)计算的数据进行证明;
(3)根据(2)的结论得:=,根据黄金分割点的概念,则点M是AD的黄金分割点.
解:(1)在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF-PA=PD-PA=-1,
DM=AD-AM=2-(-1)=3-;
(2)证明:∵AM2=(-1)2=6-2,AD DM=2(3-)=6-2,
∴AM2=AD DM;
(3)点M是AD的黄金分割点.理由如下:
∵AM2=AD DM,
∴═=,
∴点M是AD的黄金分割点.
(
第
2
页
共
2
页
)版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
