第4章 锐角三角函数单元检测B卷

21世纪教育网 –中小学教育资源及组卷应用平台
锐角三角函数单元检测B卷
姓名：__________班级：__________学号：__________
1 、选择题（本大题共12小题）
在△ABC中，∠C＝90°，AC=，AB=，则cosB的值为( )
A． B． C． D．
若α是锐角，且cosα=0.7，则（ ）
A．0°＜α＜30° B．30°≤α＜45° C．45°＜α＜60° D．60°≤α＜90°
在△ABC中，，那么△ABC是（ ）
A．钝角三角形； B．直角三角形； C．锐角三角形； D．等腰三角形
如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm的绑绳EF，，则“人字梯”的顶端离地面的高度AD是（ ）
A．144cm B．180cm C．240cm D．360cm
已知∠A为锐角，且tanA=，则∠A的取值范围是（ ）
A．0°＜∠A＜30° B．30°＜∠A＜45° C．45°＜∠A＜60° D．60°＜∠A＜90°
甲、乙、丙三人放风筝，各人放出的风筝线长分别为60m、50m、40m，线与地平面所成的角分别为30°、45°、60°，假设风筝线近似看作是拉直的，则所放风筝最高的是（ ）
A．甲 B．乙 C．丙 D．不能确定
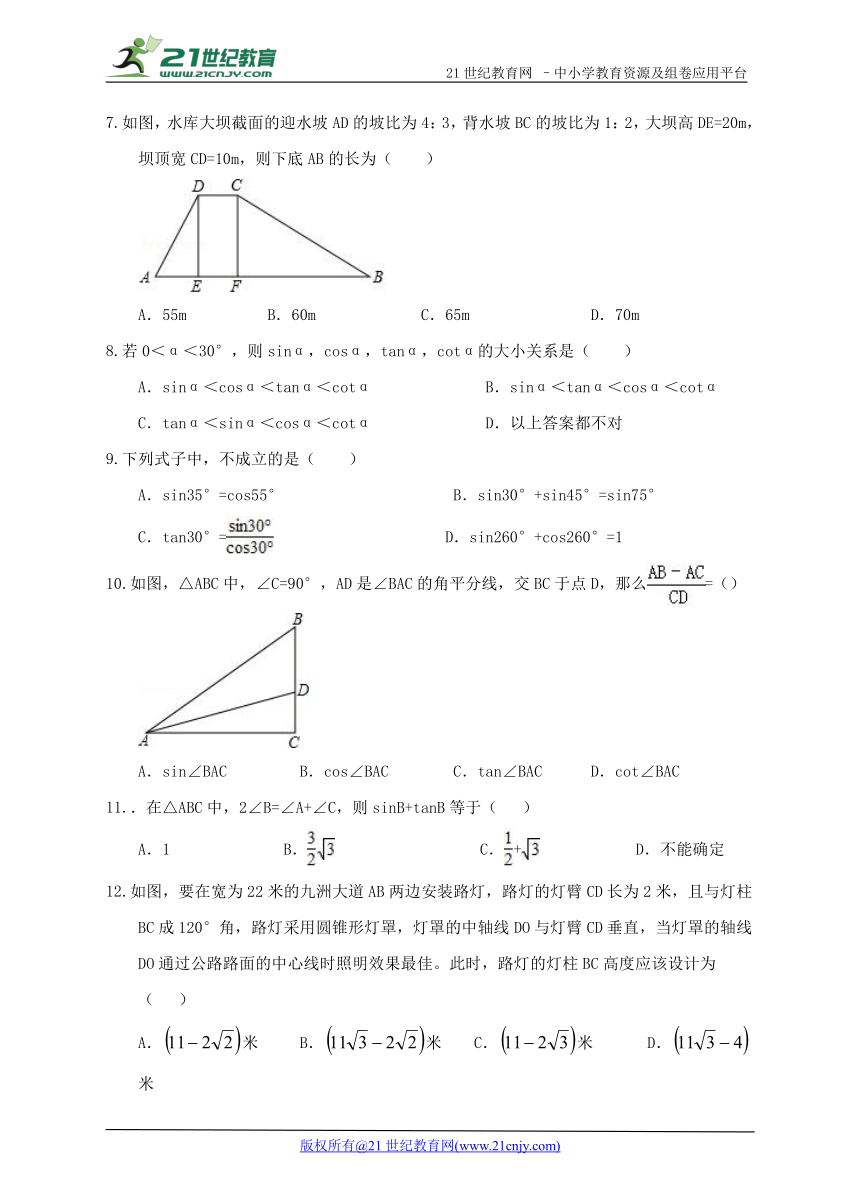
如图，水库大坝截面的迎水坡AD的坡比为4：3，背水坡BC的坡比为1：2，大坝高DE=20m，坝顶宽CD=10m，则下底AB的长为（　　）
A．55m B．60m C．65m D．70m
若0＜α＜30°，则sinα，cosα，tanα，cotα的大小关系是（ ）
A．sinα＜cosα＜tanα＜cotα B．sinα＜tanα＜cosα＜cotα
C．tanα＜sinα＜cosα＜cotα D．以上答案都不对
下列式子中，不成立的是（ ）
A．sin35°=cos55° B．sin30°+sin45°=sin75°
C．tan30°= D．sin260°+cos260°=1
如图，△ABC中，∠C=90°，AD是∠BAC的角平分线，交BC于点D，那么=（）
A．sin∠BAC B．cos∠BAC C．tan∠BAC D．cot∠BAC
．在△ABC中，2∠B=∠A+∠C，则sinB+tanB等于（ ）
A．1 B． C．+ D．不能确定
如图，要在宽为22米的九洲大道AB两边安装路灯，路灯的灯臂CD长为2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的中轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳。此时，路灯的灯柱BC高度应该设计为 （ ）
A．米 B．米 C．米 D．米
2 、填空题（本大题共6小题）
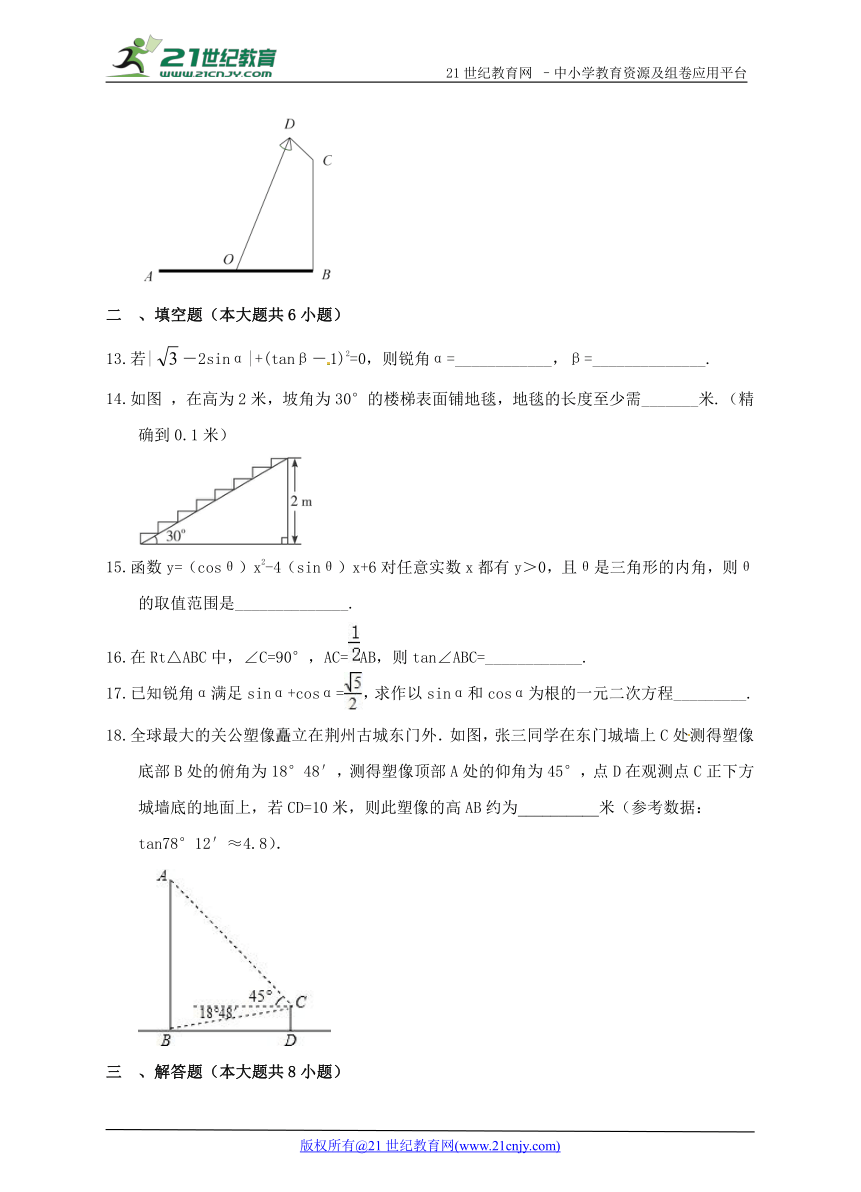
若|－2sinα|+(tanβ－1)2=0，则锐角α=____________，β=______________.
如图 ，在高为2米，坡角为30°的楼梯表面铺地毯，地毯的长度至少需_______米.（精确到0.1米）
( http: / / www..cn / )
函数y=（cosθ）x2-4（sinθ）x+6对任意实数x都有y＞0，且θ是三角形的内角，则θ的取值范围是______________.
在Rt△ABC中，∠C=90°，AC=AB，则tan∠ABC=____________.
已知锐角α满足sinα+cosα=，求作以sinα和cosα为根的一元二次方程_________.
全球最大的关公塑像矗立在荆州古城东门外．如图，张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′，测得塑像顶部A处的仰角为45°，点D在观测点C正下方城墙底的地面上，若CD=10米，则此塑像的高AB约为__________米（参考数据：tan78°12′≈4.8）．
3 、解答题（本大题共8小题）
计算：﹣12017﹣丨1﹣丨+×（）﹣2+0．
计算：sin45°+sin2α+cos2α+
求下列各式的值：
（1）a、b、c是△ABC的三边，且满足a2=（c+b）（c-b）和4c-5b=0，求cosA+cosB的值；
（2）已知A为锐角，且tanA=，求sin2A+2sinAcosA+cos2A的值．
如图，Rt△中，，，为上一点，且，若，求的长．
如图，已知∠ABC和射线BD上一点P（点P与点B不重合），且点P到BA．BC的距离为PE、PF．
（1）若∠EBP=40°，∠FBP=20°，PB=m，试比较PE、PF的大小；
（2）若∠EBP=α，∠FBP=β，α，β都是锐角，且α＞β．试判断PE、PF的大小，并给出证明．
如图，MN表示一段笔直的高架道路，线段AB表示高架道路旁的一排居民楼．已知点A到MN的距离为15米，BA的延长线与MN相交于点D，且∠BDN＝30°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．
(1)过点A作MN的垂线，垂足为点H．如果汽车沿着从M到N的方向在MN上行驶，当汽车到达点P处时，噪音开始影响这一排的居民楼，那么此时汽车与点H的距离为多少米？
(2)降低噪音的一种方法是在高架道路旁安装隔音板．当汽车行驶到点Q时，它与这一排居民楼的距离QC为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？(精确到1米) (参考数据：≈1.7)
如图，在 ABCD中 过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．
（1）求证：△ABF∽△BEC；
（2）若AD=5，AB=8，sinD=，求AF的长．
如图，点A（m，4），B（﹣4，n）在反比例函数y=（k＞0）的图象上，经过点A．B的直线与x轴相交于点C，与y轴相交于点D．
（1）若m=2，求n的值；
（2）求m+n的值；
（3）连接OA．OB，若tan∠AOD+tan∠BOC=1，求直线AB的函数关系式．
答案解析
1 、选择题
解：由勾股定理,得BC=，
∴cosB=.
答案：C
【分析】在锐角三角函数中，余切值都是随着角的增大而减小．cos30°=，cos45°=，故知α的范围．
解：∵在锐角三角函数中，余切值都是随着角的增大而减小，
又知cos60°=，cos45°=，
故45°＜α＜60°．
故选C．
【分析】先根据△ABC中，tanA=1，cotB=求出∠A及∠B的度数，再由三角形内角和定理求出∠C的度数，进而可判断出三角形的形状．
∵△ABC中，tanA=1，cotB=，
∴∠A=45°，∠B=30°，
∴∠C=180°-∠A-∠B=180°-45°-30°=105°，
∴△ABC是钝角三角形．
故选A.
解：由题平面图如图所示, ∵EF=60cm，,
故选B
【分析】判断出所给的正切值在最接近的哪两个锐角的正切值之间，即可得到正确选项．
解：∵＜＜1，
∴30°＜tanA＜45°．
故选B
6. 【分析】易得风筝线与所放风筝距离地面的高度为直角三角形的斜边和相应度数所对的对边，利用相应度数的正弦值可得所放风筝的高度，比较即可．
解：∵各人放出的风筝线长分别为60m、50m、40m，线与地平面所成的角分别为30°、45°、60°，
∴相应的高度分别为60×sin30°=30=m；
50×sin45°=25=m；
40×sin60°=20=m；
∴乙同学放的风筝最高，
故选B．
【分析】利用坡比的比值关系，求出AE与BF的长度即可得出下底的长．
解：∵DE=20m，DE：AE=4：3，
∴AE=15m，
∵CF=DE=20m，CF：BF=1：2，
∴BF=40m，
∴AB=AE+EF+BF=15+10+40=65m．
故选C．
【分析】根据三角函数的增减性即可作出判断．
解：由它们的取值范围可得：sinα＜cosα＜cotα，且tanα＜cosα，α为锐角时，sinα＜tanα恒成立．
∴sinα＜tanα＜cosα＜cotα．
故选D
【分析】根据互余两角三角函数的关系，特殊角的三角函数值及锐角三角函数的定义，同角三角函数的关系进行判断即可．
解：A．根据一个角的正弦值等于这个角的余角的余弦值，可知sin35°=cos55°，正确，不符合题意，故本选项错误；
B、因为sin30°+sin45°=+＞1，sin75°＜1，所以sin30°+sin45°=sin75°，错误，符合题意，故本选正确；
C、根据一个角的正切值等于这个角的正弦与余弦的比，可知tan30°=，正确，不符合题意，故本选项错误；
D、根据同一个角的正弦与余弦的平方和等于1，可知sin260°+cos260°=1，正确，不符合题意，故本选项错误．
故选B．．
【分析】过点D作DE⊥AB于E，由角的平分线的性质得CD=DE，证明AB﹣AC=BE，则=tan∠BDE，再证明∠BAC=∠BDE即可．
解：过点D作DE⊥AB于E．
∵AD是∠BAC的角平分线，DE⊥AB于E，DC⊥AC于C，
∴CD=DE．
∴Rt△ADE≌Rt△ADC（HL）
∴AE=AC．
∴==tan∠BDE．
∵∠BAC=∠BDE，（同角的余角相等）
∴=tan∠BDE=tan∠BAC，
故选C．
【分析】根据已知和三角形内角和定理得出3∠B=180°，求出∠B=60°，根据特殊角的三角函数值即可求出答案．
解：∵2∠B=∠A+∠C，∠B+∠A+∠C=180°，
∴3∠B=180°，
∴∠B=60°，
∴sinB+tanB=sin60°+tan60°=+=，
故选B．
过D做DE⊥AB交AB于点E，过C做CF⊥DE交DE于点F．
∵∠DCB=120°，CB⊥AB，OD⊥CD，
∴∠DOB=360°-∠DCB-∠CBO-∠ODC=360°-120°-90°-90°=60°，即∠DCF=30°
∴ ，
∴，∴
∴ ，
∴
故选D
2 、填空题
13 解：由题意得sinα=,tanβ=1，
∴α=60°，β=45°.
答案：60° 45°
【分析】由题意得，地毯的总长度至少为（AC+BC）．在△ABC中已知一边和一个锐角，满足解直角三角形的条件，可求出AC的长．进而求得地毯的长度．
解：由题意得：地毯的竖直的线段加起来等于BC，水平的线段相加正好等于AC，
即地毯的总长度至少为（AC+BC）．
在Rt△ABC中，∠A=30°，BC=2m，∠C=90度．
∵tanA=，
∴AC=BC÷tan30°=2（m）．
∴AC+BC=2+2≈2×1.73+2=5.46≈5.5（m）．
答：地毯的长度至少需5.5m．
【分析】因为cosθ＞0，所以只要△＜0，函数值恒为正．由△＜0，得到三角函数不等式，再把正弦转化为余弦，解不等式，最后利用三角函数的增减性求出θ的取值范围．
解：由题意得
即
（2cosθ-1）（cosθ+2）＞0，
解得，又因为0°＜θ＜180°
所以θ的取值范围为0°＜θ＜60°．
故答案为0°＜θ＜60°．
【分析】利用锐角三角函数关系得出∠B的值，即可得出答案．
解：如图所示：∵∠C=90°，AC=AB，
∴sinB=，
∴∠B=30°，
∴tan∠ABC=．
故答案为：．
【分析】先根据sinα+cosα=，求出sinα cosα=，再根据根与系数的关系即可得出答案．
解：∵锐角α满足sinα+cosα=，
∴（sinα+cosα）2=，
∴sin2α+cos2α+2sinα cosα=，
∴sinα cosα=，
∴以sinα和cosα为根的一元二次方程是x2-x=0．
故答案为：x2-x=0．
【分析】直接利用锐角三角函数关系得出EC的长，进而得出AE的长，进而得出答案．
解：如图所示：由题意可得：CE⊥AB于点E，BE=DC，
∵∠ECB=18°48′，
∴∠EBC=78°12′，
则tan78°12′===4.8，
解得：EC=48（m），
∵∠AEC=45°，则AE=EC，且BE=DC=10m，
∴此塑像的高AB约为：AE+EB=58（米）．
故答案为：58．
3 、解答题
【分析】直接利用绝对值的性质以及负指数幂的性质以及零指数幂的性质分别化简求出答案．
解：原式=﹣1﹣|1﹣×|+2×4+1
=﹣1﹣0+8+1
=8．
【分析】利用平方关系得到sin2α+cos2α=1，再将特殊角的三角函数值代入，即可求出式子的值．
解：原式=×+1+-，
=1+1+1-1，
=2．
【分析】（1）根据勾股定理的逆定理，判定这个三角形是直角三角形．再根据锐角三角函数的概念进行求解，也可以利用互为余角的三角函数关系式求解．
（2）根据tanA=，求出∠A=60°，再根据特殊角的三角函数值代入求值即可．
解：（1）由a2=（c+b）（c-b）得c2=a2+b2，所以∠C=90°，
由4c-5b=0得，
∴，，
∴；
（2）∵tanA=，∴∠A=60°，
∴原式=（）2+2××+（）2=+1．
解：过点作于点
∵在Rt△中，，，
∴设，，
由勾股定理得
∵
∴
∵，∴
∵Rt△中 ， ∴，
勾股定理得
∴
∴在Rt△中，由勾股定理得
【分析】（1）利用三角函数的定义，根据两个角的正弦的大小进行比较即可得到结果；
（2）运用两个角的正弦函数，根据正弦值的变化规律进行比较．
解：（1）在Rt△BPE中，sin∠EBP==sin40°
在Rt△BPF中，sin∠FBP==sin20°
又sin40°＞sin20°
∴PE＞PF；
（2）根据（1）得
sin∠EBP==sinα，sin∠FBP==sinβ
又∵α＞β
∴sinα＞sinβ
∴PE＞PF．
【分析】（1）连接PA．在直角△PAH中利用勾股定理来求PH的长度；
（2）由题意知，隔音板的长度是PQ的长度．通过解Rt△ADH、Rt△CDQ分别求得DH、DQ的长度，然后结合图形得到：PQ=PH+DQ﹣DH，把相关线段的长度代入求值即可．
解：（1）如图，连接PA．由题意知，AP=39m．在直角△APH中，PH===36（米）；
（2）由题意知，隔音板的长度是PQ的长度．
在Rt△ADH中，DH=AH cot30°=15（米）．
在Rt△CDQ中，DQ===78（米）．
则PQ=PH+HQ=PH+DQ﹣DH=36+78﹣15≈114﹣15×1.7=88.5≈89（米）．
答：高架道路旁安装的隔音板至少需要89米．
【分析】（1）由平行四边形的性质得出AB∥CD，AD∥BC，AD=BC，得出∠D+∠C=180°，∠ABF=∠BEC，证出∠C=∠AFB，即可得出结论；
（2）由勾股定理求出BE，由三角函数求出AE，再由相似三角形的性质求出AF的长．
（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，AD=BC，
∴∠D+∠C=180°，∠ABF=∠BEC，
∵∠AFB+∠AFE=180°，
∴∠C=∠AFB，
∴△ABF∽△BEC；
（2）解：∵AE⊥DC，AB∥DC，
∴∠AED=∠BAE=90°，
在Rt△ABE中，根据勾股定理得：BE===4，
在Rt△ADE中，AE=AD sinD=5×=4，
∵BC=AD=5，
由（1）得：△ABF∽△BEC，
∴，即，
解得：AF=2．
∵△ADF∽△DEC，
【分析】（1）先把A点坐标代入y=求出k的值得到反比例函数解析式为y=，然后把B（﹣4，n）代入y=可求出n的值；
（2）利用反比例函数图象上点的坐标特征得到4m=k，﹣4n=k，然后把两式相减消去k即可得到m+n的值；
（3）作AE⊥y轴于E，BF⊥x轴于F，如图，利用正切的定义得到tan∠AOE==，tan∠BOF==，则+=1，加上m+n=0，于是可解得m=2，n=﹣2，从而得到A（2，4），B（﹣4，﹣2），然后利用待定系数法求直线AB的解析式．
解：（1）当m=2，则A（2，4），
把A（2，4）代入y=得k=2×4=8，
所以反比例函数解析式为y=，
把B（﹣4，n）代入y=得﹣4n=8，解得n=﹣2；
（2）因为点A（m，4），B（﹣4，n）在反比例函数y=（k＞0）的图象上，
所以4m=k，﹣4n=k，
所以4m+4n=0，即m+n=0；
（3）作AE⊥y轴于E，BF⊥x轴于F，如图，
在Rt△AOE中，tan∠AOE==，
在Rt△BOF中，tan∠BOF==，
而tan∠AOD+tan∠BOC=1，
所以+=1，
而m+n=0，解得m=2，n=﹣2，
则A（2，4），B（﹣4，﹣2），
设直线AB的解析式为y=px+q，
把A（2，4），B（﹣4，﹣2）代入得，解得，
所以直线AB的解析式为y=x+2．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)