西师大版六下数学一单元第4课时问题解决例2 课件
文档属性
| 名称 | 西师大版六下数学一单元第4课时问题解决例2 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-14 00:00:00 | ||
图片预览








文档简介
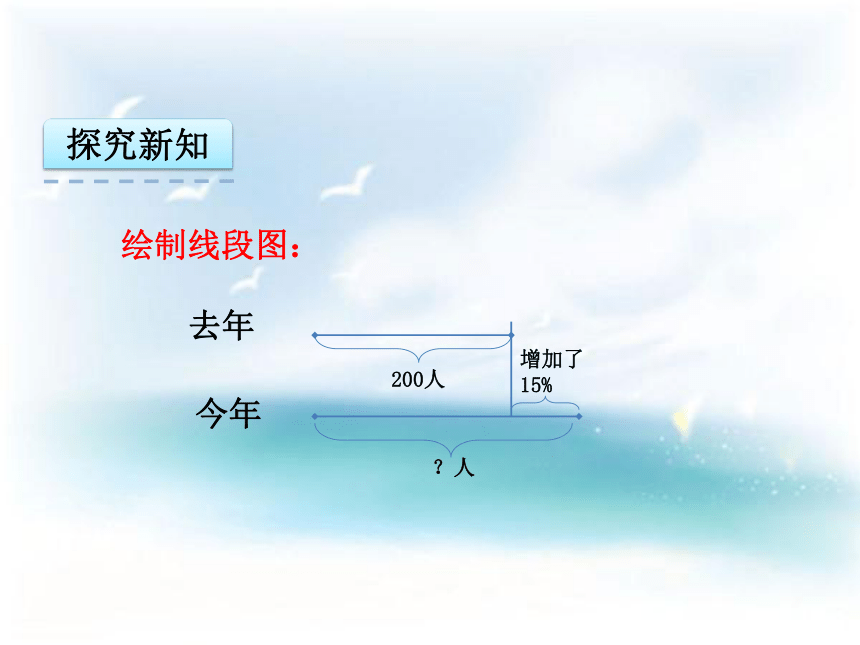
课件27张PPT。六年级 数学 下册西师版1.4 问题解决(例2)第1单元 百分数求比一个数多(或者少)百分之几的数是多少 让学生经历求比一个数多(或者少)百分之几的数是多少的过程,掌握这种题型的解题方法,能综合运用所学知识解决相关的实际问题。在解决问题中感受百分数与现实生活的联系,体会百分数的生活价值。复习导入某地区2006年前三季度农村居民人均现金收入比2005年同期增加百分之几。(用计算器计算,百分号前保留一位小数)理解题意:已知:2005年 2110元2006年 2762元问题:同期增加百分之几?复习导入某地区2006年前三季度农村居民人均现金收入比2005年同期增加百分之几。(用计算器计算,百分号前保留一位小数)解答过程: (2762-2110)÷2110=652÷2110=30.9%答:比2005年同期增加30.9%情境导入今年毕业生有多少人?探究新知今年的毕业生相当于去年毕业生人数的15%。探究新知去年今年200人?人增加了15%绘制线段图:探究新知200×(1+15%) =200 ×1.15=230(人)方法一:探究新知方法二:200 ×15% +200=30 +200答:今年的毕业生有230人。=230(人)探究新知如果明年的毕业生人数比今年减少10%,学校明年有毕业生多少人? 230 ×(1-10%)=230 ×0.9=207(人)方法一:方法二:230 ×10%=23(人)230 -23=207(人)答:学校明年有毕业生207人。探究新知如何求比一个数多(或者少)百分之几的数是多少?一个数+一个数×多的百分之几=所求的数或者一个数-一个数×少的百分之几=所求的数即时小练乙数是80,甲数比乙数多25%,甲数是多少?计算过程:80 +80 ×25%=80 +20=100答:甲数是100。即时小练甲数是100,乙数比甲数少20%,乙数是多少?计算过程:100 - 100 ×20%=100 - 20=80答:乙数是80。典题精讲一件衣服原价125元,如果先提价20%,后来又降价20%。那么这件衣服的价格还是125元吗?为什么?思路分析:“先提价20%”是指提高原价的20%,也就是相当于原价的120%,可以列出关系式:原价×( 1 +20%)求出第一次 变价的价格,“又降价20%”,是指降第一次提价后的20%,可以列出关系式:提价价格×(1 -20%),求出第二次变价的价格120元,再与125元对比,可以发现比125元少了。典题精讲一件衣服原价125元,如果先提价20%,后来又降价20%。那么这件衣服的价格还是125元吗?为什么?解答过程:125 +125×20%=125 +25=150(元)第1次变价:典题精讲一件衣服原价125元,如果先提价20%,后来又降价20%。那么这件衣服的价格还是125元吗?为什么?解答过程:150 - 150×20%=150 - 30=120(元)第2次变价:120元<125元典题精讲一件衣服原价125元,如果先提价20%,后来又降价20%。那么这件衣服的价格还是125元吗?为什么?答:这件衣服最后的价格是120元而不是125元,原因是衣服两次价格调动的单位“1”的量不相同,第一次变价的单位“1”是125元,第二次变价的单位“1”是150元。错题分析一种家电,提价5%后,又降价5%,现在的价格与原来相比( )。
A、与原价相同 B、比原价低 C、比原价高 D、不能确定A错误解答错题分析分析原因:此题关键是弄清楚提价5%与降价5%到底是提谁的价降谁的价,从题目当中仔细分析我们不难发现,提的是原价的5%,降的却是提价之后的5%,单位一的量已经发生了变化,所以现在的价格不可能与原价相同,选择A是错误的。错题分析一种家电,提价5%后,又降价5%,现在的价格与原来相比( )。
A、与原价相同 B、比原价低 C、比原价高 D、不能确定B正确解答学以致用一列火车原来每时行驶80km,现在速度提高了40%,这列火车现在每时行驶多少千米?解答过程:方法一: 80 × (1 + 40%)=80 × 1.4=112(千米)学以致用解答过程:方法二:80 ×40%=32(千米)80 +32=112(千米)答:这列火车现在每时行驶112千米。一列火车原来每时行驶80km,现在速度提高了40%,这列火车现在每时行驶多少千米?课堂 练习一本书原价是18元,现降价15%,这本书现价是多少元?解答过程: 18 ×(1 - 15%)=18 × 0.85=15.3(元)答:这本书现价是15.3元。课堂 总结这堂课我们学习了什么?你学会了什么?我们学习了求比一个数多或少百分之几的数是多少的问题。可以先算出相当于单位“1”的百分数。再用单位“1”的量乘以百分数,得到所求的数。谢谢
A、与原价相同 B、比原价低 C、比原价高 D、不能确定A错误解答错题分析分析原因:此题关键是弄清楚提价5%与降价5%到底是提谁的价降谁的价,从题目当中仔细分析我们不难发现,提的是原价的5%,降的却是提价之后的5%,单位一的量已经发生了变化,所以现在的价格不可能与原价相同,选择A是错误的。错题分析一种家电,提价5%后,又降价5%,现在的价格与原来相比( )。
A、与原价相同 B、比原价低 C、比原价高 D、不能确定B正确解答学以致用一列火车原来每时行驶80km,现在速度提高了40%,这列火车现在每时行驶多少千米?解答过程:方法一: 80 × (1 + 40%)=80 × 1.4=112(千米)学以致用解答过程:方法二:80 ×40%=32(千米)80 +32=112(千米)答:这列火车现在每时行驶112千米。一列火车原来每时行驶80km,现在速度提高了40%,这列火车现在每时行驶多少千米?课堂 练习一本书原价是18元,现降价15%,这本书现价是多少元?解答过程: 18 ×(1 - 15%)=18 × 0.85=15.3(元)答:这本书现价是15.3元。课堂 总结这堂课我们学习了什么?你学会了什么?我们学习了求比一个数多或少百分之几的数是多少的问题。可以先算出相当于单位“1”的百分数。再用单位“1”的量乘以百分数,得到所求的数。谢谢
