人教版八年级上册数学第12章12.1全等三角形 教案
文档属性
| 名称 | 人教版八年级上册数学第12章12.1全等三角形 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 479.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-15 10:13:26 | ||
图片预览

文档简介
《全等三角形》
本节课是新人教版义务教育课程标准实验教材数学八年级上册第十一章第一课时的内容,本章围绕全等三角形,主要学习全等三角形的有关概念和性质,三角形全等的条件以及角平分线的性质,学生在七年级教材中学过了线段、角、相交线等与三角形有关的知识和一些简单的说理内容,这为全等三角形的学习奠定了基础,并且在今后学习等腰三角形、直角三角形、线段的垂直平分线、角平分线等内容中都要通过证明两个三角形全等来加以解决。
【知识与能力目标】
1、了解全等形和全等三角形的概念,掌握全等三角形的性质。
2、能用符号正确表示两个三角形全等,能找出全等三角形的对应元素。
【过程与方法目标】
在图形变换以及实际操作的过程中发展学生的空间观念,培养学生的几何直觉,通过全等三角形有关概念的学习,提高学生数学概念的辨析能力,通过找出全等三角形的对应元素,培养学生的识图能力。
【情感态度价值观目标】
通过感受全等三角形的对应美激发学生热爱科学勇于探索的精神,通过自主学习的发展体验获取数学知识的感受,培养学生勇于创新,多方位审视问题的创造技巧,培养学生科学的学习态度及自信,互相尊重的健全人格。
【教学重点】
全等三角形的概念和性质.
【教学难点】
找出全等三角形的对应边、对应角.
多媒体课件、三角板。
一、新课导入
观察下列图案,指出这些图案中形状与大小相同的图形.
问题:你还能举出生活中一些实际例子吗?
探究:把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗?把三角尺和裁得的纸板放在一起能够完全重合吗?从同一张底片冲洗出来的两张尺寸相同的照片上的图形,放在一起也能够完全重合吗?
这些形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
能够完全重合的两个三角形叫做全等三角形。
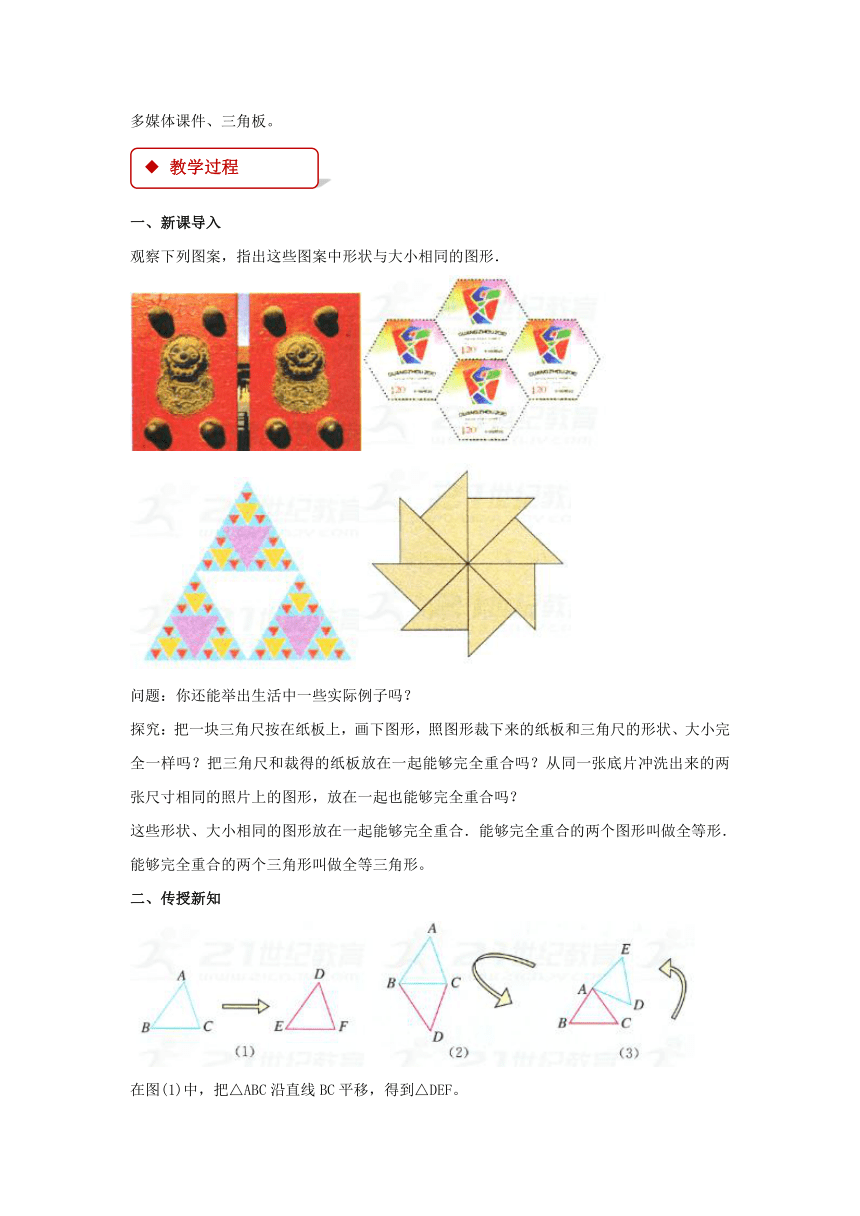
二、传授新知
在图(1)中,把△ABC沿直线BC平移,得到△DEF。
在图(2)中,把△ABC沿直线BC翻折180°,得到△DBC。
在图(3)中,把△ABC旋转后得到△ADE。
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即两图形全等.
“全等”用“≌”表示,读作“全等于”。
两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上,如全等时,点A和点D,点B和点E,点C和点F是对应顶点,记作。
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
观察下图,
可以得到全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等。
三、随堂练习
1、如图,△OCA
≌△OBD,点C
和点B,点A与点D是对应点,则下列结论错误的是(
D
).
(A)
∠COA
=∠BOD
;
(B)
∠A
=∠D
;
(C)
CA
=BD
;
(D)
OB
=OA
.
2、△ABN
≌△ACM,∠ABN
和∠ACM
是对应角,AB和AC
是对应边.则下列结论错误的是
(
C
)。
(A)∠AMC
=∠ANB
;
(B)∠BAN
=∠CAM
;
(C)BM
=MN
;
(D)AM
=AN
.
3、如图,△ABC
≌△CDA,AB
与CD,BC与DA
是对应边,则下列结论错误的是(
C
)。
(A)∠
BAC
=∠
DCA
;
(B)AB
//DC
;
(C)∠
BCA
=∠
DCA
;
(D)BC
//DA
.
4、如图,△EFG
≌△NMH,∠F
和∠M
是对应角。
(1)FG
与MH
平行吗?为什么?
(2)判断线段EH
与NG
的大小关系,并说明理由。
(1)平行;
(2)相等.
四、课堂小结
通过本节课学习,我们了解了全等的概念,发现了全等三角形的性质,并且利用性质可以找到两个全等三角形的对应元素,这也是这节课大家要重点掌握的。
略。
教材分析
教学目标
教学重难点
课前准备
教学过程
教学反思
本节课是新人教版义务教育课程标准实验教材数学八年级上册第十一章第一课时的内容,本章围绕全等三角形,主要学习全等三角形的有关概念和性质,三角形全等的条件以及角平分线的性质,学生在七年级教材中学过了线段、角、相交线等与三角形有关的知识和一些简单的说理内容,这为全等三角形的学习奠定了基础,并且在今后学习等腰三角形、直角三角形、线段的垂直平分线、角平分线等内容中都要通过证明两个三角形全等来加以解决。
【知识与能力目标】
1、了解全等形和全等三角形的概念,掌握全等三角形的性质。
2、能用符号正确表示两个三角形全等,能找出全等三角形的对应元素。
【过程与方法目标】
在图形变换以及实际操作的过程中发展学生的空间观念,培养学生的几何直觉,通过全等三角形有关概念的学习,提高学生数学概念的辨析能力,通过找出全等三角形的对应元素,培养学生的识图能力。
【情感态度价值观目标】
通过感受全等三角形的对应美激发学生热爱科学勇于探索的精神,通过自主学习的发展体验获取数学知识的感受,培养学生勇于创新,多方位审视问题的创造技巧,培养学生科学的学习态度及自信,互相尊重的健全人格。
【教学重点】
全等三角形的概念和性质.
【教学难点】
找出全等三角形的对应边、对应角.
多媒体课件、三角板。
一、新课导入
观察下列图案,指出这些图案中形状与大小相同的图形.
问题:你还能举出生活中一些实际例子吗?
探究:把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗?把三角尺和裁得的纸板放在一起能够完全重合吗?从同一张底片冲洗出来的两张尺寸相同的照片上的图形,放在一起也能够完全重合吗?
这些形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
能够完全重合的两个三角形叫做全等三角形。
二、传授新知
在图(1)中,把△ABC沿直线BC平移,得到△DEF。
在图(2)中,把△ABC沿直线BC翻折180°,得到△DBC。
在图(3)中,把△ABC旋转后得到△ADE。
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即两图形全等.
“全等”用“≌”表示,读作“全等于”。
两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上,如全等时,点A和点D,点B和点E,点C和点F是对应顶点,记作。
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
观察下图,
可以得到全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等。
三、随堂练习
1、如图,△OCA
≌△OBD,点C
和点B,点A与点D是对应点,则下列结论错误的是(
D
).
(A)
∠COA
=∠BOD
;
(B)
∠A
=∠D
;
(C)
CA
=BD
;
(D)
OB
=OA
.
2、△ABN
≌△ACM,∠ABN
和∠ACM
是对应角,AB和AC
是对应边.则下列结论错误的是
(
C
)。
(A)∠AMC
=∠ANB
;
(B)∠BAN
=∠CAM
;
(C)BM
=MN
;
(D)AM
=AN
.
3、如图,△ABC
≌△CDA,AB
与CD,BC与DA
是对应边,则下列结论错误的是(
C
)。
(A)∠
BAC
=∠
DCA
;
(B)AB
//DC
;
(C)∠
BCA
=∠
DCA
;
(D)BC
//DA
.
4、如图,△EFG
≌△NMH,∠F
和∠M
是对应角。
(1)FG
与MH
平行吗?为什么?
(2)判断线段EH
与NG
的大小关系,并说明理由。
(1)平行;
(2)相等.
四、课堂小结
通过本节课学习,我们了解了全等的概念,发现了全等三角形的性质,并且利用性质可以找到两个全等三角形的对应元素,这也是这节课大家要重点掌握的。
略。
教材分析
教学目标
教学重难点
课前准备
教学过程
教学反思
