第4章 图形的认识单元检测A卷
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
图形的认识单元检测A卷
姓名:__________班级:__________学号:__________
1 、选择题(本大题共12小题 )
谜语:干活两腿脚,一腿勤,一腿懒,一脚站,一脚转.打一数学学习用具,谜底为( )
A.量角器 B.直尺 C.三角板 D.圆规
如图给出的分别有射线、直线、线段,其中能相交的图形有( )
A. ①②③④ B. ① C. ②③④ D. ①③
OC是∠AOB内的一条射线,下列所给的条件中,不能判断OC是∠AOB的平分线的是( )
A.∠AOC+∠BOC=∠AOB B.∠AOC=∠AOB
C.∠AOB=2∠AOC D.∠AOC=∠BOC
如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是( )
A.40° B.70° C.70°或80° D.80°或140°
如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
A.BM=AB B.AM+BM=AB C.AM=BM D.AB=2AM
钟表上的分针经过24分钟,分针转过的角度是( )
A.120゜ B.144゜ C.150゜ D.90゜
平面上有三点A,B,C,如果AB=8,AC=5,BC=3,下列说法正确的是( )
A.点C在线段AB上 B.点C在线段AB的延长线上
C.点C在直线AB外 D.点C可能在直线AB上,也可能在直线AB外
张雷同学从A地出发沿北偏东50°的方向行驶到B地,再由B地沿南偏西20°的方向行驶到C地,则∠ABC的度数为( )
A.40° B.30° C.20° D.10°
下列语句正确的有( )
①射线AB与射线BA是同一条射线
②两点之间的所有连线中,线段最短
③连接两点的线段叫做这两点的距离
④欲将一根木条固定在墙上,至少需要2个钉子.
A.1个 B.2个 C.3个 D.4个
下列说法中正确的个数是( )
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的补角,那么它们相等;④锐角和钝角互补.
A. 1 B. 2 C. 3 D. 4
如图不能折叠成正方体的是( )
A. B. C. D.
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A.点C B.点D或点E
C.线段DE(异于端点) 上一点 D.线段CD(异于端点) 上一点
1 、填空题(本大题共8小题 )
开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为______.
如图,A.B之间是一座山,一条铁路要通过A.B两地,在A地测得B地在北偏东70°,如果A.B两地同时开工修建铁路,那么在B地应按______方向开凿,才能使铁路在山腹中准确接通.
如图,用一个平面去截一个长方体,截面是一个多边形,这个多边形的边数最多有____条.
已知∠A=51°23′,则∠A的余角的度数是__________________.
在朱自清的《春》中有描写春雨“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明 .
如图,直线AB、CD相交于点O,∠DOE=∠BOE,OF平分∠AOD,若∠BOE=28°,则∠EOF的度数为______ .
已知线段AB=2cm,延长AB到点C,使BC=4cm,D为AB的中点,则线段DC=____________.
已知线段AB=2 cm,延长AB到C点,使BC=AB,再延长BA到D点,使AD=2AC,M是线段BC的中点,N是线段AD的中点,则线段MN的长是 .
1 、解答题(本大题共8小题 )
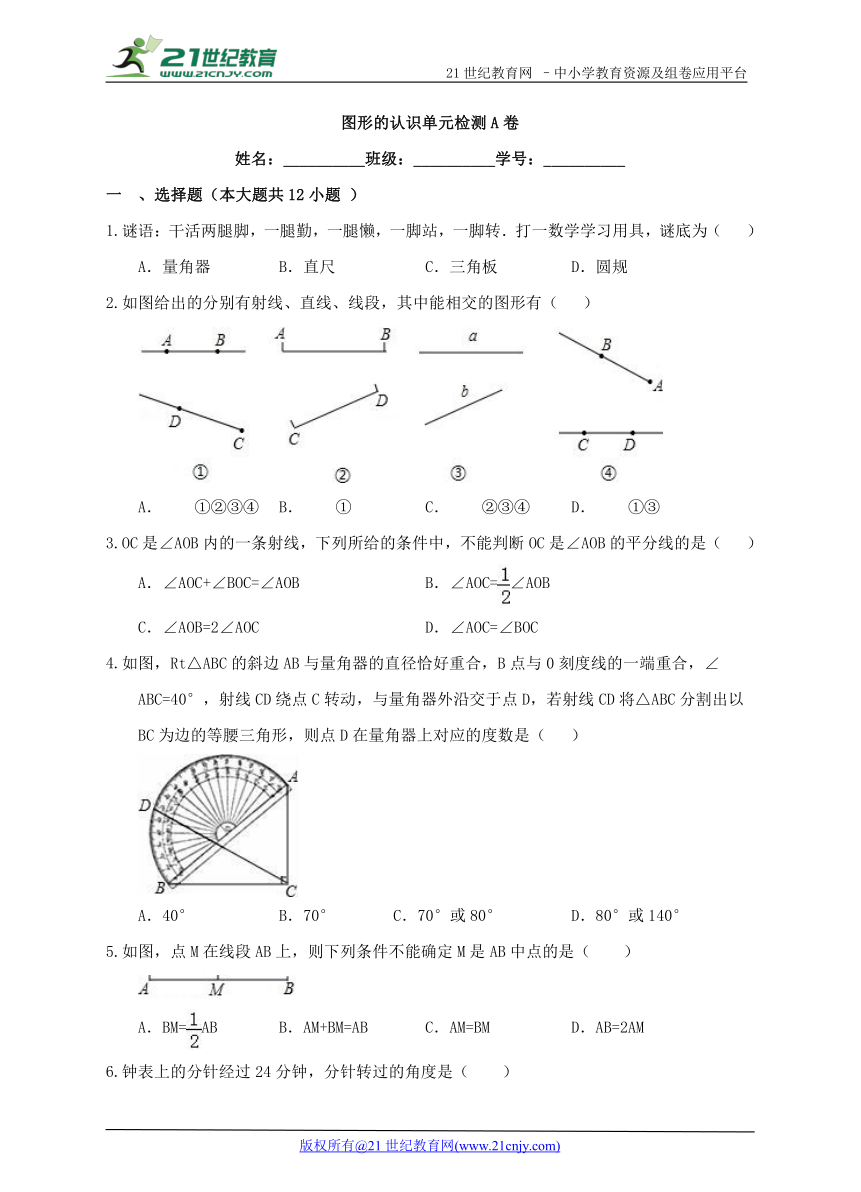
第一行的平面图形绕虚线旋转一周能得到第二行的一个几何体,请用线连接起来.
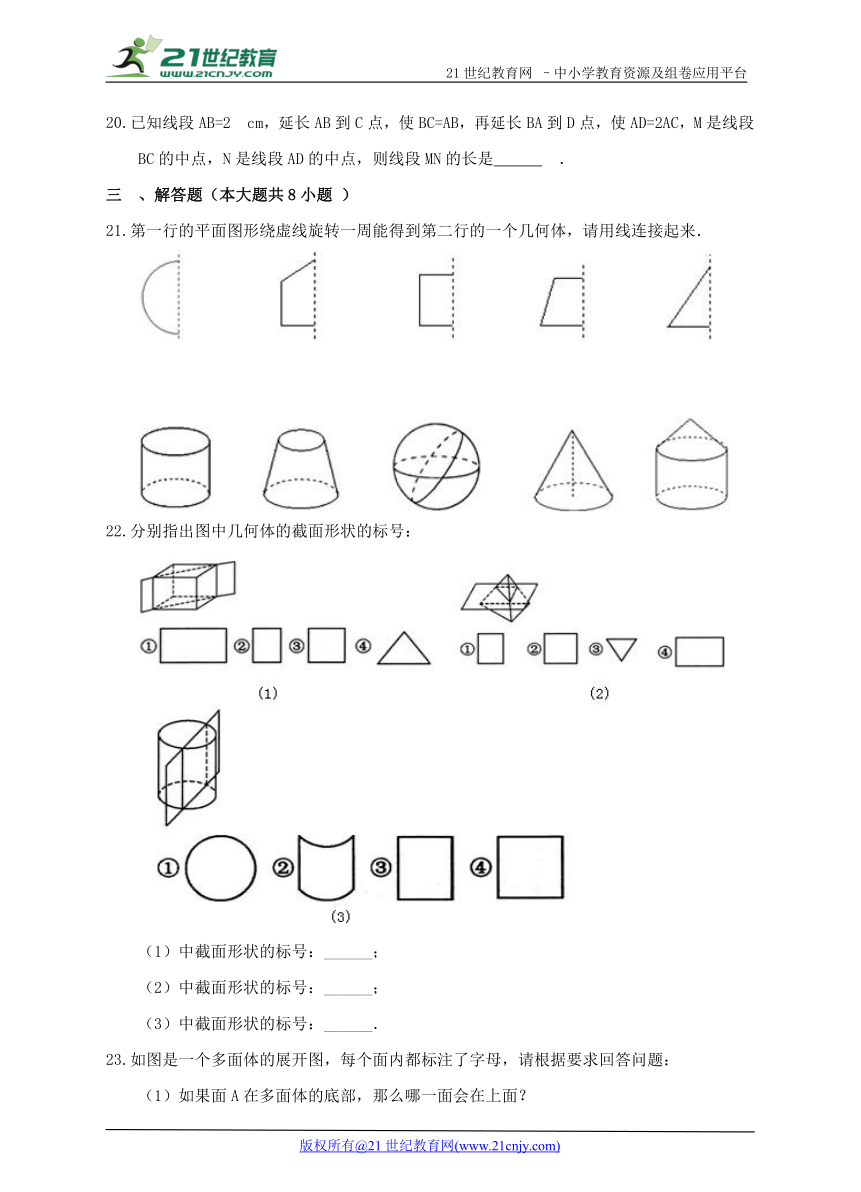
分别指出图中几何体的截面形状的标号:
(1)中截面形状的标号:______;
(2)中截面形状的标号:______;
(3)中截面形状的标号:______.
如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
(1)图中共有几条线段,分别表示出这些线段;
(2)若CB等于4cm,AB等于10cm,且D是AC的中点,求AD的长.
某人从A点出发向北偏东60°方向到B点,再从B点出发向南偏西15°,方向到C点,求∠ABC.
如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=21°,求∠ABC的度数.
如图,OC平分∠BOD,∠AOD=110°,∠COD=35°,求∠AOB的度数.
根据要求画图,并回答问题.
已知:直线AB、CD相交于点O,且OE⊥AB
(1)过点O画直线MN⊥CD;
(2)若点F是(1)所画直线MN上任意一点(O点除外),且∠AOC=34°,求∠EOF的度数.
答案解析
1 、选择题
【分析】利用圆规的特点直接得到答案即可.
解:圆规有两只脚,一铁脚固定,另一脚旋转,
故选D.
【分析】根据直线是向两方无限延伸的,射线是向一方无限延伸的,线段不能向任何一方无限延伸进行画图可得答案.
解:能相交的图形有①③.
故选:D.
【分析】 根据角平分线的定义对各选项进行逐一分析即可.
解:A.如图所示,
OC不是∠AOB的平分线,但是也符合∠AOC+∠BOC=∠AOB,故本选项错误;
B、当∠AOC=∠AOB时,OC是∠AOB的平分线,故本选项正确;
C、当∠AOC=∠AOB,∠BOC=∠AOB,∠AOB=2∠BOC时,OC是∠AOB的平分线,故本选项正确;
D、当∠AOC=∠BOC时,OC是∠AOB的平分线,故本选项正确.
故选A.
【分析】如图,点O是AB中点,连接DO,易知点D在量角器上对应的度数=∠DOB=2∠BCD,只要求出∠BCD的度数即可解决问题.
解:如图,点O是AB中点,连接DO.
∵点D在量角器上对应的度数=∠DOB=2∠BCD,
∵当射线CD将△ABC分割出以BC为边的等腰三角形时,
∠BCD=40°或70°,
∴点D在量角器上对应的度数=∠DOB=2∠BCD=80°或140°,
故选D.
【分析】直接利用两点之间的距离定义结合线段中点的性质分别分析得出答案.
解:A.当BM=AB时,则M为AB的中点,故此选项错误;
B、AM+BM=AB时,无法确定M为AB的中点,符合题意;
C、当AM=BM时,则M为AB的中点,故此选项错误;
D、当AB=2AM时,则M为AB的中点,故此选项错误;
故选:B.
【分析】利用钟表表盘的特征解答.表盘共被分成60小格,每一小格所对角的度数为6°.
解:分针经过24分钟,那么它转过的角度是:6°×24=144°.
故选B.
【分析】 本题没有给出图形,在画图时,应考虑到A.B、C三点之间的位置关系,再根据正确画出的图形解题.
解:
从图中我们可以发现AC+BC=AB,
所以点C在线段AB上.
故选A.
【分析】根据方位角的概念,画出方位角,利用平行线的性质,即可求解.
解:如图所示,
∵AD∥BE,∠1=50°,
∴∠ABE=∠DAB=50°,
∴∠ABC=50°-20°=30°.
故选B.
【分析】根据射线的表示,线段的性质,两点间的距离以及直线的性质对各小题分析判断即可得解.
解:①射线AB的端点是A,射线BA的端点是B,不是同一条射线,故本小题错误;
②两点之间的所有连线中,线段最短,正确;
③连接两点的线段的长度叫做这两点的距离,故本小题错误;
④欲将一根木条固定在墙上,至少需要2个钉子,正确;
综上所述,语句正确的有②④共2个.
故选B.
【分析】 首先根据余角与补角的定义,即可作出判断.
解:∵锐角的补角一定是钝角,∴①正确;
∵如90°角的补角的度数是90°,∴说一个角的补角一定大于这个角错误,∴②错误;
∵如果两个角是同一个角的补角,那么它们相等,∴③正确;
∵如∠A=10°,∠B=100°,当两角不互补,∴说锐角和钝角互补错误,∴④错误;
即正确的有2个,
故选B.
【分析】根据正方体展开图的类型,1﹣4﹣1型,2﹣3﹣1型,2﹣2﹣2型,3﹣3型,只有C不属于其中的类型,不能折成正方体,据此解答即可.
解:选项A,B,D折叠后都可以围成一个正方体,只有C折叠后第一行两个面无法折起来,而且下边没有面,不能折成正方体.
故选C.
【分析】连接BC,AC,BD,AD,AE,BE,再比较∠ACB,∠ADB,∠AEB的大小即可.
解:连接BC,AC,BD,AD,AE,BE,
通过测量可知∠ACB<∠ADB<∠AEB,所以射门的点越靠近线段DE,角越大,故最好选择DE(异于端点) 上一点,
故选C.
1 、填空题
【分析】根据直线的确定方法,易得答案.
解:根据两点确定一条直线.
故答案为:两点确定一条直线.
【分析】根据平行线性质得出∠1=∠A,代入求出即可.
解:
∵AE∥BF,
∴∠1=∠A=70°,
即在B点应按南偏西70°方向开凿,才能使铁路在山腹中准确接通,
故答案为:南偏西70°.
【分析】长方体的截面,最多可以经过6个面,所以边数最多的截面是六边形.
解:长方体的截面中,边数最多的多边形是六边形,即多边形的边数最多有6条.
【分析】根据余角、补角的定义计算.
解:∠A的余角的度数是90°﹣51°23′=38°37′.
故填38°37′.
【分析】根据点动成线可得答案.
解:“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明点动成线.
故答案为:点动成线.
【分析】根据已知条件“∠DOE=∠BOE,OF平分∠AOD,若∠BOE=28°”和平角的定义可以求得∠AOF=∠DOF=∠AOD=62°,∠DOE=∠BOE=28°;然后根据图形求得∠EOF=∠DOF+∠DOE=62°+28°=90°.
解:∵∠DOE=∠BOE,∠BOE=28°,
∴∠DOB=2∠BOE=56°;
又∵∠AOD+∠BOD=180°,
∴∠AOD=124°;
∵OF平分∠AOD,
∴∠AOF=∠DOF=∠AOD=62°,
∴∠EOF=∠DOF+∠DOE=62°+28°=90°.
故答案是:90°.
【分析】先根据题意找出各点的位置,然后直接计算即可.
解:画出图形如下所示:
则DC=DB+BC=AB+BC=1+4=5cm.
故答案为:5cm.
【分析】因为AB=BC,所以BC=2cm,AC=AB+BC=4,AD=2AC,所以AD=8cm,点N为AD中点,所以AN为4cm,点M是线段BC中点,所以BM为1cm,MN=NA+AB+BM,由此即可求出MN的长度.
解:∵AB=BC,AB=2 cm∴BC=2cm,AC=AB+BC=4
∵AD=2AC∴AD=8cm
∵点N为AD中点∴AN=4cm
∵点M是线段BC中点∴BM=1cm
∴MN=NA+AB+BM=4+2+1=7cm.
1 、解答题
【分析】根据面动成体结合常见立体图形的形状连接即可.
解:连接如图.
【分析】(1)根据图形可得沿对角线截取,进而得出所得形状;
(2)根据图形可得沿底面截取,进而得出所得形状;
(3)根据沿圆柱垂直平面截取,进而得出答案.
解:(1)中截面形状的标号:①;
(2)中截面形状的标号:③;
(3)中截面形状的标号:③.
故答案为:①,③,③.
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
解:这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
(1)面F会在上面;
(2)面C会在上面;
(3)面A会在上面.
【分析】(1)根据数线段的规律从一边数出即可;
(2)求出AC的长度,再根据线段中点的定义得出AD=AC,代入求出即可.
解:(1)有6条线段:AD,AC,AB,DC,DB,CB.
(2)∵CB=4cm,AB=10cm,
∴AC=AB-CB=10cm-4cm=6cm,
∵D是AC的中点,
∴AD=AC=×6cm=3cm.
【分析】根据方向角的定义首先作出示意图,然后求解即可.
解:作图如下
∵∠ABD=60°,∠CBD=15°,
∴∠ABC=∠ABD-∠CBD=60°-15°=45°.
【分析】由角平分线的定义,则∠CBD=∠DBA,根据BE分∠ABC分2:5两部分这一关系列出方程求解.
解:设∠ABE=2x°,
得2x+21=5x﹣21,
解得x=14,
∴∠ABC=14°×7=98°.
∴∠ABC的度数是98°.
故答案为98°.
【分析】 由角平分线的定义,结合角的运算,易求∠AOB的度数.
解:∵OC平分∠BOD,∠COD=35°,
∴∠BOD=2∠COD=70°,
又∵∠AOD=110°,
∴∠AOB=∠AOD﹣∠BOD=40°.
故答案为:40°.
【分析】(1)根据题意画出直线MN即可;
(2)当F在OM上时,根据垂直定义求出∠EOF=∠BOD,根据对顶角求出∠EOF=∠AOC,即可求出答案;当F在ON上时,求出∠AOM的度数,根据对顶角求出∠BON的度数,求出∠EOB+∠BON即可.
解:(1)如图.
(2)如上图:①当F在OM上时,
∵EO⊥AB,MN⊥CD,
∴∠EOB=∠MOD=90°,
∴∠MOE+∠EOD=90°,∠EOD+∠BOD=90°,
∴∠EOF=∠BOD=∠AOC=34°;
②当F在ON上时,如图在F′点时,
∵MN⊥CD,
∴∠MOC=90°=∠AOC+∠AOM,
∴∠AOM=90°﹣∠AOC=56°,
∴∠BON=∠AOM=56°,
∴∠EOF′=∠EOB+∠BON=90°+56°=146°,
答:∠EOF的度数是34°或146°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
图形的认识单元检测A卷
姓名:__________班级:__________学号:__________
1 、选择题(本大题共12小题 )
谜语:干活两腿脚,一腿勤,一腿懒,一脚站,一脚转.打一数学学习用具,谜底为( )
A.量角器 B.直尺 C.三角板 D.圆规
如图给出的分别有射线、直线、线段,其中能相交的图形有( )
A. ①②③④ B. ① C. ②③④ D. ①③
OC是∠AOB内的一条射线,下列所给的条件中,不能判断OC是∠AOB的平分线的是( )
A.∠AOC+∠BOC=∠AOB B.∠AOC=∠AOB
C.∠AOB=2∠AOC D.∠AOC=∠BOC
如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是( )
A.40° B.70° C.70°或80° D.80°或140°
如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
A.BM=AB B.AM+BM=AB C.AM=BM D.AB=2AM
钟表上的分针经过24分钟,分针转过的角度是( )
A.120゜ B.144゜ C.150゜ D.90゜
平面上有三点A,B,C,如果AB=8,AC=5,BC=3,下列说法正确的是( )
A.点C在线段AB上 B.点C在线段AB的延长线上
C.点C在直线AB外 D.点C可能在直线AB上,也可能在直线AB外
张雷同学从A地出发沿北偏东50°的方向行驶到B地,再由B地沿南偏西20°的方向行驶到C地,则∠ABC的度数为( )
A.40° B.30° C.20° D.10°
下列语句正确的有( )
①射线AB与射线BA是同一条射线
②两点之间的所有连线中,线段最短
③连接两点的线段叫做这两点的距离
④欲将一根木条固定在墙上,至少需要2个钉子.
A.1个 B.2个 C.3个 D.4个
下列说法中正确的个数是( )
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的补角,那么它们相等;④锐角和钝角互补.
A. 1 B. 2 C. 3 D. 4
如图不能折叠成正方体的是( )
A. B. C. D.
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A.点C B.点D或点E
C.线段DE(异于端点) 上一点 D.线段CD(异于端点) 上一点
1 、填空题(本大题共8小题 )
开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为______.
如图,A.B之间是一座山,一条铁路要通过A.B两地,在A地测得B地在北偏东70°,如果A.B两地同时开工修建铁路,那么在B地应按______方向开凿,才能使铁路在山腹中准确接通.
如图,用一个平面去截一个长方体,截面是一个多边形,这个多边形的边数最多有____条.
已知∠A=51°23′,则∠A的余角的度数是__________________.
在朱自清的《春》中有描写春雨“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明 .
如图,直线AB、CD相交于点O,∠DOE=∠BOE,OF平分∠AOD,若∠BOE=28°,则∠EOF的度数为______ .
已知线段AB=2cm,延长AB到点C,使BC=4cm,D为AB的中点,则线段DC=____________.
已知线段AB=2 cm,延长AB到C点,使BC=AB,再延长BA到D点,使AD=2AC,M是线段BC的中点,N是线段AD的中点,则线段MN的长是 .
1 、解答题(本大题共8小题 )
第一行的平面图形绕虚线旋转一周能得到第二行的一个几何体,请用线连接起来.
分别指出图中几何体的截面形状的标号:
(1)中截面形状的标号:______;
(2)中截面形状的标号:______;
(3)中截面形状的标号:______.
如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
(1)图中共有几条线段,分别表示出这些线段;
(2)若CB等于4cm,AB等于10cm,且D是AC的中点,求AD的长.
某人从A点出发向北偏东60°方向到B点,再从B点出发向南偏西15°,方向到C点,求∠ABC.
如图,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=21°,求∠ABC的度数.
如图,OC平分∠BOD,∠AOD=110°,∠COD=35°,求∠AOB的度数.
根据要求画图,并回答问题.
已知:直线AB、CD相交于点O,且OE⊥AB
(1)过点O画直线MN⊥CD;
(2)若点F是(1)所画直线MN上任意一点(O点除外),且∠AOC=34°,求∠EOF的度数.
答案解析
1 、选择题
【分析】利用圆规的特点直接得到答案即可.
解:圆规有两只脚,一铁脚固定,另一脚旋转,
故选D.
【分析】根据直线是向两方无限延伸的,射线是向一方无限延伸的,线段不能向任何一方无限延伸进行画图可得答案.
解:能相交的图形有①③.
故选:D.
【分析】 根据角平分线的定义对各选项进行逐一分析即可.
解:A.如图所示,
OC不是∠AOB的平分线,但是也符合∠AOC+∠BOC=∠AOB,故本选项错误;
B、当∠AOC=∠AOB时,OC是∠AOB的平分线,故本选项正确;
C、当∠AOC=∠AOB,∠BOC=∠AOB,∠AOB=2∠BOC时,OC是∠AOB的平分线,故本选项正确;
D、当∠AOC=∠BOC时,OC是∠AOB的平分线,故本选项正确.
故选A.
【分析】如图,点O是AB中点,连接DO,易知点D在量角器上对应的度数=∠DOB=2∠BCD,只要求出∠BCD的度数即可解决问题.
解:如图,点O是AB中点,连接DO.
∵点D在量角器上对应的度数=∠DOB=2∠BCD,
∵当射线CD将△ABC分割出以BC为边的等腰三角形时,
∠BCD=40°或70°,
∴点D在量角器上对应的度数=∠DOB=2∠BCD=80°或140°,
故选D.
【分析】直接利用两点之间的距离定义结合线段中点的性质分别分析得出答案.
解:A.当BM=AB时,则M为AB的中点,故此选项错误;
B、AM+BM=AB时,无法确定M为AB的中点,符合题意;
C、当AM=BM时,则M为AB的中点,故此选项错误;
D、当AB=2AM时,则M为AB的中点,故此选项错误;
故选:B.
【分析】利用钟表表盘的特征解答.表盘共被分成60小格,每一小格所对角的度数为6°.
解:分针经过24分钟,那么它转过的角度是:6°×24=144°.
故选B.
【分析】 本题没有给出图形,在画图时,应考虑到A.B、C三点之间的位置关系,再根据正确画出的图形解题.
解:
从图中我们可以发现AC+BC=AB,
所以点C在线段AB上.
故选A.
【分析】根据方位角的概念,画出方位角,利用平行线的性质,即可求解.
解:如图所示,
∵AD∥BE,∠1=50°,
∴∠ABE=∠DAB=50°,
∴∠ABC=50°-20°=30°.
故选B.
【分析】根据射线的表示,线段的性质,两点间的距离以及直线的性质对各小题分析判断即可得解.
解:①射线AB的端点是A,射线BA的端点是B,不是同一条射线,故本小题错误;
②两点之间的所有连线中,线段最短,正确;
③连接两点的线段的长度叫做这两点的距离,故本小题错误;
④欲将一根木条固定在墙上,至少需要2个钉子,正确;
综上所述,语句正确的有②④共2个.
故选B.
【分析】 首先根据余角与补角的定义,即可作出判断.
解:∵锐角的补角一定是钝角,∴①正确;
∵如90°角的补角的度数是90°,∴说一个角的补角一定大于这个角错误,∴②错误;
∵如果两个角是同一个角的补角,那么它们相等,∴③正确;
∵如∠A=10°,∠B=100°,当两角不互补,∴说锐角和钝角互补错误,∴④错误;
即正确的有2个,
故选B.
【分析】根据正方体展开图的类型,1﹣4﹣1型,2﹣3﹣1型,2﹣2﹣2型,3﹣3型,只有C不属于其中的类型,不能折成正方体,据此解答即可.
解:选项A,B,D折叠后都可以围成一个正方体,只有C折叠后第一行两个面无法折起来,而且下边没有面,不能折成正方体.
故选C.
【分析】连接BC,AC,BD,AD,AE,BE,再比较∠ACB,∠ADB,∠AEB的大小即可.
解:连接BC,AC,BD,AD,AE,BE,
通过测量可知∠ACB<∠ADB<∠AEB,所以射门的点越靠近线段DE,角越大,故最好选择DE(异于端点) 上一点,
故选C.
1 、填空题
【分析】根据直线的确定方法,易得答案.
解:根据两点确定一条直线.
故答案为:两点确定一条直线.
【分析】根据平行线性质得出∠1=∠A,代入求出即可.
解:
∵AE∥BF,
∴∠1=∠A=70°,
即在B点应按南偏西70°方向开凿,才能使铁路在山腹中准确接通,
故答案为:南偏西70°.
【分析】长方体的截面,最多可以经过6个面,所以边数最多的截面是六边形.
解:长方体的截面中,边数最多的多边形是六边形,即多边形的边数最多有6条.
【分析】根据余角、补角的定义计算.
解:∠A的余角的度数是90°﹣51°23′=38°37′.
故填38°37′.
【分析】根据点动成线可得答案.
解:“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明点动成线.
故答案为:点动成线.
【分析】根据已知条件“∠DOE=∠BOE,OF平分∠AOD,若∠BOE=28°”和平角的定义可以求得∠AOF=∠DOF=∠AOD=62°,∠DOE=∠BOE=28°;然后根据图形求得∠EOF=∠DOF+∠DOE=62°+28°=90°.
解:∵∠DOE=∠BOE,∠BOE=28°,
∴∠DOB=2∠BOE=56°;
又∵∠AOD+∠BOD=180°,
∴∠AOD=124°;
∵OF平分∠AOD,
∴∠AOF=∠DOF=∠AOD=62°,
∴∠EOF=∠DOF+∠DOE=62°+28°=90°.
故答案是:90°.
【分析】先根据题意找出各点的位置,然后直接计算即可.
解:画出图形如下所示:
则DC=DB+BC=AB+BC=1+4=5cm.
故答案为:5cm.
【分析】因为AB=BC,所以BC=2cm,AC=AB+BC=4,AD=2AC,所以AD=8cm,点N为AD中点,所以AN为4cm,点M是线段BC中点,所以BM为1cm,MN=NA+AB+BM,由此即可求出MN的长度.
解:∵AB=BC,AB=2 cm∴BC=2cm,AC=AB+BC=4
∵AD=2AC∴AD=8cm
∵点N为AD中点∴AN=4cm
∵点M是线段BC中点∴BM=1cm
∴MN=NA+AB+BM=4+2+1=7cm.
1 、解答题
【分析】根据面动成体结合常见立体图形的形状连接即可.
解:连接如图.
【分析】(1)根据图形可得沿对角线截取,进而得出所得形状;
(2)根据图形可得沿底面截取,进而得出所得形状;
(3)根据沿圆柱垂直平面截取,进而得出答案.
解:(1)中截面形状的标号:①;
(2)中截面形状的标号:③;
(3)中截面形状的标号:③.
故答案为:①,③,③.
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
解:这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
(1)面F会在上面;
(2)面C会在上面;
(3)面A会在上面.
【分析】(1)根据数线段的规律从一边数出即可;
(2)求出AC的长度,再根据线段中点的定义得出AD=AC,代入求出即可.
解:(1)有6条线段:AD,AC,AB,DC,DB,CB.
(2)∵CB=4cm,AB=10cm,
∴AC=AB-CB=10cm-4cm=6cm,
∵D是AC的中点,
∴AD=AC=×6cm=3cm.
【分析】根据方向角的定义首先作出示意图,然后求解即可.
解:作图如下
∵∠ABD=60°,∠CBD=15°,
∴∠ABC=∠ABD-∠CBD=60°-15°=45°.
【分析】由角平分线的定义,则∠CBD=∠DBA,根据BE分∠ABC分2:5两部分这一关系列出方程求解.
解:设∠ABE=2x°,
得2x+21=5x﹣21,
解得x=14,
∴∠ABC=14°×7=98°.
∴∠ABC的度数是98°.
故答案为98°.
【分析】 由角平分线的定义,结合角的运算,易求∠AOB的度数.
解:∵OC平分∠BOD,∠COD=35°,
∴∠BOD=2∠COD=70°,
又∵∠AOD=110°,
∴∠AOB=∠AOD﹣∠BOD=40°.
故答案为:40°.
【分析】(1)根据题意画出直线MN即可;
(2)当F在OM上时,根据垂直定义求出∠EOF=∠BOD,根据对顶角求出∠EOF=∠AOC,即可求出答案;当F在ON上时,求出∠AOM的度数,根据对顶角求出∠BON的度数,求出∠EOB+∠BON即可.
解:(1)如图.
(2)如上图:①当F在OM上时,
∵EO⊥AB,MN⊥CD,
∴∠EOB=∠MOD=90°,
∴∠MOE+∠EOD=90°,∠EOD+∠BOD=90°,
∴∠EOF=∠BOD=∠AOC=34°;
②当F在ON上时,如图在F′点时,
∵MN⊥CD,
∴∠MOC=90°=∠AOC+∠AOM,
∴∠AOM=90°﹣∠AOC=56°,
∴∠BON=∠AOM=56°,
∴∠EOF′=∠EOB+∠BON=90°+56°=146°,
答:∠EOF的度数是34°或146°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
