人教版八年级上册数学第11章11.1.1《三角形的边》课件
文档属性
| 名称 | 人教版八年级上册数学第11章11.1.1《三角形的边》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-15 00:00:00 | ||
图片预览




文档简介
课件17张PPT。第十一章
三角形的边 学习目标 1、了解三角形的基本概念;
2、理解三角形三边长的关系;
3、能结合具体的题目讨论三角形的三边关系.阅读教材P2-4 ,回答下列问题:1、什么是三角形,三角形的顶点、角、边?
2、三角形可以怎么分类?
3、三角形中三边满足什么关系?
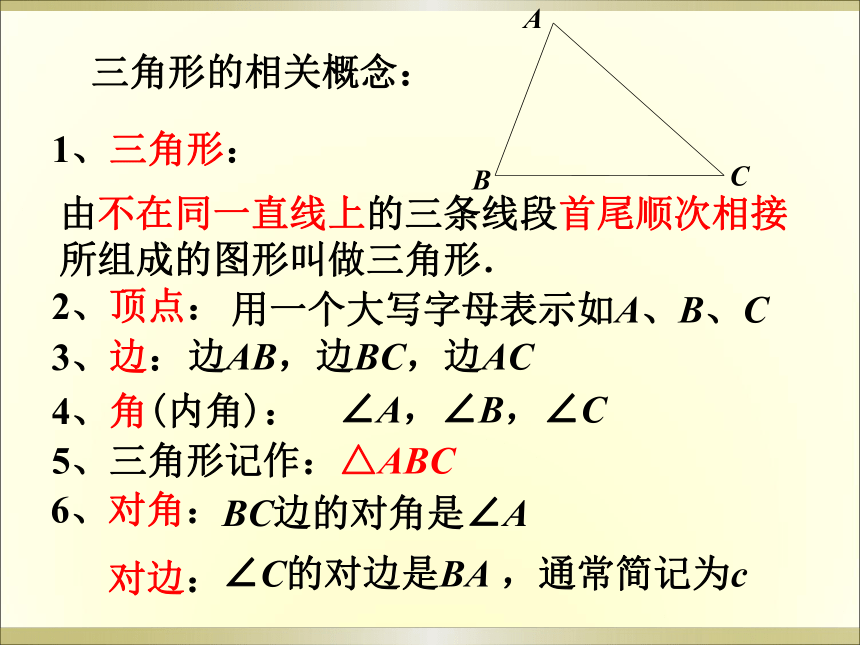
4、已知三角形的两边,则第三边有什么范围要求?1、三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、顶点: 用一个大写字母表示如A、B、C 3、边: 边AB,边BC,边AC
4、角(内角): ∠A,∠B,∠C 5、三角形记作:△ABCABC6、对角:
对边: 三角形的相关概念:∠C的对边是BA ,通常简记为cBC边的对角是∠A三角形分类按边的相等关系不等边三角形等腰三角形底边和腰不相等的
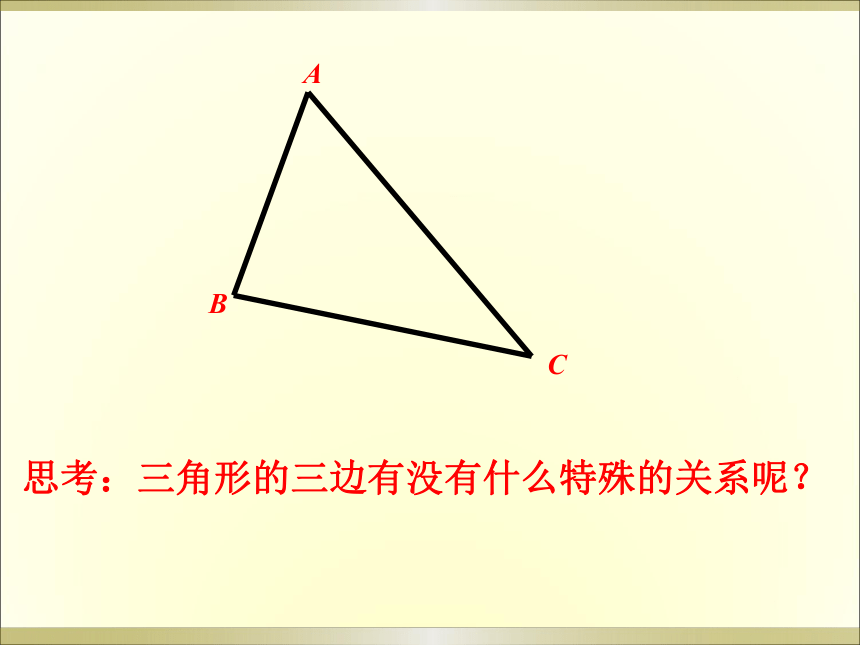
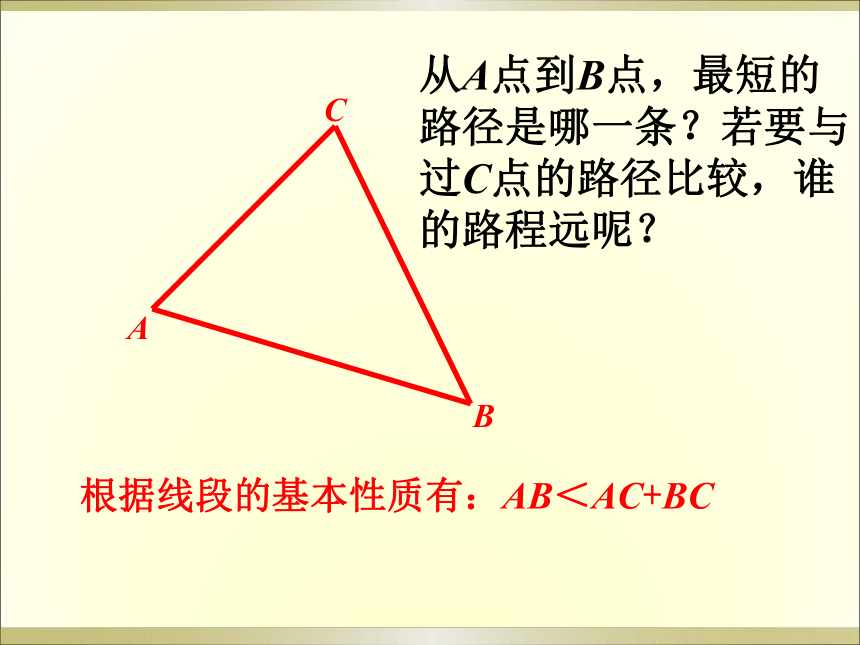
等腰三角形等边三角形思考:三角形的三边有没有什么特殊的关系呢?A BC 从A点到B点,最短的路径是哪一条?若要与过C点的路径比较,谁的路程远呢? 根据线段的基本性质有:AB<AC+BC那么在任意一个三角形当中,任意两边之和与第三边的长度有怎样的关系?为什么?定理:三角形任何两边之和大于第三边.即:在任意△ABC中有
a+b>c 、 b+c>a 、 a + c > b 给出一个任意三角形,利用工具测量出这个三角形三边的长度.计算测得三角形的任意两边之差,并与第三边比较,你能得到什么结论?推论:三角形任何两边的差小于第三边试一试1、下列长度的三条线段能否组成三角形?为什么?(1)3 , 4, 8 (2)5 , 6 , 11 (3)5 ,6,10解:(1)不能组成三角形,因为3+4<8,即两条线段的和
小于第三条线段,所以不能组成三角形.(2)不能组成三角形,因为5+6=11即两条线段的和等于第三条直线,所以不能组成三角形.(3)能组成三角形,因为任意两条线段的和都大于第三条线段.若两条较短边的和大于最长边,
则可构成三角形,否则不能.快速口答2、下列长度的各组线段能否组成一个三角形?
(1)15cm、9cm、7cm; (2)3cm、6cm、10cm
(3)3cm、8cm、5cm; (4)2cm、5cm、6cm解: (1) ∵ 9+7>15, ∴能组成三角形;
(2) ∵ 3+6<10, ∴不能组成三角形;
(3) ∵ 3+5=8, ∴不能组成三角形;
(4) ∵ 2+5>6, ∴能组成三角形. 1、判断三条已知线段能否组成三角形: 小结:
若两条较短边的和大于最长边,
则可构成三角形,否则不能. 两边之差<第三边<两边之和 2、确定三角形第三边的取值范围:例 用一根长为18厘米的细铁丝围成一个 等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4厘米的等腰三角形吗?为什么?解:设底边长为x厘米,则腰长为2x厘米
x+2x+2x=18
解得:x=3.6
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
因为4+4<10,出现两边和小于第三边的情况,所以不能围成腰长为4厘米的等腰三角形.
由以上结论可知,可以围成底边长是4厘米的等腰三角形.解:因为长为4厘米的边可能是腰,也可能是底边,所以需要分情况讨论.(1)如果4厘米长为底边,设腰长为x厘米则
4+2x=18解得x=7.(2)如果4厘米长为腰,设底边长为X厘米,则2×4+x=18,解得x=10.小结:请谈一谈,这节课你学到了什么?
课后作业教材第8页的第1、2题
2、理解三角形三边长的关系;
3、能结合具体的题目讨论三角形的三边关系.阅读教材P2-4 ,回答下列问题:1、什么是三角形,三角形的顶点、角、边?
2、三角形可以怎么分类?
3、三角形中三边满足什么关系?
4、已知三角形的两边,则第三边有什么范围要求?1、三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、顶点: 用一个大写字母表示如A、B、C 3、边: 边AB,边BC,边AC
4、角(内角): ∠A,∠B,∠C 5、三角形记作:△ABCABC6、对角:
对边: 三角形的相关概念:∠C的对边是BA ,通常简记为cBC边的对角是∠A三角形分类按边的相等关系不等边三角形等腰三角形底边和腰不相等的
等腰三角形等边三角形思考:三角形的三边有没有什么特殊的关系呢?A BC 从A点到B点,最短的路径是哪一条?若要与过C点的路径比较,谁的路程远呢? 根据线段的基本性质有:AB<AC+BC那么在任意一个三角形当中,任意两边之和与第三边的长度有怎样的关系?为什么?定理:三角形任何两边之和大于第三边.即:在任意△ABC中有
a+b>c 、 b+c>a 、 a + c > b 给出一个任意三角形,利用工具测量出这个三角形三边的长度.计算测得三角形的任意两边之差,并与第三边比较,你能得到什么结论?推论:三角形任何两边的差小于第三边试一试1、下列长度的三条线段能否组成三角形?为什么?(1)3 , 4, 8 (2)5 , 6 , 11 (3)5 ,6,10解:(1)不能组成三角形,因为3+4<8,即两条线段的和
小于第三条线段,所以不能组成三角形.(2)不能组成三角形,因为5+6=11即两条线段的和等于第三条直线,所以不能组成三角形.(3)能组成三角形,因为任意两条线段的和都大于第三条线段.若两条较短边的和大于最长边,
则可构成三角形,否则不能.快速口答2、下列长度的各组线段能否组成一个三角形?
(1)15cm、9cm、7cm; (2)3cm、6cm、10cm
(3)3cm、8cm、5cm; (4)2cm、5cm、6cm解: (1) ∵ 9+7>15, ∴能组成三角形;
(2) ∵ 3+6<10, ∴不能组成三角形;
(3) ∵ 3+5=8, ∴不能组成三角形;
(4) ∵ 2+5>6, ∴能组成三角形. 1、判断三条已知线段能否组成三角形: 小结:
若两条较短边的和大于最长边,
则可构成三角形,否则不能. 两边之差<第三边<两边之和 2、确定三角形第三边的取值范围:例 用一根长为18厘米的细铁丝围成一个 等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4厘米的等腰三角形吗?为什么?解:设底边长为x厘米,则腰长为2x厘米
x+2x+2x=18
解得:x=3.6
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
因为4+4<10,出现两边和小于第三边的情况,所以不能围成腰长为4厘米的等腰三角形.
由以上结论可知,可以围成底边长是4厘米的等腰三角形.解:因为长为4厘米的边可能是腰,也可能是底边,所以需要分情况讨论.(1)如果4厘米长为底边,设腰长为x厘米则
4+2x=18解得x=7.(2)如果4厘米长为腰,设底边长为X厘米,则2×4+x=18,解得x=10.小结:请谈一谈,这节课你学到了什么?
课后作业教材第8页的第1、2题
