第4章 图形的认识单元检测B卷
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
21世纪教育网 –中小学教育资源及组卷应用平台
图形的认识单元检测B卷
姓名:__________班级:__________学号:__________
、选择题(本大题共12小题,每小题4分,共48分 )
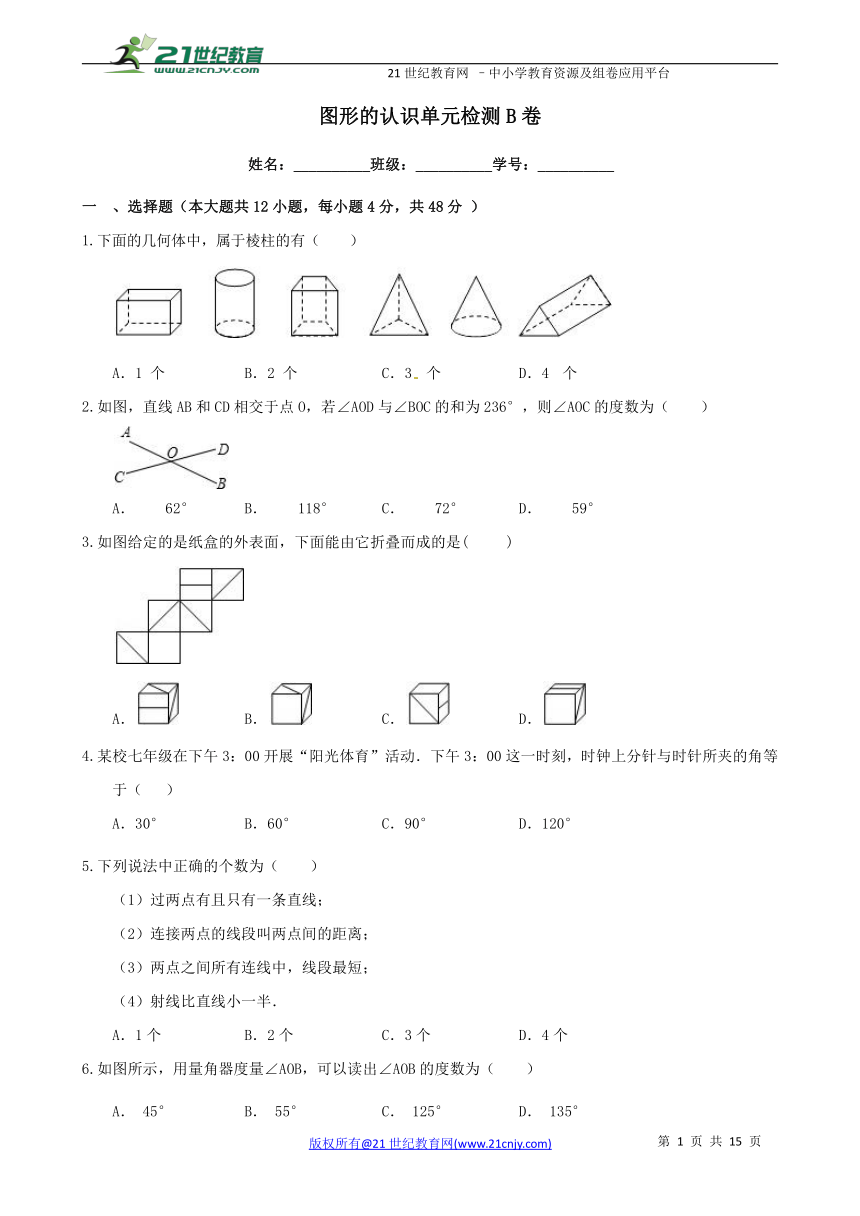
下面的几何体中,属于棱柱的有( )
A.1 个 B.2 个 C.3 个 D.4 个
如图,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A. 62° B. 118° C. 72° D. 59°
如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
A. B. C. D.
某校七年级在下午3:00开展“阳光体育”活动.下午3:00这一时刻,时钟上分针与时针所夹的角等于( )
A.30° B.60° C.90° D.120°
下列说法中正确的个数为( )
(1)过两点有且只有一条直线;
(2)连接两点的线段叫两点间的距离;
(3)两点之间所有连线中,线段最短;
(4)射线比直线小一半.
A.1个 B.2个 C.3个 D.4个
如图所示,用量角器度量∠AOB,可以读出∠AOB的度数为( )
A. 45° B. 55° C. 125° D. 135°
下列结论中,不正确的是( )
A.两点确定一条直线 B.两点之间,直线最短
C.等角的余角相等 D.等角的补角相等
平面上有三个点,可以确定直线的条数是 ( )
A.1条 B.2条 C.3条 D.1条或3条
某公司员工分别在A.B、C三个住宅区,A区有30人,B区有30人,C区有10人,三个区在同一条直线上,如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
A.A区 B.B区 C.C区 D.A.B两区之间
已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC等于( )
A.120° B.120°或60° C.30° D.30°或90°
已知线段AB=6cm,若M是AB的三等分点,N是AM的中点,则线段MN的长度为( )
A.1cm B.2cm C.1.5cm D.1cm或2cm
挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走。如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走( )
A.②号棒 B.⑦号棒 C.⑧号棒 D.⑩号棒
、填空题(本大题共6小题,每小题4分,共24分)
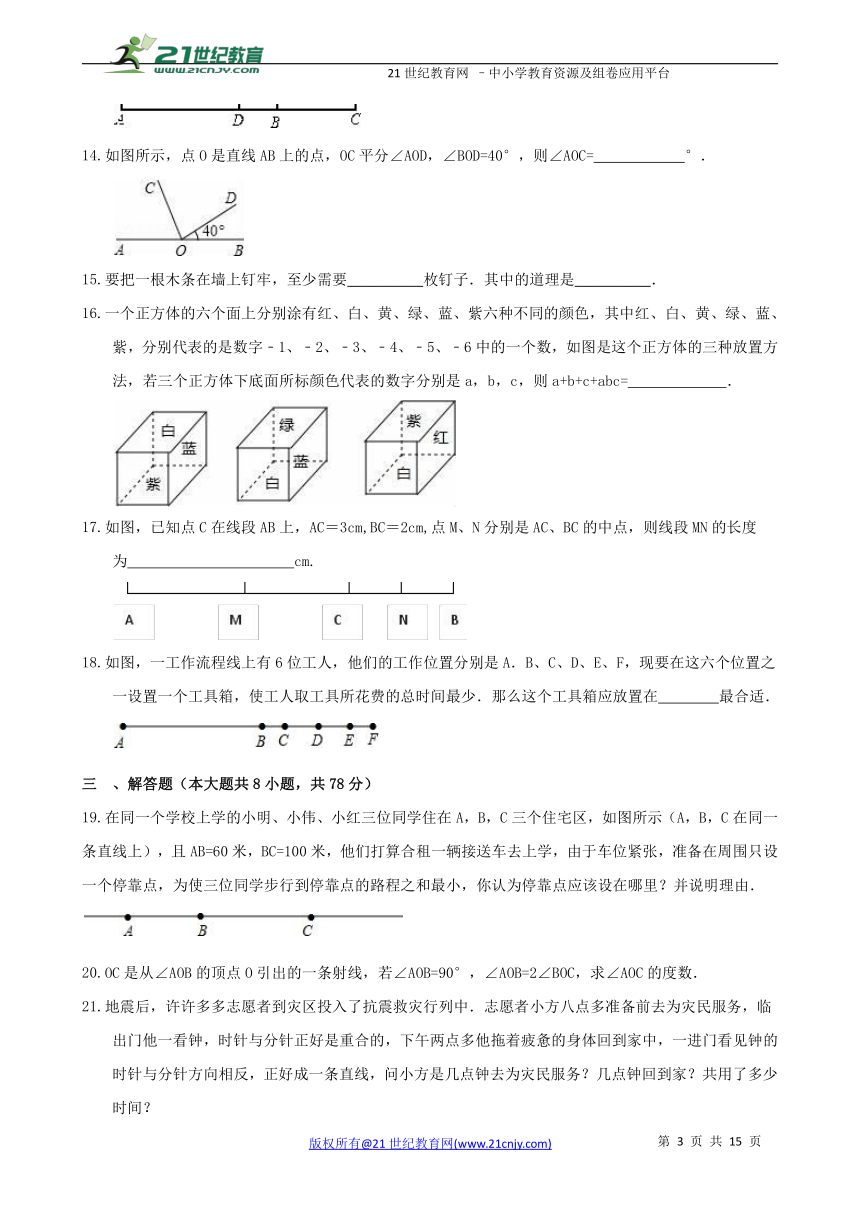
如图,已知线段AC,点D为AC的中点,BC=AB,BD=1cm,则AC=__________.
如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=40°,则∠AOC= °.
要把一根木条在墙上钉牢,至少需要__________枚钉子.其中的道理是__________.
一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字﹣1、﹣2、﹣3、﹣4、﹣5、﹣6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc= .
如图,已知点C在线段AB上,AC=3cm,BC=2cm,点M、N分别是AC、BC的中点,则线段MN的长度为 cm.
如图,一工作流程线上有6位工人,他们的工作位置分别是A.B、C、D、E、F,现要在这六个位置之一设置一个工具箱,使工人取工具所花费的总时间最少.那么这个工具箱应放置在 最合适.
、解答题(本大题共8小题,共78分)
在同一个学校上学的小明、小伟、小红三位同学住在A,B,C三个住宅区,如图所示(A,B,C在同一条直线上),且AB=60米,BC=100米,他们打算合租一辆接送车去上学,由于车位紧张,准备在周围只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在哪里?并说明理由.
OC是从∠AOB的顶点O引出的一条射线,若∠AOB=90°,∠AOB=2∠BOC,求∠AOC的度数.
地震后,许许多多志愿者到灾区投入了抗震救灾行列中.志愿者小方八点多准备前去为灾民服务,临出门他一看钟,时针与分针正好是重合的,下午两点多他拖着疲惫的身体回到家中,一进门看见钟的时针与分针方向相反,正好成一条直线,问小方是几点钟去为灾民服务?几点钟回到家?共用了多少时间?
在线段AB上顺次取三点C、D、E.
(1)若C、D、E是AB的四个等分点,画出图形,并求图中所有线段条数;
(2)若AB=12,求(1)中所有线段的长度;
(3)当C、D、E是线段上顺次三点时,若AB=12.CE=2,求图中所有线段的长度和.
如图,点C在线段AB上,线段AC=8cm,BC=4cm,点M、N分别是AC、BC的中点,求:
(1)线段MN的长度.
(2)根据(1)的计算过程和结果,设AC+BC=a,其它条件不变,你能猜测出MN的长度吗?请证明你的猜测.
如图,点C在AB上,点M、N分别是AC、BC的中点,
(1)若AC=12cm,BC=10cm,求线段MN的长;
(2)若点C为线段AB上任意一点,满足AC+BC=acm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若点C在线段AB的延长线上,且满足AC﹣BC=bcm,点M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.请用一句简洁的话描述你发现的结论.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上,作直线DE,DF平分∠BDE,DF与BC交于点F.
(1)依题意补全图形;
(2)当∠B+∠BDF=90°时,∠A与∠EDF是否相等?说明理由.
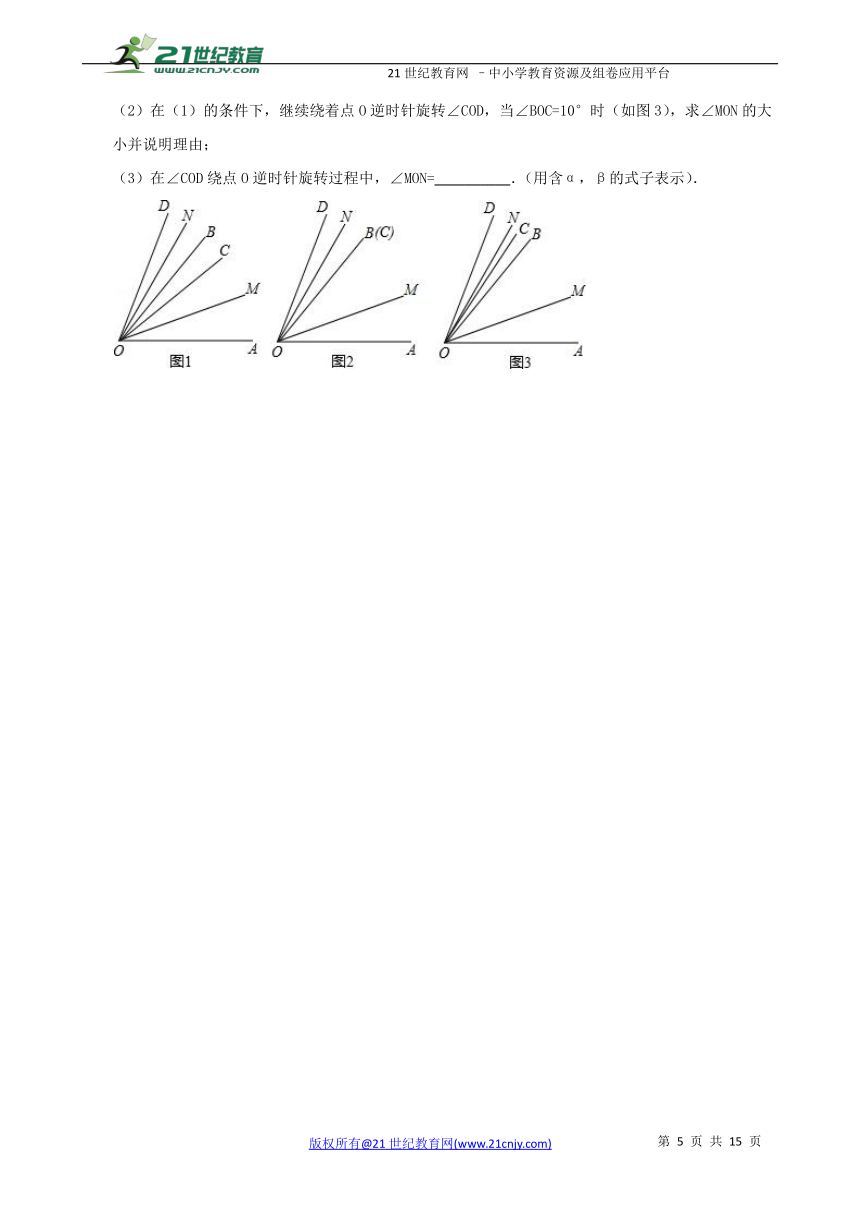
如图1,∠AOB=α,∠COD=β,OM,ON分别是∠AOC,∠BOD的角平分线.
(1)若∠AOB=50°,∠COD=30°,当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图2),则∠MON的大小为__________;
(2)在(1)的条件下,继续绕着点O逆时针旋转∠COD,当∠BOC=10°时(如图3),求∠MON的大小并说明理由;
(3)在∠COD绕点O逆时针旋转过程中,∠MON=__________.(用含α,β的式子表示).
答案解析
、选择题
解:从左到右依次是长方体,圆柱,棱柱,棱锥,圆锥,棱柱. 故选:C.
【分析】利用对顶角的定义以及周角定义得出∠AOC的度数.
解:∵直线AB和CD相交于点O,∠AOD与∠BOC的和为236°,
∴∠AOC=∠BOD==62°.
故选A.
【分析】将A.B、C、D分别展开,能和原图相对应的即为正确答案.
解:A.展开得到,不能和原图相对应,故本选项错误;
B、展开得到,能和原图相对,故本选项正确;
C、展开得到,不能和原图相对应,故本选项错误;
D、展开得到,不能和原图相对应,故本选项错误.
故选B.
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,借助图形,找出时针和分针之间相差的大格数,用大格数乘30°即可.
解:∵3点整,时针指向3,分针指向12.
钟表12个数字,每相邻两个数字之间的夹角为30°,
∴3点整分针与时针的夹角正好是30°×3=90°.
故选:C.
【分析】 根据直线、射线等相关的定义或定理分别判断得出答案即可.
解:(1)过两点有且只有一条直线,此选项正确;
(2)连接两点的线段的长度叫两点间的距离,此选项错误;
(3)两点之间所有连线中,线段最短,此选项正确;
(4)射线比直线小一半,根据射线与直线都无限长,故此选项错误;
故正确的有2个.
故选:B.
解:由生活知识可知这个角小于90度,排除C、D,又OB边在50与60之间,所以,度数应为55°。
故选:B.
【分析】 根据线段的性质:两点之间线段最短,可以确定“两点之间,直线最短”是错误的.
解:A.公理.
B、两点之间,线段最短.
C、等角的余角相等.
D、等角的补角相等.
故选B.
【分析】分别从若平面内的三个点A.B、C不在同一直线上与若平面内的三个点A.B、C在同一直线上去分析,则可求得答案.
解:∵若平面内的三个点A.B、C不在同一直线上,则能确定的直线的条数是:3条;
若平面内的三个点A.B、C在同一直线上,则能确定的直线的条数是:1条.
∴平面内的三个点A.B、C能确定的直线的条数是:1条或3条.
故选D.
【分析】分①设在A区、B区之间时,设距离A区x米,表示出所有员工的步行总路程之和,然后求出最小值,②设在B区、C区之间时,设距离B区x米,表示出所有员工的步行总路程之和,然后求出最小值,比较即可得解.
解:①设在A区、B区之间时,设距离A区x米,
则所有员工步行路程之和=30x+30(100-x)+10(100+200-x),
=30x+3000-30x+3000-10x,
=-10x+6000,
∴当x最大为100时,即在B区时,路程之和最小,为5000米;
②设在B区、C区之间时,设距离B区x米,
则所有员工步行路程之和=30(100+x)+30x+10(200-x),
=3000+30x+30x+2000-10x,
=50x+5000,
∴当x最大为0时,即在B区时,路程之和最小,为5000米;
综上所述,停靠点的位置应设在B区.
故选B.
【分析】 此题需要分类讨论,共两种情况.先作图后计算.
解:∵∠BOC=30°,∠AOB=3∠BOC,
∴∠AOB=3×30°=90°
(1)当OC在∠AOB的外侧时,
∠AOC=∠AOB+∠BOC=90°+30°=120度;
(2)当OC在∠AOB的内侧时,
∠AOC=∠AOB﹣∠BOC=90°﹣30°=60度.
故选:B.
【分析】根据M是AB的三等分点,可得AM的长,再根据线段中点的性质,可得答案.
解:由线段AB=6cm,若M是AB的三等分点,得
AM=2,或AM=4.
当AM=2cm时,由N是AM的中点,得MN=AM=×2=1(cm);
当AM=4cm时,由N是AM的中点,得MN=AM=×4=2(cm);
故选:D.
【分析】 本题考查动手实践操作能力和空间想象能力,体现了做数学的数学思想方法。按照条件中的游戏规则,第1次应拿走9号棒、第2次应拿走5号棒,第3次应拿走6号棒,第4次应拿走2号棒,第5次应拿走8号棒,第6次应拿走10号棒,第7次应拿走7号棒,第8次应拿走3号棒,第9次应拿走4号棒,第10次应拿走1号棒,
从图中看,可知从上到下的棒的序号依次是⑨⑤⑥②⑧⑩⑦③④①,因此第6次应拿走⑩号棒;
故选D
、填空题
【分析】根据线段中点的性质,可得DC=AC,根据BC=AB,可得BC与AC的关系,根据线段的和差,可得答案.
解:由点D为AC的中点,得
DC=AC.
由BC=AB,得
AB=2BC,AC=BC+AB=3BC,
BCAC,
由线段的和差,得
BD=CD﹣BC,即AC﹣AC=1,
解得AC=6cm,
故答案为:6cm.
【分析】根据∠AOD是∠BOD的补角求得∠AOD的度数,然后根据角平分线的定义求∠AOC的度数.
解:∵∠AOD+∠BOD=180°,∠BOD=40°,
∴∠AOD=140°;
∵OC平分∠AOD,
∴∠AOC=∠COD=∠AOD=70°;
故答案是:70.
【分析】根据两点确定一条直线解答.
解:把一根木条钉牢在墙上,至少需要两枚钉子,其中的道理是:两点确定一条直线.
故答案为:两,两点确定一条直线.
【分析】先根据图中正方形的摆放方式可知与白色面相邻的面有紫、蓝、绿、红,然后再确定出其中相对的面,从而得出a、b、c的值,最后代入计算即可.
解:∵根据图形可知:白色面相邻的面有紫、蓝、绿、红,
∴“紫”与“绿”是对面,“红”与“蓝”是对面,“白”与“黄”是对面.
∴第一个正方体的底面是黄色,第二个正方体的底面是紫色,第三个正方体的底面是绿色.
∴a=﹣3,b=﹣6,c=﹣4.
∴a+b+c+abc=(﹣3)+(﹣6)+(﹣4)+(﹣3)×(﹣6)×(﹣4)=﹣13+(﹣72)=﹣85.
故答案为:﹣85.
【分析】由已知条件可知,MN=MC+NC,又因为点M、N分别是AC、BC的中点,则MC=AC,NC=BC,故MN=MC+NC=(AC+BC)=AB.
解:∵AC=3cm,BC=2cm,
点M、N分别是AC、BC的中点,
∴MC=cm,NC=1cm,
∴MN=MC+NC=cm.
【分析】总时间最少就是总路程最短.因此可采用分类讨论的思想,假设工具箱分别设置在A.B、C、D、E、F的位置,根据图示求出设置在以上位置时工人经过的总路程,然后进行比较,总路程最短的即为正确答案.
解:如设在A点,总路程为:5AB+4BC+3CD+2DE+EF;
如设在B点,总路程为:AB+4BC+3CD+2DE+EF;
如设在C点,总路程为:AB+2BC+3CD+2DE+EF;
如设在D点,总路程为:AB+2BC+3CD+2DE+EF;
如设在E点,总路程为:AB+2BC+3CD+4DE+EF;
如设在F点,总路程为:AB+2BC+3CD+4DE+EF;
通过比较可以发现,如设在C点和D点总路程最短,所以花费的总时间最少.
故答案为:C或D的位置.
、解答题
【分析】根据小明、小红步行的距离之和为A.C两点间的距离不变,判断出小伟步行的距离最小时,三人的总路程之和最小解答.
解:停靠点设在B点时,三位同学步行到停靠点的路程之和最小,
是60+100=160米,
理由如下:小明、小红步行的距离之和为A.C两点间的距离不变,
小伟步行的距离是0米时,三位同学步行到停靠点的路程之和最小.
【分析】利用角的和差关系计算,注意此题要分两种情况.
解:①如图1所示,OC在∠AOB内部,
∵∠AOB=90°,∠AOB=2∠BOC,
∴∠BOC=×90°=45°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣45°=45°;
②如图2所示,OC在∠AOB外部,
∵∠AOB=90°,∠AOB=2∠BOC,
∴∠BOC=×90°=45°,
又∵∠AOC=∠AOB+∠BOC,
∴∠AOC=90°+45°=135°.
【分析】在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动()°依据这一关系列出方程,可以求出.
解:设8点x分时针与分针重合,
则:x-=40,
解得:x=43.
即8点43分时出门.
设2点y分时,时针与分针方向相反.
则:y-=10+30,
解得:y=43.
即2点43分时回家
所以14点43分-8点43分=6点.
答:共用了6个小时.
【分析】(1)找到线段AB的四等分点,即可作出;
(2)根据线段之间的关系即可求出所有线段的长度;
(3)所有线段的长度和为:AC+AD+AE+AB+CD+CE+CB+DE+DB+EB,把这些线段转化成AB、CE的关系,即可求出所有线段的长度和.
解:(1)共10条线段,
;
(2)所有线段的和为:3+6+9+12+3+6+9+3+6+9=60.
(3)图中所有线段的长度和为:AC+AD+AE+AB+CD+CE+CB+DE+DB+EB,
=(AC+CD+DE+EB)+AB+CE+(AD+DB)+(AE+CB),
=AB+AB+CE+AB+(AB-BE+CB),
=2AB+CE+2AB+CE,
=4AB+2CE,
=4×12+2×2,
=52.
【分析】(1)根据点M、N分别是AC、BC的中点,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度即可,
(2)根据点M、N分别是AC、BC的中点,可知CM=AC,CN=BC,再利用MN=CM+CN即可求出MN的长度.
解:(1)∵点M、N分别是AC、BC的中点,
∴CM=AC=4cm,
CN=BC=2cm,
∴MN=CM+CN=4+2=6cm,
(2)猜测MN=a,
∵点M、N分别是AC、BC的中点,
∴CM=AC,
CN=BC,
∴MN=CM+CN=(AC+BC)=a.
【分析】(1)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(3)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案.
解:(1)由M、N分别是AC、BC的中点,
得MC=AC,CN=BC.
由线段的和差,得MN=MC+CN=AC+BC=×12+×10=6+5=11cm;
(2)MN=,理由如下:
由M、N分别是AC、BC的中点,
得MC=AC,CN=BC.
由线段的和差,得MN=MC+CN=AC+BC=(AC+BC)=cm;
(3)MN=,理由如下:
由M、N分别是AC、BC的中点,得MC=AC,CN=BC.
由线段的和差,得MN=MC﹣CN=AC﹣BC=(AC﹣BC)=cm;
如图:
只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
【分析】(1)直接利用角平分线的作法得出符合题意的图形;
(2)直接利用互余的性质结合角平分线的性质得出,∠A与∠EDF的关系.
解:(1)如图所示:
(2)∠A与∠EDF相等,
理由:∵∠B+∠BDF=90°,∠A+∠B=90°,
∴∠A=∠BDF,
∵DF平分∠BDE,
∴∠BDF=∠EDF,
∴∠A=∠EDF.
【分析】(1)根据角平分线的定义可以求得∠MON=(∠AOB+∠BOD);
(2)根据图示可以求得:∠BOD=∠BOC+∠COD=40°.然后结合角平分线的定义推知∠BON=∠BOD,∠COM=∠AOC.则∠MON=∠MOB+∠BON=40°;
(3)根据(1)、(2)的解题思路得到:
解:(1)如图2,∵OM,ON分别是∠AOC,∠BOD的角平分线,
∴∠BOM=∠AOB,∠BON=∠BOD,
∴∠MON=(∠AOB+∠BOD).
又∵∠AOB=50°,∠COD=30°,
∴∠MON=(∠AOB+∠BOD)=×(50°+30°)=40°.
故答案是:40°;
(2)如图3,∵∠BOD=∠BOC+∠COD=10°+30°=40°,ON平分∠BOD,
∴∠BON=∠BOD=×40°=20°.
∵∠AOC=∠BOC+∠AOB=10°+50°=60°,OM平分∠AOC,
∴∠COM=∠AOC=×60°=30°.
∴∠BOM=∠COM﹣∠BOC=30°﹣10°=20°.
∴∠MON=∠MOB+∠BON=20°+20°=40°;
(3)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,
∴∠MON=α+β=(α+β);
同理,当∠AOB是钝角时,∠MON=180°(α+β);
故答案是:或180°﹣.
(
第
2
页
共
2
页
)版权所有@21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
21世纪教育网 –中小学教育资源及组卷应用平台
图形的认识单元检测B卷
姓名:__________班级:__________学号:__________
、选择题(本大题共12小题,每小题4分,共48分 )
下面的几何体中,属于棱柱的有( )
A.1 个 B.2 个 C.3 个 D.4 个
如图,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A. 62° B. 118° C. 72° D. 59°
如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
A. B. C. D.
某校七年级在下午3:00开展“阳光体育”活动.下午3:00这一时刻,时钟上分针与时针所夹的角等于( )
A.30° B.60° C.90° D.120°
下列说法中正确的个数为( )
(1)过两点有且只有一条直线;
(2)连接两点的线段叫两点间的距离;
(3)两点之间所有连线中,线段最短;
(4)射线比直线小一半.
A.1个 B.2个 C.3个 D.4个
如图所示,用量角器度量∠AOB,可以读出∠AOB的度数为( )
A. 45° B. 55° C. 125° D. 135°
下列结论中,不正确的是( )
A.两点确定一条直线 B.两点之间,直线最短
C.等角的余角相等 D.等角的补角相等
平面上有三个点,可以确定直线的条数是 ( )
A.1条 B.2条 C.3条 D.1条或3条
某公司员工分别在A.B、C三个住宅区,A区有30人,B区有30人,C区有10人,三个区在同一条直线上,如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
A.A区 B.B区 C.C区 D.A.B两区之间
已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC等于( )
A.120° B.120°或60° C.30° D.30°或90°
已知线段AB=6cm,若M是AB的三等分点,N是AM的中点,则线段MN的长度为( )
A.1cm B.2cm C.1.5cm D.1cm或2cm
挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走。如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走( )
A.②号棒 B.⑦号棒 C.⑧号棒 D.⑩号棒
、填空题(本大题共6小题,每小题4分,共24分)
如图,已知线段AC,点D为AC的中点,BC=AB,BD=1cm,则AC=__________.
如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=40°,则∠AOC= °.
要把一根木条在墙上钉牢,至少需要__________枚钉子.其中的道理是__________.
一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字﹣1、﹣2、﹣3、﹣4、﹣5、﹣6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc= .
如图,已知点C在线段AB上,AC=3cm,BC=2cm,点M、N分别是AC、BC的中点,则线段MN的长度为 cm.
如图,一工作流程线上有6位工人,他们的工作位置分别是A.B、C、D、E、F,现要在这六个位置之一设置一个工具箱,使工人取工具所花费的总时间最少.那么这个工具箱应放置在 最合适.
、解答题(本大题共8小题,共78分)
在同一个学校上学的小明、小伟、小红三位同学住在A,B,C三个住宅区,如图所示(A,B,C在同一条直线上),且AB=60米,BC=100米,他们打算合租一辆接送车去上学,由于车位紧张,准备在周围只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在哪里?并说明理由.
OC是从∠AOB的顶点O引出的一条射线,若∠AOB=90°,∠AOB=2∠BOC,求∠AOC的度数.
地震后,许许多多志愿者到灾区投入了抗震救灾行列中.志愿者小方八点多准备前去为灾民服务,临出门他一看钟,时针与分针正好是重合的,下午两点多他拖着疲惫的身体回到家中,一进门看见钟的时针与分针方向相反,正好成一条直线,问小方是几点钟去为灾民服务?几点钟回到家?共用了多少时间?
在线段AB上顺次取三点C、D、E.
(1)若C、D、E是AB的四个等分点,画出图形,并求图中所有线段条数;
(2)若AB=12,求(1)中所有线段的长度;
(3)当C、D、E是线段上顺次三点时,若AB=12.CE=2,求图中所有线段的长度和.
如图,点C在线段AB上,线段AC=8cm,BC=4cm,点M、N分别是AC、BC的中点,求:
(1)线段MN的长度.
(2)根据(1)的计算过程和结果,设AC+BC=a,其它条件不变,你能猜测出MN的长度吗?请证明你的猜测.
如图,点C在AB上,点M、N分别是AC、BC的中点,
(1)若AC=12cm,BC=10cm,求线段MN的长;
(2)若点C为线段AB上任意一点,满足AC+BC=acm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若点C在线段AB的延长线上,且满足AC﹣BC=bcm,点M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.请用一句简洁的话描述你发现的结论.
如图,∠A+∠B=90°,点D在线段AB上,点E在线段AC上,作直线DE,DF平分∠BDE,DF与BC交于点F.
(1)依题意补全图形;
(2)当∠B+∠BDF=90°时,∠A与∠EDF是否相等?说明理由.
如图1,∠AOB=α,∠COD=β,OM,ON分别是∠AOC,∠BOD的角平分线.
(1)若∠AOB=50°,∠COD=30°,当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图2),则∠MON的大小为__________;
(2)在(1)的条件下,继续绕着点O逆时针旋转∠COD,当∠BOC=10°时(如图3),求∠MON的大小并说明理由;
(3)在∠COD绕点O逆时针旋转过程中,∠MON=__________.(用含α,β的式子表示).
答案解析
、选择题
解:从左到右依次是长方体,圆柱,棱柱,棱锥,圆锥,棱柱. 故选:C.
【分析】利用对顶角的定义以及周角定义得出∠AOC的度数.
解:∵直线AB和CD相交于点O,∠AOD与∠BOC的和为236°,
∴∠AOC=∠BOD==62°.
故选A.
【分析】将A.B、C、D分别展开,能和原图相对应的即为正确答案.
解:A.展开得到,不能和原图相对应,故本选项错误;
B、展开得到,能和原图相对,故本选项正确;
C、展开得到,不能和原图相对应,故本选项错误;
D、展开得到,不能和原图相对应,故本选项错误.
故选B.
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,借助图形,找出时针和分针之间相差的大格数,用大格数乘30°即可.
解:∵3点整,时针指向3,分针指向12.
钟表12个数字,每相邻两个数字之间的夹角为30°,
∴3点整分针与时针的夹角正好是30°×3=90°.
故选:C.
【分析】 根据直线、射线等相关的定义或定理分别判断得出答案即可.
解:(1)过两点有且只有一条直线,此选项正确;
(2)连接两点的线段的长度叫两点间的距离,此选项错误;
(3)两点之间所有连线中,线段最短,此选项正确;
(4)射线比直线小一半,根据射线与直线都无限长,故此选项错误;
故正确的有2个.
故选:B.
解:由生活知识可知这个角小于90度,排除C、D,又OB边在50与60之间,所以,度数应为55°。
故选:B.
【分析】 根据线段的性质:两点之间线段最短,可以确定“两点之间,直线最短”是错误的.
解:A.公理.
B、两点之间,线段最短.
C、等角的余角相等.
D、等角的补角相等.
故选B.
【分析】分别从若平面内的三个点A.B、C不在同一直线上与若平面内的三个点A.B、C在同一直线上去分析,则可求得答案.
解:∵若平面内的三个点A.B、C不在同一直线上,则能确定的直线的条数是:3条;
若平面内的三个点A.B、C在同一直线上,则能确定的直线的条数是:1条.
∴平面内的三个点A.B、C能确定的直线的条数是:1条或3条.
故选D.
【分析】分①设在A区、B区之间时,设距离A区x米,表示出所有员工的步行总路程之和,然后求出最小值,②设在B区、C区之间时,设距离B区x米,表示出所有员工的步行总路程之和,然后求出最小值,比较即可得解.
解:①设在A区、B区之间时,设距离A区x米,
则所有员工步行路程之和=30x+30(100-x)+10(100+200-x),
=30x+3000-30x+3000-10x,
=-10x+6000,
∴当x最大为100时,即在B区时,路程之和最小,为5000米;
②设在B区、C区之间时,设距离B区x米,
则所有员工步行路程之和=30(100+x)+30x+10(200-x),
=3000+30x+30x+2000-10x,
=50x+5000,
∴当x最大为0时,即在B区时,路程之和最小,为5000米;
综上所述,停靠点的位置应设在B区.
故选B.
【分析】 此题需要分类讨论,共两种情况.先作图后计算.
解:∵∠BOC=30°,∠AOB=3∠BOC,
∴∠AOB=3×30°=90°
(1)当OC在∠AOB的外侧时,
∠AOC=∠AOB+∠BOC=90°+30°=120度;
(2)当OC在∠AOB的内侧时,
∠AOC=∠AOB﹣∠BOC=90°﹣30°=60度.
故选:B.
【分析】根据M是AB的三等分点,可得AM的长,再根据线段中点的性质,可得答案.
解:由线段AB=6cm,若M是AB的三等分点,得
AM=2,或AM=4.
当AM=2cm时,由N是AM的中点,得MN=AM=×2=1(cm);
当AM=4cm时,由N是AM的中点,得MN=AM=×4=2(cm);
故选:D.
【分析】 本题考查动手实践操作能力和空间想象能力,体现了做数学的数学思想方法。按照条件中的游戏规则,第1次应拿走9号棒、第2次应拿走5号棒,第3次应拿走6号棒,第4次应拿走2号棒,第5次应拿走8号棒,第6次应拿走10号棒,第7次应拿走7号棒,第8次应拿走3号棒,第9次应拿走4号棒,第10次应拿走1号棒,
从图中看,可知从上到下的棒的序号依次是⑨⑤⑥②⑧⑩⑦③④①,因此第6次应拿走⑩号棒;
故选D
、填空题
【分析】根据线段中点的性质,可得DC=AC,根据BC=AB,可得BC与AC的关系,根据线段的和差,可得答案.
解:由点D为AC的中点,得
DC=AC.
由BC=AB,得
AB=2BC,AC=BC+AB=3BC,
BCAC,
由线段的和差,得
BD=CD﹣BC,即AC﹣AC=1,
解得AC=6cm,
故答案为:6cm.
【分析】根据∠AOD是∠BOD的补角求得∠AOD的度数,然后根据角平分线的定义求∠AOC的度数.
解:∵∠AOD+∠BOD=180°,∠BOD=40°,
∴∠AOD=140°;
∵OC平分∠AOD,
∴∠AOC=∠COD=∠AOD=70°;
故答案是:70.
【分析】根据两点确定一条直线解答.
解:把一根木条钉牢在墙上,至少需要两枚钉子,其中的道理是:两点确定一条直线.
故答案为:两,两点确定一条直线.
【分析】先根据图中正方形的摆放方式可知与白色面相邻的面有紫、蓝、绿、红,然后再确定出其中相对的面,从而得出a、b、c的值,最后代入计算即可.
解:∵根据图形可知:白色面相邻的面有紫、蓝、绿、红,
∴“紫”与“绿”是对面,“红”与“蓝”是对面,“白”与“黄”是对面.
∴第一个正方体的底面是黄色,第二个正方体的底面是紫色,第三个正方体的底面是绿色.
∴a=﹣3,b=﹣6,c=﹣4.
∴a+b+c+abc=(﹣3)+(﹣6)+(﹣4)+(﹣3)×(﹣6)×(﹣4)=﹣13+(﹣72)=﹣85.
故答案为:﹣85.
【分析】由已知条件可知,MN=MC+NC,又因为点M、N分别是AC、BC的中点,则MC=AC,NC=BC,故MN=MC+NC=(AC+BC)=AB.
解:∵AC=3cm,BC=2cm,
点M、N分别是AC、BC的中点,
∴MC=cm,NC=1cm,
∴MN=MC+NC=cm.
【分析】总时间最少就是总路程最短.因此可采用分类讨论的思想,假设工具箱分别设置在A.B、C、D、E、F的位置,根据图示求出设置在以上位置时工人经过的总路程,然后进行比较,总路程最短的即为正确答案.
解:如设在A点,总路程为:5AB+4BC+3CD+2DE+EF;
如设在B点,总路程为:AB+4BC+3CD+2DE+EF;
如设在C点,总路程为:AB+2BC+3CD+2DE+EF;
如设在D点,总路程为:AB+2BC+3CD+2DE+EF;
如设在E点,总路程为:AB+2BC+3CD+4DE+EF;
如设在F点,总路程为:AB+2BC+3CD+4DE+EF;
通过比较可以发现,如设在C点和D点总路程最短,所以花费的总时间最少.
故答案为:C或D的位置.
、解答题
【分析】根据小明、小红步行的距离之和为A.C两点间的距离不变,判断出小伟步行的距离最小时,三人的总路程之和最小解答.
解:停靠点设在B点时,三位同学步行到停靠点的路程之和最小,
是60+100=160米,
理由如下:小明、小红步行的距离之和为A.C两点间的距离不变,
小伟步行的距离是0米时,三位同学步行到停靠点的路程之和最小.
【分析】利用角的和差关系计算,注意此题要分两种情况.
解:①如图1所示,OC在∠AOB内部,
∵∠AOB=90°,∠AOB=2∠BOC,
∴∠BOC=×90°=45°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣45°=45°;
②如图2所示,OC在∠AOB外部,
∵∠AOB=90°,∠AOB=2∠BOC,
∴∠BOC=×90°=45°,
又∵∠AOC=∠AOB+∠BOC,
∴∠AOC=90°+45°=135°.
【分析】在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动()°依据这一关系列出方程,可以求出.
解:设8点x分时针与分针重合,
则:x-=40,
解得:x=43.
即8点43分时出门.
设2点y分时,时针与分针方向相反.
则:y-=10+30,
解得:y=43.
即2点43分时回家
所以14点43分-8点43分=6点.
答:共用了6个小时.
【分析】(1)找到线段AB的四等分点,即可作出;
(2)根据线段之间的关系即可求出所有线段的长度;
(3)所有线段的长度和为:AC+AD+AE+AB+CD+CE+CB+DE+DB+EB,把这些线段转化成AB、CE的关系,即可求出所有线段的长度和.
解:(1)共10条线段,
;
(2)所有线段的和为:3+6+9+12+3+6+9+3+6+9=60.
(3)图中所有线段的长度和为:AC+AD+AE+AB+CD+CE+CB+DE+DB+EB,
=(AC+CD+DE+EB)+AB+CE+(AD+DB)+(AE+CB),
=AB+AB+CE+AB+(AB-BE+CB),
=2AB+CE+2AB+CE,
=4AB+2CE,
=4×12+2×2,
=52.
【分析】(1)根据点M、N分别是AC、BC的中点,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度即可,
(2)根据点M、N分别是AC、BC的中点,可知CM=AC,CN=BC,再利用MN=CM+CN即可求出MN的长度.
解:(1)∵点M、N分别是AC、BC的中点,
∴CM=AC=4cm,
CN=BC=2cm,
∴MN=CM+CN=4+2=6cm,
(2)猜测MN=a,
∵点M、N分别是AC、BC的中点,
∴CM=AC,
CN=BC,
∴MN=CM+CN=(AC+BC)=a.
【分析】(1)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(3)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案.
解:(1)由M、N分别是AC、BC的中点,
得MC=AC,CN=BC.
由线段的和差,得MN=MC+CN=AC+BC=×12+×10=6+5=11cm;
(2)MN=,理由如下:
由M、N分别是AC、BC的中点,
得MC=AC,CN=BC.
由线段的和差,得MN=MC+CN=AC+BC=(AC+BC)=cm;
(3)MN=,理由如下:
由M、N分别是AC、BC的中点,得MC=AC,CN=BC.
由线段的和差,得MN=MC﹣CN=AC﹣BC=(AC﹣BC)=cm;
如图:
只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
【分析】(1)直接利用角平分线的作法得出符合题意的图形;
(2)直接利用互余的性质结合角平分线的性质得出,∠A与∠EDF的关系.
解:(1)如图所示:
(2)∠A与∠EDF相等,
理由:∵∠B+∠BDF=90°,∠A+∠B=90°,
∴∠A=∠BDF,
∵DF平分∠BDE,
∴∠BDF=∠EDF,
∴∠A=∠EDF.
【分析】(1)根据角平分线的定义可以求得∠MON=(∠AOB+∠BOD);
(2)根据图示可以求得:∠BOD=∠BOC+∠COD=40°.然后结合角平分线的定义推知∠BON=∠BOD,∠COM=∠AOC.则∠MON=∠MOB+∠BON=40°;
(3)根据(1)、(2)的解题思路得到:
解:(1)如图2,∵OM,ON分别是∠AOC,∠BOD的角平分线,
∴∠BOM=∠AOB,∠BON=∠BOD,
∴∠MON=(∠AOB+∠BOD).
又∵∠AOB=50°,∠COD=30°,
∴∠MON=(∠AOB+∠BOD)=×(50°+30°)=40°.
故答案是:40°;
(2)如图3,∵∠BOD=∠BOC+∠COD=10°+30°=40°,ON平分∠BOD,
∴∠BON=∠BOD=×40°=20°.
∵∠AOC=∠BOC+∠AOB=10°+50°=60°,OM平分∠AOC,
∴∠COM=∠AOC=×60°=30°.
∴∠BOM=∠COM﹣∠BOC=30°﹣10°=20°.
∴∠MON=∠MOB+∠BON=20°+20°=40°;
(3)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,
∴∠MON=α+β=(α+β);
同理,当∠AOB是钝角时,∠MON=180°(α+β);
故答案是:或180°﹣.
(
第
2
页
共
2
页
)版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
