13.3.1 等腰三角形课件+教案+练习
文档属性
| 名称 | 13.3.1 等腰三角形课件+教案+练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-16 00:00:00 | ||
图片预览










文档简介
课件40张PPT。13.3.1等腰三角形
本课说明在已经学习了三角形的基本概念、全等三角形和轴对称知识的基础上,进一步研究特殊的三角形——等腰三角形,研究等腰三角形的底角、底边上的中线、顶角平分线、底边上的高所具有的性质.探索等腰三角形的判定方法,这为我们提供了证明两条线段相等的新方法.
学习说明学习目标:
1.探索并证明等腰三角形的两个性质.
2.能利用性质证明两个角相等或两条线段相等.
3.结合等腰三角形性质的探索与证明过程,体会轴
对称在研究几何问题中的作用.
4.探索等腰三角形判定定理.
5.理解等腰三角形的判定定理,并会运用其进行简
单的证明.
6.了解等腰三角形的尺规作图.学习重点:
1.探索并证明等腰三角形性质.
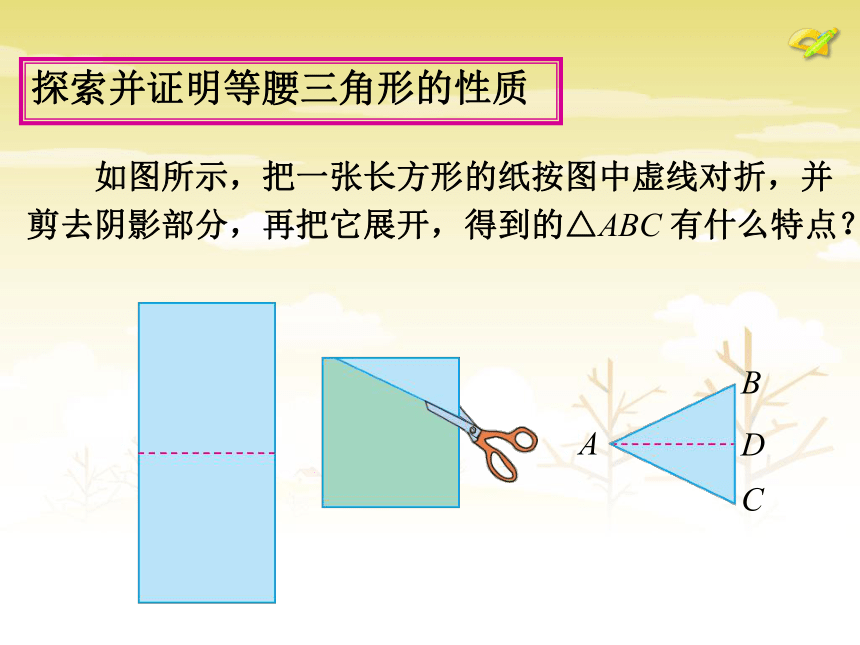
2.理解和运用等腰三角形的判定定理. 学习说明 如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?探索并证明等腰三角形的性质 探索并证明等腰三角形的性质 仔细观察自己剪出的等腰三角形纸片,你能发现这
个等腰三角形有什么特征吗? 等腰三角形的特征:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.探索并证明等腰三角形的性质 同学们剪下的等腰三角形纸片大小不同,形状各
异,是否都具有上述所概括的特征?探索并证明等腰三角形的性质 在练习本上任意画一个等腰三角形,把它剪下来,
折一折,上面得出的结论仍然成立吗?由此你能概括出
等腰三角形的性质吗?探索并证明等腰三角形的性质 探索并证明等腰三角形的性质 等腰三角形的性质:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合. 利用实验操作的方法,我们发现并概括出等腰三角
形的性质1和性质2.对于性质1,你能通过严格的逻辑
推理证明这个结论吗?
(1)你能根据结论画出图形,写出已知、求证吗?
(2)结合所画的图形,你认为证明两个底角相等的思
路是什么?
(3)如何在一个等腰三角形中构造出两个全等三角形
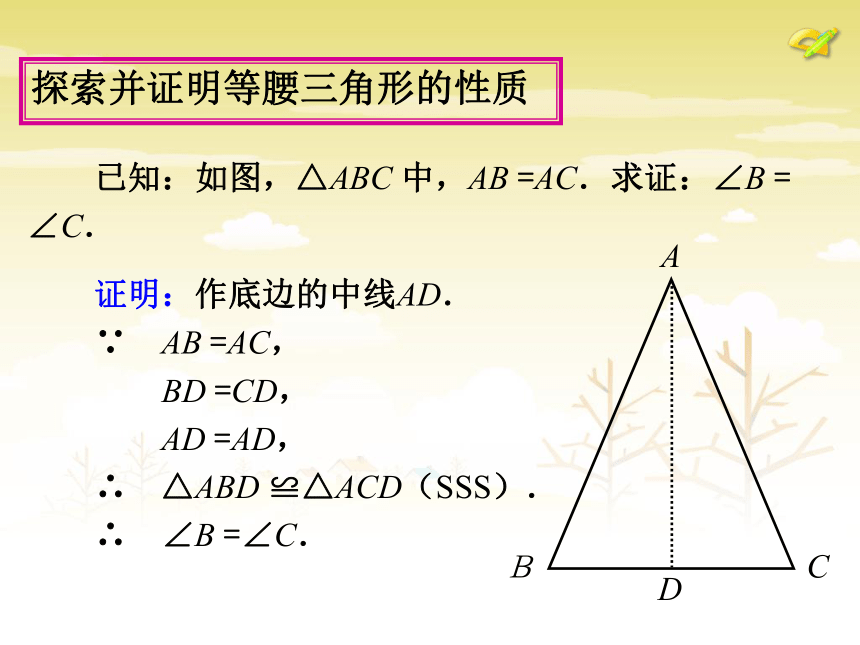
呢?从剪图、折纸的过程中你能获得什么启发? 探索并证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC.求证:∠B =
∠C.探索并证明等腰三角形的性质 证明:作底边的中线AD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).
∴ ∠B =∠C. 你还有其他方法证明性质1吗?探索并证明等腰三角形的性质 可以作底边的高线或顶角的角平分线. 性质2可以分解为三个命题,本节课证明“等腰三
角形的底边上的中线也是底边上的高和顶角平分线”.探索并证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC.探索并证明等腰三角形的性质 证明:∵ AD 是底边BC 的中线,
∴ BD =CD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).探索并证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.探索并证明等腰三角形的性质 在等腰三角形性质的探索过程和证明过程中,“折
痕”“辅助线”发挥了非常重要的作用,由此,你能发
现等腰三角形具有什么特征?
等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴. 例1 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.探索并证明等腰三角形的性质 问题 等腰三角形性质定理的内容是什么?这个命
题的题设和结论分别是什么? 性质定理的条件是:一个三角形中有两条边相等. 结论:这两条边所对的角相等. 探索等腰三角形的判定定理 作顶角的平分线或底边上的高或底边的中线,将一
个三角形的问题转化为两个全等三角形来证明两个角相等. 探索等腰三角形的判定定理 思考 性质定理证明方法是什么? 探索等腰三角形的判定定理 问题 一个三角形满足什么条件是等腰三角形? 这两个角所对的边相等. 探索等腰三角形的判定定理 思考1 如果一个三角形有两个角相等,那么这两
个角所对的边有什么关系? 题设:一个三角形有两个角相等.
结论:这两个角所对的边相等. 探索等腰三角形的判定定理 思考2 这个命题的题设和结论又分别是什么呢?
如何证明这个命题?探索等腰三角形的判定定理 问题 类比等腰三角形性质定理的证明方法,你能
选择一种来证明这个命题吗? 证明:过A 点作AE⊥BC,垂足为E.
在△ABE 和△ACE 中,探索等腰三角形的判定定理∴ △ABE ≌△ACE .
∴ AB = AC . 追问 你还有其他证明方法吗? 已知:如图,在△ABC 中,∠B =∠C. 求证:AB
=AC. 思考 与等腰三角形性质进
行比较看有什么区别?探索等腰三角形的判定定理 等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对
的边也相等(简写成“等角对等边”).符号语言:
∵ 在△ABC 中,∠B =∠C,
∴ AB =AC.巩固等腰三角形的判定定理 例2 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形. 巩固等腰三角形的判定定理 已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥
BC.
求证:AB =AC.巩固等腰三角形的判定定理(1)AB、AC 在同一个三角形中,
应选择“等角对等边”;
(2)建立三角形的外角和与之不相
邻的内角关系;
(3)利用平行转移已知角;最终使
得相等的角转化到同一个三角
形中. 追问 要证明AB =AC,应如何选择证明方法? 证明:∵ AD∥BC ,
∴ ∠1 =∠B
( ),
∠2 =∠C
( ).巩固等腰三角形的判定定理 已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥
BC.
求证:AB =AC.两直线平行,同位角相等两直线平行,内错角相等等边对等角巩固等腰三角形的判定定理 已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥
BC.
求证:AB =AC.证明:∵ ∠1 =∠2,
∴ ∠B =∠C.
∴ AB =AC
( ).D巩固等腰三角形的判定定理 例3 已知等腰三角形底边长为a ,底边上的高的
长为h ,求作这个等腰三角形. 作法:
(1)作线段AB =a;
(2)作线段AB 的垂直平分线MN,与
AB 相交于点D;
(3)在MN上取一点C,使DC =h;
(4)连接AC,BC,则△ABC 就是所
求作的等腰三角形.课堂练习 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= °;课堂练习 练习1 填空:
(2)如图,△ABC 中, AB =AC, ∠A=120°, 则∠B
= °; 课堂练习 练习2 如图,△ABC 是等腰直角三角形(AB =
AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,
∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的
线段.课堂练习 练习3 如图,把一张长方形的纸沿着对角线折叠,
重合部分是一个等腰三角形吗?为什么?课堂练习 练习4 求证:如果三角形一条边上的中线等于这
条边的一半,那么这个三角形是直角三角形.课堂练习 练习5 如图,AC 和BD 相交于点O,且AB∥DC,
OA =OB.求证:OC =OD.(4)等腰三角形的判定方法有哪几种?
(5)结合本节课的学习,谈谈等腰三角形性质和判
定的区别和联系.课堂小结(1)本节课学习了哪些主要内容?
(2)我们是怎么探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法? 教科书习题13.3第1、2、3、4、5、6题.布置作业
学习说明学习目标:
1.探索并证明等腰三角形的两个性质.
2.能利用性质证明两个角相等或两条线段相等.
3.结合等腰三角形性质的探索与证明过程,体会轴
对称在研究几何问题中的作用.
4.探索等腰三角形判定定理.
5.理解等腰三角形的判定定理,并会运用其进行简
单的证明.
6.了解等腰三角形的尺规作图.学习重点:
1.探索并证明等腰三角形性质.
2.理解和运用等腰三角形的判定定理. 学习说明 如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?探索并证明等腰三角形的性质 探索并证明等腰三角形的性质 仔细观察自己剪出的等腰三角形纸片,你能发现这
个等腰三角形有什么特征吗? 等腰三角形的特征:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.探索并证明等腰三角形的性质 同学们剪下的等腰三角形纸片大小不同,形状各
异,是否都具有上述所概括的特征?探索并证明等腰三角形的性质 在练习本上任意画一个等腰三角形,把它剪下来,
折一折,上面得出的结论仍然成立吗?由此你能概括出
等腰三角形的性质吗?探索并证明等腰三角形的性质 探索并证明等腰三角形的性质 等腰三角形的性质:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合. 利用实验操作的方法,我们发现并概括出等腰三角
形的性质1和性质2.对于性质1,你能通过严格的逻辑
推理证明这个结论吗?
(1)你能根据结论画出图形,写出已知、求证吗?
(2)结合所画的图形,你认为证明两个底角相等的思
路是什么?
(3)如何在一个等腰三角形中构造出两个全等三角形
呢?从剪图、折纸的过程中你能获得什么启发? 探索并证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC.求证:∠B =
∠C.探索并证明等腰三角形的性质 证明:作底边的中线AD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).
∴ ∠B =∠C. 你还有其他方法证明性质1吗?探索并证明等腰三角形的性质 可以作底边的高线或顶角的角平分线. 性质2可以分解为三个命题,本节课证明“等腰三
角形的底边上的中线也是底边上的高和顶角平分线”.探索并证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC.探索并证明等腰三角形的性质 证明:∵ AD 是底边BC 的中线,
∴ BD =CD.
∵ AB =AC,
BD =CD,
AD =AD,
∴ △ABD ≌△ACD(SSS).探索并证明等腰三角形的性质 已知:如图,△ABC 中,AB =AC,AD 是底边BC
的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.探索并证明等腰三角形的性质 在等腰三角形性质的探索过程和证明过程中,“折
痕”“辅助线”发挥了非常重要的作用,由此,你能发
现等腰三角形具有什么特征?
等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴. 例1 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.探索并证明等腰三角形的性质 问题 等腰三角形性质定理的内容是什么?这个命
题的题设和结论分别是什么? 性质定理的条件是:一个三角形中有两条边相等. 结论:这两条边所对的角相等. 探索等腰三角形的判定定理 作顶角的平分线或底边上的高或底边的中线,将一
个三角形的问题转化为两个全等三角形来证明两个角相等. 探索等腰三角形的判定定理 思考 性质定理证明方法是什么? 探索等腰三角形的判定定理 问题 一个三角形满足什么条件是等腰三角形? 这两个角所对的边相等. 探索等腰三角形的判定定理 思考1 如果一个三角形有两个角相等,那么这两
个角所对的边有什么关系? 题设:一个三角形有两个角相等.
结论:这两个角所对的边相等. 探索等腰三角形的判定定理 思考2 这个命题的题设和结论又分别是什么呢?
如何证明这个命题?探索等腰三角形的判定定理 问题 类比等腰三角形性质定理的证明方法,你能
选择一种来证明这个命题吗? 证明:过A 点作AE⊥BC,垂足为E.
在△ABE 和△ACE 中,探索等腰三角形的判定定理∴ △ABE ≌△ACE .
∴ AB = AC . 追问 你还有其他证明方法吗? 已知:如图,在△ABC 中,∠B =∠C. 求证:AB
=AC. 思考 与等腰三角形性质进
行比较看有什么区别?探索等腰三角形的判定定理 等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对
的边也相等(简写成“等角对等边”).符号语言:
∵ 在△ABC 中,∠B =∠C,
∴ AB =AC.巩固等腰三角形的判定定理 例2 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形. 巩固等腰三角形的判定定理 已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥
BC.
求证:AB =AC.巩固等腰三角形的判定定理(1)AB、AC 在同一个三角形中,
应选择“等角对等边”;
(2)建立三角形的外角和与之不相
邻的内角关系;
(3)利用平行转移已知角;最终使
得相等的角转化到同一个三角
形中. 追问 要证明AB =AC,应如何选择证明方法? 证明:∵ AD∥BC ,
∴ ∠1 =∠B
( ),
∠2 =∠C
( ).巩固等腰三角形的判定定理 已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥
BC.
求证:AB =AC.两直线平行,同位角相等两直线平行,内错角相等等边对等角巩固等腰三角形的判定定理 已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥
BC.
求证:AB =AC.证明:∵ ∠1 =∠2,
∴ ∠B =∠C.
∴ AB =AC
( ).D巩固等腰三角形的判定定理 例3 已知等腰三角形底边长为a ,底边上的高的
长为h ,求作这个等腰三角形. 作法:
(1)作线段AB =a;
(2)作线段AB 的垂直平分线MN,与
AB 相交于点D;
(3)在MN上取一点C,使DC =h;
(4)连接AC,BC,则△ABC 就是所
求作的等腰三角形.课堂练习 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= °;课堂练习 练习1 填空:
(2)如图,△ABC 中, AB =AC, ∠A=120°, 则∠B
= °; 课堂练习 练习2 如图,△ABC 是等腰直角三角形(AB =
AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,
∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的
线段.课堂练习 练习3 如图,把一张长方形的纸沿着对角线折叠,
重合部分是一个等腰三角形吗?为什么?课堂练习 练习4 求证:如果三角形一条边上的中线等于这
条边的一半,那么这个三角形是直角三角形.课堂练习 练习5 如图,AC 和BD 相交于点O,且AB∥DC,
OA =OB.求证:OC =OD.(4)等腰三角形的判定方法有哪几种?
(5)结合本节课的学习,谈谈等腰三角形性质和判
定的区别和联系.课堂小结(1)本节课学习了哪些主要内容?
(2)我们是怎么探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法? 教科书习题13.3第1、2、3、4、5、6题.布置作业
