第三章 位置与坐标单元检测题A
图片预览



文档简介
北师版数学八年级上册第3章《位置与坐标》单元检测题A
一.选择题
1.点P(1,﹣2)关于y轴对称的点的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(﹣2,1)
2.如图在正方形网格中,若A(1,1),B(2,0),则C点的坐标为( )
A.(﹣3,﹣2) B.(3,﹣2) C.(﹣2,﹣3) D.(2,﹣3)
3.如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(﹣1,1),(﹣3,1),(﹣1,﹣1).30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
A.Q′(2,3),R′(4,1) B.Q′(2,3),R′(2,1)
C.Q′(2,2),R′(4,1) D.Q′(3,3),R′(3,1)
4.已知点P(1﹣2m,m﹣1),则不论m取什么值,该P点必不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,点P(m﹣3,4﹣2m)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)
7.在平面直角坐标系中,点P(1,2)到原点的距离是( )
A.1 B. C. D.
8.已知点A(m,1)与点B(5,n)关于原点对称,则m和n的值为( )
A.m=5,n=﹣1 B.m=﹣5,n=1 C.m=﹣1,n=﹣5 D.m=﹣5,n=﹣1
9.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
A.(﹣2,1) B.(﹣1,1) C.(1,﹣2) D.(﹣1,﹣2)
10.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(﹣1,﹣1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,﹣1),则点B′的坐标为( )
A.(4,2) B.(5,2) C.(6,2) D.(5,3)
11.如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是( )
A.(5,0) B.(8,0) C.(0,5) D.(0,8)
二.填空题
12.在平面直角坐标系中有一点A(﹣2,1),将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为 .2·1·c·n·j·y
13.定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为 .
14.阅读材料:设=(x1,y1),=(x2,y2),如果∥,则x1?y2=x2?y1.根据该材料填空:已知=(2,3),=(4,m),且∥,则m= .
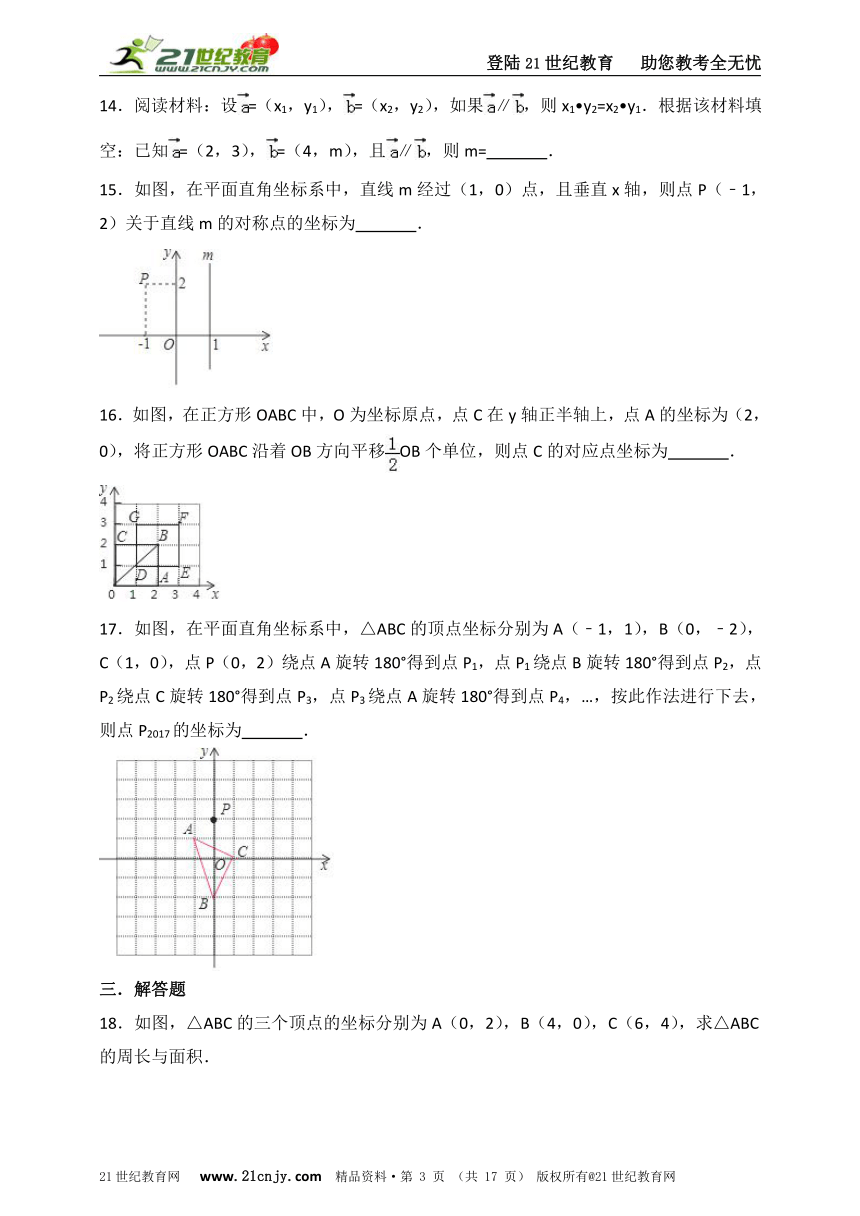
15.如图,在平面直角坐标系中,直线m经过(1,0)点,且垂直x轴,则点P(﹣1,2)关于直线m的对称点的坐标为 .
16.如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移OB个单位,则点C的对应点坐标为 .
17.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1),B(0,﹣2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为 .
三.解答题
18.如图,△ABC的三个顶点的坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
19.如图是一个平面直角坐标系,按要求完成下列各小题.
(1)写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标;
(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?
(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.
20.已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.
(1)点P在x轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
21.如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
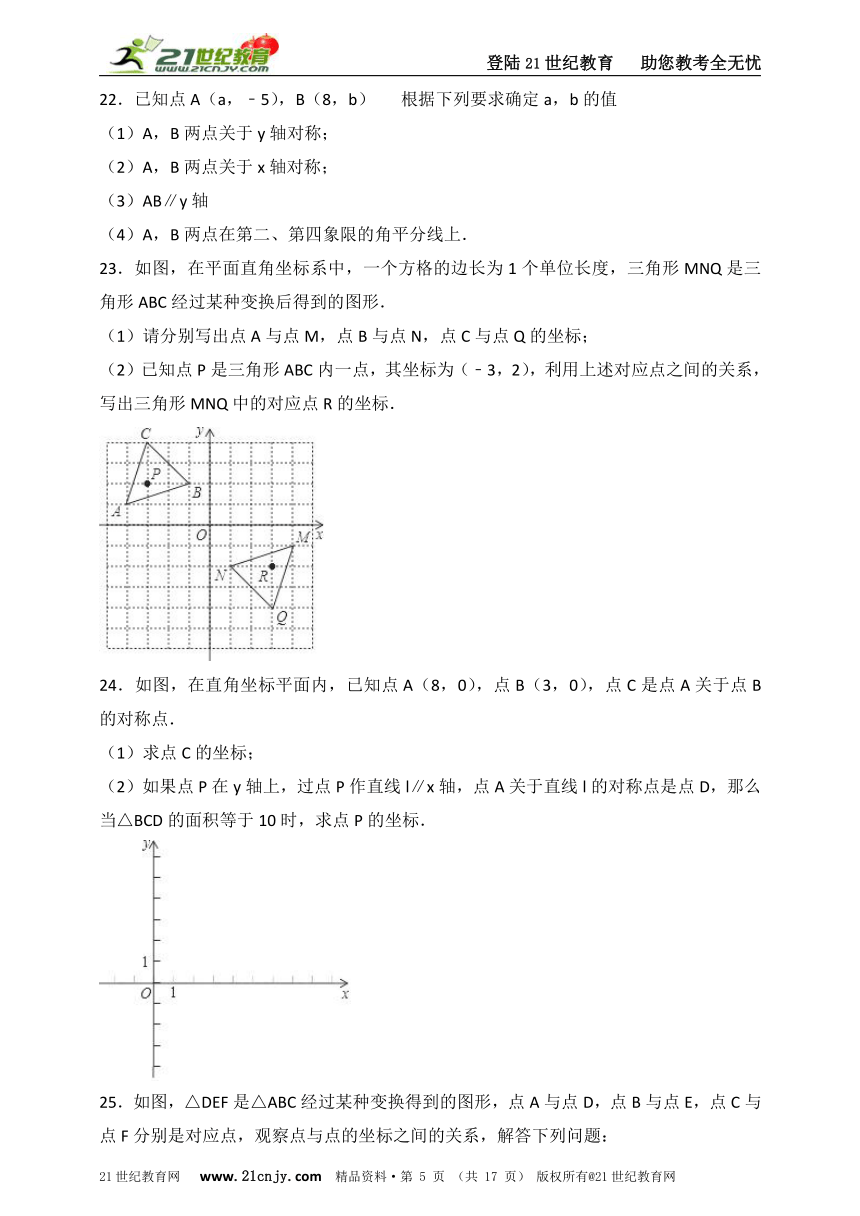
22.已知点A(a,﹣5),B(8,b) 根据下列要求确定a,b的值
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB∥y轴
(4)A,B两点在第二、第四象限的角平分线上.
23.如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.
(1)请分别写出点A与点M,点B与点N,点C与点Q的坐标;
(2)已知点P是三角形ABC内一点,其坐标为(﹣3,2),利用上述对应点之间的关系,写出三角形MNQ中的对应点R的坐标.
24.如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.
(1)求点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.
25.如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
26.问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;21·世纪*教育网
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
答案与解析
一.选择题
1.【分析】关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案.
【解答】解:P(1,﹣2)关于y轴对称的点的坐标是(﹣1,﹣2),
故选:C.
2.【分析】根据A(1,1),B(2,0),再结合图形即可确定出点C的坐标.
【解答】解:∵点A的坐标是:(1,1),
点B的坐标是:(2,0),
∴点C的坐标是:(3,﹣2).
故选B.
3.【分析】由点P(﹣1,1)到P′(4,3)知,编队需向右平移5个单位、向上平移2个单位,据此可得.www.21-cn-jy.com
【解答】解:由点P(﹣1,1)到P′(4,3)知,编队需向右平移5个单位、向上平移2个单位,
∴点Q(﹣3,1)的对应点Q′坐标为(2,3),点R(﹣1,﹣1)的对应点R′(4,1),
故选:A.
4.【分析】分横坐标是正数和负数两种情况求出m的值,再求出纵坐标的正负情况,然后根据各象限内点的坐标特征解答.
【解答】解:①1﹣2m>0时,m<,
m﹣1<0,
所以,点P在第四象限,一定不在第一象限;
②1﹣2m<0时,m>,
m﹣1既可以是正数,也可以是负数,
点P可以在第二、三象限,
综上所述,P点必不在第一象限.
故选A.
5.【分析】分点P的横坐标是正数和负数两种情况讨论求解.
【解答】解:①m﹣3>0,即m>3时,﹣2m<﹣6,
4﹣2m<﹣2,
所以,点P(m﹣3,4﹣2m)在第四象限,不可能在第一象限;
②m﹣3<0,即m<3时,﹣2m>﹣6,
4﹣2m>﹣2,
点P(m﹣3,4﹣2m)可以在第二或三象限,
综上所述,点P不可能在第一象限.
故选A.
6.【分析】由AC∥x轴,A(﹣2,2),根据坐标的定义可求得y值,根据线段BC最小,确定BC⊥AC,垂足为点C,进一步求得BC的最小值和点C的坐标.
【解答】解:依题意可得:
∵AC∥x,
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即
BC的最小值=5﹣2=3,
此时点C的坐标为(3,2),
故选D.
7.【分析】求出1与2的平方和的算术平方根即可.
【解答】解:点P(1,2)到原点的距离是=.
故选D.
8.【分析】根据关于原点对称,则两点的横、纵坐标都是互为相反数,可得答案.
【解答】解:点A(m,1)与点B(5,n)关于原点对称,得
m=﹣5,n=﹣1.
故选:D.
9.【分析】首先确定x轴、y轴的位置,然后根据轴对称图形的定义判断.
【解答】解:棋盘中心方子的位置用(﹣1,0)表示,则这点所在的横线是x轴,右下角方子的位置用(0,﹣1),则这点所在的纵线是y轴,则当放的位置是(﹣1,1)时构成轴对称图形.21·cn·jy·com
故选B.
10.【分析】根据A点的坐标及对应点的坐标可得线段AB向右平移4个单位,然后可得B′点的坐标.
【解答】解:∵A(﹣1,﹣1)平移后得到点A′的坐标为(3,﹣1),
∴向右平移4个单位,
∴B(1,2)的对应点坐标为(1+4,2),
即(5,2).
故选:B.
11.【分析】直接利用勾股定理得出AB的长,再利用旋转的性质得出OB′的长,进而得出答案.
【解答】解:∵A(3,0),B(0,4),
∴AO=3,BO=4,
∴AB==5,
∴AB=AB′=5,故OB′=8,
∴点B′的坐标是(8,0).
故选:B.
二.填空题
12.【分析】根据坐标平移规律即可求出答案.
【解答】解:由题意可知:A的横坐标+3,纵坐标﹣2,即可求出平移后的坐标,
∴平移后A的坐标为(1,﹣1)
故答案为:(1,﹣1)
13.【分析】直接利用实际距离的定义,结合A,B,C点的坐标,进而得出答案.
【解答】解:由题意可得:M到A,B,C的“实际距离”相等,则点M的坐标为(1,﹣2),此时M到A,B,C的实际距离都为5.21世纪教育网版权所有
故答案为:(1,﹣2).
14.【分析】由题意设=(x1,y1),=(x2,y2),∥,则x1?y2=x2?y1,由此列出方程即可解决问题.21教育网
【解答】解:由题意:∵=(2,3),=(4,m),且∥,
∴2m=12,
∴m=6,
故答案为6.
15.【分析】点P(﹣1,2)与关于直线x=1对称的点纵坐标不变,两点到x=1的距离相等,据此可得其横坐标.www-2-1-cnjy-com
【解答】解:点P(﹣1,2)关于直线x=1对称的点的坐标为(3,2),
故答案为:(3,2).
16.【分析】将正方形OABC沿着OB方向平移OB个单位,即将正方形OABC沿先向右平移1个单位,再向上平移1个单位,根据平移规律即可求出点C的对应点坐标.
【解答】解:∵在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),
∴OC=OA=2,C(0,2),
∵将正方形OABC沿着OB方向平移OB个单位,即将正方形OABC沿先向右平移1个单位,再向上平移1个单位,2-1-c-n-j-y
∴点C的对应点坐标是(1,3).
故答案为(1,3).
17.【分析】画出P1~P6,寻找规律后即可解决问题.
【解答】解:如图所示,P1(﹣2,0),P2(2,﹣4),P3(0,4),P4(﹣2,﹣2),P5(2,﹣2),P6(0,2),【出处:21教育名师】
发现6次一个循环,
∵2017÷6=336…1,
∴点P2017的坐标与P1的坐标相同,即P2017(﹣2,0),
故答案为(﹣2,0).
三.解答题
18.【分析】先利用两点间的距离计算出AB、BC、AC的长,则可计算出△ABC的面积,再利用勾股定理的逆定理得到△ABC为直角三角形,∠ABC=90°,然后根据三角形面积公式计算△ABC的面积.【版权所有:21教育】
【解答】解:∵A(0,2),B(4,0),C(6,4),
∴AB==2,BC==2,AC==2,
∴△ABC的周长=AB+BC+AC=2+2+2=4+2;
∵AB2+BC2=AC2,
∴△ABC为直角三角形,∠ABC=90°,
∴△ABC的面积=?2?2=10.
19.【分析】(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据点的坐标并结合图形解答即可;
(3)根据图形写出点E′的坐标,再根据关于原点对称的点的坐标特征解答.
【解答】解:(1)点A的坐标为(﹣2,0),点B的坐标为(0,﹣3),点D的坐标为(4,0),点F的坐标为(0,3);【来源:21cnj*y.co*m】
(2)点B与点C的纵坐标相等,线段BC平行于x轴;
(3)点E关于y轴的对称点的坐标为(﹣3,3),它与点C关于原点对称.
20.【分析】(1)根据x轴上点的纵坐标为0列方程求出m的值,再求解即可;
(2)根据纵坐标与横坐标的关系列方程求出m的值,再求解即可;
(3)根据平行于y轴的直线上的点的横坐标相同列方程求出m的值,再求解即可.
【解答】解:(1)∵点P(2m+4,m﹣1)在x轴上,
∴m﹣1=0,
解得m=1,
∴2m+4=2×1+4=6,
m﹣1=0,
所以,点P的坐标为(6,0);
(2)∵点P(2m+4,m﹣1)的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,
解得m=﹣8,
∴2m+4=2×(﹣8)+4=﹣12,
m﹣1=﹣8﹣1=﹣9,
∴点P的坐标为(﹣12,﹣9);
(3)∵点P(2m+4,m﹣1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2m+4=2,
解得m=﹣1,
∴m﹣1=﹣1﹣1=﹣2,
∴点P的坐标为(2,﹣2).
21.【分析】(1)根据+|b﹣6|=0,可以求得a、b的值,根据长方形的性质,可以求得点B的坐标;21教育名师原创作品
(2)根据题意点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动,可以得到当点P移动4秒时,点P的位置和点P的坐标;
(3)由题意可以得到符合要求的有两种情况,分别求出两种情况下点P移动的时间即可.
【解答】解:(1)∵a、b满足+|b﹣6|=0,
∴a﹣4=0,b﹣6=0,
解得a=4,b=6,
∴点B的坐标是(4,6),
故答案是:4,6,(4,6);
(2)∵点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动,
∴2×4=8,
∵OA=4,OC=6,
∴当点P移动4秒时,在线段CB上,离点C的距离是:8﹣6=2,
即当点P移动4秒时,此时点P在线段CB上,离点C的距离是2个单位长度,点P的坐标是(2,6);
(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况,
第一种情况,当点P在OC上时,
点P移动的时间是:5÷2=2.5秒,
第二种情况,当点P在BA上时.
点P移动的时间是:(6+4+1)÷2=5.5秒,
故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是2.5秒或5.5秒.
22.【分析】(1)根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答;
(2)根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答;
(3)根据平行于y轴的直线上的点的横坐标相等求解;
(4)根据第二四象限角平分线上的点的横坐标与纵坐标互为相反数解答.
【解答】解:(1)∵点A(a,﹣5),B(8,b)关于y轴对称,
∴a=﹣8,b=﹣5;
(2))∵点A(a,﹣5),B(8,b)关于x轴对称,
∴a=8,b=5;
(3)∵AB∥y轴,
∴a=8,b为不等于﹣5的实数;
(4)∵A,B两点在第二、第四象限的角平分线上,
∴a=5,b=﹣8.
23.【分析】(1)利用平面坐标系分别得出各点坐标进而得出答案;
(2)利用(1)中各点横纵坐标关系得出都关于原点对称,进而得出答案.
【解答】解:(1)如图所示:A(﹣4,1),M(4,﹣1);
B(﹣1,2),N(1,﹣2);
C(﹣3,4),Q(3,﹣4);
(2)由(1)得,三角形MNQ中的对应点R的坐标为:(3,﹣2).
24.【分析】(1)由A、B坐标得出AB=5,根据点C是点A关于点B的对称点知BC=AB=5,据此可得;【来源:21·世纪·教育·网】
(2)根据S△BCD=BC?AD=10且BC=5,可得AD=4,即可知OP=2,据此可得答案.
【解答】解:(1)∵点A(8,0),点B(3,0),
∴AB=5,
∵点C是点A关于点B的对称点,
∴BC=AB,
则点C的坐标为(﹣2,0);
(2)如图,
由题意知S△BCD=BC?AD=10,BC=5,
∴AD=4,
则OP=2,
∴点P的坐标为(0,2)或(0,﹣2).
25.【分析】(1)根据点的位置,直接写出点的坐标;
(2)根据(1)中发现的规律,两点的横坐标、纵坐标都互为相反数,即横坐标的和为0,纵坐标的和为0,列方程,求a、b的值.21cnjy.com
【解答】解:(1)由图象可知,点A(2,3),点D(﹣2,﹣3),点B(1,2),点E(﹣1,﹣2),点C(3,1),21*cnjy*com
点F(﹣3,﹣1);
对应点的坐标特征为:横坐标、纵坐标都互为相反数;
(2)由(1)可知,a+3+2a=0,4﹣b+2b﹣3=0,解得a=﹣1,b=﹣1.
26.【分析】【应用】:(1)根据若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|,代入数据即可得出结论;21*cnjy*com
(2)由CD∥y轴,可设点D的坐标为(1,m),根据CD=2即可得出|0﹣m|=2,解之即可得出结论;
【拓展】:(1)根据两点之间的折线距离公式,代入数据即可得出结论;
(2)根据两点之间的折线距离公式结合d(E,H)=3,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)由点Q在x轴上,可设点Q的坐标为(x,0),根据三角形的面积公式结合三角形OPQ的面积为3即可求出x的值,再利用两点之间的折线距离公式即可得出结论.
【解答】解:【应用】:
(1)AB的长度为|﹣1﹣2|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).
故答案为:(1,2)或(1,﹣2).
【拓展】:
(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.
故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|2﹣1|+|0﹣t|=3,解得:t=±2.
故答案为:2或﹣2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴|x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;
当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.
故答案为:4或8.
一.选择题
1.点P(1,﹣2)关于y轴对称的点的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(﹣2,1)
2.如图在正方形网格中,若A(1,1),B(2,0),则C点的坐标为( )
A.(﹣3,﹣2) B.(3,﹣2) C.(﹣2,﹣3) D.(2,﹣3)
3.如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(﹣1,1),(﹣3,1),(﹣1,﹣1).30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
A.Q′(2,3),R′(4,1) B.Q′(2,3),R′(2,1)
C.Q′(2,2),R′(4,1) D.Q′(3,3),R′(3,1)
4.已知点P(1﹣2m,m﹣1),则不论m取什么值,该P点必不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,点P(m﹣3,4﹣2m)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)
7.在平面直角坐标系中,点P(1,2)到原点的距离是( )
A.1 B. C. D.
8.已知点A(m,1)与点B(5,n)关于原点对称,则m和n的值为( )
A.m=5,n=﹣1 B.m=﹣5,n=1 C.m=﹣1,n=﹣5 D.m=﹣5,n=﹣1
9.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
A.(﹣2,1) B.(﹣1,1) C.(1,﹣2) D.(﹣1,﹣2)
10.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(﹣1,﹣1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,﹣1),则点B′的坐标为( )
A.(4,2) B.(5,2) C.(6,2) D.(5,3)
11.如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是( )
A.(5,0) B.(8,0) C.(0,5) D.(0,8)
二.填空题
12.在平面直角坐标系中有一点A(﹣2,1),将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为 .2·1·c·n·j·y
13.定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为 .
14.阅读材料:设=(x1,y1),=(x2,y2),如果∥,则x1?y2=x2?y1.根据该材料填空:已知=(2,3),=(4,m),且∥,则m= .
15.如图,在平面直角坐标系中,直线m经过(1,0)点,且垂直x轴,则点P(﹣1,2)关于直线m的对称点的坐标为 .
16.如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移OB个单位,则点C的对应点坐标为 .
17.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1),B(0,﹣2),C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,点P3绕点A旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为 .
三.解答题
18.如图,△ABC的三个顶点的坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
19.如图是一个平面直角坐标系,按要求完成下列各小题.
(1)写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标;
(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?
(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.
20.已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.
(1)点P在x轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
21.如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
22.已知点A(a,﹣5),B(8,b) 根据下列要求确定a,b的值
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB∥y轴
(4)A,B两点在第二、第四象限的角平分线上.
23.如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.
(1)请分别写出点A与点M,点B与点N,点C与点Q的坐标;
(2)已知点P是三角形ABC内一点,其坐标为(﹣3,2),利用上述对应点之间的关系,写出三角形MNQ中的对应点R的坐标.
24.如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.
(1)求点C的坐标;
(2)如果点P在y轴上,过点P作直线l∥x轴,点A关于直线l的对称点是点D,那么当△BCD的面积等于10时,求点P的坐标.
25.如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
26.问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;21·世纪*教育网
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
答案与解析
一.选择题
1.【分析】关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案.
【解答】解:P(1,﹣2)关于y轴对称的点的坐标是(﹣1,﹣2),
故选:C.
2.【分析】根据A(1,1),B(2,0),再结合图形即可确定出点C的坐标.
【解答】解:∵点A的坐标是:(1,1),
点B的坐标是:(2,0),
∴点C的坐标是:(3,﹣2).
故选B.
3.【分析】由点P(﹣1,1)到P′(4,3)知,编队需向右平移5个单位、向上平移2个单位,据此可得.www.21-cn-jy.com
【解答】解:由点P(﹣1,1)到P′(4,3)知,编队需向右平移5个单位、向上平移2个单位,
∴点Q(﹣3,1)的对应点Q′坐标为(2,3),点R(﹣1,﹣1)的对应点R′(4,1),
故选:A.
4.【分析】分横坐标是正数和负数两种情况求出m的值,再求出纵坐标的正负情况,然后根据各象限内点的坐标特征解答.
【解答】解:①1﹣2m>0时,m<,
m﹣1<0,
所以,点P在第四象限,一定不在第一象限;
②1﹣2m<0时,m>,
m﹣1既可以是正数,也可以是负数,
点P可以在第二、三象限,
综上所述,P点必不在第一象限.
故选A.
5.【分析】分点P的横坐标是正数和负数两种情况讨论求解.
【解答】解:①m﹣3>0,即m>3时,﹣2m<﹣6,
4﹣2m<﹣2,
所以,点P(m﹣3,4﹣2m)在第四象限,不可能在第一象限;
②m﹣3<0,即m<3时,﹣2m>﹣6,
4﹣2m>﹣2,
点P(m﹣3,4﹣2m)可以在第二或三象限,
综上所述,点P不可能在第一象限.
故选A.
6.【分析】由AC∥x轴,A(﹣2,2),根据坐标的定义可求得y值,根据线段BC最小,确定BC⊥AC,垂足为点C,进一步求得BC的最小值和点C的坐标.
【解答】解:依题意可得:
∵AC∥x,
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即
BC的最小值=5﹣2=3,
此时点C的坐标为(3,2),
故选D.
7.【分析】求出1与2的平方和的算术平方根即可.
【解答】解:点P(1,2)到原点的距离是=.
故选D.
8.【分析】根据关于原点对称,则两点的横、纵坐标都是互为相反数,可得答案.
【解答】解:点A(m,1)与点B(5,n)关于原点对称,得
m=﹣5,n=﹣1.
故选:D.
9.【分析】首先确定x轴、y轴的位置,然后根据轴对称图形的定义判断.
【解答】解:棋盘中心方子的位置用(﹣1,0)表示,则这点所在的横线是x轴,右下角方子的位置用(0,﹣1),则这点所在的纵线是y轴,则当放的位置是(﹣1,1)时构成轴对称图形.21·cn·jy·com
故选B.
10.【分析】根据A点的坐标及对应点的坐标可得线段AB向右平移4个单位,然后可得B′点的坐标.
【解答】解:∵A(﹣1,﹣1)平移后得到点A′的坐标为(3,﹣1),
∴向右平移4个单位,
∴B(1,2)的对应点坐标为(1+4,2),
即(5,2).
故选:B.
11.【分析】直接利用勾股定理得出AB的长,再利用旋转的性质得出OB′的长,进而得出答案.
【解答】解:∵A(3,0),B(0,4),
∴AO=3,BO=4,
∴AB==5,
∴AB=AB′=5,故OB′=8,
∴点B′的坐标是(8,0).
故选:B.
二.填空题
12.【分析】根据坐标平移规律即可求出答案.
【解答】解:由题意可知:A的横坐标+3,纵坐标﹣2,即可求出平移后的坐标,
∴平移后A的坐标为(1,﹣1)
故答案为:(1,﹣1)
13.【分析】直接利用实际距离的定义,结合A,B,C点的坐标,进而得出答案.
【解答】解:由题意可得:M到A,B,C的“实际距离”相等,则点M的坐标为(1,﹣2),此时M到A,B,C的实际距离都为5.21世纪教育网版权所有
故答案为:(1,﹣2).
14.【分析】由题意设=(x1,y1),=(x2,y2),∥,则x1?y2=x2?y1,由此列出方程即可解决问题.21教育网
【解答】解:由题意:∵=(2,3),=(4,m),且∥,
∴2m=12,
∴m=6,
故答案为6.
15.【分析】点P(﹣1,2)与关于直线x=1对称的点纵坐标不变,两点到x=1的距离相等,据此可得其横坐标.www-2-1-cnjy-com
【解答】解:点P(﹣1,2)关于直线x=1对称的点的坐标为(3,2),
故答案为:(3,2).
16.【分析】将正方形OABC沿着OB方向平移OB个单位,即将正方形OABC沿先向右平移1个单位,再向上平移1个单位,根据平移规律即可求出点C的对应点坐标.
【解答】解:∵在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),
∴OC=OA=2,C(0,2),
∵将正方形OABC沿着OB方向平移OB个单位,即将正方形OABC沿先向右平移1个单位,再向上平移1个单位,2-1-c-n-j-y
∴点C的对应点坐标是(1,3).
故答案为(1,3).
17.【分析】画出P1~P6,寻找规律后即可解决问题.
【解答】解:如图所示,P1(﹣2,0),P2(2,﹣4),P3(0,4),P4(﹣2,﹣2),P5(2,﹣2),P6(0,2),【出处:21教育名师】
发现6次一个循环,
∵2017÷6=336…1,
∴点P2017的坐标与P1的坐标相同,即P2017(﹣2,0),
故答案为(﹣2,0).
三.解答题
18.【分析】先利用两点间的距离计算出AB、BC、AC的长,则可计算出△ABC的面积,再利用勾股定理的逆定理得到△ABC为直角三角形,∠ABC=90°,然后根据三角形面积公式计算△ABC的面积.【版权所有:21教育】
【解答】解:∵A(0,2),B(4,0),C(6,4),
∴AB==2,BC==2,AC==2,
∴△ABC的周长=AB+BC+AC=2+2+2=4+2;
∵AB2+BC2=AC2,
∴△ABC为直角三角形,∠ABC=90°,
∴△ABC的面积=?2?2=10.
19.【分析】(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据点的坐标并结合图形解答即可;
(3)根据图形写出点E′的坐标,再根据关于原点对称的点的坐标特征解答.
【解答】解:(1)点A的坐标为(﹣2,0),点B的坐标为(0,﹣3),点D的坐标为(4,0),点F的坐标为(0,3);【来源:21cnj*y.co*m】
(2)点B与点C的纵坐标相等,线段BC平行于x轴;
(3)点E关于y轴的对称点的坐标为(﹣3,3),它与点C关于原点对称.
20.【分析】(1)根据x轴上点的纵坐标为0列方程求出m的值,再求解即可;
(2)根据纵坐标与横坐标的关系列方程求出m的值,再求解即可;
(3)根据平行于y轴的直线上的点的横坐标相同列方程求出m的值,再求解即可.
【解答】解:(1)∵点P(2m+4,m﹣1)在x轴上,
∴m﹣1=0,
解得m=1,
∴2m+4=2×1+4=6,
m﹣1=0,
所以,点P的坐标为(6,0);
(2)∵点P(2m+4,m﹣1)的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,
解得m=﹣8,
∴2m+4=2×(﹣8)+4=﹣12,
m﹣1=﹣8﹣1=﹣9,
∴点P的坐标为(﹣12,﹣9);
(3)∵点P(2m+4,m﹣1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2m+4=2,
解得m=﹣1,
∴m﹣1=﹣1﹣1=﹣2,
∴点P的坐标为(2,﹣2).
21.【分析】(1)根据+|b﹣6|=0,可以求得a、b的值,根据长方形的性质,可以求得点B的坐标;21教育名师原创作品
(2)根据题意点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动,可以得到当点P移动4秒时,点P的位置和点P的坐标;
(3)由题意可以得到符合要求的有两种情况,分别求出两种情况下点P移动的时间即可.
【解答】解:(1)∵a、b满足+|b﹣6|=0,
∴a﹣4=0,b﹣6=0,
解得a=4,b=6,
∴点B的坐标是(4,6),
故答案是:4,6,(4,6);
(2)∵点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动,
∴2×4=8,
∵OA=4,OC=6,
∴当点P移动4秒时,在线段CB上,离点C的距离是:8﹣6=2,
即当点P移动4秒时,此时点P在线段CB上,离点C的距离是2个单位长度,点P的坐标是(2,6);
(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况,
第一种情况,当点P在OC上时,
点P移动的时间是:5÷2=2.5秒,
第二种情况,当点P在BA上时.
点P移动的时间是:(6+4+1)÷2=5.5秒,
故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是2.5秒或5.5秒.
22.【分析】(1)根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答;
(2)根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答;
(3)根据平行于y轴的直线上的点的横坐标相等求解;
(4)根据第二四象限角平分线上的点的横坐标与纵坐标互为相反数解答.
【解答】解:(1)∵点A(a,﹣5),B(8,b)关于y轴对称,
∴a=﹣8,b=﹣5;
(2))∵点A(a,﹣5),B(8,b)关于x轴对称,
∴a=8,b=5;
(3)∵AB∥y轴,
∴a=8,b为不等于﹣5的实数;
(4)∵A,B两点在第二、第四象限的角平分线上,
∴a=5,b=﹣8.
23.【分析】(1)利用平面坐标系分别得出各点坐标进而得出答案;
(2)利用(1)中各点横纵坐标关系得出都关于原点对称,进而得出答案.
【解答】解:(1)如图所示:A(﹣4,1),M(4,﹣1);
B(﹣1,2),N(1,﹣2);
C(﹣3,4),Q(3,﹣4);
(2)由(1)得,三角形MNQ中的对应点R的坐标为:(3,﹣2).
24.【分析】(1)由A、B坐标得出AB=5,根据点C是点A关于点B的对称点知BC=AB=5,据此可得;【来源:21·世纪·教育·网】
(2)根据S△BCD=BC?AD=10且BC=5,可得AD=4,即可知OP=2,据此可得答案.
【解答】解:(1)∵点A(8,0),点B(3,0),
∴AB=5,
∵点C是点A关于点B的对称点,
∴BC=AB,
则点C的坐标为(﹣2,0);
(2)如图,
由题意知S△BCD=BC?AD=10,BC=5,
∴AD=4,
则OP=2,
∴点P的坐标为(0,2)或(0,﹣2).
25.【分析】(1)根据点的位置,直接写出点的坐标;
(2)根据(1)中发现的规律,两点的横坐标、纵坐标都互为相反数,即横坐标的和为0,纵坐标的和为0,列方程,求a、b的值.21cnjy.com
【解答】解:(1)由图象可知,点A(2,3),点D(﹣2,﹣3),点B(1,2),点E(﹣1,﹣2),点C(3,1),21*cnjy*com
点F(﹣3,﹣1);
对应点的坐标特征为:横坐标、纵坐标都互为相反数;
(2)由(1)可知,a+3+2a=0,4﹣b+2b﹣3=0,解得a=﹣1,b=﹣1.
26.【分析】【应用】:(1)根据若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|,代入数据即可得出结论;21*cnjy*com
(2)由CD∥y轴,可设点D的坐标为(1,m),根据CD=2即可得出|0﹣m|=2,解之即可得出结论;
【拓展】:(1)根据两点之间的折线距离公式,代入数据即可得出结论;
(2)根据两点之间的折线距离公式结合d(E,H)=3,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)由点Q在x轴上,可设点Q的坐标为(x,0),根据三角形的面积公式结合三角形OPQ的面积为3即可求出x的值,再利用两点之间的折线距离公式即可得出结论.
【解答】解:【应用】:
(1)AB的长度为|﹣1﹣2|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).
故答案为:(1,2)或(1,﹣2).
【拓展】:
(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.
故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|2﹣1|+|0﹣t|=3,解得:t=±2.
故答案为:2或﹣2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴|x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;
当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.
故答案为:4或8.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
