冀教版九年级数学上册第27章反比例函数单元测试(含答案)
文档属性
| 名称 | 冀教版九年级数学上册第27章反比例函数单元测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-16 00:00:00 | ||
图片预览




文档简介
第27章反比例函数单元测试
一、单选题(共10题;共30分)
1.下列函数中,当x>0时,y随x的增大而减小的是(
)
A、y=x
B、y=
C、y=-
D、y=x2
2.已知反比例函数y=2x,下列结论中,不正确的是(
)
A、图象必经过点(1,2)
B、在每个象限内,y随x的增大而减少
C、图象在第一、三象限内
D、若x>1,则y>2
3.已知y=m+1xm-2是反比例函数,则函数图象在( )
A、第一、三象限
B、第二、四象限
C、第一、二象限
D、第三、四象限
4.在直线运动中,当路程s(千米)一定时,速度v(千米/小时)关于时间t(小时)的函数关系式的大致图象是(
)
A、
B、
C、
D、
5.下列函数不是反比例函数的是( )
A.y=3x
B.y=12x
C.y=x﹣1
D.y=x2
6.下列关系式中:①y=2x;;③y=﹣;④y=5x+1;⑤y=x2﹣1;⑥y=;⑦xy=11,y是x的反比例函数的共有( )
A、4个
B、3个
C、2个
D、1个
7.如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=kx与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
A.125
B.2+1
C.52
D.22
8.一次函数y=x+m(m≠0)与反比例函数
y=mx
的图象在同一平面直角坐标系中是(
)
A.
B.
C.
D.
9.在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为(
)
A.
B.
C.
D.
10.已知一次函数y1=ax+c和反比例函数y2=
bx
的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是(
)
A.
B.
C.
D.
二、填空题(共8题;共24分)
11.已知一个矩形的面积是20cm2
,
那么这个矩形的长y(cm)与宽x(cm)之间的函数关系式为________ .
12.有m台完全相同的机器一起工作,需m小时完成一项工作,当由x台机器(x为不大于m的正整数)完成同一项工作时,所需的时间y与机器台数x的函数关系式是________.
13.某住宅小区要种植面积为500m2的矩形草坪,草坪长y(m)与宽x(m)之间的函数关系为________ .
14.在反比例函数y=2k-3x的图象所在的每个象限中,如果函数值y随自变量的x值增大而增大,那么常数k的取值范围是________
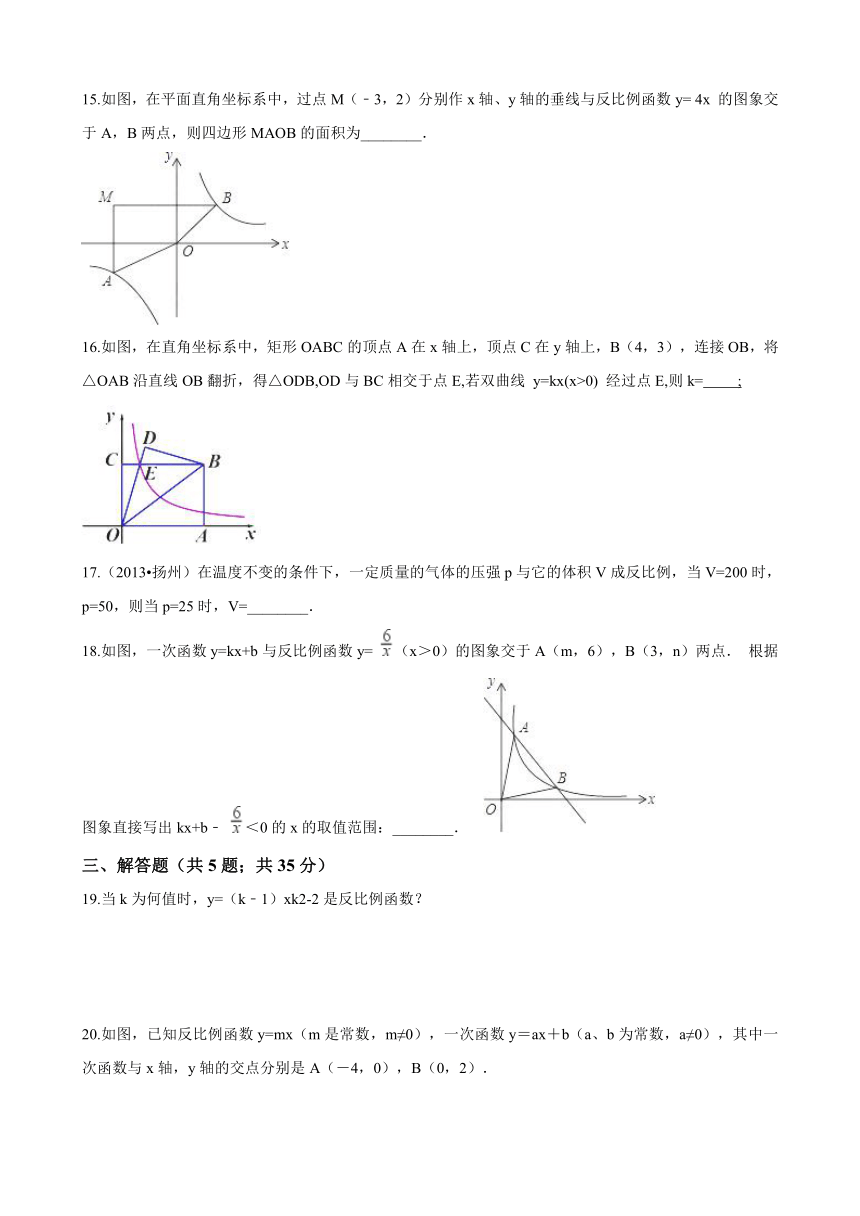
15.如图,在平面直角坐标系中,过点M(﹣3,2)分别作x轴、y轴的垂线与反比例函数y=
4x
的图象交于A,B两点,则四边形MAOB的面积为________.
16.如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线
y=kx(x>0)
经过点E,则k=
;
17.(2013 扬州)在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V=________.
18.如图,一次函数y=kx+b与反比例函数y=
(x>0)的图象交于A(m,6),B(3,n)两点.
根据图象直接写出kx+b﹣
<0的x的取值范围:________.
三、解答题(共5题;共35分)
19.当k为何值时,y=(k﹣1)xk2-2是反比例函数?
20.如图,已知反比例函数y=mx(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=17(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
21.如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数y=kx的图象经过格点A.
(1)请写出点A的坐标、反比例函数y=kx的解析式;
(2)若点B(m,y1)、C(n,y2)(2<m<n)都在函数y=kx的图象上,试比较y1与y2的大小.
22.某月食品加工厂以2万元引进一条新的生产加工线.已知加工这种食品的成本价每袋20元,物价部门规定:该食品的市场销售价不得高于每袋35元,若该食品的月销售量y(千袋)与销售单价x(元)之间的函数关系为:y=600x20(1)当销售单价定位25元时,该食品加工厂的月销量为多少千袋;
(2)求该加工厂的月获利M(千元)与销售单价x(元)之间的函数关系式;
(3)求销售单价范围在30<x≤35时,该加工厂是盈利还是亏损?若盈利,求出最大利润;若亏损,最小亏损是多少.
23.如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=kx图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及E点的坐标;
(2)求直线DE的解析式;
(3)若矩形OABC对角线的交点为F
(2,32),作FG⊥x轴交直线DE于点G.
①请判断点F是否在此反比例函数y=kx的图象上,并说明理由;
②求FG的长度.
四、综合题(共11分)
24.(在下列空格内填上正确或错误)
(1)如果y是x的反比例函数,那么当x增大时,y就减小________.
(2)当x与y乘积一定时,y就是x的反比例函数,x也是y的反比例函数________.
(3)如果一个函数不是正比例函数,就是反比例函数________.
(4)y与x2成反比例时y与x并不成反比例________.
(5)y与2x成反比例时,y与x也成反比例________.
(6)已知y与x成反比例,又知当x=2时,y=3,则y与x的函数关系式是y=
x6
________.
答案解析
一、单选题
1、【答案】B
【考点】正比例函数的图象和性质,反比例函数的性质,二次函数的性质
【解析】【分析】A、y=x,正比例函数,k>0,故y随着x的增大而增大;
B、y=(x>0),反比例函数,k>0,故在第一象限内y随x的增大而减小;
C、y=-(x>0),反比例函数,k<0,故在第四象限内y随x的增大而增大;
D、y=x2
,
故当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小.
【解答】A、∵k>0,∴y随着x的增大而增大;
B、∵k>0,∴在第一象限内y随x的增大而减小;
C、∵k<0,∴在第四象限内y随x的增大而增大;
D、∵y=x2
,
∴对称轴x=0,当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小.
故选B.
【点评】本题综合考查二次函数、反比例函数、正比例函数的增减性(单调性),是一道难度中等的题目.
2、【答案】D
【考点】反比例函数的性质
【解析】【分析】根据反比例函数图象上点的坐标特点:横纵坐标之积=k,可以判断出A的正误;根据反比例函数的性质:k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小可判断出B、C、D的正误.
【解答】A、反比例函数y=2x,所过的点的横纵坐标之积=2,此结论正确,故此选项不符合题意;
B、反比例函数y=2x,在每一象限内y随x的增大而减小,此结论正确,故此选项不符合题意;
C、反比例函数y=2x,图象在第一、三象限内,此结论正确,故此选项不合题意;
D、反比例函数y=2x,当x>1时图象在第四象限,y随x的增大而减小,故x>1,时y<2;
故选:D.
【点评】此题主要考查了反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是熟练掌握反比例函数的性质:
(1)反比例函数y=kx(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
3、【答案】A
【考点】反比例函数的图象,反比例函数的性质
【解析】【分析】先根据反比例函数的定义求得m的值,再根据反比例函数的性质判断结果。
【解答】由题意得m-2=-1,m=1,
则m+1=2>0,函数图象在第一、三象限,
故选A.
【点评】解答本题的关键是掌握当k>0时,反比例函数的图象在一、三象限,在每个象限内y随x的增大而减小;当k<0时,反比例函数的图象在二、四象限,在每个象限内y随x的增大而增大。
4、【答案】D
【考点】反比例函数的图象
【解析】【分析】根据速度公式v=St,由于S是定值,所以速度与时间是反比例函数关系;又由于某种原因时间和速度均不能为负数,根据反比例函数的性质,图象位于第一象限。
故选D.
5、【答案】D
【考点】反比例函数的定义
【解析】【解答】解:A、y=3x是反比例函数,与要求不符;
B、y=12x=12x是反比例函数,与要求不符;
C、y=x﹣1=1x是反比例函数,与要求不符;
D、y=x2是正比例函数,与要求相符.
故选:D.
【分析】根据反比例函数和正比例函数的定义回答即可.
6、【答案】C
【考点】反比例函数的定义
【解析】【解答】解:①y=2x是正比例函数;
可化为y=5x,是正比例函数;
③y=﹣符合反比例函数的定义,是反比例函数;
④y=5x+1是一次函数;
⑤y=x2﹣1是二次函数;
⑥y=不是函数;
⑦xy=11可化为y=,
符合反比例函数的定义,是反比例函数.
故选C.
【分析】分别根据反比例函数、二次函数及一次函数的定义对各小题进行逐一分析即可.
7、【答案】B
【考点】反比例函数系数k的几何意义
【解析】【解答】解:设D(t,kt),
∵矩形OGHF的面积为1,DF⊥x轴于点F,
∴HF=1t
,
而EG⊥y轴于点G,
∴E点的纵坐标为1t
,
当y=1t时,kx=1t
,
解得x=kt,
∴E(kt,1t),
∵矩形HDBE的面积为2,
∴(kt﹣t) (kt﹣1t)=2,
整理得(k﹣1)2=2,
而k>0,
∴k=2+1.
故选B.
【分析】设D(t,kt),由矩形OGHF的面积为1得到HF=1t
,
于是根据反比例函数图象上点的坐标特征可表示出E点坐标为(kt,1t),接着利用矩形面积公式得到(kt﹣t) (kt﹣1t)=2,然后解关于k的方程即可得到满足条件的k的值.
8、【答案】C
【考点】一次函数的图象,反比例函数的图象
【解析】【解答】解:A、对于反比例函数图象得到m<0,则对于y=x+m与y轴的交点在x轴下方,所以A选项不正确;
B、因为y=x+m中,k=1>0,所以其图象必过第一、三象限,所以B选项不正确;
C、对于反比例函数图象得到m<0,则对于y=x+m与y轴的交点在x轴下方,并且y=x+m的图象必过第一、三象限,所以C选项正确;
D、对于y=x+m,其图象必过第一、三象限,所以D选项不正确.
故选C.
【分析】根据一次函数的图象性质,y=x+m的图象必过第一、三象限,可对B、D进行判断;根据反比例函数的性质当m<0,y=x+m与y轴的交点在x轴下方,可对A、D进行判断.
9、【答案】B
【考点】反比例函数的图象,反比例函数的性质
【解析】【解答】解:∵DH垂直平分AC,
∴AD=CD=y,AH=CH=
12
AC=2,∠CHD=90°,
∵CD∥AB,
∴∠DCH=∠BAC,
∴△CDH∽△ACB,
∴
CDAC=CHAB
,
y4
=
2x
,
∴y=
8x
(0<x<4).
故选B.
【分析】先利用线段垂直平分线的性质得到AD=CD=y,AH=CH=
12
AC=2,∠CHD=90°,再证明△CDH∽△ACB,则利用相似比可得到y=
8x
(0<x<4),然后利用反比例函数的图象和自变量的取值范围对各选项进行判断.
10、【答案】B
【考点】一次函数的图象,反比例函数的图象
【解析】【解答】解:∵一次函数y1=ax+c图象过第一、二、四象限,
∴a<0,c>0,
∴二次函数y3=ax2+bx+c开口向下,与y轴交点在x轴上方;
∵反比例函数y2=
bx
的图象在第二、四象限,
∴b<0,
∴﹣
b2a
<0,
∴二次函数y3=ax2+bx+c对称轴在y轴左侧.
满足上述条件的函数图象只有B选项.
故选B.
【分析】根据一次函数与反比例函数图象找出a、b、c的正负,再根据抛物线的对称轴为x=﹣
b2a
,找出二次函数对称轴在y轴左侧,比对四个选项的函数图象即可得出结论.
二、填空题
11、【答案】y=20x
【考点】根据实际问题列反比例函数关系式
【解析】【解答】解:∵一个矩形的面积是20cm2
,
∴这个矩形的长y(cm)与宽x(cm)之间的函数关系式为:xy=20,即y=20x.
故答案为:y=20x.
【分析】利用矩形的面积公式得出xy=20,进而求出即可.
12、【答案】y=m2x
【考点】根据实际问题列反比例函数关系式
【解析】【解答】解:设每台机器1小时的工作效率为1.
m台完全相同的机器一起工作,需m小时完成一项工作,那么总工作量=m2
,
每台机器1小时的工作效率为1,x台机器1小时的工作效率为x.
∴y=m2x.
故答案为:y=m2x.
【分析】根据所需的时间=总工作量÷x台机器的工作效率,把相关数值代入即可求解.
13、【答案】y=5000x
【考点】根据实际问题列反比例函数关系式
【解析】【解答】解:由题意得:草坪长y(m)与宽x(m)之间的函数关系为y=5000x.
故本题答案为:y=5000x.
【分析】根据等量关系“矩形草坪长=矩形草坪面积÷矩形草坪宽”即可列出关系式.
14、【答案】k<32
【考点】反比例函数的性质
【解析】【解答】解:∵函数y=2k-3x的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,
∴2k﹣3<0,
解得k<32
.
故答案为:k<32
.
【分析】先根据函数y=2k-3x的图象在其所在的每一象限内,函数值y随自变量x的增大而增大列出关于m的不等式,求出m的取值范围即可.
15、【答案】10
【考点】反比例函数系数k的几何意义
【解析】【解答】解:如图,
设点A的坐标为(a,b),点B的坐标为(c,d),
∵反比例函数y=
4x
的图象过A,B两点,
∴ab=4,cd=4,
∴S△AOC=
12
|ab|=2,S△BOD=
12
|cd|=2,
∵点M(﹣3,2),
∴S矩形MCDO=3×2=6,
∴四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO=2+2+6=10,
故答案为:10.
【分析】设点A的坐标为(a,b),点B的坐标为(c,d),根据反比例函数y=
4x
的图象过A,B两点,所以ab=4,cd=4,进而得到S△AOC=
12
|ab|=2,S△BOD=
12
|cd|=2,
S矩形MCDO=3×2=6,根据四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO
,
即可解答.
16、【答案】218
【考点】反比例函数的性质
【解析】【解答】解:B点的坐标为(4,3),则OA=CB=4,OC=AB=3,
易知
Δ
OBD≌OBA,则∠D=∠OAB=90°,BD=OC=3.
四边形OABC是矩形,则∠OCB=90°,即∠OCB=∠D.
因为∠OEC=∠BED,所以
Δ
OEC≌
Δ
BED,CE=DE.
令CE=DE=x,则有:
CE+BE=x+
x2+33
=4,解得x=
78
.
E点的坐标为(
78
,3).
双曲线过点E,则k=
78
×3=
218
.
故答案为
218
.
【分析】双曲线过点E,关键是求出E点的坐标,已知B点的坐标是(4,3),显然E点和B点的纵坐标是相同的,即E点的纵坐标是3。
Δ
BOD由
Δ
OBA折叠而来,所以二者是全等的,进而可以证明
Δ
OEC≌
Δ
BED,CE=DE。从而求出CE的长度,即E点的横坐标。
17、【答案】400
【考点】反比例函数的应用
【解析】【解答】解:∵在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,
∴设P=
kv
∵当V=200时,p=50,
∴k=VP=200×50=10000,
∴P=
10000v
当P=25时,得v=
1000025
=400
故答案为:400.
【分析】首先利用待定系数法求得v与P的函数关系式,然后代入P求得v值即可.
18、【答案】0<x<1或x>3
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:把A、B的坐标代入反比例函数y=
得:m=1,n=2,
即A的坐标为(1,6),B的坐标为(3,2),
所以kx+b﹣
<0的x的取值范围为0<x<1或x>3,
故答案为:0<x<1或x>3.
【分析】先把A、B的坐标代入反比例函数的解析式,求出A、B的坐标,根据两点的坐标和图象得出即可.
三、解答题
19、【答案】【解答】解:y=(k﹣1)xk2-2是反比例函数,得:k2-2=-1k-1≠0,解得:k=﹣1,
当k=﹣1时,y=(k﹣1)xk2-2是反比例函数.
【考点】反比例函数的定义
【解析】【分析】根据反比例函数的定义,可得答案.
20、【答案】解:(1)∵一次函数y=ax+b与x轴,y轴的交点分别是A(﹣4,0),B(0,2),
∴-4a-b=0b=2,解得a=12b=2.
∴一次函数的关系式为:y=12x+2.
(2)设P(﹣4,p),则42+p2=17,解得:p
=±1.
由题意知p
=﹣1,p
=1舍去.
把P(﹣4,﹣1)代入反比例函数y=mx,得m=4.
∴反比例函数的关系式为:y=4x.
(3)∵P(﹣4,﹣1),∴关于原点的对称点Q的坐标为Q(4,1).
∵把Q(4,1)代入反比例函数关系式y=4x成立,
∴Q在该反比例函数的图象上.
【考点】待定系数法求一次函数解析式,待定系数法求反比例函数解析式,关于原点对称的点的坐标
【解析】【分析】(1)用待定系数法即可得出一次函数的解析式;
(2)先求出P点的坐标,然后用待定系数法即可求出反比例函数解析式;
(3)先求出P关于原点对称的点Q的坐标,然后代入反比例函数验证即可.
21、【答案】解:(1)由表得知A(﹣5,1),
∵反比例函数y=kx的图象经过格点A.
∴k=﹣5,
∴反比例函数y=kx的解析式为:y=﹣5x;
(2)∵k=﹣5<0,
∴在每个象限内,y随x的增大而增大,
∵2<m<n,
∴y1<y2
.
【考点】反比例函数的性质
【解析】【分析】(1)由图可得点A的坐标为:(﹣5,1),又由反比例函数y=kx经过A点,利用待定系数法即可求得反比例函数解析式;
(2)由反比例函数的性质:k<0时,在每个象限内,y随x的增大而增大,因为2<m<n,所以B,C都在第四象限,所以y1<y2
.
22、【答案】解:(1)当x=25时,y=60025=24千袋,
所以当销售单价定位25元时,该食品加工厂的月销量为24千袋;
(2)当20<x≤30时,M=600x(x﹣20)﹣20=580﹣12000x;
当30<x≤35时,M=(0.5x+10)(x﹣20)﹣20=12x2﹣220;
(3)当30<x≤35时,M=12x2﹣220,当x=35时,w最大,则w=12×352﹣220=392.5(千元)=39.25(万元),
答:此时该加工厂盈利,最大利润为:39.25万元.
【考点】一次函数的应用,反比例函数的应用
【解析】【分析】(1)将x=25代入反比例函数中求得y值即可确定月销量;
(2)用月销量×每袋的利润=总利润求得M(千元)与销售单价x(元)之间的函数关系式即可;
(3)求30<x≤35范围内的利润,利用二次函数增减性,即可确定最值.
23、【答案】解:(1)∵D
(1,3)在反比例函数y=kx 的图象上,
∴3=k1,
解得k=3
∴反比例函数的解析式为:y=3x,
∵B(4,3),
∴当x=4时,y=34,
∴E(4,34);
(2)设直线DE的解析式为y=kx+b(k≠0),
∵D(1,3),E(4,34),
∴k+b=34k+b=34,
解得k=-34b=154,
∴直线DE的解析式为:y=﹣34x+154;
(3)①点F在反比例函数的图象上.
理由如下:
∵当x=2时,y=3x=32
∴点F在反比例函数
y=3x的图象上.
②∵x=2时,y=﹣34x+154=94,
∴G点坐标为(2,94)
∴FG=94﹣32=34.
【考点】反比例函数的应用
【解析】【分析】(1)把点D(1,3)直接代入反比例函数的解析式即可得出k的值,进而得出反比例函数的解析式,再根据B(4,3)可知,直线AB的解析式x=4,再把x=4代入反比例函数关系式即可求出E点坐标;
(2)根据D、E两点的坐标用待定系数法求出直线DE的解析式;
(3)①直接把点F的坐标代入(1)中所求的反比例函数解析式进行检验即可;
②求出G点坐标,再求出FG的长度即可.
四、综合题
24、【答案】(1)错误
(2)错误
(3)错误
(4)正确
(5)正确
(6)错误
【考点】反比例函数的定义,反比例函数的性质,待定系数法求反比例函数解析式
【解析】【解答】解:(1)如果y是x的反比例函数,(当k>0时,在每个象限)当x增大时,y就减小.故答案为错误;(2)当x与y乘积一定时(不能为0),y就是x的反比例函数,x也是y的反比例函数.故答案为错误;(3)如果一个函数不是正比例函数,就是反比例函数.还有各种函数,如二次函数,故答案错误;(4)y与x2成反比例时,x2是自变量,y与x并不成反比例,故答案为正确;(5)y与2x成反比例时,设y=
k2x
,(k≠0),可转化为y=
12kx
,(
12
k≠0),所以y与x也成反比例,故答案为正确;(6)设y=
kx
,把x=2时,y=3代入解析式得,k=2×3=6,y与x的函数关系式是y=
6x
.故答案错误.
【分析】根据正比例函数与反比例函数的定义和性质及待定系数法解答.
一、单选题(共10题;共30分)
1.下列函数中,当x>0时,y随x的增大而减小的是(
)
A、y=x
B、y=
C、y=-
D、y=x2
2.已知反比例函数y=2x,下列结论中,不正确的是(
)
A、图象必经过点(1,2)
B、在每个象限内,y随x的增大而减少
C、图象在第一、三象限内
D、若x>1,则y>2
3.已知y=m+1xm-2是反比例函数,则函数图象在( )
A、第一、三象限
B、第二、四象限
C、第一、二象限
D、第三、四象限
4.在直线运动中,当路程s(千米)一定时,速度v(千米/小时)关于时间t(小时)的函数关系式的大致图象是(
)
A、
B、
C、
D、
5.下列函数不是反比例函数的是( )
A.y=3x
B.y=12x
C.y=x﹣1
D.y=x2
6.下列关系式中:①y=2x;;③y=﹣;④y=5x+1;⑤y=x2﹣1;⑥y=;⑦xy=11,y是x的反比例函数的共有( )
A、4个
B、3个
C、2个
D、1个
7.如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=kx与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
A.125
B.2+1
C.52
D.22
8.一次函数y=x+m(m≠0)与反比例函数
y=mx
的图象在同一平面直角坐标系中是(
)
A.
B.
C.
D.
9.在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为(
)
A.
B.
C.
D.
10.已知一次函数y1=ax+c和反比例函数y2=
bx
的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是(
)
A.
B.
C.
D.
二、填空题(共8题;共24分)
11.已知一个矩形的面积是20cm2
,
那么这个矩形的长y(cm)与宽x(cm)之间的函数关系式为________ .
12.有m台完全相同的机器一起工作,需m小时完成一项工作,当由x台机器(x为不大于m的正整数)完成同一项工作时,所需的时间y与机器台数x的函数关系式是________.
13.某住宅小区要种植面积为500m2的矩形草坪,草坪长y(m)与宽x(m)之间的函数关系为________ .
14.在反比例函数y=2k-3x的图象所在的每个象限中,如果函数值y随自变量的x值增大而增大,那么常数k的取值范围是________
15.如图,在平面直角坐标系中,过点M(﹣3,2)分别作x轴、y轴的垂线与反比例函数y=
4x
的图象交于A,B两点,则四边形MAOB的面积为________.
16.如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线
y=kx(x>0)
经过点E,则k=
;
17.(2013 扬州)在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V=________.
18.如图,一次函数y=kx+b与反比例函数y=
(x>0)的图象交于A(m,6),B(3,n)两点.
根据图象直接写出kx+b﹣
<0的x的取值范围:________.
三、解答题(共5题;共35分)
19.当k为何值时,y=(k﹣1)xk2-2是反比例函数?
20.如图,已知反比例函数y=mx(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=17(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
21.如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数y=kx的图象经过格点A.
(1)请写出点A的坐标、反比例函数y=kx的解析式;
(2)若点B(m,y1)、C(n,y2)(2<m<n)都在函数y=kx的图象上,试比较y1与y2的大小.
22.某月食品加工厂以2万元引进一条新的生产加工线.已知加工这种食品的成本价每袋20元,物价部门规定:该食品的市场销售价不得高于每袋35元,若该食品的月销售量y(千袋)与销售单价x(元)之间的函数关系为:y=600x20
(2)求该加工厂的月获利M(千元)与销售单价x(元)之间的函数关系式;
(3)求销售单价范围在30<x≤35时,该加工厂是盈利还是亏损?若盈利,求出最大利润;若亏损,最小亏损是多少.
23.如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=kx图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及E点的坐标;
(2)求直线DE的解析式;
(3)若矩形OABC对角线的交点为F
(2,32),作FG⊥x轴交直线DE于点G.
①请判断点F是否在此反比例函数y=kx的图象上,并说明理由;
②求FG的长度.
四、综合题(共11分)
24.(在下列空格内填上正确或错误)
(1)如果y是x的反比例函数,那么当x增大时,y就减小________.
(2)当x与y乘积一定时,y就是x的反比例函数,x也是y的反比例函数________.
(3)如果一个函数不是正比例函数,就是反比例函数________.
(4)y与x2成反比例时y与x并不成反比例________.
(5)y与2x成反比例时,y与x也成反比例________.
(6)已知y与x成反比例,又知当x=2时,y=3,则y与x的函数关系式是y=
x6
________.
答案解析
一、单选题
1、【答案】B
【考点】正比例函数的图象和性质,反比例函数的性质,二次函数的性质
【解析】【分析】A、y=x,正比例函数,k>0,故y随着x的增大而增大;
B、y=(x>0),反比例函数,k>0,故在第一象限内y随x的增大而减小;
C、y=-(x>0),反比例函数,k<0,故在第四象限内y随x的增大而增大;
D、y=x2
,
故当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小.
【解答】A、∵k>0,∴y随着x的增大而增大;
B、∵k>0,∴在第一象限内y随x的增大而减小;
C、∵k<0,∴在第四象限内y随x的增大而增大;
D、∵y=x2
,
∴对称轴x=0,当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小.
故选B.
【点评】本题综合考查二次函数、反比例函数、正比例函数的增减性(单调性),是一道难度中等的题目.
2、【答案】D
【考点】反比例函数的性质
【解析】【分析】根据反比例函数图象上点的坐标特点:横纵坐标之积=k,可以判断出A的正误;根据反比例函数的性质:k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小可判断出B、C、D的正误.
【解答】A、反比例函数y=2x,所过的点的横纵坐标之积=2,此结论正确,故此选项不符合题意;
B、反比例函数y=2x,在每一象限内y随x的增大而减小,此结论正确,故此选项不符合题意;
C、反比例函数y=2x,图象在第一、三象限内,此结论正确,故此选项不合题意;
D、反比例函数y=2x,当x>1时图象在第四象限,y随x的增大而减小,故x>1,时y<2;
故选:D.
【点评】此题主要考查了反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是熟练掌握反比例函数的性质:
(1)反比例函数y=kx(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
3、【答案】A
【考点】反比例函数的图象,反比例函数的性质
【解析】【分析】先根据反比例函数的定义求得m的值,再根据反比例函数的性质判断结果。
【解答】由题意得m-2=-1,m=1,
则m+1=2>0,函数图象在第一、三象限,
故选A.
【点评】解答本题的关键是掌握当k>0时,反比例函数的图象在一、三象限,在每个象限内y随x的增大而减小;当k<0时,反比例函数的图象在二、四象限,在每个象限内y随x的增大而增大。
4、【答案】D
【考点】反比例函数的图象
【解析】【分析】根据速度公式v=St,由于S是定值,所以速度与时间是反比例函数关系;又由于某种原因时间和速度均不能为负数,根据反比例函数的性质,图象位于第一象限。
故选D.
5、【答案】D
【考点】反比例函数的定义
【解析】【解答】解:A、y=3x是反比例函数,与要求不符;
B、y=12x=12x是反比例函数,与要求不符;
C、y=x﹣1=1x是反比例函数,与要求不符;
D、y=x2是正比例函数,与要求相符.
故选:D.
【分析】根据反比例函数和正比例函数的定义回答即可.
6、【答案】C
【考点】反比例函数的定义
【解析】【解答】解:①y=2x是正比例函数;
可化为y=5x,是正比例函数;
③y=﹣符合反比例函数的定义,是反比例函数;
④y=5x+1是一次函数;
⑤y=x2﹣1是二次函数;
⑥y=不是函数;
⑦xy=11可化为y=,
符合反比例函数的定义,是反比例函数.
故选C.
【分析】分别根据反比例函数、二次函数及一次函数的定义对各小题进行逐一分析即可.
7、【答案】B
【考点】反比例函数系数k的几何意义
【解析】【解答】解:设D(t,kt),
∵矩形OGHF的面积为1,DF⊥x轴于点F,
∴HF=1t
,
而EG⊥y轴于点G,
∴E点的纵坐标为1t
,
当y=1t时,kx=1t
,
解得x=kt,
∴E(kt,1t),
∵矩形HDBE的面积为2,
∴(kt﹣t) (kt﹣1t)=2,
整理得(k﹣1)2=2,
而k>0,
∴k=2+1.
故选B.
【分析】设D(t,kt),由矩形OGHF的面积为1得到HF=1t
,
于是根据反比例函数图象上点的坐标特征可表示出E点坐标为(kt,1t),接着利用矩形面积公式得到(kt﹣t) (kt﹣1t)=2,然后解关于k的方程即可得到满足条件的k的值.
8、【答案】C
【考点】一次函数的图象,反比例函数的图象
【解析】【解答】解:A、对于反比例函数图象得到m<0,则对于y=x+m与y轴的交点在x轴下方,所以A选项不正确;
B、因为y=x+m中,k=1>0,所以其图象必过第一、三象限,所以B选项不正确;
C、对于反比例函数图象得到m<0,则对于y=x+m与y轴的交点在x轴下方,并且y=x+m的图象必过第一、三象限,所以C选项正确;
D、对于y=x+m,其图象必过第一、三象限,所以D选项不正确.
故选C.
【分析】根据一次函数的图象性质,y=x+m的图象必过第一、三象限,可对B、D进行判断;根据反比例函数的性质当m<0,y=x+m与y轴的交点在x轴下方,可对A、D进行判断.
9、【答案】B
【考点】反比例函数的图象,反比例函数的性质
【解析】【解答】解:∵DH垂直平分AC,
∴AD=CD=y,AH=CH=
12
AC=2,∠CHD=90°,
∵CD∥AB,
∴∠DCH=∠BAC,
∴△CDH∽△ACB,
∴
CDAC=CHAB
,
y4
=
2x
,
∴y=
8x
(0<x<4).
故选B.
【分析】先利用线段垂直平分线的性质得到AD=CD=y,AH=CH=
12
AC=2,∠CHD=90°,再证明△CDH∽△ACB,则利用相似比可得到y=
8x
(0<x<4),然后利用反比例函数的图象和自变量的取值范围对各选项进行判断.
10、【答案】B
【考点】一次函数的图象,反比例函数的图象
【解析】【解答】解:∵一次函数y1=ax+c图象过第一、二、四象限,
∴a<0,c>0,
∴二次函数y3=ax2+bx+c开口向下,与y轴交点在x轴上方;
∵反比例函数y2=
bx
的图象在第二、四象限,
∴b<0,
∴﹣
b2a
<0,
∴二次函数y3=ax2+bx+c对称轴在y轴左侧.
满足上述条件的函数图象只有B选项.
故选B.
【分析】根据一次函数与反比例函数图象找出a、b、c的正负,再根据抛物线的对称轴为x=﹣
b2a
,找出二次函数对称轴在y轴左侧,比对四个选项的函数图象即可得出结论.
二、填空题
11、【答案】y=20x
【考点】根据实际问题列反比例函数关系式
【解析】【解答】解:∵一个矩形的面积是20cm2
,
∴这个矩形的长y(cm)与宽x(cm)之间的函数关系式为:xy=20,即y=20x.
故答案为:y=20x.
【分析】利用矩形的面积公式得出xy=20,进而求出即可.
12、【答案】y=m2x
【考点】根据实际问题列反比例函数关系式
【解析】【解答】解:设每台机器1小时的工作效率为1.
m台完全相同的机器一起工作,需m小时完成一项工作,那么总工作量=m2
,
每台机器1小时的工作效率为1,x台机器1小时的工作效率为x.
∴y=m2x.
故答案为:y=m2x.
【分析】根据所需的时间=总工作量÷x台机器的工作效率,把相关数值代入即可求解.
13、【答案】y=5000x
【考点】根据实际问题列反比例函数关系式
【解析】【解答】解:由题意得:草坪长y(m)与宽x(m)之间的函数关系为y=5000x.
故本题答案为:y=5000x.
【分析】根据等量关系“矩形草坪长=矩形草坪面积÷矩形草坪宽”即可列出关系式.
14、【答案】k<32
【考点】反比例函数的性质
【解析】【解答】解:∵函数y=2k-3x的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,
∴2k﹣3<0,
解得k<32
.
故答案为:k<32
.
【分析】先根据函数y=2k-3x的图象在其所在的每一象限内,函数值y随自变量x的增大而增大列出关于m的不等式,求出m的取值范围即可.
15、【答案】10
【考点】反比例函数系数k的几何意义
【解析】【解答】解:如图,
设点A的坐标为(a,b),点B的坐标为(c,d),
∵反比例函数y=
4x
的图象过A,B两点,
∴ab=4,cd=4,
∴S△AOC=
12
|ab|=2,S△BOD=
12
|cd|=2,
∵点M(﹣3,2),
∴S矩形MCDO=3×2=6,
∴四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO=2+2+6=10,
故答案为:10.
【分析】设点A的坐标为(a,b),点B的坐标为(c,d),根据反比例函数y=
4x
的图象过A,B两点,所以ab=4,cd=4,进而得到S△AOC=
12
|ab|=2,S△BOD=
12
|cd|=2,
S矩形MCDO=3×2=6,根据四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO
,
即可解答.
16、【答案】218
【考点】反比例函数的性质
【解析】【解答】解:B点的坐标为(4,3),则OA=CB=4,OC=AB=3,
易知
Δ
OBD≌OBA,则∠D=∠OAB=90°,BD=OC=3.
四边形OABC是矩形,则∠OCB=90°,即∠OCB=∠D.
因为∠OEC=∠BED,所以
Δ
OEC≌
Δ
BED,CE=DE.
令CE=DE=x,则有:
CE+BE=x+
x2+33
=4,解得x=
78
.
E点的坐标为(
78
,3).
双曲线过点E,则k=
78
×3=
218
.
故答案为
218
.
【分析】双曲线过点E,关键是求出E点的坐标,已知B点的坐标是(4,3),显然E点和B点的纵坐标是相同的,即E点的纵坐标是3。
Δ
BOD由
Δ
OBA折叠而来,所以二者是全等的,进而可以证明
Δ
OEC≌
Δ
BED,CE=DE。从而求出CE的长度,即E点的横坐标。
17、【答案】400
【考点】反比例函数的应用
【解析】【解答】解:∵在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,
∴设P=
kv
∵当V=200时,p=50,
∴k=VP=200×50=10000,
∴P=
10000v
当P=25时,得v=
1000025
=400
故答案为:400.
【分析】首先利用待定系数法求得v与P的函数关系式,然后代入P求得v值即可.
18、【答案】0<x<1或x>3
【考点】反比例函数与一次函数的交点问题
【解析】【解答】解:把A、B的坐标代入反比例函数y=
得:m=1,n=2,
即A的坐标为(1,6),B的坐标为(3,2),
所以kx+b﹣
<0的x的取值范围为0<x<1或x>3,
故答案为:0<x<1或x>3.
【分析】先把A、B的坐标代入反比例函数的解析式,求出A、B的坐标,根据两点的坐标和图象得出即可.
三、解答题
19、【答案】【解答】解:y=(k﹣1)xk2-2是反比例函数,得:k2-2=-1k-1≠0,解得:k=﹣1,
当k=﹣1时,y=(k﹣1)xk2-2是反比例函数.
【考点】反比例函数的定义
【解析】【分析】根据反比例函数的定义,可得答案.
20、【答案】解:(1)∵一次函数y=ax+b与x轴,y轴的交点分别是A(﹣4,0),B(0,2),
∴-4a-b=0b=2,解得a=12b=2.
∴一次函数的关系式为:y=12x+2.
(2)设P(﹣4,p),则42+p2=17,解得:p
=±1.
由题意知p
=﹣1,p
=1舍去.
把P(﹣4,﹣1)代入反比例函数y=mx,得m=4.
∴反比例函数的关系式为:y=4x.
(3)∵P(﹣4,﹣1),∴关于原点的对称点Q的坐标为Q(4,1).
∵把Q(4,1)代入反比例函数关系式y=4x成立,
∴Q在该反比例函数的图象上.
【考点】待定系数法求一次函数解析式,待定系数法求反比例函数解析式,关于原点对称的点的坐标
【解析】【分析】(1)用待定系数法即可得出一次函数的解析式;
(2)先求出P点的坐标,然后用待定系数法即可求出反比例函数解析式;
(3)先求出P关于原点对称的点Q的坐标,然后代入反比例函数验证即可.
21、【答案】解:(1)由表得知A(﹣5,1),
∵反比例函数y=kx的图象经过格点A.
∴k=﹣5,
∴反比例函数y=kx的解析式为:y=﹣5x;
(2)∵k=﹣5<0,
∴在每个象限内,y随x的增大而增大,
∵2<m<n,
∴y1<y2
.
【考点】反比例函数的性质
【解析】【分析】(1)由图可得点A的坐标为:(﹣5,1),又由反比例函数y=kx经过A点,利用待定系数法即可求得反比例函数解析式;
(2)由反比例函数的性质:k<0时,在每个象限内,y随x的增大而增大,因为2<m<n,所以B,C都在第四象限,所以y1<y2
.
22、【答案】解:(1)当x=25时,y=60025=24千袋,
所以当销售单价定位25元时,该食品加工厂的月销量为24千袋;
(2)当20<x≤30时,M=600x(x﹣20)﹣20=580﹣12000x;
当30<x≤35时,M=(0.5x+10)(x﹣20)﹣20=12x2﹣220;
(3)当30<x≤35时,M=12x2﹣220,当x=35时,w最大,则w=12×352﹣220=392.5(千元)=39.25(万元),
答:此时该加工厂盈利,最大利润为:39.25万元.
【考点】一次函数的应用,反比例函数的应用
【解析】【分析】(1)将x=25代入反比例函数中求得y值即可确定月销量;
(2)用月销量×每袋的利润=总利润求得M(千元)与销售单价x(元)之间的函数关系式即可;
(3)求30<x≤35范围内的利润,利用二次函数增减性,即可确定最值.
23、【答案】解:(1)∵D
(1,3)在反比例函数y=kx 的图象上,
∴3=k1,
解得k=3
∴反比例函数的解析式为:y=3x,
∵B(4,3),
∴当x=4时,y=34,
∴E(4,34);
(2)设直线DE的解析式为y=kx+b(k≠0),
∵D(1,3),E(4,34),
∴k+b=34k+b=34,
解得k=-34b=154,
∴直线DE的解析式为:y=﹣34x+154;
(3)①点F在反比例函数的图象上.
理由如下:
∵当x=2时,y=3x=32
∴点F在反比例函数
y=3x的图象上.
②∵x=2时,y=﹣34x+154=94,
∴G点坐标为(2,94)
∴FG=94﹣32=34.
【考点】反比例函数的应用
【解析】【分析】(1)把点D(1,3)直接代入反比例函数的解析式即可得出k的值,进而得出反比例函数的解析式,再根据B(4,3)可知,直线AB的解析式x=4,再把x=4代入反比例函数关系式即可求出E点坐标;
(2)根据D、E两点的坐标用待定系数法求出直线DE的解析式;
(3)①直接把点F的坐标代入(1)中所求的反比例函数解析式进行检验即可;
②求出G点坐标,再求出FG的长度即可.
四、综合题
24、【答案】(1)错误
(2)错误
(3)错误
(4)正确
(5)正确
(6)错误
【考点】反比例函数的定义,反比例函数的性质,待定系数法求反比例函数解析式
【解析】【解答】解:(1)如果y是x的反比例函数,(当k>0时,在每个象限)当x增大时,y就减小.故答案为错误;(2)当x与y乘积一定时(不能为0),y就是x的反比例函数,x也是y的反比例函数.故答案为错误;(3)如果一个函数不是正比例函数,就是反比例函数.还有各种函数,如二次函数,故答案错误;(4)y与x2成反比例时,x2是自变量,y与x并不成反比例,故答案为正确;(5)y与2x成反比例时,设y=
k2x
,(k≠0),可转化为y=
12kx
,(
12
k≠0),所以y与x也成反比例,故答案为正确;(6)设y=
kx
,把x=2时,y=3代入解析式得,k=2×3=6,y与x的函数关系式是y=
6x
.故答案错误.
【分析】根据正比例函数与反比例函数的定义和性质及待定系数法解答.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
