13.4 课题学习 最短路径问题同步练习(解析版)
文档属性
| 名称 | 13.4 课题学习 最短路径问题同步练习(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 510.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-17 07:40:13 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
新人教版八年级数学上册同步练习
13.4课题学习 最短路径问题
一、单选题
1.如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
21·世纪*教育网
A、转化思想 B、三角形的两边之和大于第三边
C、两点之间,线段最短 D、三角形的一个外角大于与它不相邻的任意一个内角
2.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )21·cn·jy·com
A、135° B、130° C、125° D、120°
3.已知直线l同旁的两点A、B,在l上求一点P,使PA+PB最小,则求P点的作法正确的为( )
A、作A关于l的对称点A′,连接A′B交l与P B、AB的延长线与l交于P
C、作A关于l的对称点A′,连接AA′交l与P D、以上都不对
4.如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A、 B、3 C、4 D、2
5.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
21世纪教育网版权所有
A.6 B.8 C.10 D.12
6.如图,在△ABC中,∠ACB=90°,以AC为一边在△ABC外侧作等边三角形ACD,过点D作DE⊥AC,垂足为F,DE与AB相交于点E,连接CE,AB=15cm,BC=9cm,P是射线DE上的一点.连接PC、PB,若△PBC的周长最小,则最小值为( )
21*cnjy*com
A、22cm B、21cm C、24 cm D、27cm
7.如图,在锐角三角形ABC中,AC=6,△ABC的面积为15,∠BAC的平分线交BC与点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
A、4 B、5 C、6 D、7
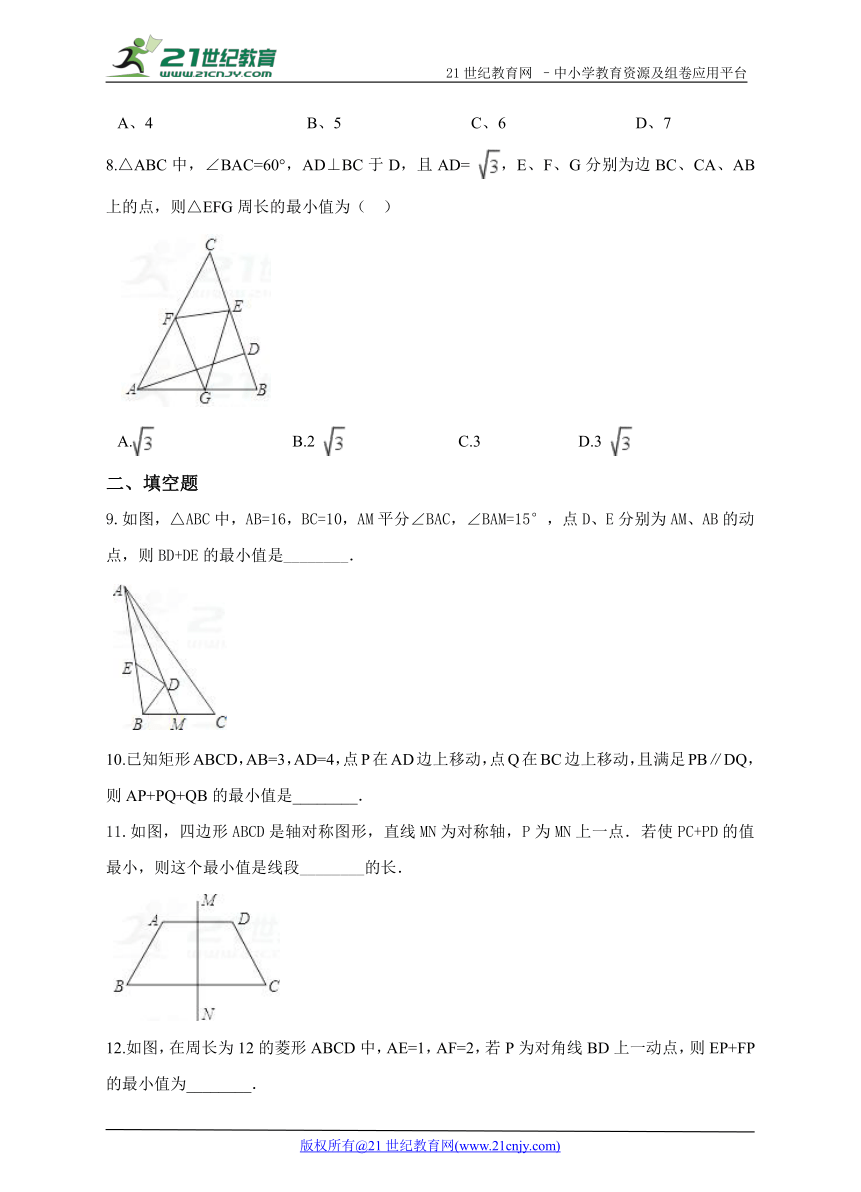
8.△ABC中,∠BAC=60°,AD⊥BC于D,且AD= ,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
A. B.2 C.3 D.3
二、填空题
9.如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是________.【来源:21·世纪·教育·网】
10.已知矩形ABCD,AB=3,AD=4,点P在AD边上移动,点Q在BC边上移动,且满足PB∥DQ,则AP+PQ+QB的最小值是________.
11.如图,四边形ABCD是轴对称图形,直线MN为对称轴,P为MN上一点.若使PC+PD的值最小,则这个最小值是线段________的长.
12.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为________.2·1·c·n·j·y
13.如图,线段AB与线段CD关于直线L对称,点P是直线L上一动点,测得:点D与点A之间的距离为8cm,点B与点D之间的距离为5cm,那么PA+PB的最小值是________.
14.如图,△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F、E分别为AC、AD上两动点,连接CE、EF,则CE+EF的最小值为________.
三、作图题
15.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
16.作图题:(不写作法,但要保留痕迹)
如图1,已知点C、D和∠AOB,求作一点P,使P到点C、D的距离相等,且到∠AOB的两边的距离相等.在图2中直线m上找到一点Q,使它到A、B两点的距离和最小.
17.如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为akm和bkm,且张、李二村庄相距ckm.
水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置.
21教育网
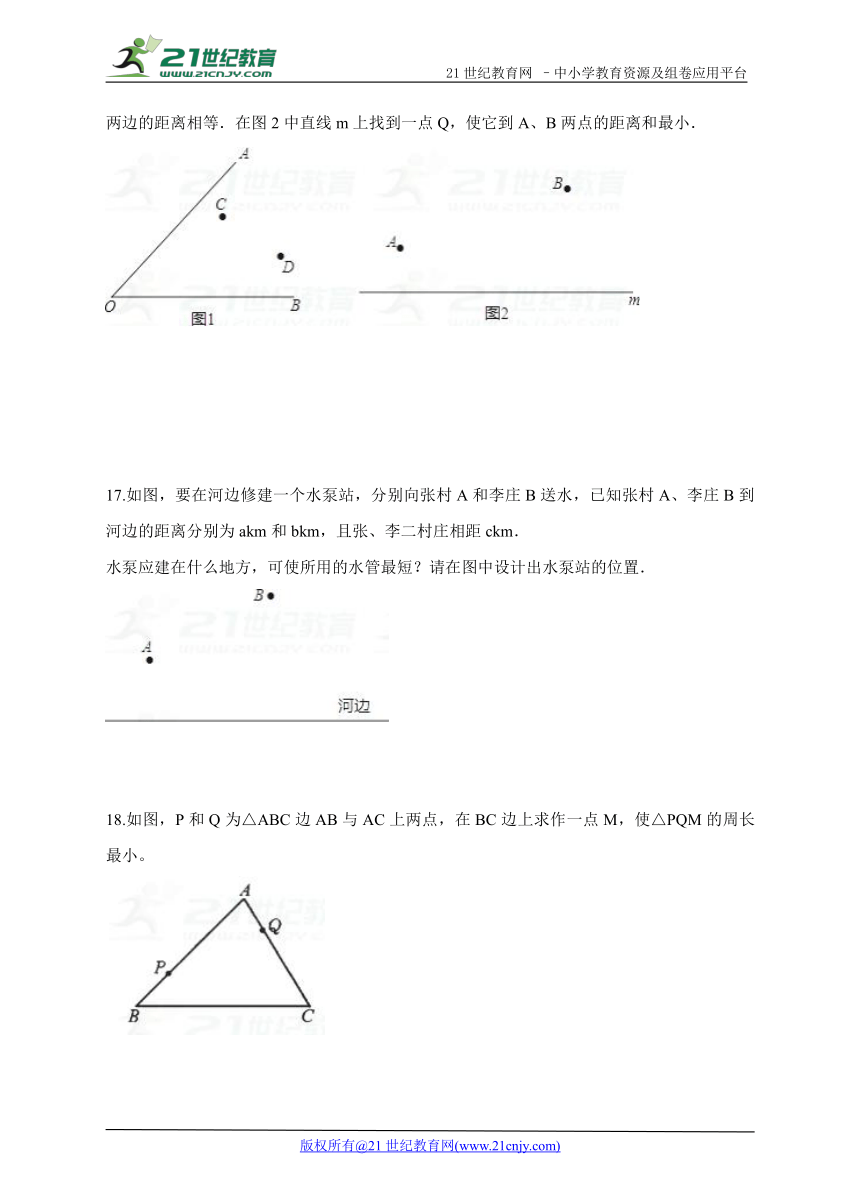
18.如图,P和Q为△ABC边AB与AC上两点,在BC边上求作一点M,使△PQM的周长最小。
21cnjy.com
参考答案与试题解析
一、单选题
1、D
解:∵点B和点B′关于直线l对称,且点C在l上,
∴CB=CB′,
又∵AB′交l与C,且两条直线相交只有一个交点,
∴CB′+CA最短,
即CA+CB的值最小,
将轴对称最短路径问题利用线段的性质定理两点之间,线段最短,体现了转化思想,验证时利用三角形的两边之和大于第三边.
故选D.www.21-cn-jy.com
2、D解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值. ∵∠DAB=120°,
∴∠AA′M+∠A″=180°﹣120°=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
故选:D.2-1-c-n-j-y
3、A
解:作法:①作A关于l的对称点A′,则PA+PB=PA′+PB, ②连接A′B交l与P,
则P就是所求作的点;
根据两点之间,线段最短,可知:此时PA+PB最小;
故选A.【来源:21cnj*y.co*m】
4、D
解:连接BD,与AC交于点F.
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为4,
∴AB=2.
又∵△ABE是等边三角形,
∴BE=AB=2.
∴所求最小值为2.
故选:D.【出处:21教育名师】
5、C
解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= 12 BC AD= 12 ×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+ 12 BC=8+ 12 ×4=8+2=10.
故选C.
【版权所有:21教育】
6、C
解:根据轴对称求最短路径的知识,可得当点P与点E重合的时候PB+PC最小,也即△PBC的周长最小,此时PB=PC= AB= cm,
故△PBC的最小周长=PB+PC+BC=AB+BC=15+9=24cm.
故选C.21教育名师原创作品
7、B
解:如图,作N关于AD的对称点N′,连接MN′,作BN″⊥AC于N″交AD于M′.
∵BM+MN=BM+MN′≤BN″,
∴当M与M′,N与N″重合时,BN″最小,
∵ ×AC×BN″=15,AC=6,
∴BN″=5,
∴BM+MN的最小值为5,
故选B.www-2-1-cnjy-com
8、C
解:在BC上任取一点E,连接AE, 把△ABE沿AB翻折得△ABE′,把△ACE沿AC翻折得△ACE″,
∵∠BAC=60°,
∴∠E′AE″=120°,AE=AE′=AE″,
连接E′E″交AB、AC于G、F.连接GE,EF,
∵GE=E′G,EF=E″F,
∴△GEF的周长=GE+GF+EF=E′G+GF+E″F=E′E″= AE,
∵根据垂线段最短可知AD⊥BC时AD的值最小,
∴当点E与点D重合时,AE最小,
∴△DEF的周长的最小值= × =3.
故选C.
二、填空题
9、8
解:作BF⊥AC于点F,如右图所示, ∵在△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,∠BFA=90°,
∴∠BAC=30°,
∴AB=2BF,
∴BF=8,
∵AM平分∠BAC,点D、E分别为AM、AB的动点,F
∴BD+DE的最小值是BF,
∴BD+DE=8,
故答案为:8.
10、7
解:∵平行四边形ABCD中,AD∥BC, 又∵PB∥DQ,
∴四边形PDBQ是平行四边形,
∴QB=PD,
∴AP+PQ+QB=AP+PD+PQ=AD+PQ,
当PQ于BC垂直时AD+PQ=AD+AB=7最小.
故答案为:7.
11、AC或BD解:∵四边形ABCD是轴对称图形,直线MN为对称轴, ∴点A与点D关于直线MN对称,
∴连接AC(BD),则线段AC或BD的长即为PC+PD的最小值.
故答案为:AC或BD.
12、3
解:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P. ∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故答案为:3.
13、8cm
解:∵线段AB与线段CD关于直线L对称,
∴点B与点D关于直线L对称,
连接AD,交于直线L于点P,则此时PA+PB最小,且PB=PD,
∴PA+PB=PA+PD=AD=8cm.
故答案为:8cm.
14、6
解:作F关于AD的对称点为M,作AB边上的高CP,
∵AD平分∠CAB,△ABC为锐角三角形,
∴M必在AC上,
∵F关于AD的对称点为M,
∴ME=EF,
∴EF+EC=EM+EC,
即EM+EC=MC≥PC(垂线段最短),
∵△ABC的面积是30,AB=10,
∴ 12 ×10×PC=30,
∴PC=6,
即CE+EF的最小值为:6.
故答案为:6.
三、作图题
15、解:作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
16、解:如图1,点P即为所求;
如图2,点Q即为所求.
17、解:如图所示:
18、解:如图,作点P关于BC的对称点P′,连接P′Q,交BC于点M,点M是所求的点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
新人教版八年级数学上册同步练习
13.4课题学习 最短路径问题
一、单选题
1.如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
21·世纪*教育网
A、转化思想 B、三角形的两边之和大于第三边
C、两点之间,线段最短 D、三角形的一个外角大于与它不相邻的任意一个内角
2.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )21·cn·jy·com
A、135° B、130° C、125° D、120°
3.已知直线l同旁的两点A、B,在l上求一点P,使PA+PB最小,则求P点的作法正确的为( )
A、作A关于l的对称点A′,连接A′B交l与P B、AB的延长线与l交于P
C、作A关于l的对称点A′,连接AA′交l与P D、以上都不对
4.如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A、 B、3 C、4 D、2
5.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
21世纪教育网版权所有
A.6 B.8 C.10 D.12
6.如图,在△ABC中,∠ACB=90°,以AC为一边在△ABC外侧作等边三角形ACD,过点D作DE⊥AC,垂足为F,DE与AB相交于点E,连接CE,AB=15cm,BC=9cm,P是射线DE上的一点.连接PC、PB,若△PBC的周长最小,则最小值为( )
21*cnjy*com
A、22cm B、21cm C、24 cm D、27cm
7.如图,在锐角三角形ABC中,AC=6,△ABC的面积为15,∠BAC的平分线交BC与点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
A、4 B、5 C、6 D、7
8.△ABC中,∠BAC=60°,AD⊥BC于D,且AD= ,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
A. B.2 C.3 D.3
二、填空题
9.如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是________.【来源:21·世纪·教育·网】
10.已知矩形ABCD,AB=3,AD=4,点P在AD边上移动,点Q在BC边上移动,且满足PB∥DQ,则AP+PQ+QB的最小值是________.
11.如图,四边形ABCD是轴对称图形,直线MN为对称轴,P为MN上一点.若使PC+PD的值最小,则这个最小值是线段________的长.
12.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为________.2·1·c·n·j·y
13.如图,线段AB与线段CD关于直线L对称,点P是直线L上一动点,测得:点D与点A之间的距离为8cm,点B与点D之间的距离为5cm,那么PA+PB的最小值是________.
14.如图,△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F、E分别为AC、AD上两动点,连接CE、EF,则CE+EF的最小值为________.
三、作图题
15.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
16.作图题:(不写作法,但要保留痕迹)
如图1,已知点C、D和∠AOB,求作一点P,使P到点C、D的距离相等,且到∠AOB的两边的距离相等.在图2中直线m上找到一点Q,使它到A、B两点的距离和最小.
17.如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为akm和bkm,且张、李二村庄相距ckm.
水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置.
21教育网
18.如图,P和Q为△ABC边AB与AC上两点,在BC边上求作一点M,使△PQM的周长最小。
21cnjy.com
参考答案与试题解析
一、单选题
1、D
解:∵点B和点B′关于直线l对称,且点C在l上,
∴CB=CB′,
又∵AB′交l与C,且两条直线相交只有一个交点,
∴CB′+CA最短,
即CA+CB的值最小,
将轴对称最短路径问题利用线段的性质定理两点之间,线段最短,体现了转化思想,验证时利用三角形的两边之和大于第三边.
故选D.www.21-cn-jy.com
2、D解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值. ∵∠DAB=120°,
∴∠AA′M+∠A″=180°﹣120°=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
故选:D.2-1-c-n-j-y
3、A
解:作法:①作A关于l的对称点A′,则PA+PB=PA′+PB, ②连接A′B交l与P,
则P就是所求作的点;
根据两点之间,线段最短,可知:此时PA+PB最小;
故选A.【来源:21cnj*y.co*m】
4、D
解:连接BD,与AC交于点F.
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为4,
∴AB=2.
又∵△ABE是等边三角形,
∴BE=AB=2.
∴所求最小值为2.
故选:D.【出处:21教育名师】
5、C
解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= 12 BC AD= 12 ×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+ 12 BC=8+ 12 ×4=8+2=10.
故选C.
【版权所有:21教育】
6、C
解:根据轴对称求最短路径的知识,可得当点P与点E重合的时候PB+PC最小,也即△PBC的周长最小,此时PB=PC= AB= cm,
故△PBC的最小周长=PB+PC+BC=AB+BC=15+9=24cm.
故选C.21教育名师原创作品
7、B
解:如图,作N关于AD的对称点N′,连接MN′,作BN″⊥AC于N″交AD于M′.
∵BM+MN=BM+MN′≤BN″,
∴当M与M′,N与N″重合时,BN″最小,
∵ ×AC×BN″=15,AC=6,
∴BN″=5,
∴BM+MN的最小值为5,
故选B.www-2-1-cnjy-com
8、C
解:在BC上任取一点E,连接AE, 把△ABE沿AB翻折得△ABE′,把△ACE沿AC翻折得△ACE″,
∵∠BAC=60°,
∴∠E′AE″=120°,AE=AE′=AE″,
连接E′E″交AB、AC于G、F.连接GE,EF,
∵GE=E′G,EF=E″F,
∴△GEF的周长=GE+GF+EF=E′G+GF+E″F=E′E″= AE,
∵根据垂线段最短可知AD⊥BC时AD的值最小,
∴当点E与点D重合时,AE最小,
∴△DEF的周长的最小值= × =3.
故选C.
二、填空题
9、8
解:作BF⊥AC于点F,如右图所示, ∵在△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,∠BFA=90°,
∴∠BAC=30°,
∴AB=2BF,
∴BF=8,
∵AM平分∠BAC,点D、E分别为AM、AB的动点,F
∴BD+DE的最小值是BF,
∴BD+DE=8,
故答案为:8.
10、7
解:∵平行四边形ABCD中,AD∥BC, 又∵PB∥DQ,
∴四边形PDBQ是平行四边形,
∴QB=PD,
∴AP+PQ+QB=AP+PD+PQ=AD+PQ,
当PQ于BC垂直时AD+PQ=AD+AB=7最小.
故答案为:7.
11、AC或BD解:∵四边形ABCD是轴对称图形,直线MN为对称轴, ∴点A与点D关于直线MN对称,
∴连接AC(BD),则线段AC或BD的长即为PC+PD的最小值.
故答案为:AC或BD.
12、3
解:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P. ∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故答案为:3.
13、8cm
解:∵线段AB与线段CD关于直线L对称,
∴点B与点D关于直线L对称,
连接AD,交于直线L于点P,则此时PA+PB最小,且PB=PD,
∴PA+PB=PA+PD=AD=8cm.
故答案为:8cm.
14、6
解:作F关于AD的对称点为M,作AB边上的高CP,
∵AD平分∠CAB,△ABC为锐角三角形,
∴M必在AC上,
∵F关于AD的对称点为M,
∴ME=EF,
∴EF+EC=EM+EC,
即EM+EC=MC≥PC(垂线段最短),
∵△ABC的面积是30,AB=10,
∴ 12 ×10×PC=30,
∴PC=6,
即CE+EF的最小值为:6.
故答案为:6.
三、作图题
15、解:作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
16、解:如图1,点P即为所求;
如图2,点Q即为所求.
17、解:如图所示:
18、解:如图,作点P关于BC的对称点P′,连接P′Q,交BC于点M,点M是所求的点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
