12.3角的平分线的性质课件(1)(共17张PPT)
文档属性
| 名称 | 12.3角的平分线的性质课件(1)(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 771.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-17 00:00:00 | ||
图片预览


文档简介
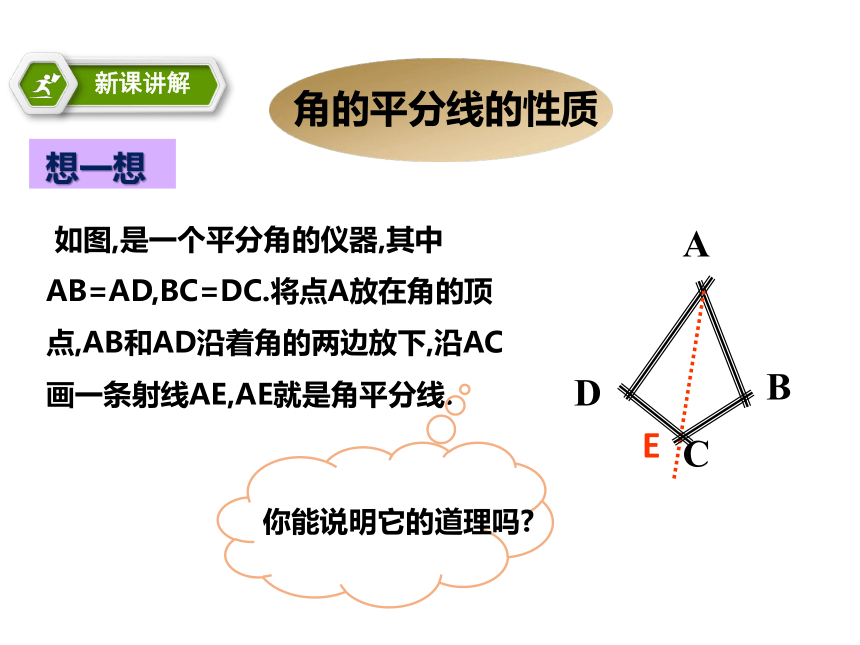
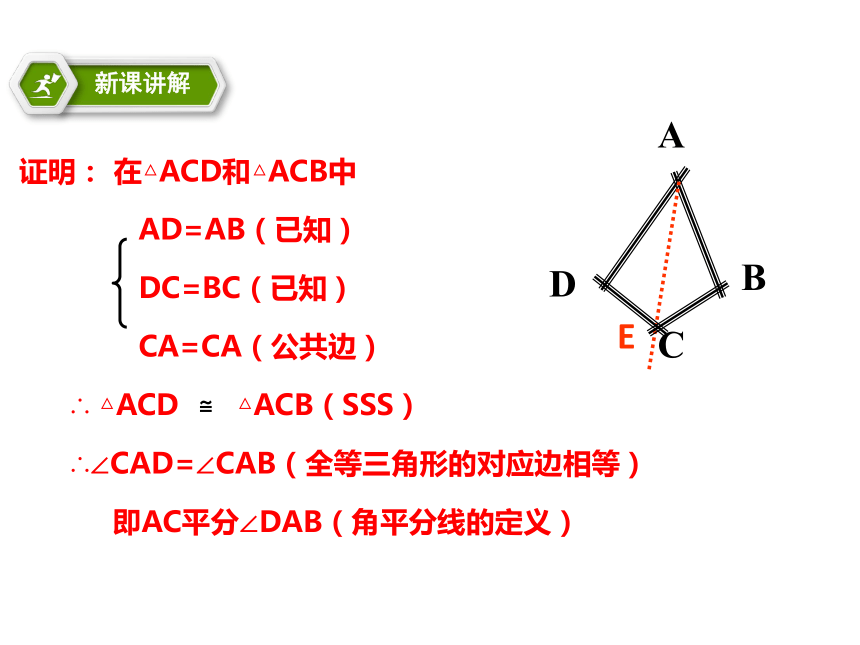
课件17张PPT。12.3 角的平分线的性质一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。什么是角平分线?如图OC即为∠AOB的平分线。角平分线具有哪些性质呢?角的平分线的性质想一想 如图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.E你能说明它的道理吗?E证明: 在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的对应边相等)
即AC平分∠DAB(角平分线的定义)
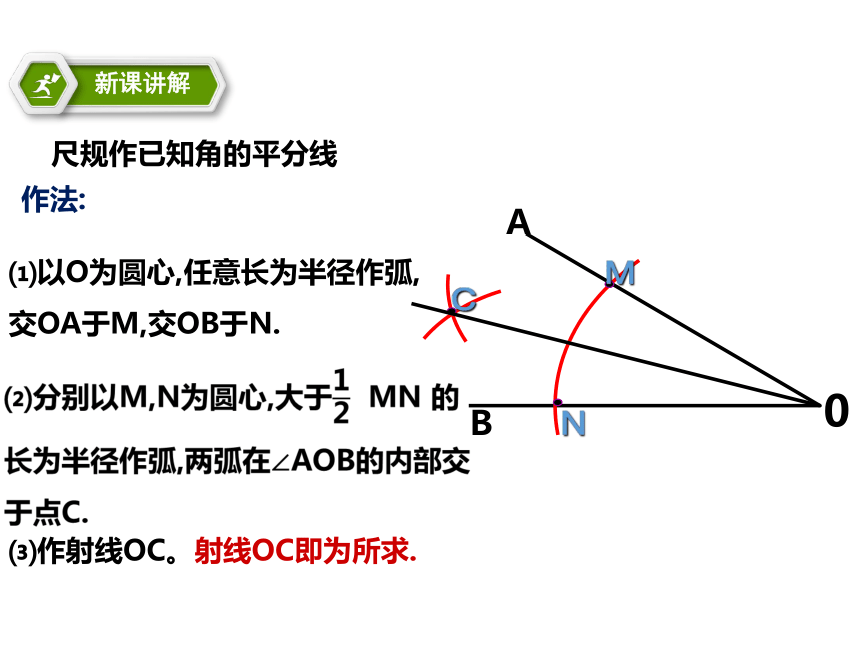
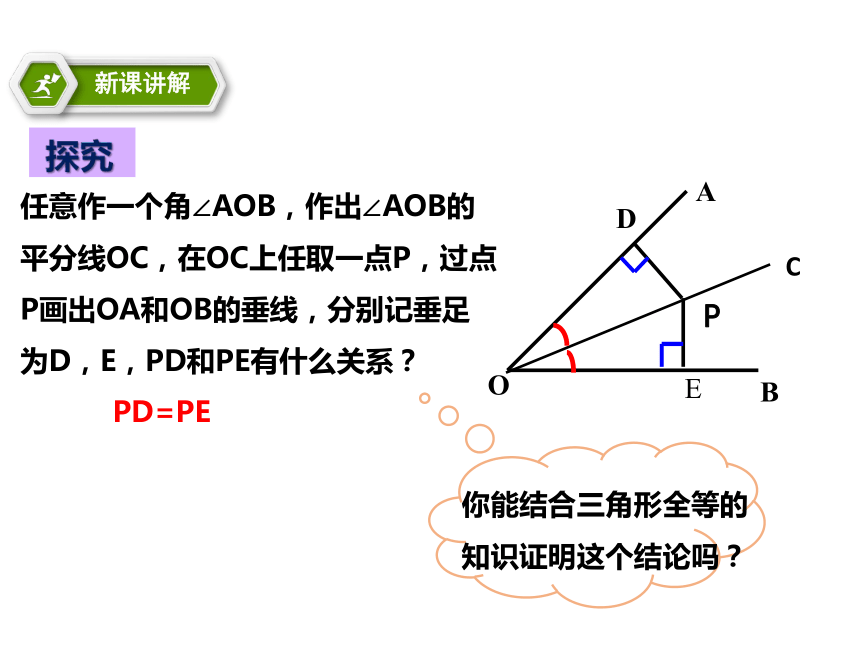
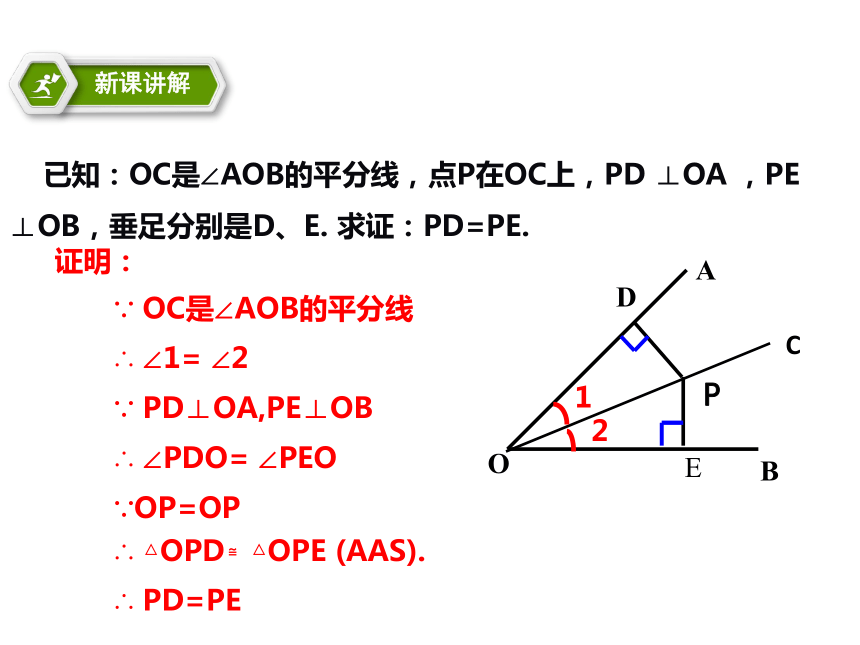
≌?AB⑶作射线OC。射线OC即为所求.0尺规作已知角的平分线作法:⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.探究任意作一个角∠AOB,作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA和OB的垂线,分别记垂足为D,E,PD和PE有什么关系?PD=PE你能结合三角形全等的知识证明这个结论吗? 已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E. 求证:PD=PE.证明:
∵ OC是∠AOB的平分线
∴ ∠1= ∠2
∵ PD⊥OA,PE⊥OB
∴ ∠PDO= ∠PEO
∵OP=OP
∴ △OPD △OPE (AAS).
∴ PD=PE
12≌探究再在OC上任取一点Q、R,过点Q、R画出OA和OB的垂线,分别记垂足为F、H和J、K,QE与QH、RJ与RK分别有什么关系?QF=QH你能总结出角的平分线的性质吗?RJ=RKQRJFHK角的平分线的性质:角平分线上的点到角的两边的距离相等。PD ⊥OA ,PE ⊥OB∵OP平分∠AOB∴PD=PE.用符号表示为:定理应用所具备的条件:定理的作用: 证明线段相等。证明几何命题的一般步骤:
1、明确命题的已知和求证;
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是多少?∵BD是∠ABC的平分线,∠C=90°,DE⊥AB,
∴DE=CD,
∵CD=3cm,
∴DE=3cm.ACBDE证明:过D作DE⊥AB于E,利用角平分线性质的必备条件,缺一不可1.如图,△ABC中,∠C=90°,AC=BC,AD是∠CAB的平分线,DE⊥AB于E.已知AC=6cm,则BD+DE的和为( )
A. 5cm B. 6cm C. 7cm D. 8cmB2.如图,△ABC中,∠C=90°,AC=BC,AD是∠CAB的平分线,DE⊥AB于E.已知AB=10cm,则△BDE的周长为 。10cm∵BM是△ABC的角平分线,点P在BM上,∴PD=PE.同理,PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等.证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等。PMN结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等. 2.如图,OC是∠AOB的角平分线,P是OC上点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.证明:∵OC是∠AOB的角平分线,PD⊥OA,PE⊥OB,
∴PD=PE.∠PDO=∠PEO=90°.
在Rt△PDO和Rt△PEO中,
PO=PO
PD=PE,
∴Rt△PDO Rt△PEO(HL),∴OD=OE,∠POD=∠POE.
在△DOF和△EOF中,
OD=OE
∠POD=∠POE
PO=PO, ∴△DOF △EOF(SAS),∴DF=EF.≌≌角的平分线的性质:角平分线上的点到角的两边的距离相等。PD ⊥OA ,PE ⊥OB∵OP平分∠AOB∴PD=PE.用符号表示为:小结:这节课我们学了哪些知识?添哪些辅助线?
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的对应边相等)
即AC平分∠DAB(角平分线的定义)
≌?AB⑶作射线OC。射线OC即为所求.0尺规作已知角的平分线作法:⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.探究任意作一个角∠AOB,作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA和OB的垂线,分别记垂足为D,E,PD和PE有什么关系?PD=PE你能结合三角形全等的知识证明这个结论吗? 已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E. 求证:PD=PE.证明:
∵ OC是∠AOB的平分线
∴ ∠1= ∠2
∵ PD⊥OA,PE⊥OB
∴ ∠PDO= ∠PEO
∵OP=OP
∴ △OPD △OPE (AAS).
∴ PD=PE
12≌探究再在OC上任取一点Q、R,过点Q、R画出OA和OB的垂线,分别记垂足为F、H和J、K,QE与QH、RJ与RK分别有什么关系?QF=QH你能总结出角的平分线的性质吗?RJ=RKQRJFHK角的平分线的性质:角平分线上的点到角的两边的距离相等。PD ⊥OA ,PE ⊥OB∵OP平分∠AOB∴PD=PE.用符号表示为:定理应用所具备的条件:定理的作用: 证明线段相等。证明几何命题的一般步骤:
1、明确命题的已知和求证;
2、根据题意,画出图形,并用数学符号表示已知和求证;
3、经过分析,找出由已知推出求证的途径,写出证明过程。如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是多少?∵BD是∠ABC的平分线,∠C=90°,DE⊥AB,
∴DE=CD,
∵CD=3cm,
∴DE=3cm.ACBDE证明:过D作DE⊥AB于E,利用角平分线性质的必备条件,缺一不可1.如图,△ABC中,∠C=90°,AC=BC,AD是∠CAB的平分线,DE⊥AB于E.已知AC=6cm,则BD+DE的和为( )
A. 5cm B. 6cm C. 7cm D. 8cmB2.如图,△ABC中,∠C=90°,AC=BC,AD是∠CAB的平分线,DE⊥AB于E.已知AB=10cm,则△BDE的周长为 。10cm∵BM是△ABC的角平分线,点P在BM上,∴PD=PE.同理,PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等.证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等。PMN结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等. 2.如图,OC是∠AOB的角平分线,P是OC上点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.证明:∵OC是∠AOB的角平分线,PD⊥OA,PE⊥OB,
∴PD=PE.∠PDO=∠PEO=90°.
在Rt△PDO和Rt△PEO中,
PO=PO
PD=PE,
∴Rt△PDO Rt△PEO(HL),∴OD=OE,∠POD=∠POE.
在△DOF和△EOF中,
OD=OE
∠POD=∠POE
PO=PO, ∴△DOF △EOF(SAS),∴DF=EF.≌≌角的平分线的性质:角平分线上的点到角的两边的距离相等。PD ⊥OA ,PE ⊥OB∵OP平分∠AOB∴PD=PE.用符号表示为:小结:这节课我们学了哪些知识?添哪些辅助线?
