第三章 位置与坐标单元检测题B

北师版数学八年级上册第3章《位置与坐标》单元检测题B
一．选择题
1．在x轴上，且到原点的距离为2的点的坐标是（　　）
A．（2，0） B．（﹣2，0） C．（2，0）或（﹣2，0） D．（0，2）
2．已知点P（x+3，x﹣4）在x轴上，则x的值为（　　）
A．3 B．﹣3 C．﹣4 D．4
3．若点A（a﹣2，3）和点B（﹣1，b+5）关于y轴对称，则点C（a，b）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．中国象棋是中华民族的文化瑰宝，它渊远流长，趣味浓厚．如图，在某平面直角坐标系中，所在位置的坐标为（﹣3，1），所在位置的坐标为（2，﹣1），那么，所在位置的坐标为（　　）
A．（0，1） B．（4，0） C．（﹣1，0） D．（0，﹣1）
5．若点P（m，2）与点Q（3，n）关于原点对称，则m，n的值分别为（　　）
A．﹣3，2 B．3，﹣2 C．﹣3，﹣2 D．3，2
6．坐标平面上，在第二象限内有一点P，且P点到x轴的距离是4，到y轴的距离是5，则P点的坐标为（　　）
A．（﹣5，4） B．（﹣4，5） C．（4，5） D．（5，﹣4）
7．已知点（a，a）a≠0，给出下列变换：
①关于x轴轴对称；
②关于直线y=﹣x轴对称；
③关于原点中心对称．
其中通过变换能得到坐标为（﹣a，﹣a）的变换是（　　）
A．①② B．②③ C．③ D．①③
8．如图，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是（　　）
A．先向左平移5个单位，再向下平移2个单位
B．先向右平移5个单位，再向下平移2个单位
C．先向左平移5个单位，再向上平移2个单位
D．先向右平移5个单位，再向上平移2个单位
9．如图，平面直角坐标系中，A、B两点的坐标分别为（2，0）、（0，1），若将线段AB平移至A1B1，则a，b的值分别为（　　）
A．1，3 B．1，2 C．2，1 D．1，1
10．如图，正方形OABC在平面直角坐标系中，点A的坐标为（2，0），将正方形OABC绕点O顺时针旋转45°，得到正方形OA′B′C′，则点C′的坐标为（　　）
A．（，） B．（﹣，） C．（，） D．（2，2）
11．如图，在平面直角坐标系中，将△ABO绕点A顺指针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…，若点A（，0），B（0，4），则点B2016的横坐标为（　　）
A．5 B．12 C．10070 D．10080
12．如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到，则点P的坐标为（　　）
A．（0，1） B．（0，﹣1） C．（1，﹣1） D．（1，0）
二．填空题
13．已知点A在x轴上方，到x轴的距离是3，到y轴的距离是4，那么点A的坐标是　 　．
14．已知P1（a﹣1，5）和P2（2，b﹣1）关于x轴对称，则（a+b）2017的值为　 　．
15．如图，把△ABC经过一定的变换得到△A′B′C′，如果图中△ABC上的点P的坐标为（a，b），那么它的对应点P′的坐标为　 　．
16．在平面直角坐标系中，△A′B′C′是由△ABC平移后得到的，△ABC中任意一点P（x0，y0）经过平移后对应点为P′（x0+7，y0+2），若A′的坐标为（5，3），则它的对应的点A的坐标为　 　．
17．如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P（1，2）在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置…，则正方形铁片连续旋转2017次后，点P的坐标为　 　．
18．如图，已知△ABC三个顶点的坐标分别为A（0，4），B（﹣1，1），C（﹣2，2），将△ABC向右平移4个单位，得到△A′B′C′，点A，B，C的对应点分别为A′、B′、C′，再将△A′B′C′绕点B′顺时针旋转90°，得到△A″B″C″，点A′、B′、C′的对应点分别为A″、B″、C″，则点A″的坐标为　 　．
　
三．解答题
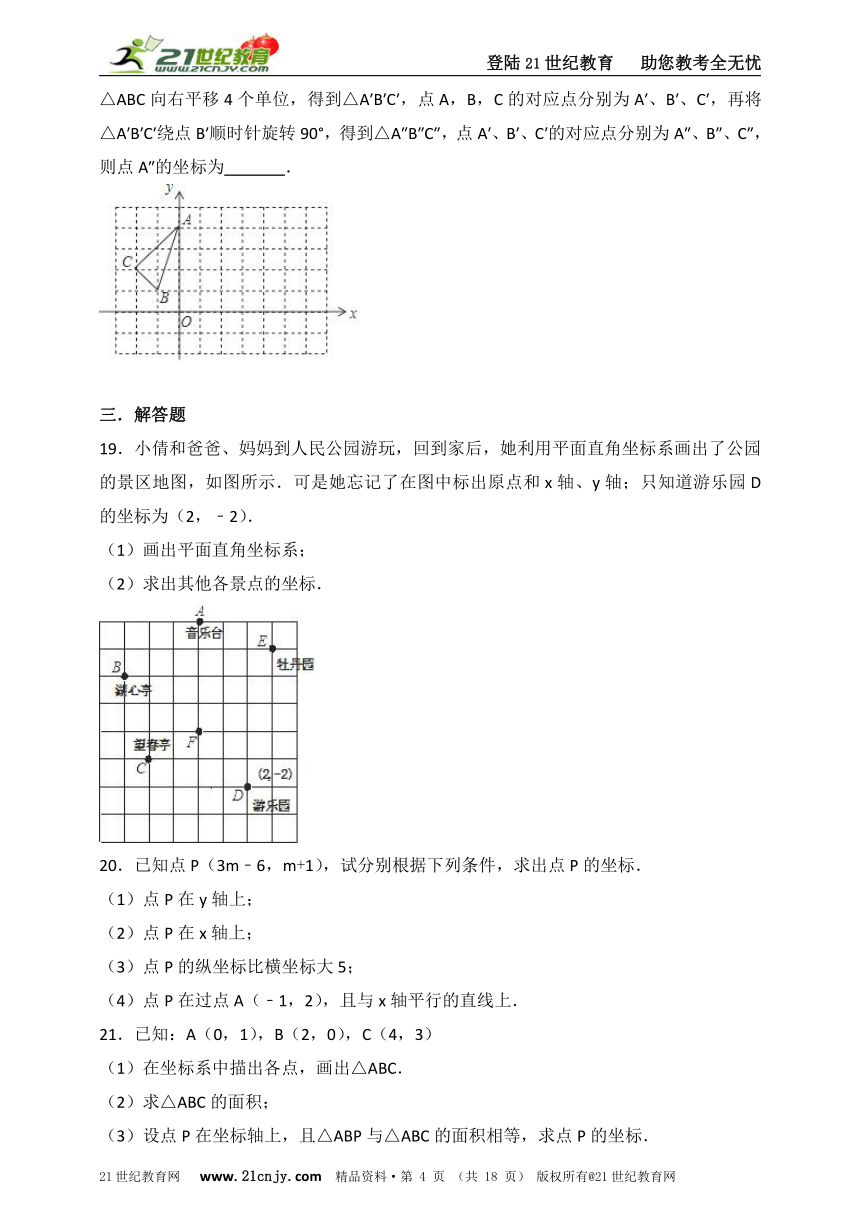
19．小倩和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示．可是她忘记了在图中标出原点和x轴、y轴；只知道游乐园D的坐标为（2，﹣2）．
（1）画出平面直角坐标系；
（2）求出其他各景点的坐标．
20．已知点P（3m﹣6，m+1），试分别根据下列条件，求出点P的坐标．
（1）点P在y轴上；
（2）点P在x轴上；
（3）点P的纵坐标比横坐标大5；
（4）点P在过点A（﹣1，2），且与x轴平行的直线上．
21．已知：A（0，1），B（2，0），C（4，3）
（1）在坐标系中描出各点，画出△ABC．
（2）求△ABC的面积；
（3）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．
22．已知点A（2a﹣b，5+a），B（2b﹣1，﹣a+b）．
（1）若点A、B关于x轴对称，求a、b的值；
（2）若A、B关于y轴对称，求（4a+b）2016的值．
23．如图在平面直角坐标系中，△ABC各顶点的坐标分别为：A（4，0），B（﹣1，4），C（﹣3，1）2·1·c·n·j·y
（1）在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称；
（2）写出点A′B′C′的坐标．
24．阅读理解：我们知道，任意两点关于它们所连线段的中点成中心对称，在平面直角坐标系中，任意两点P（x1，y1）、Q（x2，y2）的对称中心的坐标为（，）．
观察应用：
（1）如图，在平面直角坐标系中，若点P1（0，﹣1）、P2（2，3）的对称中心是点A，则点A的坐标为　 　；21*cnjy*com
（2）另取两点B（﹣1.6，2.1）、C（﹣1，0）．有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动，即第一次跳到点P1关于点A的对称点P2处，接着跳到点P2关于点B的对称点P3处，第三次再跳到点P3关于点C的对称点P4处，第四次再跳到点P4关于点A的对称点P5处，…则点P3、P8的坐标分别为　 　、　 　．
拓展延伸：
（3）求出点P2017的坐标，并直接写出在x轴上与点P2017，点C构成等腰三角形的点的坐标．
25．在平面直角坐标系中，已知点O为坐标原点，点A（0，4）．△AOB是等边三角形，点B在第一象限．
（1）如图①，求点B的坐标；
（2）如图②，点P是x轴上的一点P （，0），连接AP，以点A为旋转中心，把△AOP逆时针旋转，使边AO与AB重合，得△ABD，求此时点D的坐标．
26．在如图所示的直角坐标系中，△ABC的顶点坐标分别是A（﹣4，﹣1），B（1，1），C（﹣1，4）；点P（x1，y1）是△ABC内一点，当点P（x1，y1）平移到点P′（x1+4，y1+1）时．
①请写出平移后新△A1B1C1三个顶点的坐标；
②求△A1B1C1的面积．
　
答案与解析
一．选择题
1．【分析】找到纵坐标为0，且横坐标为2的绝对值的坐标即可．
【解答】解：∵点在x轴上，
∴点的纵坐标为0，
∵点到原点的距离为2，
∴点的横坐标为±2，
∴所求的坐标是（2，0）或（﹣2，0），故选C．
　
2．【分析】直接利用x轴上点的纵坐标为0，进而得出答案．
【解答】解：∵点P（x+3，x﹣4）在x轴上，
∴x﹣4=0，
解得：x=4，
故选：D．
　
3．【分析】根据关于y轴对称的点的横坐标互为相反数，纵坐标相等，可得答案．
【解答】解：点A（a﹣2，3）和点B（﹣1，b+5）关于y轴对称，得
a﹣2=1，b+5=3．
解得a=3，b=﹣2．
则点C（a，b）在第四象限，
故选：D．
　
4．【分析】直接利用已知点坐标进而得出原点位置，进而得出答案．
【解答】解：如图所示：所在位置的坐标为：（0，﹣1）．
故选：D．
　
5．【分析】根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．
【解答】解：点P（m，2）与点Q（3，n）关于原点对称，得
m=﹣3，n=﹣2，
故选：C．
　
6．【分析】根据第二象限内点的横坐标是负数，纵坐标是正数，点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度求出点P的横坐标与纵坐标，然后写出即可．
【解答】解：∵点P在第二象限内，到x轴的距离是4，到y轴的距离是5，
∴点P的横坐标为﹣5，纵坐标为4，
∴点P的坐标为（﹣5，4）．
故选A．
　
7．【分析】分别写出点（a，a）a≠0关于x轴轴对称、关于直线y=﹣x轴对称和关于原点中心对称的对应点的坐标即可．www.21-cn-jy.com
【解答】解：点（a，a）关于x轴轴对称的对应点的坐标为（a，﹣a）；
点（a，a）关于直线y=﹣x对称的对应点的坐标为（﹣a，﹣a）；
点（a，a）a≠0关于原点对称的对应点的坐标为（﹣a，﹣a）．
故选B．
　
8．【分析】根据网格结构，可以利用一对对应点的平移关系解答．
【解答】解：根据网格结构，观察对应点A、D，点A向左平移5个单位，再向下平移2个单位即可到达点D的位置，
所以平移步骤是：先把△ABC向左平移5个单位，再向下平移2个单位．
故选：A．
　
9．【分析】根据横坐标，右移加，左移减；纵坐标，上移加，下移减可得线段AB向右平移1个单位，向上平移1个单位，进而可得a、b的值．【来源：21·世纪·教育·网】
【解答】解：∵A、B两点的坐标分别为（2，0）、（0，1），平移后A1（3，b），B1（a，2），
∴线段AB向右平移1个单位，向上平移1个单位，
∴a=0+1=1，b=0+1=1，
故选：D．
　
10．【分析】先根据点A的坐标求出正方形的边长，再根据旋转可得点C′在第一象限的平分线上，然后求解即可．
【解答】解：∵点A的坐标为（2，0），
∴正方形OABC的边长为2，
∵正方形OABC绕点O顺时针旋转45°，得到正方形OA′B′C′，
∴点C′在第一象限的平分线上，
∴点C′的横坐标为2×=，
纵坐标为为2×=，
∴点C′的坐标为（，）．
故选A．
　
11．【分析】由图象可知点B2016在第一象限，求出B2，B4，B6的坐标，探究规律后即可解决问题．2-1-c-n-j-y
【解答】解：由图象可知点B2016在第一象限，
∵OA=，OB=4，∠AOB=90°，
∴AB===，
∴B2（10，4），B4（20，4），B6（30，4），…
∴B2016（10080，4）．
∴点B2016纵坐标为10080．
故选D．
　
12．【分析】连接AA′，CC′，线段AA′、CC′的垂直平分线的交点就是点P．
【解答】解：由图形可知，对应点的连线CC′、AA′的垂直平分线的交点是点（1，﹣1），
根据旋转变换的性质，点（1，﹣1）即为旋转中心．
故旋转中心坐标是P（1，﹣1）．
故选C．
　
二．填空题
13．【分析】根据在x轴上方的点的纵坐标为正，点到y轴的距离为点的横坐标的绝对值即可得解．
【解答】解：∵点A在x轴上方，到x轴的距离是3，
∴点A的纵坐标是3，
∵点A到y轴的距离是4，
∴点A的横坐标是4或﹣4．
∴点A的坐标是（4，3）或（﹣4，3）．
故答案为：（4，3）或（﹣4，3）．
　
14．【分析】直接利用关于x轴对称点的性质得出a，b的值，进而得出答案．
【解答】解：∵P1（a﹣1，5）和P2（2，b﹣1）关于x轴对称，
∴a﹣1=2，b﹣1=﹣5，
解得：a=3，b=﹣4，
∴（a+b）2017=（3﹣4）2017=﹣1．
故答案为：﹣1．
　
15．【分析】先根据两三角形的对应点确定出对称中心，然后求解即可．
【解答】解：由图可知，△ABC关于点（﹣1，0）对称变换得到△A′B′C′，
∵△ABC上的点P的坐标为（a，b），
∴它的对应点P′的坐标为（﹣a﹣2，﹣b）．
故答案为：（﹣a﹣2，﹣b）．
　
16．【分析】由△ABC中任意一点P（x0，y0），经平移后对应点为P1（x0+7，y0+2）可得△ABC的平移规律为：向右平移7个单位，向上平移2个单位，由此得到点A′的对应点A的坐标．21教育网
【解答】解：根据题意，可得△ABC的平移规律为：向右平移7个单位，向上平移2个单位，
∵A′的坐标为（5，3），
∴它对应的点A的坐标为（﹣2，1）．
故答案为：（﹣2，1）．
　
17．【分析】首先求出P1～P5的坐标，探究规律后，利用规律解决问题．
【解答】解：第一次P1（5，2），
第二次P2（8，1），
第三次P3（10，1），
第四次P4（13，2），
第五次P5（17，2），
…
发现点P的位置4次一个循环，
∵2017÷4=504余1，
P2017的纵坐标与P1相同为2，横坐标为1+12×504+4=6053，
∴P2017（6053，2），
故答案为（6053，2）．
　
18．【分析】由平移的性质和旋转的性质作出图形，即可得出答案．
【解答】解：如图所示：
∵A（0，4），B（﹣1，1），C（﹣2，2），将△ABC向右平移4个单位，得到△A′B′C′，
∴A′、B′、C′的坐标分别为（4，4），B（3，1），C（2，2），
再将△A′B′C′绕点B′顺时针旋转90°，得到△A″B″C″，
则点A″的坐标为 （6，0）；
故答案为：（6，0）．
　
三．解答题
19．【分析】（1）根据游乐园D的坐标为（2，﹣2）即可确定平面直角坐标系；
（2）根据（1）建立的平面直角坐标系进而写出各个点的坐标．
【解答】解：（1）如图所示：
（2）A（0，4），B（﹣3，2），C（﹣2，﹣1），E（3，3），F（0，0）．
　
20．【分析】（1）根据y轴上点的横坐标为0列方程求出m的值，再求解即可；
（2）根据x轴上点的纵坐标为0列方程求出m的值，再求解即可；
（3）根据纵坐标与横坐标的关系列方程求出m的值，再求解即可；
（4）根据平行于x轴的直线上的点的纵坐标相同列方程求出m的值，再求解即可．
【解答】解：（1）∵点P（3m﹣6，m+1）在y轴上，
∴3m﹣6=0，
解得m=2，
∴m+1=2+1=3，
∴点P的坐标为（0，3）；
（2）点P（3m﹣6，m+1）在x轴上，
∴m+1=0，
解得m=﹣1，
∴3m﹣6=3×（﹣1）﹣6=﹣9，
∴点P的坐标为（﹣9，0）；
（3）∵点P（3m﹣6，m+1）的纵坐标比横坐标大5，
∴m+1﹣（3m﹣6）=5，
解得m=1，
∴3m﹣6=3×1﹣6=﹣3，
m+1=1+1=2，
∴点P的坐标为（﹣3，2）；
（4）∵点P（3m﹣6，m+1）在过点A（﹣1，2）且与x轴平行的直线上，
∴m+1=2，
解得m=1，
∴3m﹣6=3×1﹣6=﹣3，
m+1=1+1=2，
∴点P的坐标为（﹣3，2）．
　
21．【分析】（1）确定出点A、B、C的位置，连接AC、CB、AB即可；
（2）过点C向x、y轴作垂线，垂足为D、E，△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积；21世纪教育网版权所有
（3）当点p在x轴上时，由△ABP的面积=4，求得：BP=8，故此点P的坐标为（10，0）或（﹣6，0）；当点P在y轴上时，△ABP的面积=4，解得：AP=4．所以点P的坐标为（0，5）或（0，﹣3）．21·cn·jy·com
【解答】解：（1）如图所示：
（2）过点C向x、y轴作垂线，垂足为D、E．
∴四边形DOEC的面积=3×4=12，△BCD的面积==3，△ACE的面积==4，△AOB的面积==1．21·世纪*教育网
∴△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积
=12﹣3﹣4﹣1=4．
当点p在x轴上时，△ABP的面积==4，即：，解得：BP=8，
所点P的坐标为（10，0）或（﹣6，0）；
当点P在y轴上时，△ABP的面积==4，即，解得：AP=4．
所以点P的坐标为（0，5）或（0，﹣3）．
所以点P的坐标为（0，5）或（0，﹣3）或（10，0）或（﹣6，0）．
　
22．【分析】（1）根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”列方程组求解即可得到a、b的值；www-2-1-cnjy-com
（2）根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”列方程组求出a、b的值，然后代入代数式进行计算即可得解．【版权所有：21教育】
【解答】解：（1）∵点A、B关于x轴对称，
∴，
解得，；
（2）∵A、B关于y轴对称，
∴，
解得，
所以，（4a+b）2016=（﹣4+3）2016=1．
　
23．【分析】（1）根据关于x轴对称的点的坐标特征得到点A′的坐标为（4，0），点B′的坐标为（﹣1，﹣4），点C′的坐标为（﹣3，﹣1），然后描点；21教育名师原创作品
（2）由（1）可得到三个对应点的坐标．
【解答】解：（1）如图，
（2）点A′的坐标为（4，0），点B′的坐标为（﹣1，﹣4），点C′的坐标为（﹣3，﹣1）．
　
24．【分析】（1）直接利用题目所给公式即可求出点A的坐标；
（2）首先利用题目所给公式求出P2的坐标，然后利用公式求出对称点P3的坐标，依此类推即可求出P8的坐标；【来源：21cnj*y.co*m】
（3）由于P1（0，﹣1）→P2（2，3）→P3（﹣5.2，1.2）→P4（3.2，﹣1.2）→P5（﹣1.2，3.2）→P6（﹣2，1）→P7（0，﹣1）→P8（2，3），由此得到P7的坐标和P1的坐标相同，P8的坐标和P2的坐标相同，即坐标以6为周期循环，利用这个规律即可求出点P2017的坐标，也可以根据图形求出在x轴上与点P2017、点C构成等腰三角形的点的坐标．
【解答】解：（1）点A的坐标为（1，1）；
（2）P3、P8的坐标分别为（﹣5.2，1.2），（2，3）；
（3）∵P1（0，﹣1）→P2（2，3）→P3（﹣5.2，1.2）→P4（3.2，﹣1.2）→P5（﹣1.2，3.2）→P6（﹣2，1）→P7（0，﹣1）→P8（2，3）；21*cnjy*com
∴P7的坐标和P1的坐标相同，P8的坐标和P2的坐标相同，即坐标以6为周期循环．
∵2017÷6=336…1．
∴P2017的坐标与P1的坐标相同，为P2017（0，﹣1）；
在x轴上与点P2017、点C构成等腰三角形的点的坐标为（﹣1﹣，0），（0，0），（﹣1，0），（1，0）．【出处：21教育名师】
故答案为：（1，1）；（﹣5.2，1.2），（2，3）．
　
25．【分析】（1）过B作BC⊥y轴于C，根据等边三角形的性质得到AC=OC=AO=2，∠AOB=60°，解直角三角形即可得到结论；
（2）由△ABD由△AOP旋转得到，利用旋转的性质得到两三角形全等，利用全等三角形对应边相等，对应角相等得到AP=AD，∠DAB=∠PAO，进而得到三角形ADP为等腰直角三角形，求出AP的长，即为等边三角形的边长，如图1，过点D作DH⊥x轴于点H，延长EB交DH于点G，可得BG⊥DH，在直角三角形BDG中，求出BG与DG的长，进而确定出OH与DH的长，确定出D坐标即可．
【解答】解：（1）过B作BC⊥y轴于C，
∵点A（0，4），
∴OA=4，
∵△AOB是等边三角形，
∴AC=OC=AO=2，∠AOB=60°，
∴BC=OC=2，
∴B（2，2）；
（2）∵△ABD由△AOP旋转得到，
∴△ABD≌△AOP，
∴AP=AD，∠DAB=∠PAO，
∴∠DAP=∠BAO=60°，
∴△ADP是等边三角形，
∴DP=AP==，
如图1，过点D作DH⊥x轴于点H，延长EB交DH于点G，可得BG⊥DH，
在Rt△BDG中，∠BGD=90°，∠DBG=60°，BD=OP==，
∴BG=BD?cos60°=×=，DG=BD?sin60°=×=，
∴OH=EG=，DH=，
∴点D的坐标为（，）．
　
26．【分析】（1）根据点P平移前后的坐标，可得出平移的规律，继而可得出△A1B1C1三个顶点的坐标；21cnjy.com
（2）利用构图法，求解△A1B1C1的面积．
【解答】解：①∵P（x1，y1）平移后点P′（x1+4，y1+1），
∴平移的规律为：向右平移4个单位，向上平移1个单位，
∴A1（0，0），B1（5，2），C1（3，5）；
②S△A1B1C1=S△ABC=5×5﹣×3×5﹣×2×3﹣×2×5=．