第三章 位置与坐标单元检测题C

北师版数学八年级上册第三章《位置与坐标》单元检测题C
　
一．选择题（共12小题）
1．课间操时，小华、小军、小刚的位置如图1，小华对小刚说，如果我的位置用（0，0）表示，小军的位置用（2，1）表示，那么你的位置可以表示成（　　）
A．（5，4） B．（4，5） C．（3，4） D．（4，3）
2．如图，一个点在第一象限及x轴、y轴上运动，且每秒移动一个单位，在第1秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，那么第35秒时质点所在位置的坐标是（　　）
A．（4，0） B．（0，5） C．（5，0） D．（5，5）
3．点P的横坐标是﹣3，且到x轴的距离为5，则P点的坐标是（　　）
A．（5，﹣3）或（﹣5，﹣3） B．（﹣3，5）或（﹣3，﹣5）
C．（﹣3，5） D．（﹣3，﹣5）
4．已知点M（3，﹣2）与点M′（x，y）在同一条平行于x轴的直线上，且M′到y轴的距离等于4，那么点M′的坐标是（　　）
A．（4，2）或（﹣4，2） B．（4，﹣2）或（﹣4，﹣2）
C．（4，﹣2）或（﹣5，﹣2） D．（4，﹣2）或（﹣1，﹣2）
5．已知点A（﹣1，0），B（2，0），在y轴上存在一点C，使三角形ABC的面积为6，则点C的坐标为（　　）
A．（0，4） B．（0，2） C．（0，2）或（0，﹣2） D．（0，4）或（0，﹣4）
6．点P（x，y）在第二象限内，且|x|=2，|y|=3，则点P关于y轴的对称点的坐标为（　　）
A．（2，3） B．（﹣2，﹣3） C．（3，﹣2） D．（﹣3，2）
7．如果A（1﹣a，b+1）关于y轴的对称点在第三象限，那么点B（1﹣a，b）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
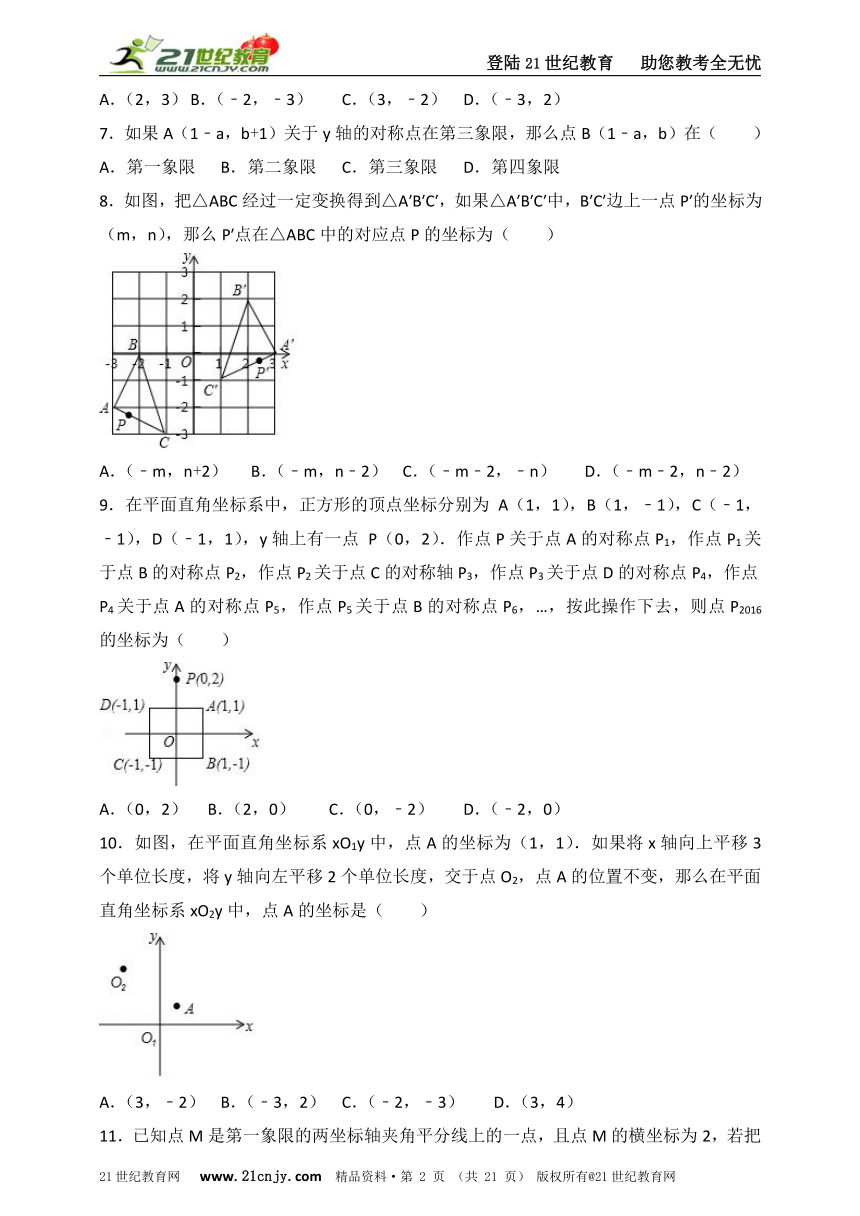
8．如图，把△ABC经过一定变换得到△A′B′C′，如果△A′B′C′中，B′C′边上一点P′的坐标为（m，n），那么P′点在△ABC中的对应点P的坐标为（　　）
A．（﹣m，n+2） B．（﹣m，n﹣2） C．（﹣m﹣2，﹣n） D．（﹣m﹣2，n﹣2）
9．在平面直角坐标系中，正方形的顶点坐标分别为 A（1，1），B（1，﹣1），C（﹣1，﹣1），D（﹣1，1），y轴上有一点 P（0，2）．作点P关于点A的对称点P1，作点P1关于点B的对称点P2，作点P2关于点C的对称轴P3，作点P3关于点D的对称点P4，作点P4关于点A的对称点P5，作点P5关于点B的对称点P6，…，按此操作下去，则点P2016的坐标为（　　）
A．（0，2） B．（2，0） C．（0，﹣2） D．（﹣2，0）
10．如图，在平面直角坐标系xO1y中，点A的坐标为（1，1）．如果将x轴向上平移3个单位长度，将y轴向左平移2个单位长度，交于点O2，点A的位置不变，那么在平面直角坐标系xO2y中，点A的坐标是（　　）
A．（3，﹣2） B．（﹣3，2） C．（﹣2，﹣3） D．（3，4）
11．已知点M是第一象限的两坐标轴夹角平分线上的一点，且点M的横坐标为2，若把点M向左平移个单位，得到点M1，则点M1的坐标是（　　）
A．（﹣2，2） B．（2﹣，2） C．（﹣2，﹣2） D．（2﹣，﹣2）
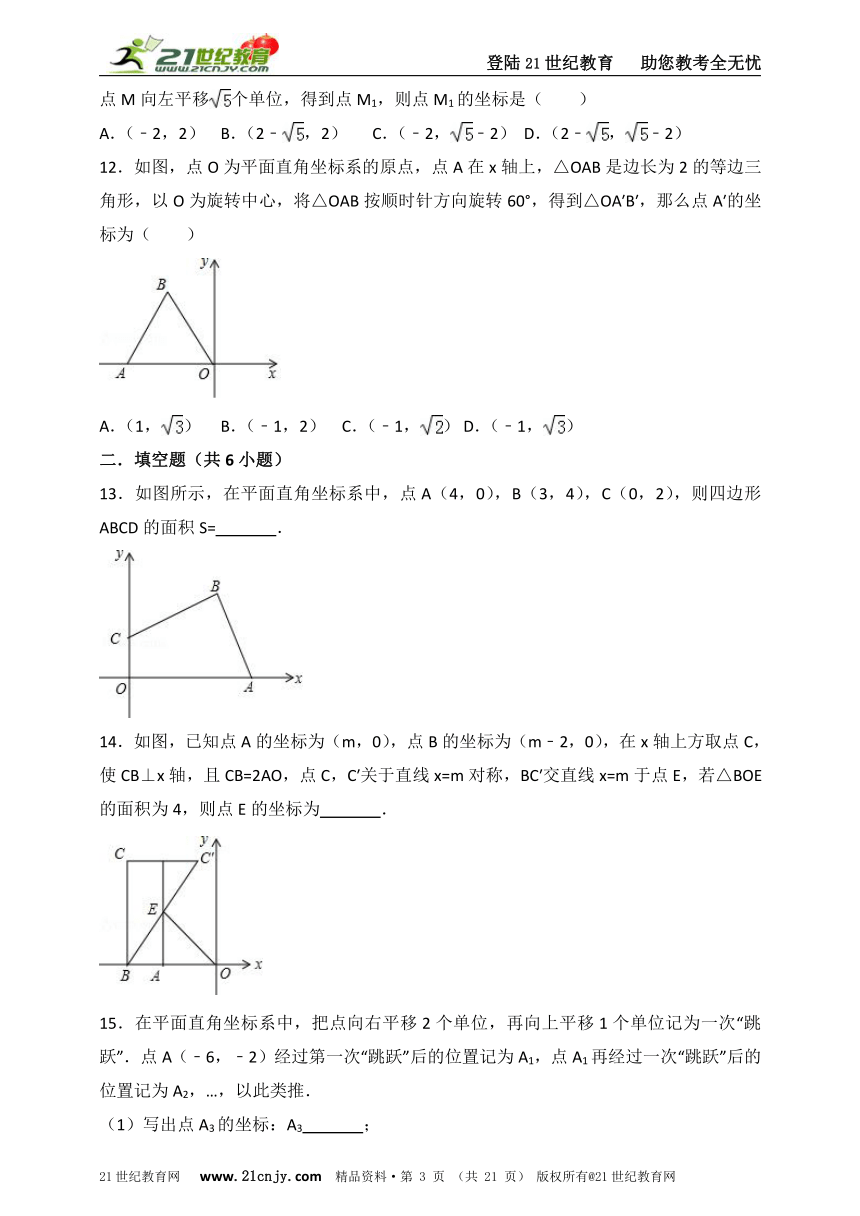
12．如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为2的等边三角形，以O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，那么点A′的坐标为（　　）
A．（1，） B．（﹣1，2） C．（﹣1，） D．（﹣1，）
二．填空题（共6小题）
13．如图所示，在平面直角坐标系中，点A（4，0），B（3，4），C（0，2），则四边形ABCD的面积S=　 　．
14．如图，已知点A的坐标为（m，0），点B的坐标为（m﹣2，0），在x轴上方取点C，使CB⊥x轴，且CB=2AO，点C，C′关于直线x=m对称，BC′交直线x=m于点E，若△BOE的面积为4，则点E的坐标为　 　．
15．在平面直角坐标系中，把点向右平移2个单位，再向上平移1个单位记为一次“跳跃”．点A（﹣6，﹣2）经过第一次“跳跃”后的位置记为A1，点A1再经过一次“跳跃”后的位置记为A2，…，以此类推．
（1）写出点A3的坐标：A3　 　；
（2）写出点An的坐标：An　 　（用含n的代数式表示）．
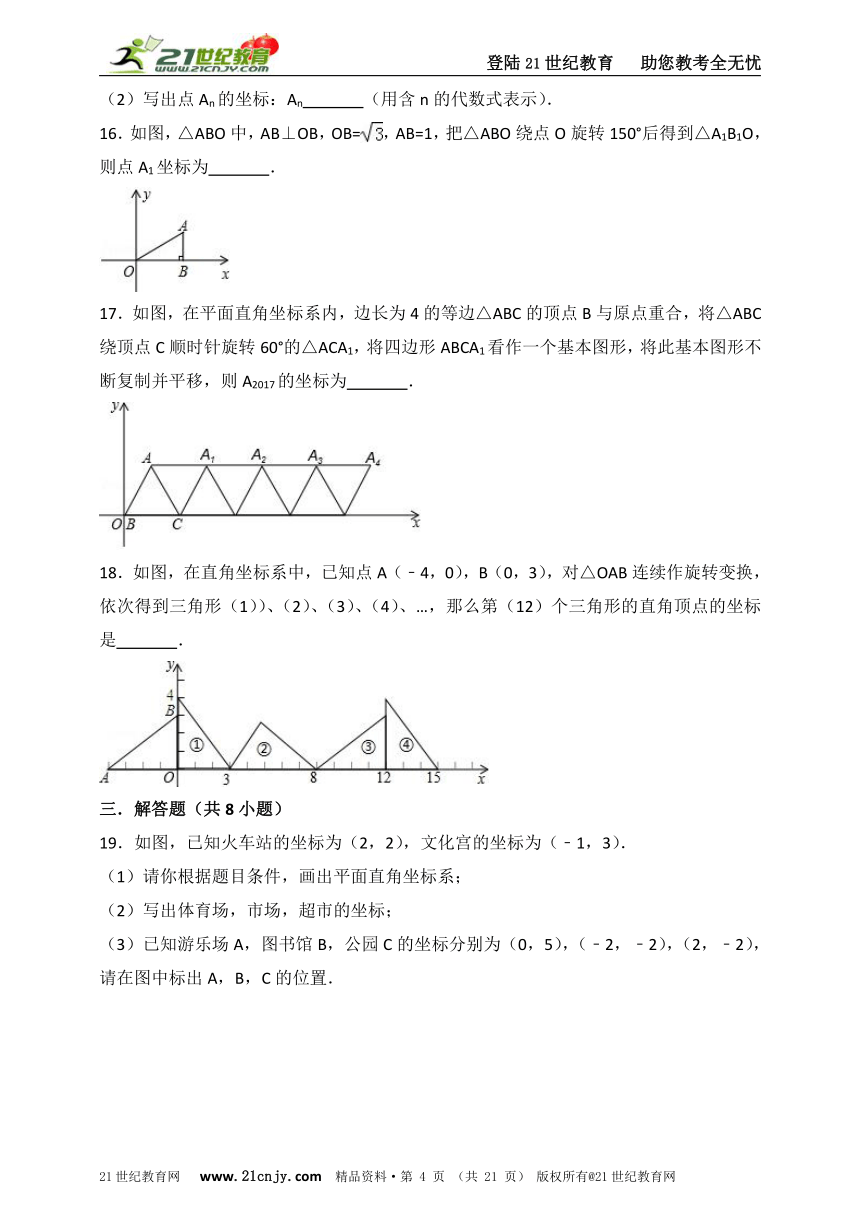
16．如图，△ABO中，AB⊥OB，OB=，AB=1，把△ABO绕点O旋转150°后得到△A1B1O，则点A1坐标为　 　．
17．如图，在平面直角坐标系内，边长为4的等边△ABC的顶点B与原点重合，将△ABC绕顶点C顺时针旋转60°的△ACA1，将四边形ABCA1看作一个基本图形，将此基本图形不断复制并平移，则A2017的坐标为　 　．
18．如图，在直角坐标系中，已知点A（﹣4，0），B（0，3），对△OAB连续作旋转变换，依次得到三角形（1））、（2）、（3）、（4）、…，那么第（12）个三角形的直角顶点的坐标是　 　．
三．解答题（共8小题）
19．如图，已知火车站的坐标为（2，2），文化宫的坐标为（﹣1，3）．
（1）请你根据题目条件，画出平面直角坐标系；
（2）写出体育场，市场，超市的坐标；
（3）已知游乐场A，图书馆B，公园C的坐标分别为（0，5），（﹣2，﹣2），（2，﹣2），请在图中标出A，B，C的位置．
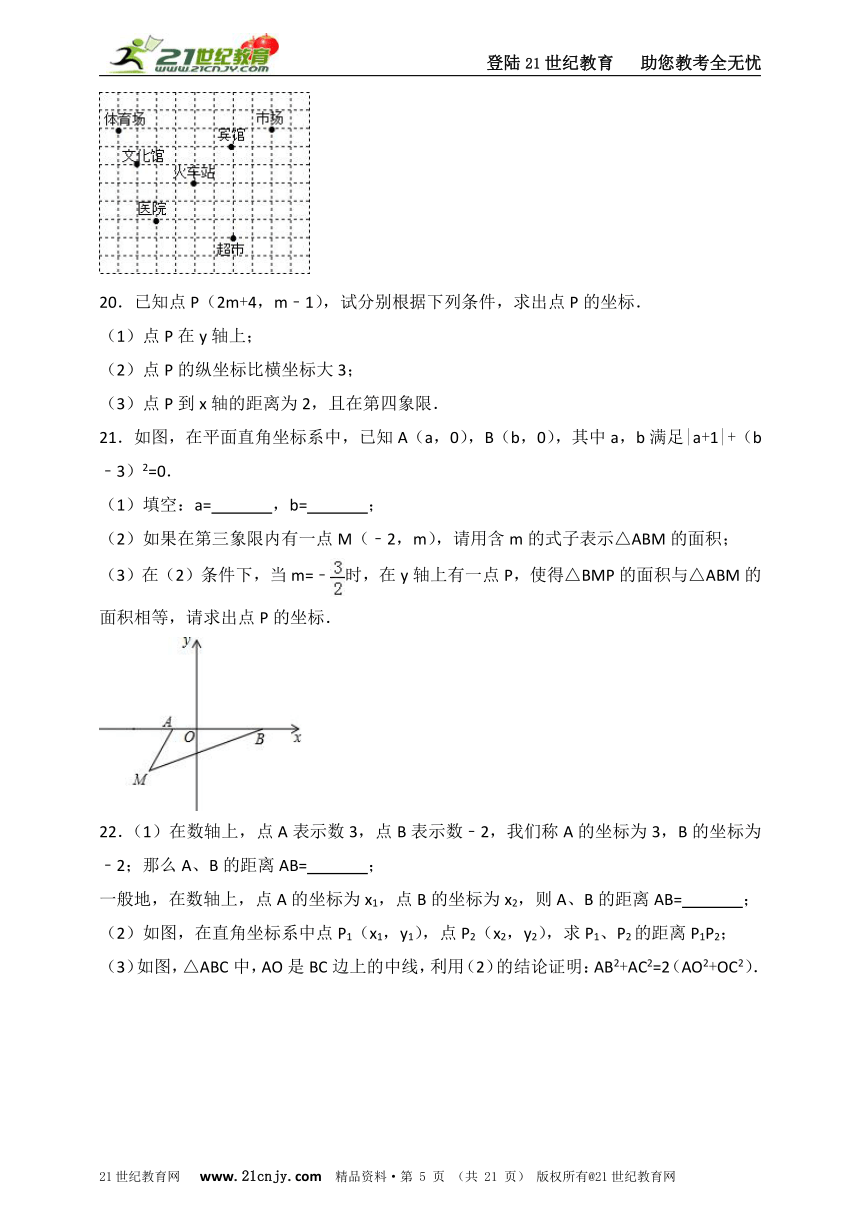
20．已知点P（2m+4，m﹣1），试分别根据下列条件，求出点P的坐标．
（1）点P在y轴上；
（2）点P的纵坐标比横坐标大3；　
（3）点P到x轴的距离为2，且在第四象限．
21．如图，在平面直角坐标系中，已知A（a，0），B（b，0），其中a，b满足|a+1|+（b﹣3）2=0．
（1）填空：a=　 　，b=　 　；
（2）如果在第三象限内有一点M（﹣2，m），请用含m的式子表示△ABM的面积；
（3）在（2）条件下，当m=﹣时，在y轴上有一点P，使得△BMP的面积与△ABM的面积相等，请求出点P的坐标．
22．（1）在数轴上，点A表示数3，点B表示数﹣2，我们称A的坐标为3，B的坐标为﹣2；那么A、B的距离AB=　 　；
一般地，在数轴上，点A的坐标为x1，点B的坐标为x2，则A、B的距离AB=　 　；
（2）如图，在直角坐标系中点P1（x1，y1），点P2（x2，y2），求P1、P2的距离P1P2；
（3）如图，△ABC中，AO是BC边上的中线，利用（2）的结论证明：AB2+AC2=2（AO2+OC2）．
23．如图，在直角坐标系中，A（﹣1，5），B（﹣3，0），C（﹣4，3）．
（1）在图中作出△ABC关于y轴对称的图形△A1B1C1．
（2）写出点C1的坐标．
24．已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．
（1）写出A′、B′、C′的坐标；
（2）求出△ABC的面积；
（3）点P在y轴上，且△BCP与△ABC的面积相等，求点P的坐标．
25．如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
（1）若△ABC经过平移后得到△A1B1C1，已知点C1的坐标为（4，0），写出顶点A1，B1的坐标；
（2）若△ABC和△A2B2C2关于原点O成中心对称图形，写出△A2B2C2的各顶点的坐标；
（3）将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3，写出△A3B3C3的各顶点的坐标．
26．如图，在平面直角坐标系中，一个方格的边长为1个单位长度，三角形MNQ是三角形ABC经过某种变换后得到的图形．
（1）请分别写出点A与点M，点B与点N，点C与点Q的坐标，并观察它们之间的关系；
（2）已知点P是三角形ABC内一点，其坐标为（﹣3，2），探究其在三角形MNQ中的对应点R的坐标，并猜想线段AC和线段MQ的关系．
　
答案与解析
　
一．选择题
1．【分析】根据已知两点的坐标确定平面直角坐标系，然后确定其它各点的坐标．
【解答】解：如果小华的位置用（0，0）表示，小军的位置用（2，1）表示，如图所示就是以小华为原点的平面直角坐标系的第一象限，所以小刚的位置为（4，3）．
故选D．
　
2．【分析】根据质点移动的各点的坐标与时间的关系，找出规律即可解答．
【解答】解：由题意可知质点移动的速度是1个单位长度/每秒，
到达（1，0）时用了3秒，到达（2，0）时用了4秒，
从（2，0）到（0，2）有四个单位长度，则到达（0，2）时用了4+4=8秒，到（0，3）时用了9秒；
从（0，3）到（3，0）有六个单位长度，则到（3，0）时用9+6=15秒；
依此类推到（4，0）用16秒，到（0，4）用16+8=24秒，到（0，5）用25秒，到（5，0）用25+10=35秒．
故第35秒时质点到达的位置为（5，0），
故选：C．
　
3．【分析】点P到x轴的距离为5即P点的纵坐标是5或﹣5，又因为点P的横坐标是﹣3，即可得P点坐标．
【解答】解：∵点P到x轴的距离为5，
∴P点的纵坐标是5或﹣5，
∵点P的横坐标是﹣3，
∴P点的坐标是（﹣3，5）或（﹣3，﹣5）．
故选B．
　
4．【分析】由点M和M′在同一条平行于x轴的直线上，可得点M′的纵坐标；由“M′到y轴的距离等于4”可得，M′的横坐标为4或﹣4，即可确定M′的坐标．
【解答】解：∵M（3，﹣2）与点M′（x，y）在同一条平行于x轴的直线上，
∴M′的纵坐标y=﹣2，
∵“M′到y轴的距离等于4”，
∴M′的横坐标为4或﹣4．
所以点M′的坐标为（4，﹣2）或（﹣4，﹣2），故选B．
　
5．【分析】直接利用三角形面积公式结合坐标系得出符合题意的答案．
【解答】解：如图所示：点A（﹣1，0），B（2，0），三角形ABC的面积为6，
则点C的坐标为：（0，4）或（0，﹣4）．
故选：D．
　
6．【分析】根据第二象限内点的横坐标小于零，纵坐标小于零，可得P点坐标，根据关于y轴对称的点的横坐标互为相反数，纵坐标相等，可得答案．
【解答】解：P（x，y）在第二象限内，且|x|=2，|y|=3，则点P（﹣2，3），
点P关于y轴的对称点的坐标为（2，3），
故选：A．
　
7．【分析】根据关于y轴对称的点，纵坐标相同，横坐标互为相反数，可得答案．
【解答】解：A（1﹣a，b+1）关于y轴的对称点在第三象限，得
（1﹣a，b+1）在第四象限，
1﹣a＞0，b+1＜0，
1﹣a＞0，b＜﹣1，
（1﹣a，b）在第四象限，
故选：D．
　
8．【分析】根据已知三对对应点的坐标，得出变换规律，再让点P的坐标也做相应变化即可．
【解答】解：∵A（﹣3，﹣2），B（﹣2，0），C（﹣1，﹣3），
A′（3，0），B′（2，2），C′（1，﹣1），
∴横坐标互为相反数；纵坐标增加了0﹣（﹣2）=2﹣0=﹣1﹣（﹣3）=2；
∵B′C′边上一点P′的坐标为（m，n），
∴点P′变换前的对应点P的坐标为（﹣m，n﹣2）．
故选B．
　
9．【分析】从特殊到一般寻找规律，发现从P5开始出现循环，由此即可解决问题．
【解答】解：由题意P1（2，0），P2（0，﹣2），P3（﹣2，0），P4（0，2），P5（2，0），…P5与P1重合，从P5开始出现循环，
2016÷4=504，
∴P2016与P4重合，
∴P2016（0，2）．
故选A．
　
10．【分析】把x轴向上平移3个单位长度，将y轴向左平移2个单位长度理解为把点A向下平移3个单位长度，再向右平移2个单位，然后根据点平移的坐标规律求解．
【解答】解：x轴向上平移3个单位长度，将y轴向左平移2个单位长度相当于把点A向下平移3个单位长度，再向右平移2个单位，
所以在平面直角坐标系xO2y中，点A的坐标是（3，﹣2）．
故选A．
　
11．【分析】先根据点M是第一象限的两坐标轴夹角平分线上的一点，且点M的横坐标为2，得到点M的坐标，再根据平移的方向与距离，即可得出点M1的坐标．
【解答】解：∵点M是第一象限的两坐标轴夹角平分线上的一点，且点M的横坐标为2，
∴M（2，2），
∵把点M向左平移个单位，横坐标减小，纵坐标不变，
∴得到M1（2﹣，2），
故选：B．
　
12．【分析】作BC⊥x轴于C，如图，根据等边三角形的性质得OA=OB=2，AC=OC=1，∠BOA=60°，则易得A点坐标和O点坐标，再利用勾股定理计算出BC=，然后根据第二象限点的坐标特征可写出B点坐标；由旋转的性质得∠AOA′=∠BOB′=60°，OA=OB=OA′=OB′，则点A′与点B重合，于是可得点A′的坐标．
【解答】解：作BC⊥x轴于C，如图，
∵△OAB是边长为2的等边三角形
∴OA=OB=2，AC=OC=1，∠BOA=60°，
∴A点坐标为（﹣2，0），O点坐标为（0，0），
在Rt△BOC中，BC==，
∴B点坐标为（﹣1，）；
∵△OAB按顺时针方向旋转60°，得到△OA′B′，
∴∠AOA′=∠BOB′=60°，OA=OB=OA′=OB′，
∴点A′与点B重合，即点A′的坐标为（﹣1，），
故选D．
　
二．填空题
13．【分析】连接OB，根据S四边形ABCO=S△ABO+S△BCO即可计算．
【解答】解：如图，连接OB．
∵点A（4，0），B（3，4），C（0，2），
∴S四边形ABCO=S△ABO+S△BCO=?4?4+?2?3=11．
故答案为11．
　
14．【分析】先根据矩形的性质与轴对称的性质得出AB=C′D，再利用AAS证明△ABE≌△DC′E，得出AE=DE=﹣m．根据△BOE的面积为4，列出方程（2﹣m）（﹣m）=4，解方程即可．
【解答】解：如图，设AE与CC′交于点D．
∵点A的坐标为（m，0），在x轴上方取点C，使CB⊥x轴，且CB=2AO，
∴CB=﹣2m．
∵点C，C′关于直线x=m对称，
∴CD=C′D，
∵ABCD是矩形，AB=CD，
∴AB=C′D．
又∵∠BAE=∠C′DE=90°，∠AEB=DEC′，
∴△ABE≌△DC′E，
∴AE=DE，
∴AE=AD=BC=﹣m．
∵△BOE的面积为4，
∴（2﹣m）（﹣m）=4，
整理得，m2﹣2m﹣8=0，
解得m=4或﹣2，
∵在x轴上方取点C，
∴﹣2m＞0，
∴m＜0，
∴m=4不合题意舍去，
∵点E的坐标为（m，﹣m），
∴点E的坐标为（﹣2，2）．
故答案为（﹣2，2）．
　
15．【分析】（1）根据坐标平移特点：右加左减、上加下减，即可得出答案；
（2）根据（1）中规律可得．
【解答】解：（1）根据题意知，A1坐标为（﹣6+2，﹣2+1），即（﹣4，﹣1），
A2坐标为（﹣6+2×2，﹣2+1×2），即（﹣2，0），
A3坐标为（﹣6+2×3，﹣2+1×3），即（0，1），
故答案为：（0，1）；
（2）由（1）知，点An的坐标为（﹣6+2n，﹣2+n），
故答案为：（﹣6+2n，﹣2+n）．
　
16．【分析】需要分类讨论：在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标．
【解答】解：∵△ABO中，AB⊥OB，OB=，AB=1，
∴tan∠AOB=，
∴∠AOB=30°．
如图1，当△ABO绕点O顺时针旋转150°后得到△A1B1O，
则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°，
则易求A1（﹣1，）；
如图2，当△ABO绕点O逆时针旋转150°后得到△A1B1O，
则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°，
则易求A1（﹣2，0）；
综上所述，点A1的坐标为（﹣1，）或（﹣2，0）；
故答案为：（﹣1，）或（﹣2，0）．
　
17．【分析】根据等边三角形的性质易得OA=BC=4，∠AOC=60°．过点A作AD⊥x轴于D，求出BD=DC=BC=2，AD=OA?sin∠AOD=4×=2，那么A（2，2）．再利用旋转与平移的性质分别求出A1（2+4，2），A2（2+4×2，2），A3（2+4×3，2），依此类推即可求出A2017的坐标．
【解答】解：∵边长为4的等边△ABC的顶点B与原点重合，
∴OA=BC=4，∠AOC=60°，
如图，过点A作AD⊥x轴于D，
∴BD=DC=BC=2，AD=OA?sin∠AOD=4×=2，
∴A（2，2）．
∵将△ABC绕顶点C顺时针旋转60°的△ACA1，
∴四边形AOCA1是平行四边形，
∴AA1=OC=4，AA1∥OC，
∴A1（2+4，2），即A1（6，2）；
∵将四边形ABCA1看作一个基本图形，将此基本图形不断复制并平移，
∴A2（2+4×2，2），即A2（10，2）；
A3（2+4×3，2），即A3（14，2）；
…
∴A2017的坐标为（2+4×2017，2），即A2017（8070，2）；
故答案为（8070，2）．
　
18．【分析】观察不难发现，每三次旋转为一个循环组依次循环，第7个直角三角形的直角顶点与第6个直角三角形的直角顶点重合，然后求出一个循环组旋转过的距离，即可得解．
【解答】解：由图可知，第4个三角形与第1个三角形的所处形状相同，即每三次旋转为一个循环组依次循环，
∵一个循环组旋转过的长度为12，
∴12×12÷3=48，
∴第（12）个三角形的直角顶点坐标是（48，0）．
故答案为：（48，0）．
　
三．解答题
19．【分析】（1）火车站向左2个单位，向下2个单位确定出坐标原点，然后建立平面直角坐标系即可；
（2）根据平面直角坐标系写出各位置的坐标即可；
（3）根据三点坐标，标出即可．
【解答】解：（1）如图：
（2）体育场（﹣2，5）、市场（6，5）、超市（4，﹣1）；
（3）如上图所示．
　
20．【分析】（1）根据y轴上点的横坐标为0列方程求出m的值，再求解即可；
（2）根据纵坐标比横坐标大3列方程求解m的值，再求解即可；
（3）根据点P到x轴的距离列出绝对值方程求解m的值，再根据第四象限内点的横坐标是正数，纵坐标是负数求解．
【解答】解：（1）∵点P（2m+4，m﹣1）在y轴上，
∴2m+4=0，
解得m=﹣2，
所以，m﹣1=﹣2﹣1=﹣3，
所以，点P的坐标为（0，﹣3）；
（2）∵点P的纵坐标比横坐标大3，
∴（m﹣1）﹣（2m+4）=3，
解得m=﹣8，
m﹣1=﹣8﹣1=﹣9，
2m+4=2×（﹣8）+4=﹣12，
所以，点P的坐标为（﹣12，﹣9）；
（3）∵点P到x轴的距离为2，
∴|m﹣1|=2，
解得m=﹣1或m=3，
当m=﹣1时，2m+4=2×（﹣1）+4=2，
m﹣1=﹣1﹣1=﹣2，
此时，点P（2，﹣2），
当m=3时，2m+4=2×3+4=10，
m﹣1=3﹣1=2，
此时，点P（10，2），
∵点P在第四象限，
∴点P的坐标为（2，﹣2）．
　
21．【分析】（1）根据非负数性质可得a、b的值；
（2）根据三角形面积公式列式整理即可；
（3）先根据（2）计算S△ABM，再分两种情况：当点P在y轴正半轴上时、当点P在y轴负半轴上时，利用割补法表示出S△BMP，根据S△BMP=S△ABM列方程求解可得．
【解答】解：（1）∵|a+1|+（b﹣3）2=0，
∴a+1=0且b﹣3=0，
解得：a=﹣1，b=3，
故答案为：﹣1，3；
（2）过点M作MN⊥x轴于点N，
∵A（﹣1，0）B（3，0）
∴AB=1+3=4，
又∵点M（﹣2，m）在第三象限
∴MN=|m|=﹣m
∴S△ABM=AB?MN=×4×（﹣m）=﹣2m；
（3）当m=﹣时，M（﹣2，﹣）
∴S△ABM=﹣2×（﹣）=3，
点P有两种情况：①当点P在y轴正半轴上时，设点p（0，k）

S△BMP=5×（+k）﹣×2×（+k）﹣×5×﹣×3×k=k+，
∵S△BMP=S△ABM，
∴k+=3，
解得：k=0.3，
∴点P坐标为（0，0.3）；
②当点P在y轴负半轴上时，设点p（0，n），
S△BMP=﹣5n﹣×2×（﹣n﹣）﹣×5×﹣×3×（﹣n）=﹣n﹣，
∵S△BMP=S△ABM，
∴﹣n﹣=3，
解得：n=﹣2.1
∴点P坐标为（0，﹣2.1），
故点P的坐标为（0，0.3）或（0，﹣2.1）．
　
22．【分析】（1）直接根据数轴上两点间的距离公式进行解答；
（2）根据坐标系内两点间的距离公式进行解答；
（3）分别设出A、B、C三点的坐标，再根据两点间的距离公式得出AB2+AC2及AO2+OC2的值，进而可得出结论．
【解答】解：（1）∵在数轴上，点A表示数3，点B表示数﹣2，
∴A、B的距离AB=|﹣2﹣3|=5，
∴一般地，在数轴上，点A的坐标为x1，点B的坐标为x2，则A、B的距离AB=|x1﹣x2|；
（2）∵在直角坐标系中点P1（x1，y1），点P2（x2，y2），
∴P1P2=；
（3）设A（a，d），C（c，0）
∵O是BC的中点，
∴B（﹣c，0）
∴AB2+AC2=（a+c）2+d2+（a﹣c）2+d2=2（a2+c2+d2），AO2+OC2=a2+d2+c2，
∴AB2+AC2=2（AO2+OC2）．
　
23．【分析】（1）根据轴对称的定义直接画出．
（2）由点位置直接写出坐标．
【解答】解：（1）如图所示：
（2）点C1的坐标为：（4，3）．
　
24．【分析】（1）根据图形平移的性质画出△A′B′C′即可；根据各点在坐标系中的位置写出点A′、B′、C′的坐标；
（2）根据三角形的面积公式即可求出结果；
（3）设P（0，y），再根据三角形的面积公式求出y的值即可．
【解答】解：（1）如图所示：A′（0，4）、B′（﹣1，1）、C′（3，1）；
（2）S△ABC=×（3+1）×3=6；
（3）设点P坐标为（0，y），
∵BC=4，点P到BC的距离为|y+2|，
由题意得×4×|y+2|=6，
解得y=1或y=﹣5，
所以点P的坐标为（0，1）或（0，﹣5）．
　
25如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
（1）若△ABC经过平移后得到△A1B1C1，已知点C1的坐标为（4，0），写出顶点A1，B1的坐标；
（2）若△ABC和△A2B2C2关于原点O成中心对称图形，写出△A2B2C2的各顶点的坐标；
（3）将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3，写出△A3B3C3的各顶点的坐标．
【分析】（1）利用点C和点C1的坐标变化得到平移的方向与距离，然后利用此平移规律写出顶点A1，B1的坐标；
（2）根据关于原点对称的点的坐标特征求解；
（3）利用网格和旋转的性质画出△A2B3C3，然后写出△A2B3C3的各顶点的坐标．
【解答】解：（1）如图，△A1B1C1为所作，
因为点C（﹣1，3）平移后的对应点C1的坐标为（4，0），
所以△ABC先向右平移5个单位，再向下平移3个单位得到△A1B1C1，
所以点A1的坐标为（2，2），B1点的坐标为（3，﹣2）；
（2）因为△ABC和△A1B2C2关于原点O成中心对称图形，
所以A2（3，﹣5），B2（2，﹣1），C2（1，﹣3）；
（3）如图，△A2B3C3为所作，A3（5，3），B3（1，2），C3（3，1）；
　
26．【分析】（1）根据平移直角坐标系写出各点的坐标，然后根据关于原点对称的点的特征解答；
（2）根据（1）的结论写出点R的坐标，根据网格结构判断AC∥MQ．
【解答】解：（1）点A（﹣4，1），点M（4，﹣1），
点B（﹣1，2），点N（1，﹣2），
点C（﹣3，4），点Q（3，﹣4），
它们分别关于坐标原点对称；
（2）点P（﹣3，2）的对应点R的坐标为（3，﹣2），
AC∥MQ且相等．