北师大七年级上《第六章数据的收集与整理》专题训练(含答案)
文档属性
| 名称 | 北师大七年级上《第六章数据的收集与整理》专题训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 504.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-19 18:50:56 | ||
图片预览

文档简介
数据的收集与整理专题训练
1.自1939年创办以来,重庆育才中学一直坚守文化底线,不断挑战自我极限,在沧桑文化中愈加根深叶茂.在今年,即将推出的本部改造计划不仅是文化审美层面的颠覆尝试,也是学校发展的巨大工程,其中三种style的民国大门各具特色,A磅礴大气,B清爽简约,C典雅古朴款,为调查民意学校让教职工进行投票呈现了四种结果,喜欢A款、喜欢B款、喜欢C款、都可以,现调查结果如下:
(1)如图,喜欢C款的占20%,喜欢B款的占15%,则调查总人数为,扇形统计图中认为“都可以”的所占圆心角为度;根据题中信息补全条形统计图.
(2)我们学校共有600名教职工,请根据上图估算喜欢A款的有多少人?
2.A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:
竞选人
A
B
C
笔试
85
95
90
口试
80
85
(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角是
度.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
3.2014年3月28日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列两幅统计图(说明:A级:90~100分;B级:75~89分;C级:60~74分;D级:60分以下).请结合图中提供的信息,解答下列问题:
(1)求扇形统计图2中C级所在的扇形的圆心角度数;
(2)请把条形统计图1补充完整并写出计算过程;
(3)若该校共有2000名学生,请你估计安全知识竞赛中A级和B级的学生一共有多少人?
4.林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了
名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
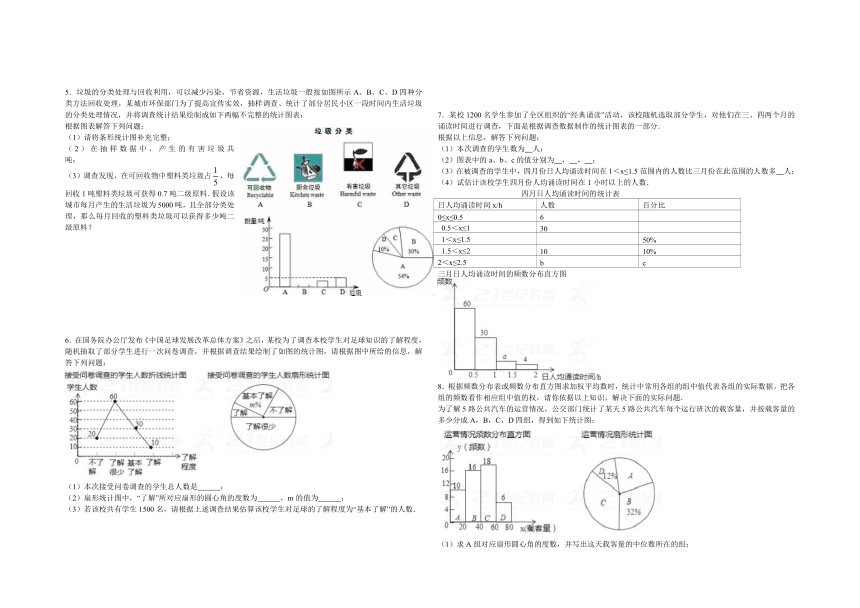
5.垃圾的分类处理与回收利用,可以减少污染,节省资源,生活垃圾一般按如图所示A、B、C、D四种分类方法回收处理,某城市环保部门为了提高宣传实效,抽样调查、统计了部分居民小区一段时间内生活垃圾的分类处理情况,并将调查统计结果绘制成如下两幅不完整的统计图表:
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共
吨;
(3)调查发现,在可回收物中塑料类垃圾占,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
6.在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
(1)本次接受问卷调查的学生总人数是
;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为
,m的值为
;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.
7.某校1200名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
根据以上信息,解答下列问题:
(1)本次调查的学生数为
人;
(2)图表中的a、b、c的值分别为
,
,
;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多
人;
(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.
四月日人均诵读时间的统计表
日人均诵读时间x/h
人数
百分比
0≤x≤0.5
6
0.5<x≤1
30
1<x≤1.5
50%
1.5<x≤2
10
10%
2<x≤2.5
b
c
三月日人均诵读时间的频数分布直方图
8.根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图:
(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
参考答案
1.(1)、60人;66°;图形见解析;(2)、280人.
【解析】
试题分析:(1)、观察统计图,利用喜欢C款的人数除以它所占的百分比即可得到调查的总人数,进一步求得喜欢B款的人数和都可以的人数;得到“都可以”的人数,再计算出它所占的百分比,用360°乘以“都可以”的百分比即可求得所占圆心角的度数;然后补全条形统计图;(2)、用样本中持“喜欢A款”的百分比乘以600估算喜欢A款的有多少人.
试题解析:(1)、12÷20%=60(人)
60×15%=9(人)
60﹣28﹣12﹣9=11(人)
扇形统计图中认为“都可以”的所占圆心角为360×=66度;
图如下:
(2)、600×=280(人)
考点:(1)、条形统计图;(2)、用样本估计总体;(3)、扇形统计图.
2.(1)补全统计表和统计图详见解析;(2)
144;(3)
B当选.
【解析】
试题分析:(1)根据统计图可得A的口试成绩是90,根据统计表可得C的笔试成绩是90分,即可作图;
(2)利用B所占的比例乘以360度即可求解;
(3)首先求得A、B、C的投票得分,然后利用加权平均数公式即可求解.
试题解析:(1)补充图形如下:
竞选人
A
B
C
笔试
85
95
90
口试
90
80
85
;
(2)360°×40%=144°,
故答案为:144°;
(3)A的投票得分是:300×35%=105(分),则A的最后得分是=92.5(分);
B的投票得到是:300×40%=120(分),则B的最后得分是=98(分);
C的投票得分是:300×25%=75(分),则C的最终得分是=84(分).
所以B当选.
考点:条形统计图;统计表;加权平均数.
3.(1)、36°;(2)、答案见解析;(3)、1700人
【解析】
试题分析:(1)、利用C级所在的扇形的圆心角度数=C级的百分比×360°求解即可,(2)、先求出抽样总人数,现求出C级的学生数即可作图.(3)、利用安全知识竞赛中A级和B级的学生数=总人数×(A级的百分比+B级的百分比)求解即可.
试题解析:(1)、C级所在的扇形的圆心角度数为(1﹣49%﹣36%﹣5%)×360°=36°,
(2)、抽样总人数为49÷49%=100人,C级的学生数为100×10%=10人;作图,
(3)、安全知识竞赛中A级和B级的学生数为2000×(49%+36%)=1700人.
考点:(1)、条形统计图;(2)、用样本估计总体;(3)、扇形统计图.
4.(1)、560名;(2)、答案见解析;(3)、4.8万
【解析】
试题分析:(1)、根据扇形统计图专注听讲的百分比与条形统计图中专注听讲的人数,列式计算即可;(2)、用被抽查的学生人数减去主动质疑、独立思考、专注听讲的人数,求出讲解题目的人数,然后补全统计图即可;(3)、用独立思考的学生的百分比乘以16万,进行计算即可得解.
试题解析:(1)、224÷40%=560名;
(2)、讲解题目的学生数为:560﹣84﹣168﹣224=560﹣476=84,补全统计图如图;
(3)、168÷560×16=4.8万,
考点:(1)、条形统计图;(2)、用样本估计总体;(3)、扇形统计图.
5.(1)补全条形统计图详见解析;(2)3;(3)378.
【解析】
试题分析:(1)根据D类垃圾量和所占的百分比即可求得垃圾总数,然后乘以其所占的百分比即可求得每个小组的频数从而补全统计图;
(2)求得C组所占的百分比,即可求得C组的垃圾总量;
(3)首先求得可回收垃圾量,然后求得塑料颗粒料即可.
试题解析:(1)观察统计图知:D类垃圾有5吨,占10%,
垃圾总量为5÷10%=50(吨),
故B类垃圾共有50×30%=15(吨),
如图所示:
(2)∵C组所占的百分比为:1﹣10%﹣30%﹣54%=6%,
∴有害垃圾为:50×6%=3(吨),
故答案为:3;
(3)5000×54%××0.7=378(吨),
答:每月回收的塑料类垃圾可以获得378吨二级原料.
考点:条形统计图;统计表;扇形统计图.
6.(1)120;(2)30°,25;(3)375.
【解析】
试题分析:(1)根据折线统计图可得出本次接受问卷调查的学生总人数是20+60+30+10,再计算即可;(2)用360°乘以“了解”占的百分比即可求出所对应扇形的圆心角的度数,用基本了解的人数除以接受问卷调查的学生总人数即可求出m的值;(3)用该校总人数乘以对足球的了解程度为“基本了解”的人数所占的百分比即可.
试题解析:(1)本次接受问卷调查的学生总人数是20+60+30+10=120(人);
(2)“了解”所对应扇形的圆心角的度数为:360°×=30°;×100%=25%,则m的值是25;
(3)若该校共有学生1500名,则该校学生对足球的了解程度为“基本了解”的人数为:1500×25%=375.
考点:折线统计图;用样本估计总体;扇形统计图.
7.(1)100;(2)6,4,4%;(3)44;(4)768
【解析】
试题分析:(1)由统计表可以得到本次调查的学生数;
(2)由统计图和统计表可以分别求得a、b、c的值;
(3)由统计图和统计表可以求得四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多多少人;
(4)根据统计表可以求得该校学生四月份人均诵读时间在1小时以上的人数.
试题解析:(1)由统计表可得,
本次调查的学生数为:10÷10%=100,
故答案为:100;
(2)由条形统计图可得,a=100﹣60﹣30﹣4=6,
由统计表可得,b=100﹣6﹣30﹣100×50%﹣10=4,c=4÷100=4%,
故答案为:6,4,4%;
(3)由统计表可得,四月份日人均诵读时间在1<x≤1.5范围内的人数有:100×50%=50(人),
由频数分布直方图得,三月份日人均诵读时间在1<x≤1.5范围内的人数有6(人),
故四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多:50﹣4=44(人),
故答案为:44;
(4)由统计表可得,
计该校学生四月份人均诵读时间在1小时以上的人数有:1200×(50%+10%+4%)=768(人),
即计该校学生四月份人均诵读时间在1小时以上的人数有768人.
考点:1、频数分布直方图,2、频数分布表,3、用样本估计总体
8.(1)72°,这天载客量的中位数在B组;(2)38人;(3)5路公共汽车一个月的总载客量约为5.7×104人.
【解析】
试题分析:(1)利用360°乘以A组所占比例即可;(2)首先计算出各组的组中值,然后再利用加权平均数公式计算平均数;(3)利用平均每班的载客量×天数×次数可得一个月的总载客量.
试题解析:(1)A组对应扇形圆心角度数为:360°×=72°;
这天载客量的中位数在B组;
(2)各组组中值为:A:
=10,B:=30;C:
=50;D:
=70;
==38(人),
答:这天5路公共汽车平均每班的载客量是38人;
(3)可以估计,一个月的总载客量约为38×50×30=57000=5.7×104(人),
答:5路公共汽车一个月的总载客量约为5.7×104人.
考点:频数(率)分布直方图;扇形统计图;中位数.
1.自1939年创办以来,重庆育才中学一直坚守文化底线,不断挑战自我极限,在沧桑文化中愈加根深叶茂.在今年,即将推出的本部改造计划不仅是文化审美层面的颠覆尝试,也是学校发展的巨大工程,其中三种style的民国大门各具特色,A磅礴大气,B清爽简约,C典雅古朴款,为调查民意学校让教职工进行投票呈现了四种结果,喜欢A款、喜欢B款、喜欢C款、都可以,现调查结果如下:
(1)如图,喜欢C款的占20%,喜欢B款的占15%,则调查总人数为,扇形统计图中认为“都可以”的所占圆心角为度;根据题中信息补全条形统计图.
(2)我们学校共有600名教职工,请根据上图估算喜欢A款的有多少人?
2.A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:
竞选人
A
B
C
笔试
85
95
90
口试
80
85
(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角是
度.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
3.2014年3月28日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列两幅统计图(说明:A级:90~100分;B级:75~89分;C级:60~74分;D级:60分以下).请结合图中提供的信息,解答下列问题:
(1)求扇形统计图2中C级所在的扇形的圆心角度数;
(2)请把条形统计图1补充完整并写出计算过程;
(3)若该校共有2000名学生,请你估计安全知识竞赛中A级和B级的学生一共有多少人?
4.林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了
名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
5.垃圾的分类处理与回收利用,可以减少污染,节省资源,生活垃圾一般按如图所示A、B、C、D四种分类方法回收处理,某城市环保部门为了提高宣传实效,抽样调查、统计了部分居民小区一段时间内生活垃圾的分类处理情况,并将调查统计结果绘制成如下两幅不完整的统计图表:
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共
吨;
(3)调查发现,在可回收物中塑料类垃圾占,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
6.在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
(1)本次接受问卷调查的学生总人数是
;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为
,m的值为
;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.
7.某校1200名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
根据以上信息,解答下列问题:
(1)本次调查的学生数为
人;
(2)图表中的a、b、c的值分别为
,
,
;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多
人;
(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.
四月日人均诵读时间的统计表
日人均诵读时间x/h
人数
百分比
0≤x≤0.5
6
0.5<x≤1
30
1<x≤1.5
50%
1.5<x≤2
10
10%
2<x≤2.5
b
c
三月日人均诵读时间的频数分布直方图
8.根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图:
(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
参考答案
1.(1)、60人;66°;图形见解析;(2)、280人.
【解析】
试题分析:(1)、观察统计图,利用喜欢C款的人数除以它所占的百分比即可得到调查的总人数,进一步求得喜欢B款的人数和都可以的人数;得到“都可以”的人数,再计算出它所占的百分比,用360°乘以“都可以”的百分比即可求得所占圆心角的度数;然后补全条形统计图;(2)、用样本中持“喜欢A款”的百分比乘以600估算喜欢A款的有多少人.
试题解析:(1)、12÷20%=60(人)
60×15%=9(人)
60﹣28﹣12﹣9=11(人)
扇形统计图中认为“都可以”的所占圆心角为360×=66度;
图如下:
(2)、600×=280(人)
考点:(1)、条形统计图;(2)、用样本估计总体;(3)、扇形统计图.
2.(1)补全统计表和统计图详见解析;(2)
144;(3)
B当选.
【解析】
试题分析:(1)根据统计图可得A的口试成绩是90,根据统计表可得C的笔试成绩是90分,即可作图;
(2)利用B所占的比例乘以360度即可求解;
(3)首先求得A、B、C的投票得分,然后利用加权平均数公式即可求解.
试题解析:(1)补充图形如下:
竞选人
A
B
C
笔试
85
95
90
口试
90
80
85
;
(2)360°×40%=144°,
故答案为:144°;
(3)A的投票得分是:300×35%=105(分),则A的最后得分是=92.5(分);
B的投票得到是:300×40%=120(分),则B的最后得分是=98(分);
C的投票得分是:300×25%=75(分),则C的最终得分是=84(分).
所以B当选.
考点:条形统计图;统计表;加权平均数.
3.(1)、36°;(2)、答案见解析;(3)、1700人
【解析】
试题分析:(1)、利用C级所在的扇形的圆心角度数=C级的百分比×360°求解即可,(2)、先求出抽样总人数,现求出C级的学生数即可作图.(3)、利用安全知识竞赛中A级和B级的学生数=总人数×(A级的百分比+B级的百分比)求解即可.
试题解析:(1)、C级所在的扇形的圆心角度数为(1﹣49%﹣36%﹣5%)×360°=36°,
(2)、抽样总人数为49÷49%=100人,C级的学生数为100×10%=10人;作图,
(3)、安全知识竞赛中A级和B级的学生数为2000×(49%+36%)=1700人.
考点:(1)、条形统计图;(2)、用样本估计总体;(3)、扇形统计图.
4.(1)、560名;(2)、答案见解析;(3)、4.8万
【解析】
试题分析:(1)、根据扇形统计图专注听讲的百分比与条形统计图中专注听讲的人数,列式计算即可;(2)、用被抽查的学生人数减去主动质疑、独立思考、专注听讲的人数,求出讲解题目的人数,然后补全统计图即可;(3)、用独立思考的学生的百分比乘以16万,进行计算即可得解.
试题解析:(1)、224÷40%=560名;
(2)、讲解题目的学生数为:560﹣84﹣168﹣224=560﹣476=84,补全统计图如图;
(3)、168÷560×16=4.8万,
考点:(1)、条形统计图;(2)、用样本估计总体;(3)、扇形统计图.
5.(1)补全条形统计图详见解析;(2)3;(3)378.
【解析】
试题分析:(1)根据D类垃圾量和所占的百分比即可求得垃圾总数,然后乘以其所占的百分比即可求得每个小组的频数从而补全统计图;
(2)求得C组所占的百分比,即可求得C组的垃圾总量;
(3)首先求得可回收垃圾量,然后求得塑料颗粒料即可.
试题解析:(1)观察统计图知:D类垃圾有5吨,占10%,
垃圾总量为5÷10%=50(吨),
故B类垃圾共有50×30%=15(吨),
如图所示:
(2)∵C组所占的百分比为:1﹣10%﹣30%﹣54%=6%,
∴有害垃圾为:50×6%=3(吨),
故答案为:3;
(3)5000×54%××0.7=378(吨),
答:每月回收的塑料类垃圾可以获得378吨二级原料.
考点:条形统计图;统计表;扇形统计图.
6.(1)120;(2)30°,25;(3)375.
【解析】
试题分析:(1)根据折线统计图可得出本次接受问卷调查的学生总人数是20+60+30+10,再计算即可;(2)用360°乘以“了解”占的百分比即可求出所对应扇形的圆心角的度数,用基本了解的人数除以接受问卷调查的学生总人数即可求出m的值;(3)用该校总人数乘以对足球的了解程度为“基本了解”的人数所占的百分比即可.
试题解析:(1)本次接受问卷调查的学生总人数是20+60+30+10=120(人);
(2)“了解”所对应扇形的圆心角的度数为:360°×=30°;×100%=25%,则m的值是25;
(3)若该校共有学生1500名,则该校学生对足球的了解程度为“基本了解”的人数为:1500×25%=375.
考点:折线统计图;用样本估计总体;扇形统计图.
7.(1)100;(2)6,4,4%;(3)44;(4)768
【解析】
试题分析:(1)由统计表可以得到本次调查的学生数;
(2)由统计图和统计表可以分别求得a、b、c的值;
(3)由统计图和统计表可以求得四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多多少人;
(4)根据统计表可以求得该校学生四月份人均诵读时间在1小时以上的人数.
试题解析:(1)由统计表可得,
本次调查的学生数为:10÷10%=100,
故答案为:100;
(2)由条形统计图可得,a=100﹣60﹣30﹣4=6,
由统计表可得,b=100﹣6﹣30﹣100×50%﹣10=4,c=4÷100=4%,
故答案为:6,4,4%;
(3)由统计表可得,四月份日人均诵读时间在1<x≤1.5范围内的人数有:100×50%=50(人),
由频数分布直方图得,三月份日人均诵读时间在1<x≤1.5范围内的人数有6(人),
故四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多:50﹣4=44(人),
故答案为:44;
(4)由统计表可得,
计该校学生四月份人均诵读时间在1小时以上的人数有:1200×(50%+10%+4%)=768(人),
即计该校学生四月份人均诵读时间在1小时以上的人数有768人.
考点:1、频数分布直方图,2、频数分布表,3、用样本估计总体
8.(1)72°,这天载客量的中位数在B组;(2)38人;(3)5路公共汽车一个月的总载客量约为5.7×104人.
【解析】
试题分析:(1)利用360°乘以A组所占比例即可;(2)首先计算出各组的组中值,然后再利用加权平均数公式计算平均数;(3)利用平均每班的载客量×天数×次数可得一个月的总载客量.
试题解析:(1)A组对应扇形圆心角度数为:360°×=72°;
这天载客量的中位数在B组;
(2)各组组中值为:A:
=10,B:=30;C:
=50;D:
=70;
==38(人),
答:这天5路公共汽车平均每班的载客量是38人;
(3)可以估计,一个月的总载客量约为38×50×30=57000=5.7×104(人),
答:5路公共汽车一个月的总载客量约为5.7×104人.
考点:频数(率)分布直方图;扇形统计图;中位数.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
