19.2.1正比例函数 课件
图片预览






文档简介
课件18张PPT。19.2.1正比例函数历史使人聪明,诗歌使人机智,数学使人精细。
--------培根数学是最宝贵的研究精神之一。
------华罗庚鸟类研究者在芬兰给一只燕鸥(候鸟)套上标志环;大约128天后,人们在25600千米外的澳大利亚发现了它.(1)这只燕鸥大约平均每天飞行多少千米?
(2) 这只燕鸥的行程y(单位:千米)与飞行时间x(单位:天)之间有什么关系?
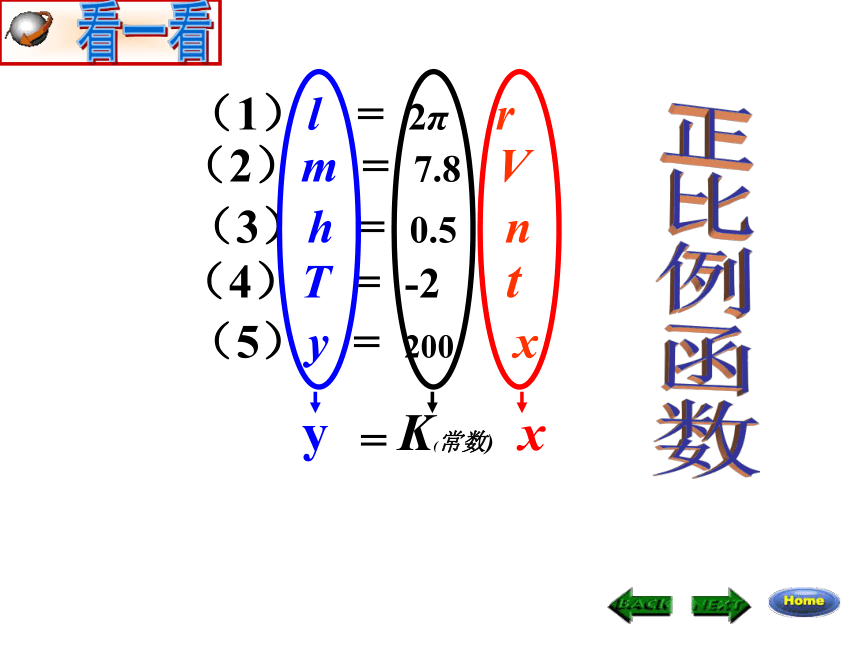
解:25600÷128=200(km)y=200x (0≤x≤128)(3)这只燕鸥飞行1个月(一个月按30天计算)的行程大约是多少千米?情景引入当x=30时,y=200×30=6000(千米)写出下列问题中的函数关系式(2)铁的密度为7.8g/cm3 ,铁块的质量m(单位:g)随它的体积v(单位:cm3)大小变化而变化;(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度 h随这些练习本的本数n的变化而变化;(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化.做一做(2)m = 7.8 V(3)h = 0.5 n(4)T = -2 t(5)y = 200 x(1)l = 2π ryK(常数)x=看一看正比例函数下列函数中哪些是正比例函数?(2)y = x+2(1)y =2x(5)y=x2+1 是是不是不是不是不是小试牛刀例1、
(1)如果y=3x+k-4,是y关于x的正比例函数,则
k=_________.
≠14思维拓展(1)若 是正比例函数,则k= 。
K=3-1(3)如果 是y关于x的正比例函数,求k的值(2)如果y=(k-1)x,是y关于x的正比例函数,则K_________(2)若 是正比例函数,则m= .2(二)正比例函数的图象与性质画出下列函数的图像
(1) y=2x (2)
(3)y=-2x (4)图象:正比例函数y=kx(k是常数,k≠0)的图象是一条经过 的直线,我们称它为直线y=kx.
性质:当k>0时,直线y=kx经过第 象限,从左向右 ,y随着x的增大而 ;
当k<0时,直线y=kx经过第 象限,从左向右 ,y随着x的增大而 .总结三、一原点上升增大二、四下降减小知道正比例函数是一条直线,那么画正比例函数图像有无简便方法?思考解:选取两点(0,0) , (1,3)例2:画函数 y = 3x 的图象y=3x过这两点画直线,画一画:画出下列函数的图像
(1)y=-2x
(2)二、四0-3减小3. 函数y=-3x的图象在第 象限内,经过点2. 正比例函数y=(3-k) x,如果随着x的增大y反而减
小,则k的取值范围是 ______.k>34. 函数y= x的图象在第 象限内,经过点(0, )与点(1, ),y随x的增大而 .(0, )与点(1, ),y随x的增大而 .三、一0增大勇往直前1 (2015·北海)正比例函数y=kx的图象如图所示,
则k的取值范围是( )
A.k>0 B.k<0 C.k>1 D.k<1A5.正比例函数y=kx的图象如图所示,则这个函数的解析式是 。 1-2y=-2x1、〈珠海〉已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).>能力提升方法总结:方法一是利用求值比较法;方法二是利用数形结合思想,用“形”上的 点的位置来比较“数”的大小;方法三是利用函数的增减性来比较大小.2、 P1(x1,y1),P2(x2,y2)是正比例函数y= 的图
象上的两点,则下列判断正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1>y2
D.当x1<x2时,y1<y2,C能力提升你今天学习了什么?
有什么收获?学无止境迎难而上解析式y = kx (k>0)y = kx (k<0)图 象图象位置函数变化 图象:正比例函数y= kx (k≠0) 的图象是经过____和点_____的一条直线。第___ 象限第___ 象限y随着x
的增大
而____y随着x
的增大
而____课堂小结定义:形如 的函数,叫正比例函数。必做题:
课本第98页1、2 题.选做题:推荐作业1 函数y=(k2-4)x+(k+1)是正比例函数,且y随x的增大而减小.求函数的解析式.
2 已知y与x成正比例,且当x=3时,y=-9.
(1)求y与x之间的函数关系式;
(2)画出函数图象;
(3)点P(-1,3)和Q(-6,3)是否在此函数图象上?
--------培根数学是最宝贵的研究精神之一。
------华罗庚鸟类研究者在芬兰给一只燕鸥(候鸟)套上标志环;大约128天后,人们在25600千米外的澳大利亚发现了它.(1)这只燕鸥大约平均每天飞行多少千米?
(2) 这只燕鸥的行程y(单位:千米)与飞行时间x(单位:天)之间有什么关系?
解:25600÷128=200(km)y=200x (0≤x≤128)(3)这只燕鸥飞行1个月(一个月按30天计算)的行程大约是多少千米?情景引入当x=30时,y=200×30=6000(千米)写出下列问题中的函数关系式(2)铁的密度为7.8g/cm3 ,铁块的质量m(单位:g)随它的体积v(单位:cm3)大小变化而变化;(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度 h随这些练习本的本数n的变化而变化;(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化.做一做(2)m = 7.8 V(3)h = 0.5 n(4)T = -2 t(5)y = 200 x(1)l = 2π ryK(常数)x=看一看正比例函数下列函数中哪些是正比例函数?(2)y = x+2(1)y =2x(5)y=x2+1 是是不是不是不是不是小试牛刀例1、
(1)如果y=3x+k-4,是y关于x的正比例函数,则
k=_________.
≠14思维拓展(1)若 是正比例函数,则k= 。
K=3-1(3)如果 是y关于x的正比例函数,求k的值(2)如果y=(k-1)x,是y关于x的正比例函数,则K_________(2)若 是正比例函数,则m= .2(二)正比例函数的图象与性质画出下列函数的图像
(1) y=2x (2)
(3)y=-2x (4)图象:正比例函数y=kx(k是常数,k≠0)的图象是一条经过 的直线,我们称它为直线y=kx.
性质:当k>0时,直线y=kx经过第 象限,从左向右 ,y随着x的增大而 ;
当k<0时,直线y=kx经过第 象限,从左向右 ,y随着x的增大而 .总结三、一原点上升增大二、四下降减小知道正比例函数是一条直线,那么画正比例函数图像有无简便方法?思考解:选取两点(0,0) , (1,3)例2:画函数 y = 3x 的图象y=3x过这两点画直线,画一画:画出下列函数的图像
(1)y=-2x
(2)二、四0-3减小3. 函数y=-3x的图象在第 象限内,经过点2. 正比例函数y=(3-k) x,如果随着x的增大y反而减
小,则k的取值范围是 ______.k>34. 函数y= x的图象在第 象限内,经过点(0, )与点(1, ),y随x的增大而 .(0, )与点(1, ),y随x的增大而 .三、一0增大勇往直前1 (2015·北海)正比例函数y=kx的图象如图所示,
则k的取值范围是( )
A.k>0 B.k<0 C.k>1 D.k<1A5.正比例函数y=kx的图象如图所示,则这个函数的解析式是 。 1-2y=-2x1、〈珠海〉已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).>能力提升方法总结:方法一是利用求值比较法;方法二是利用数形结合思想,用“形”上的 点的位置来比较“数”的大小;方法三是利用函数的增减性来比较大小.2、 P1(x1,y1),P2(x2,y2)是正比例函数y= 的图
象上的两点,则下列判断正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1>y2
D.当x1<x2时,y1<y2,C能力提升你今天学习了什么?
有什么收获?学无止境迎难而上解析式y = kx (k>0)y = kx (k<0)图 象图象位置函数变化 图象:正比例函数y= kx (k≠0) 的图象是经过____和点_____的一条直线。第___ 象限第___ 象限y随着x
的增大
而____y随着x
的增大
而____课堂小结定义:形如 的函数,叫正比例函数。必做题:
课本第98页1、2 题.选做题:推荐作业1 函数y=(k2-4)x+(k+1)是正比例函数,且y随x的增大而减小.求函数的解析式.
2 已知y与x成正比例,且当x=3时,y=-9.
(1)求y与x之间的函数关系式;
(2)画出函数图象;
(3)点P(-1,3)和Q(-6,3)是否在此函数图象上?
